人教版八年级上册13.3.2.2含30°角的直角三角形的性质 教学设计(表格式)
文档属性
| 名称 | 人教版八年级上册13.3.2.2含30°角的直角三角形的性质 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 189.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 初中数学 年级 八年级 学期 秋季
课题 等边三角形(第二课时)
教科书 书 名:数学教材 出版社:人民教育出版社 出版日期:2013年6月
教学目标
1. 探索并理解含30°角的直角三角形的性质.培养学生用规范的几何语言进行表达的习惯和能力。 2. 理解含30°角的直角三角形的性质,并会应用它进行有关的证明和计算。
教学内容
教学重点: 1. 探索并理解含30°角的直角三角形的性质。 2. 含30°角的直角三角形的性质的应用。 教学难点: 1. 含30°角的直角三角形性质的探索与证明。
教学过程
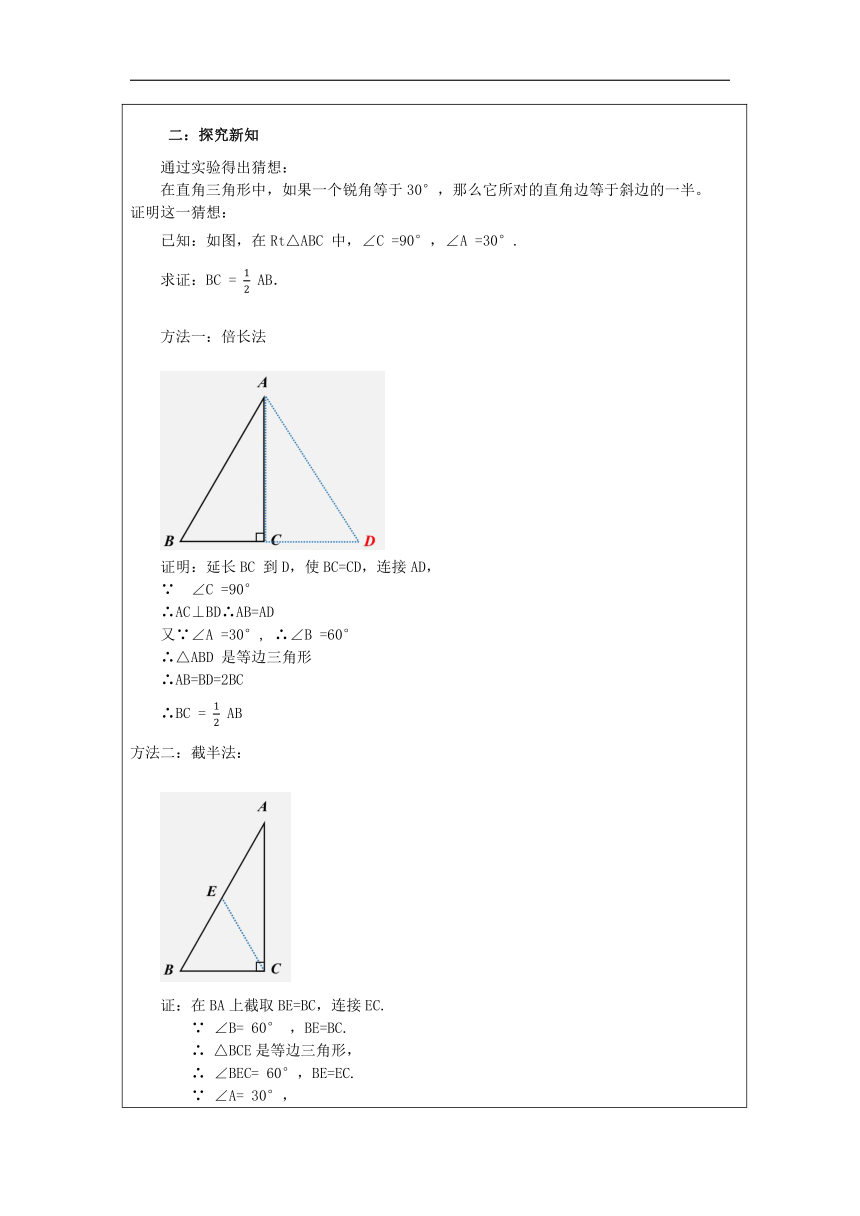
一:问题探究 让学生自己动手通过两个数学小实验探究含30°角的直角三角形性质 问题1 将一张等边三角形纸片,沿一边上的高对折,能产生什么样的特殊图形? 问题2 如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗? 设计意图:提出问题.创设情境,导入新课. 二:探究新知 通过实验得出猜想: 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。 证明这一猜想: 已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB. 方法一:倍长法 证明:延长BC 到D,使BC=CD,连接AD, ∵ ∠C =90° ∴AC⊥BD∴AB=AD 又∵∠A =30°, ∴∠B =60° ∴△ABD 是等边三角形 ∴AB=BD=2BC ∴BC = AB 方法二:截半法: 证:在BA上截取BE=BC,连接EC. ∵ ∠B= 60° ,BE=BC. ∴ △BCE是等边三角形, ∴ ∠BEC= 60°,BE=EC. ∵ ∠A= 30°, ∴ ∠ECA=∠BEC-∠A=60°-30° = 30° ∴ AE=EC, ∴ AE=BE=BC, ∴ AB=AE+BE=2BC. ∴BC = AB 于是我们得到: 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 用几何语言表示: ∵在Rt△ABC中,∠C=90°,∠A=30°, ∴BC=AB. 设计意图:学生经历折叠等边三角形纸片和拼摆三角板的活动,发现结论,引导学生意识到,通过实际操作探索出来的结论,还需要给予证明,培养学生的语言转换能力,增强理性认识,体验性质的正确性,提高演绎推理的能力. 三:典例解析 例1 如图,在Rt△ABC中,∠ACB=90°,∠B=30°, CD是斜边AB上的高,AD=3cm,则AB的长度是( ) A.3cm B.6cm C.9cm D.12cm 解析:在Rt△ABC中, ∵CD是斜边AB上的高, ∴∠ADC=90°,∴∠ACD=∠B=30°. 在Rt△ACD中,AC=2AD=6cm, 在Rt△ABC中,AB=2AC=12cm. ∴AB的长度是12cm.故选D. 注意:运用含30°角的直角三角形的性质求线段长时,要分清线段所在的直角三角形. 例2.如图,已知∠AOB=60°,点P在边OA上, OP=12,点M、N在边OB上,PM=PN,若MN=5, 则OM的长度为 . 解析:作PC⊥OB∵PM=PN,∴MC=NC=1/2MN=2.5, 又∵∠AOB=60°∴∠OPC=30°. 在Rt△OPC中,OP=2OC=6, OM=OC-MC=3.5∴OM的长度是3.5. 方法总结:含30°角的直角三角形与等腰三角形的综合运用时,关键是寻找或作辅助线构造含30°角的直角三角形. 四:巩固提升 如图,已知△ABC是等边三角形,D、E 分别为BC、 AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q, 求证:BP=2PQ. 证明:∵△ABC为等边三角形, ∴ AC=BC=AB ,∠C=∠BAC=60° ∵CD=AE, ∴△ADC≌△BEA. ∴∠CAD=∠ABE. ∵∠BAP+∠CAD=60°, ∴∠ABE+∠BAP=60°. ∴∠BPQ=60°. 又∵ BQ⊥AD, ∴∠BQP=90°, ∴∠PBQ=30°, ∴BP=2PQ. 方法总结:含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据,如果问题中出现探究线段倍分关系的结论时,要联想此性质. 五:梳理小结
课程基本信息
学科 初中数学 年级 八年级 学期 秋季
课题 等边三角形(第二课时)
教科书 书 名:数学教材 出版社:人民教育出版社 出版日期:2013年6月
教学目标
1. 探索并理解含30°角的直角三角形的性质.培养学生用规范的几何语言进行表达的习惯和能力。 2. 理解含30°角的直角三角形的性质,并会应用它进行有关的证明和计算。
教学内容
教学重点: 1. 探索并理解含30°角的直角三角形的性质。 2. 含30°角的直角三角形的性质的应用。 教学难点: 1. 含30°角的直角三角形性质的探索与证明。
教学过程
一:问题探究 让学生自己动手通过两个数学小实验探究含30°角的直角三角形性质 问题1 将一张等边三角形纸片,沿一边上的高对折,能产生什么样的特殊图形? 问题2 如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗? 设计意图:提出问题.创设情境,导入新课. 二:探究新知 通过实验得出猜想: 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。 证明这一猜想: 已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB. 方法一:倍长法 证明:延长BC 到D,使BC=CD,连接AD, ∵ ∠C =90° ∴AC⊥BD∴AB=AD 又∵∠A =30°, ∴∠B =60° ∴△ABD 是等边三角形 ∴AB=BD=2BC ∴BC = AB 方法二:截半法: 证:在BA上截取BE=BC,连接EC. ∵ ∠B= 60° ,BE=BC. ∴ △BCE是等边三角形, ∴ ∠BEC= 60°,BE=EC. ∵ ∠A= 30°, ∴ ∠ECA=∠BEC-∠A=60°-30° = 30° ∴ AE=EC, ∴ AE=BE=BC, ∴ AB=AE+BE=2BC. ∴BC = AB 于是我们得到: 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 用几何语言表示: ∵在Rt△ABC中,∠C=90°,∠A=30°, ∴BC=AB. 设计意图:学生经历折叠等边三角形纸片和拼摆三角板的活动,发现结论,引导学生意识到,通过实际操作探索出来的结论,还需要给予证明,培养学生的语言转换能力,增强理性认识,体验性质的正确性,提高演绎推理的能力. 三:典例解析 例1 如图,在Rt△ABC中,∠ACB=90°,∠B=30°, CD是斜边AB上的高,AD=3cm,则AB的长度是( ) A.3cm B.6cm C.9cm D.12cm 解析:在Rt△ABC中, ∵CD是斜边AB上的高, ∴∠ADC=90°,∴∠ACD=∠B=30°. 在Rt△ACD中,AC=2AD=6cm, 在Rt△ABC中,AB=2AC=12cm. ∴AB的长度是12cm.故选D. 注意:运用含30°角的直角三角形的性质求线段长时,要分清线段所在的直角三角形. 例2.如图,已知∠AOB=60°,点P在边OA上, OP=12,点M、N在边OB上,PM=PN,若MN=5, 则OM的长度为 . 解析:作PC⊥OB∵PM=PN,∴MC=NC=1/2MN=2.5, 又∵∠AOB=60°∴∠OPC=30°. 在Rt△OPC中,OP=2OC=6, OM=OC-MC=3.5∴OM的长度是3.5. 方法总结:含30°角的直角三角形与等腰三角形的综合运用时,关键是寻找或作辅助线构造含30°角的直角三角形. 四:巩固提升 如图,已知△ABC是等边三角形,D、E 分别为BC、 AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q, 求证:BP=2PQ. 证明:∵△ABC为等边三角形, ∴ AC=BC=AB ,∠C=∠BAC=60° ∵CD=AE, ∴△ADC≌△BEA. ∴∠CAD=∠ABE. ∵∠BAP+∠CAD=60°, ∴∠ABE+∠BAP=60°. ∴∠BPQ=60°. 又∵ BQ⊥AD, ∴∠BQP=90°, ∴∠PBQ=30°, ∴BP=2PQ. 方法总结:含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据,如果问题中出现探究线段倍分关系的结论时,要联想此性质. 五:梳理小结
