数学:4.2.1《函数模型及其应用》课件(北师大版必修1)
文档属性
| 名称 | 数学:4.2.1《函数模型及其应用》课件(北师大版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 173.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 05:40:00 | ||
图片预览



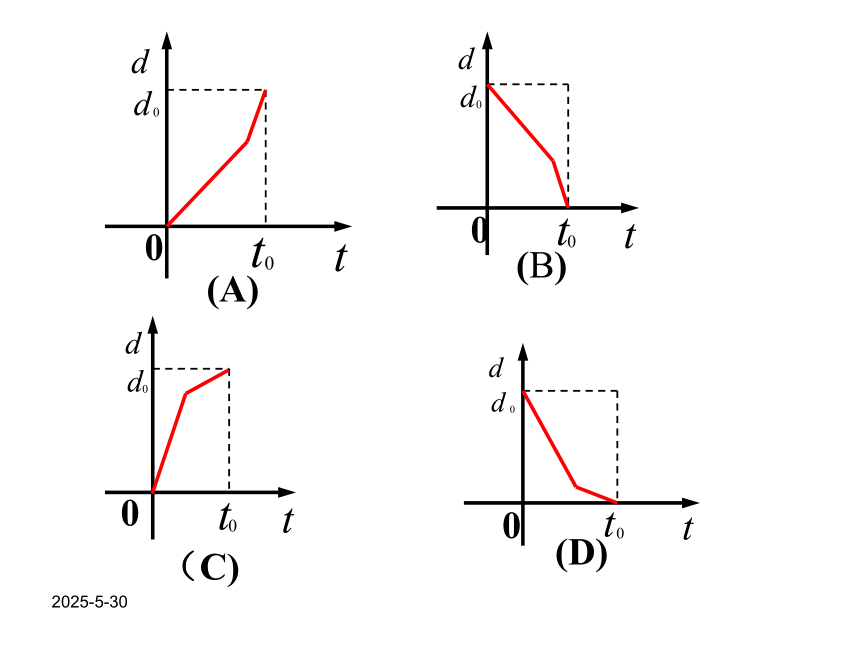
文档简介
课件13张PPT。4.2.1函数模型及其应用2019-3-131.一次函数的解析式为__________________ , 其图像是一条____线,
当________时,一次函数在 上为增函数,
当_______时, 一次函数在 上为减函数。2.二次函数的解析式为_______________________, 其图像是一条
________线,当______时,函数有最小值为___________,当______
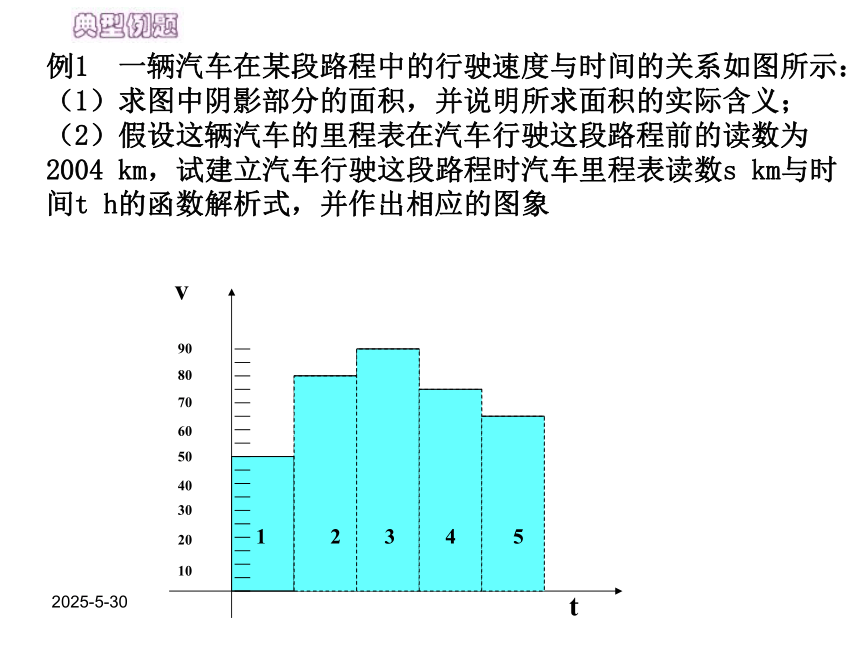
时,函数有最大值为____________。抛物直2019-3-13问题某学生早上起床太晚,为避免迟到,不得不跑步到教室,但由于平时不注意锻炼身体,结果跑了一段就累了,不得不走完余下的路程。如果用纵轴表示家到教室的距离,横轴表示出发后的时间,则下列四个图象比较符合此人走法的是( )2019-3-130(C)2019-3-1312345例1 一辆汽车在某段路程中的行驶速度与时间的关系如图所示:
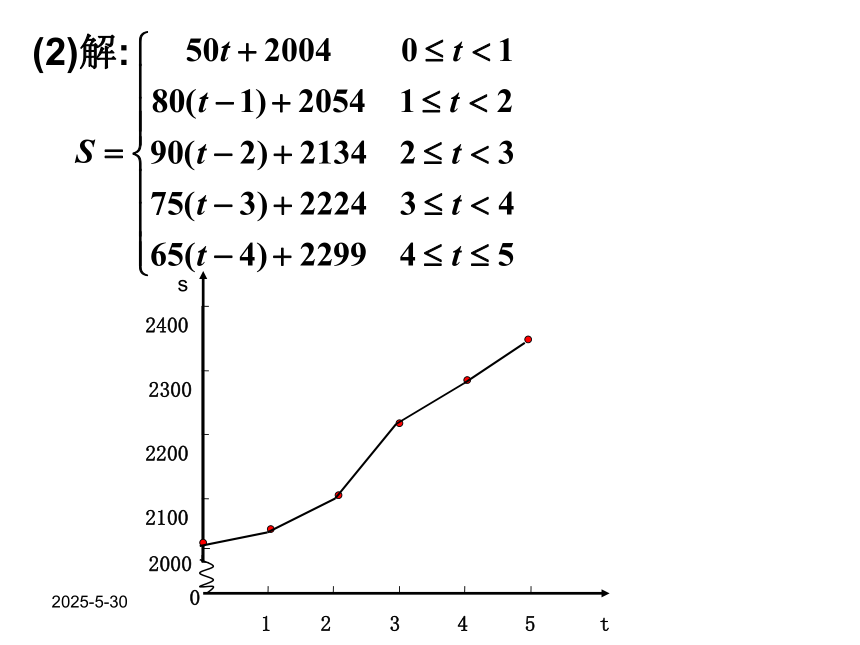
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立汽车行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象2019-3-132019-3-13总结解应用题的策略:一般思路可表示如下:
2019-3-13因此,解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.2019-3-13例2 人口增长模型: 其中t表示经过的时间, y0表示t=0时的人口数,r表示人口的年平均增长率. 下表是1950年~1959年我国的人口数据资料:(2)如果按表上表的增长趋势,大约在哪一年我国的人口达到13亿?(1)如果以各年人中增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;2019-3-13于是,1951~1959年期间,我国人口的年平均增长率为2019-3-13 由上图可以看出,所得模型与1950~1959年的实际人中数据基本吻合.2019-3-13注意点:
1.在引入自变量建立目标函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求.
2.在实际问题向数学问题的转化过程中,要充分使用数学语言,如引入字母,列表,画图等使实际问题数学符号化.
3.对于建立的各种数学模型,要能够模型识别,充分利用数学方法加以解决,并能积累一定数量的典型的函数模型,这是顺利解决实际问题的重要资本.2019-3-13小结 本节内容主要是运用所学的函数知识去解
决实际问题,要求学生掌握函数应用的基本
方法和步骤.函数的应用问题是高考中的热
点内容,必须下功夫练好基本功.本节涉及
的函数模型有:一次函数、二次函数、分段
函数及较简单的指数函数和对数函数.其
中,最重要的是二次函数模型.
2019-3-13
当________时,一次函数在 上为增函数,
当_______时, 一次函数在 上为减函数。2.二次函数的解析式为_______________________, 其图像是一条
________线,当______时,函数有最小值为___________,当______
时,函数有最大值为____________。抛物直2019-3-13问题某学生早上起床太晚,为避免迟到,不得不跑步到教室,但由于平时不注意锻炼身体,结果跑了一段就累了,不得不走完余下的路程。如果用纵轴表示家到教室的距离,横轴表示出发后的时间,则下列四个图象比较符合此人走法的是( )2019-3-130(C)2019-3-1312345例1 一辆汽车在某段路程中的行驶速度与时间的关系如图所示:
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立汽车行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象2019-3-132019-3-13总结解应用题的策略:一般思路可表示如下:
2019-3-13因此,解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.2019-3-13例2 人口增长模型: 其中t表示经过的时间, y0表示t=0时的人口数,r表示人口的年平均增长率. 下表是1950年~1959年我国的人口数据资料:(2)如果按表上表的增长趋势,大约在哪一年我国的人口达到13亿?(1)如果以各年人中增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;2019-3-13于是,1951~1959年期间,我国人口的年平均增长率为2019-3-13 由上图可以看出,所得模型与1950~1959年的实际人中数据基本吻合.2019-3-13注意点:
1.在引入自变量建立目标函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求.
2.在实际问题向数学问题的转化过程中,要充分使用数学语言,如引入字母,列表,画图等使实际问题数学符号化.
3.对于建立的各种数学模型,要能够模型识别,充分利用数学方法加以解决,并能积累一定数量的典型的函数模型,这是顺利解决实际问题的重要资本.2019-3-13小结 本节内容主要是运用所学的函数知识去解
决实际问题,要求学生掌握函数应用的基本
方法和步骤.函数的应用问题是高考中的热
点内容,必须下功夫练好基本功.本节涉及
的函数模型有:一次函数、二次函数、分段
函数及较简单的指数函数和对数函数.其
中,最重要的是二次函数模型.
2019-3-13
