第3单元 圆柱与圆锥(同步练习)(含解析)人教版六年级下册数学
文档属性
| 名称 | 第3单元 圆柱与圆锥(同步练习)(含解析)人教版六年级下册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 114.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 20:26:49 | ||
图片预览



文档简介
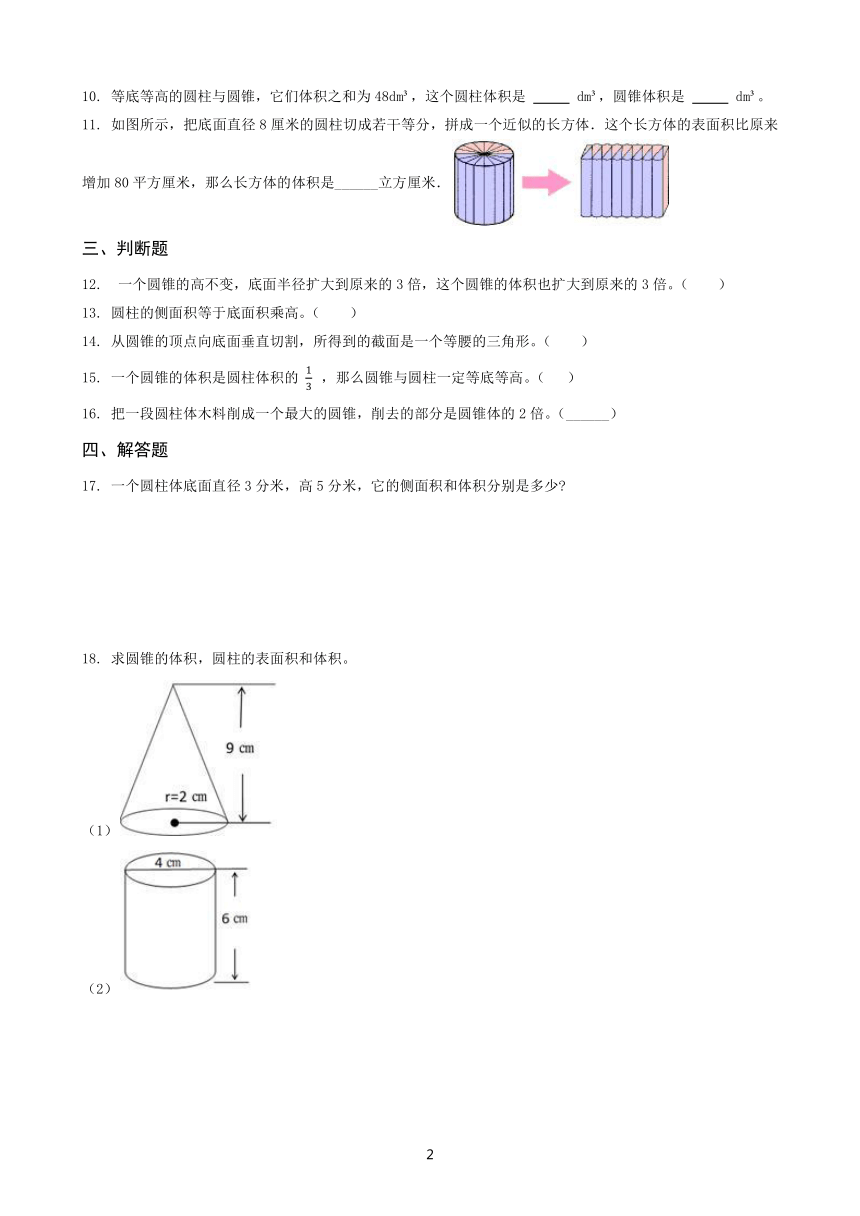
第3单元 圆柱与圆锥
一、单项选择题
1. 圆柱的底面半径和高都扩大3倍,它的体积将扩大( )倍。
A. 3 B. 6 C. 9 D. 27
2. 把一个圆柱削成一个最大的圆锥,削去部分的体积是原体积的( )。
A. B. C.
3. 等底的圆柱和圆锥,圆锥的高是圆柱的3倍,那么它们的体积( )。
A. 圆柱小于圆锥 B. 相等 C. 圆柱大于圆锥
4. 下面的平面图形分别绕虚线旋转一周会形成圆柱的是( ).
A. B. C. D.
5. 小杰做了一个圆柱形容器和几个圆锥形容器,大小如下图所示(单位:cm),将圆柱内的水倒入( )圆锥内,正好倒满。
A. B. C.
6. 如图,用36L的水刚好把这个容器装满。如果水深2.5dm,则容器里有( )L的水。(容器的厚度忽略不计)
A. 18 B. 24 C. 27 D. 30
二、填空题
7. 一个圆柱的侧面展开得到一个长方形,长方形的长是6.28厘米,宽是3厘米,这个圆柱体的侧面积是 平方厘米,表面积是 平方厘米.
8. 一个圆柱的底面直径是8厘米,它的侧面展开正好是一个正方形,这个圆柱的高是 厘米。
9. 将一张长30厘米,宽18厘米的长方形白纸卷成一个圆柱,这个圆柱的侧面积是 平方厘米。
10. 等底等高的圆柱与圆锥,它们体积之和为48dm ,这个圆柱体积是 dm ,圆锥体积是 dm 。
11. 如图所示,把底面直径8厘米的圆柱切成若干等分,拼成一个近似的长方体.这个长方体的表面积比原来增加80平方厘米,那么长方体的体积是______立方厘米.
三、判断题
12. 一个圆锥的高不变,底面半径扩大到原来的3倍,这个圆锥的体积也扩大到原来的3倍。( )
13. 圆柱的侧面积等于底面积乘高。( )
14. 从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形。( )
15. 一个圆锥的体积是圆柱体积的 ,那么圆锥与圆柱一定等底等高。( )
16. 把一段圆柱体木料削成一个最大的圆锥,削去的部分是圆锥体的2倍。(______)
四、解答题
17. 一个圆柱体底面直径3分米,高5分米,它的侧面积和体积分别是多少
18. 求圆锥的体积,圆柱的表面积和体积。
(1)
(2)
19. 一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示。它的容积为26.4 cm 。瓶子正放时,瓶内药水液面高6 cm,瓶子倒放时,空余部分高2 cm,则瓶内药水的体积是多少立方厘米?
20. 一个圆锥形沙堆,底面积是28.26平方米,高是2.5米.用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
参考答案
一、单项选择题
1. 【答案】D
【解析】设原来圆柱的底面半径和高均为1,则有
π×32×3÷(π×12×1)
=27π÷π
=27
所以圆柱的底面半径和高都扩大3倍,它的体积将扩大27倍。
故答案为:D。
2. 【答案】C
【解析】设圆柱的体积是1,则
(1-)÷1
=÷1
=
所以削去部分的体积是原体积的。
故答案为:C。
3. 【答案】B
【解析】解:假设底面积都是S,圆柱的高是h,则圆锥的高是3h;圆柱的体积:Sh;圆锥的体积:S×3h×=Sh;体积相等.
故答案为:B
4. 【答案】C
【解析】解:C项中的图形绕虚线旋转一周会形成圆柱。
故答案为:C。
5. 【答案】A
【解析】解:3.14×(10÷2)2×6=3.14×150(cm3);
A:3.14×(10÷2)2×18×=3.14×150(cm3),正好倒满;
B:3.14×(12÷2)2×18×=3.14×216,不能正好倒满;
C:3.14×(10÷2)2×15×=3.14×125,不能正好倒满。
6. 【答案】C
【解析】这个容器有圆柱和圆锥两部分组成,且圆柱和圆锥的底面积相等,设圆柱和圆锥的底面积是x平方分米,根据圆柱容积+圆锥容积=36,列出方程,求出底面积,水深2.5时,圆锥形部分满水,圆柱形部分的高是2.5-1.5,据此求出两部分容积,加起来即可。
解:设圆柱和圆锥的底面积是x平方分米。
1.5x+1.5x×=36
2x=36
2x÷2=36÷2
x=18
18×(2.5-1.5)+18×1.5÷3
=18×1+27÷3
=18+9
=27(升)
故答案为:C
二、填空题
7. 【答案】18.84;25.12
【解析】侧面积:6.28×3=18.84(厘米);
底面半径:6.28÷3.14÷2=1(厘米);
表面积:18.84+3.14×1×1×2=18.84+6.28=25.12(平方厘米)。
故答案为:18.84;25.12.
8. 【答案】25.12
【解析】解:这个圆柱的高是8×3.14=25.12厘米。
故答案为:25.12。
9. 【答案】540
【解析】解:30×18=540(平方厘米)
10. 【答案】36;12
【解析】根据体积计算公式可知,等底等高的圆柱的体积是圆锥体积的3倍 ,
48÷(3+1)
=48÷4
=12
12×3=36
11. 【答案】502.4
【解析】解:底面半径:8÷2=4(厘米);
圆柱的高:80÷2÷4=10(厘米);
圆柱体积(长方体体积):3.14×42×10=502.4(立方厘米);
答:长方体的体积是502.4立方厘米.
故答案为:502.4.
将一个圆柱切开后拼成一个近似的长方体,高没变,体积没变;但拼成的长方体表面积比圆柱多了两个长方形的面积,这两个长方形的长都和圆柱的高相等,宽都和圆柱的底面半径相等;已知表面积增加了80平方厘米,就可求出圆柱的高是多少厘米,进而再求出圆柱的体积,即长方体的体积.
圆柱体切拼成近似的长方体要明确:高没变,体积没变;但长方体表面积比圆柱多了两个长方形的面积.
三、判断题
12. 【答案】错误
【解析】3×3=9倍,原题说法错误。
故答案为:错误。
13. 【答案】错误
【解析】解:圆柱的侧面积=底面周长×高,原题说法错误.
故答案为:错误
14. 【答案】正确
【解析】解:根据圆锥的特征可知:从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形.原题说法正确.
故答案为:正确
15. 【答案】错误
【解析】如果圆锥体积是圆柱体积的 , 只能得到二者底面积与高的积相等,无法得到一定等底等高。
16. 【答案】√
【解析】把一段圆柱体木料削成一个最大的圆锥,即削成的圆锥是与原圆柱体等底等高的圆锥,又知圆锥体积,即圆锥体积是与它等底等高圆柱体积的,销去的部分是圆柱体积的,故销去部分是圆锥的倍。
把圆柱体削成的最大圆锥体是与原圆柱体等底等高的圆锥体。
圆柱体积:
削成的圆锥体积:
销去的部分:
销去部分是圆锥体积的(倍)
所以原题说法正确。
四、解答题
17. 【答案】侧面积:47.1平方分米;体积:35.325立方分米
【解析】侧面积: 3×3.14×5=47.1(平方分米);底面半径:3÷2=1.5(分米);底面积 3.14×1.5×1.5=7.065(平方分米);体积 7.065×5=35.325(立方分米)
答:它的侧面积是47.1平方分米,体积是35.325立方分米。
【解析】(1)解: ×3.14×2 ×9
=×9×3.14×4
=3×3.14×4
=9.42×4
=37.68(cm )
(2)解:表面积:3.14×4×6+3.14×(4÷2) ×2
=3.14×24+3.14×4×2
=3.14×24+3.14×8
=3.14×(24+8)
=3.14×32
=100.48(cm )
体积:3.14×(4÷2) ×6
=3.14×4×6
=3.14×24
=75.36(cm )
19. 【答案】19.8立方厘米
【解析】
26.4÷(6+2)=3.3(平方厘米)
3.3×6=19.8(立方厘米)
答:瓶内药水的体积是19.8立方厘米。
20. 【答案】解:2厘米=0.02米,
×28.26×2.5÷(10×0.02)
=9.42×2.5÷0.2
=23.55÷0.2
=117.75(米)
答:能铺117.75米.
【解析】
要求能铺多少米,首先根据圆锥的体积公式:V=sh,求出沙堆的体积,把这堆沙铺在长方形的路面上就相当于一个长方体,只是形状改变了,但沙的体积没有变,因此,用沙的体积除以长方体的长与高的乘积就是所铺的长度.由此列式解答.
本题主要考查了学生对圆锥和长方体体积公式的掌握,注意题目中的单位.
刷题、找试卷就用考霸刷题宝APP(第页/共7页)
2
一、单项选择题
1. 圆柱的底面半径和高都扩大3倍,它的体积将扩大( )倍。
A. 3 B. 6 C. 9 D. 27
2. 把一个圆柱削成一个最大的圆锥,削去部分的体积是原体积的( )。
A. B. C.
3. 等底的圆柱和圆锥,圆锥的高是圆柱的3倍,那么它们的体积( )。
A. 圆柱小于圆锥 B. 相等 C. 圆柱大于圆锥
4. 下面的平面图形分别绕虚线旋转一周会形成圆柱的是( ).
A. B. C. D.
5. 小杰做了一个圆柱形容器和几个圆锥形容器,大小如下图所示(单位:cm),将圆柱内的水倒入( )圆锥内,正好倒满。
A. B. C.
6. 如图,用36L的水刚好把这个容器装满。如果水深2.5dm,则容器里有( )L的水。(容器的厚度忽略不计)
A. 18 B. 24 C. 27 D. 30
二、填空题
7. 一个圆柱的侧面展开得到一个长方形,长方形的长是6.28厘米,宽是3厘米,这个圆柱体的侧面积是 平方厘米,表面积是 平方厘米.
8. 一个圆柱的底面直径是8厘米,它的侧面展开正好是一个正方形,这个圆柱的高是 厘米。
9. 将一张长30厘米,宽18厘米的长方形白纸卷成一个圆柱,这个圆柱的侧面积是 平方厘米。
10. 等底等高的圆柱与圆锥,它们体积之和为48dm ,这个圆柱体积是 dm ,圆锥体积是 dm 。
11. 如图所示,把底面直径8厘米的圆柱切成若干等分,拼成一个近似的长方体.这个长方体的表面积比原来增加80平方厘米,那么长方体的体积是______立方厘米.
三、判断题
12. 一个圆锥的高不变,底面半径扩大到原来的3倍,这个圆锥的体积也扩大到原来的3倍。( )
13. 圆柱的侧面积等于底面积乘高。( )
14. 从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形。( )
15. 一个圆锥的体积是圆柱体积的 ,那么圆锥与圆柱一定等底等高。( )
16. 把一段圆柱体木料削成一个最大的圆锥,削去的部分是圆锥体的2倍。(______)
四、解答题
17. 一个圆柱体底面直径3分米,高5分米,它的侧面积和体积分别是多少
18. 求圆锥的体积,圆柱的表面积和体积。
(1)
(2)
19. 一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示。它的容积为26.4 cm 。瓶子正放时,瓶内药水液面高6 cm,瓶子倒放时,空余部分高2 cm,则瓶内药水的体积是多少立方厘米?
20. 一个圆锥形沙堆,底面积是28.26平方米,高是2.5米.用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
参考答案
一、单项选择题
1. 【答案】D
【解析】设原来圆柱的底面半径和高均为1,则有
π×32×3÷(π×12×1)
=27π÷π
=27
所以圆柱的底面半径和高都扩大3倍,它的体积将扩大27倍。
故答案为:D。
2. 【答案】C
【解析】设圆柱的体积是1,则
(1-)÷1
=÷1
=
所以削去部分的体积是原体积的。
故答案为:C。
3. 【答案】B
【解析】解:假设底面积都是S,圆柱的高是h,则圆锥的高是3h;圆柱的体积:Sh;圆锥的体积:S×3h×=Sh;体积相等.
故答案为:B
4. 【答案】C
【解析】解:C项中的图形绕虚线旋转一周会形成圆柱。
故答案为:C。
5. 【答案】A
【解析】解:3.14×(10÷2)2×6=3.14×150(cm3);
A:3.14×(10÷2)2×18×=3.14×150(cm3),正好倒满;
B:3.14×(12÷2)2×18×=3.14×216,不能正好倒满;
C:3.14×(10÷2)2×15×=3.14×125,不能正好倒满。
6. 【答案】C
【解析】这个容器有圆柱和圆锥两部分组成,且圆柱和圆锥的底面积相等,设圆柱和圆锥的底面积是x平方分米,根据圆柱容积+圆锥容积=36,列出方程,求出底面积,水深2.5时,圆锥形部分满水,圆柱形部分的高是2.5-1.5,据此求出两部分容积,加起来即可。
解:设圆柱和圆锥的底面积是x平方分米。
1.5x+1.5x×=36
2x=36
2x÷2=36÷2
x=18
18×(2.5-1.5)+18×1.5÷3
=18×1+27÷3
=18+9
=27(升)
故答案为:C
二、填空题
7. 【答案】18.84;25.12
【解析】侧面积:6.28×3=18.84(厘米);
底面半径:6.28÷3.14÷2=1(厘米);
表面积:18.84+3.14×1×1×2=18.84+6.28=25.12(平方厘米)。
故答案为:18.84;25.12.
8. 【答案】25.12
【解析】解:这个圆柱的高是8×3.14=25.12厘米。
故答案为:25.12。
9. 【答案】540
【解析】解:30×18=540(平方厘米)
10. 【答案】36;12
【解析】根据体积计算公式可知,等底等高的圆柱的体积是圆锥体积的3倍 ,
48÷(3+1)
=48÷4
=12
12×3=36
11. 【答案】502.4
【解析】解:底面半径:8÷2=4(厘米);
圆柱的高:80÷2÷4=10(厘米);
圆柱体积(长方体体积):3.14×42×10=502.4(立方厘米);
答:长方体的体积是502.4立方厘米.
故答案为:502.4.
将一个圆柱切开后拼成一个近似的长方体,高没变,体积没变;但拼成的长方体表面积比圆柱多了两个长方形的面积,这两个长方形的长都和圆柱的高相等,宽都和圆柱的底面半径相等;已知表面积增加了80平方厘米,就可求出圆柱的高是多少厘米,进而再求出圆柱的体积,即长方体的体积.
圆柱体切拼成近似的长方体要明确:高没变,体积没变;但长方体表面积比圆柱多了两个长方形的面积.
三、判断题
12. 【答案】错误
【解析】3×3=9倍,原题说法错误。
故答案为:错误。
13. 【答案】错误
【解析】解:圆柱的侧面积=底面周长×高,原题说法错误.
故答案为:错误
14. 【答案】正确
【解析】解:根据圆锥的特征可知:从圆锥的顶点向底面垂直切割,所得到的截面是一个等腰的三角形.原题说法正确.
故答案为:正确
15. 【答案】错误
【解析】如果圆锥体积是圆柱体积的 , 只能得到二者底面积与高的积相等,无法得到一定等底等高。
16. 【答案】√
【解析】把一段圆柱体木料削成一个最大的圆锥,即削成的圆锥是与原圆柱体等底等高的圆锥,又知圆锥体积,即圆锥体积是与它等底等高圆柱体积的,销去的部分是圆柱体积的,故销去部分是圆锥的倍。
把圆柱体削成的最大圆锥体是与原圆柱体等底等高的圆锥体。
圆柱体积:
削成的圆锥体积:
销去的部分:
销去部分是圆锥体积的(倍)
所以原题说法正确。
四、解答题
17. 【答案】侧面积:47.1平方分米;体积:35.325立方分米
【解析】侧面积: 3×3.14×5=47.1(平方分米);底面半径:3÷2=1.5(分米);底面积 3.14×1.5×1.5=7.065(平方分米);体积 7.065×5=35.325(立方分米)
答:它的侧面积是47.1平方分米,体积是35.325立方分米。
【解析】(1)解: ×3.14×2 ×9
=×9×3.14×4
=3×3.14×4
=9.42×4
=37.68(cm )
(2)解:表面积:3.14×4×6+3.14×(4÷2) ×2
=3.14×24+3.14×4×2
=3.14×24+3.14×8
=3.14×(24+8)
=3.14×32
=100.48(cm )
体积:3.14×(4÷2) ×6
=3.14×4×6
=3.14×24
=75.36(cm )
19. 【答案】19.8立方厘米
【解析】
26.4÷(6+2)=3.3(平方厘米)
3.3×6=19.8(立方厘米)
答:瓶内药水的体积是19.8立方厘米。
20. 【答案】解:2厘米=0.02米,
×28.26×2.5÷(10×0.02)
=9.42×2.5÷0.2
=23.55÷0.2
=117.75(米)
答:能铺117.75米.
【解析】
要求能铺多少米,首先根据圆锥的体积公式:V=sh,求出沙堆的体积,把这堆沙铺在长方形的路面上就相当于一个长方体,只是形状改变了,但沙的体积没有变,因此,用沙的体积除以长方体的长与高的乘积就是所铺的长度.由此列式解答.
本题主要考查了学生对圆锥和长方体体积公式的掌握,注意题目中的单位.
刷题、找试卷就用考霸刷题宝APP(第页/共7页)
2
