面积经典例题与过关练习(含答案)数学三年级下册北师大版
文档属性
| 名称 | 面积经典例题与过关练习(含答案)数学三年级下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 309.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
面积经典例题与过关练习-数学三年级下册北师大版
经典例题一 .一张长方形纸,长40厘米,宽31厘米。 (1)它的周长是多少厘米? (2)它的面积是多少平方厘米? (3)用它剪出边长是2厘米的小正方形,最多可以剪出多少个? 【答案】(1)142厘米 (2)1240平方厘米 (3)300个 【分析】(1)长方形的周长=(长+宽)×2,代入数据计算。 (2)长方形的面积=长×宽,代入数据计算。 (3)40÷2=20(个),31÷2=15(个)……1(厘米),则长方形的长里面有20个2厘米,宽里面有15个2厘米,一共可以剪出(20×15)个小正方形。 【详解】(1)(40+31)×2 =71×2 =142(厘米) 答:它的周长是142厘米。 (2)40×31=1240(平方厘米) 答:它的面积是1240平方厘米。 (3)40÷2=20(个) 31÷2=15(个)……1(厘米) 20×15=300(个) 答:最多可以剪出300个。 【点睛】本题考查长方形的周长和面积公式的应用,关键是熟记公式。 经典例题二 .淘气用一根铁丝正好围成一个长8分米,宽4分米的长方形,笑笑用同样长的铁丝围成一个正方形,这个正方形的面积是多少平方分米? 【答案】36平方分米 【分析】依据长方形的周长公式,求出这根铁丝的长度;再用这根铁丝的长度除以4,求出正方形的边长;再用边长乘边长,即可求出正方形的面积。 【详解】(8+4)×2 =12×2 =24(分米) 24÷4=6(分米) 6×6=36(平方分米) 答:这个正方形的面积是36平方分米。 【点睛】本题主要考查了对长方形和正方形的周长、面积公式的掌握情况。 经典例题三 .中心公园有一块空地如图所示。它的中央建一个边长为10米的正方形喷水池,其余铺上草坪。草坪的面积是多少平方米? 【答案】1400平方米 【分析】长方形的面积=长×宽,把数据代入公式计算出这块空地面积;正方形的面积=边长×边长,把数据代入公式计算出喷水池面积;空地面积减去喷水池的面积就是草坪面积。 【详解】60×25=1500(平方米) 10×10=100(平方米) 1500-100=1400(平方米) 答:草坪的面积是1400平方米。 【点睛】熟练掌握长方形和正方形面积的计算方法是解题的关键。
过关练习
1.爷爷有一块长22米,宽8米的长方形地,计划在这块地里圈出一块最大的正方形地种红薯,剩下的地种玉米,种玉米的面积是多少平方米?
2.爸爸打算粉刷小云的房间,有一面墙壁长6米,宽3米,墙上有一扇3平方米的窗户,现在要粉刷这面墙壁,要粉刷的面积是多少?
3.一个操场长为74米,宽为48米,扩建后长增加了23米。扩建后的操场比原来增加了多少平方米?
4.有一个长方形桃园,长60m,宽45m,里面栽了很多桃树,每棵桃树占地9m2。
(1)这个果园一共栽了多少棵桃树?
(2)平均每棵桃树产桃15千克,这个果园一共产桃多少千克?
5.洒水车每分行驶160米,洒水的宽度是8米。洒水车行驶5分,能给多大的地面洒水?
6.张伯伯家有一块长方形菜地,这块菜地的长是37米,宽比长少12米。这块菜地的面积是多少平方米?
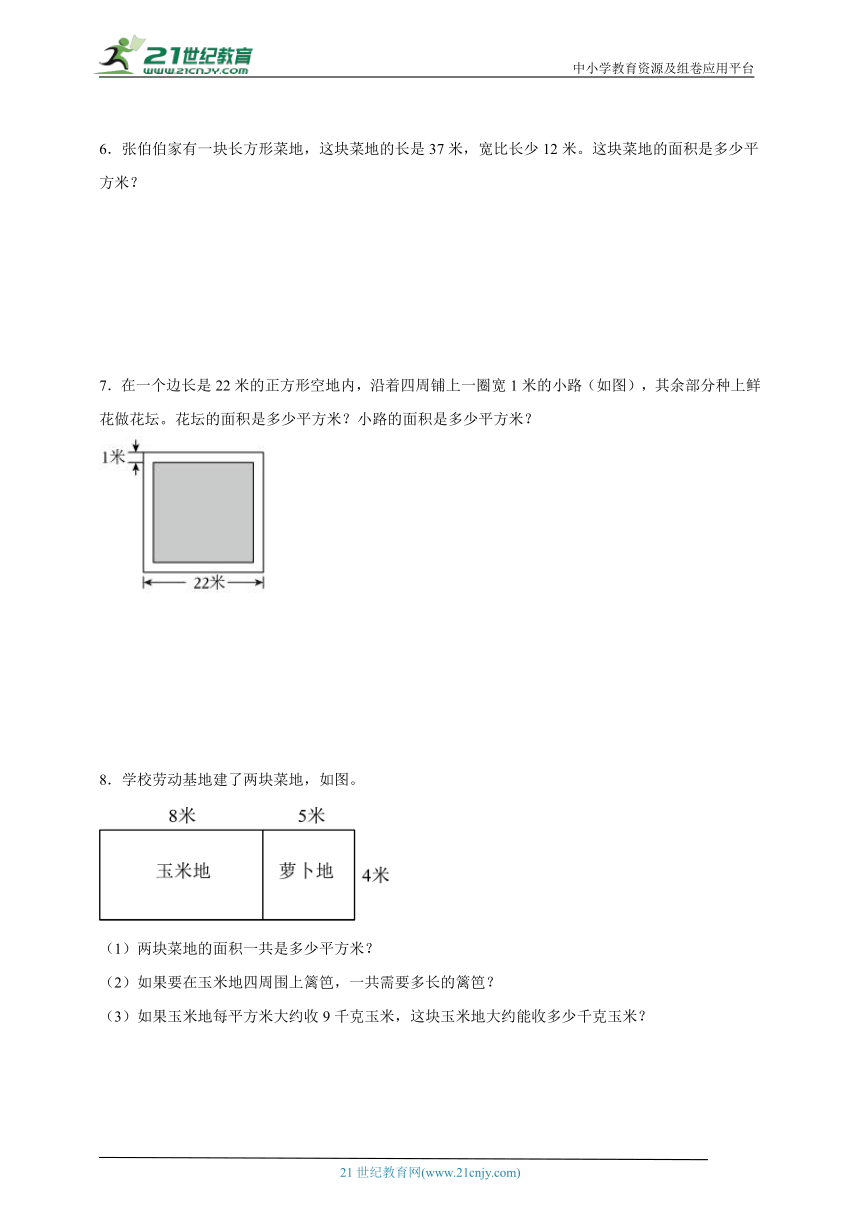
7.在一个边长是22米的正方形空地内,沿着四周铺上一圈宽1米的小路(如图),其余部分种上鲜花做花坛。花坛的面积是多少平方米?小路的面积是多少平方米?
8.学校劳动基地建了两块菜地,如图。
(1)两块菜地的面积一共是多少平方米?
(2)如果要在玉米地四周围上篱笆,一共需要多长的篱笆?
(3)如果玉米地每平方米大约收9千克玉米,这块玉米地大约能收多少千克玉米?
9.公路旁有一个长方形鱼池的长是30米。今年因扩建公路,长减少了5米,鱼池面积就减少了 100 平方米,原来鱼池的面积是多少平方米?(先面出示意图,再列式解答)
10.如图,将一张边长为16厘米的大正方形纸,剪成4个完全一样的小正方形纸片,每个小正方形纸片的周长和面积分别是多少?
11.晶晶家的一块菜地如图所示:
(1)如果在菜地的中间挖一个边长是5米的正方形蓄水池,这个蓄水池的占地面积是多少?
(2)请你求出种菜部分的面积。
(3)如果蓄水池挖在下图所示的位置,你知道种菜部分的面积吗?种菜部分的周长呢?
12.长方形和正方形有一部分重合(如图),两个图形中阴影部分的面积相差多少平方厘米?
参考答案:
1.112平方米
【分析】长方形中圈出最大的正方形,正方形的边长等于长方形的宽,所以种红薯地块的边长等于8米,8乘8等于种红薯地块的面积,22乘8等于长方形地块的面积,长方形地块的面积减种红薯地块的面积,即等于种玉米的面积,据此即可解答。
【详解】22×8-8×8
=176-64
=112(平方米)
答:种玉米的面积是112平方米。
2.15平方米
【分析】根据长方形的面积=长×宽,求出这面墙壁的面积是多少平方米,再用这面墙壁的面积减去窗户的面积就是要粉刷的面积。
【详解】6×3-3
=18-3
=15(平方米)
答:要粉刷的面积是15平方米。
3.1104平方米
【分析】宽不变,长增加23米,则面积增加部分是长48米宽23米的长方形的面积,根据长方形的面积=长×宽解答。
【详解】48×23=1104(平方米)
答:扩建后的操场比原来增加了1104平方米。
4.(1)300棵
(2)4500千克
【分析】(1)根据长方形面积=长×宽,用60×45先求出桃园的面积,再除以每棵桃树的占地面积即可求出这个果园一共栽了多少棵桃树。
(2)用桃树的总棵树乘平均每棵桃树产桃的重量,即可求出这个果园一共产桃多少千克。
【详解】60×45=2700(m2)
2700÷9=300(棵)
答:这个果园一共栽了300棵桃树。
(2)300×15=4500(千克)
答:这个果园一共产桃4500千克。
5.6400平方米
【分析】根据题意可知,洒水车每分行驶的路程×洒水的宽度=洒水车每分钟洒水的面积,洒水车每分钟洒水的面积×5=洒水车5分钟洒水的面积,依此计算。
【详解】160×8=1280(平方米)
1280×5=6400(平方米)
答:洒水车行驶5分,能给6400平方米的地面洒水。
6.925平方米
【分析】宽比长少12米,用长减12就是宽,再根据长方形的面积公式计算即可,长方形的面积=长×宽。
【详解】37-12=25(米)
37×25=925(平方米)
答:这块菜地的面积是925平方米。
7.400平方米;84平方米
【分析】(1)花坛四周都要铺上小路,则花坛的边长是(22-1-1)米,再根据正方形的面积公式:正方形面积=边长×边长,列式计算即可解决问题。
(2)根据正方形的面积公式求出边长是22米的大正方形的面积,再减去花坛的面积就是小路的面积。
【详解】22-1-1=20(米)
20×20=400(平方米)
22×22-400
=484-400
=84(平方米)
答:花坛的面积是400平方米,小路的面积是84平方米。
8.(1)52平方米
(2)24米
(3)288千克
【分析】(1)这两块地的总面积是一个长(8+5)米,宽4米的长方形的面积,根据长方形的面积=长×宽解答。
(2)长方形的周长=(长+宽)×2,据此求出篱笆长度。
(3)根据长方形的面积=长×宽,求出玉米地的面积,再乘每平方米收玉米重量,求出这块玉米地收玉米总重量。
【详解】(1)(8+5)×4
=13×4
=52(平方米)
答:两块菜地的面积一共是52平方米。
(2)(8+4)×2
=12×2
=24(米)
答:一共需要24米长的篱笆。
(3)8×4×9
=32×9
=288(千克)
答:这块玉米地大约能收288千克玉米。
9.600平方米(图见分析)
【分析】如下图,鱼池减少的面积除以长减少的长度等于鱼池的宽,鱼池原来的长乘宽即等于原来鱼池的面积,据此即可解答。
【详解】100÷5×30
=20×30
=600(平方米)
答:原来鱼池的面积是600平方米。
【点睛】先计算出鱼池的宽是解答本题的关键。
10.32厘米;64平方厘米
【分析】根据题意可知,小正方形纸片的边长为(16÷2)厘米。根据正方形的周长=边长×4和正方形的面积=边长×边长,解答即可。
【详解】16÷2=8(厘米)
8×4=32(厘米)
8×8=64(平方厘米)
答:每个小正方形纸片的周长是32厘米,面积是64平方厘米。
【点睛】熟练掌握正方形的周长和面积公式。明确小正方形纸片的边长为8厘米是解决本题的关键。
11.(1)25平方米
(2)1475平方米
(3)种菜部分的面积不变,为1475平方米。周长:170米。
【分析】(1)依据正方形的面积公式S=a×a即可求解;
(2)长方形的面积减去正方形的面积就是种菜部分的面积,利用长方形的面积S=ab和正方形的面积公式S=a×a即可求解。
(3)挖的正方形蓄水池的面积不变,故种菜部分面积不变,周长等于长方形的周长加上正方形的两条边。
【详解】(1)5×5=25(平方米)
答:蓄水池的占地面积为25平方米。
(2)50×30-25=1475(平方米)
答:种菜部分的面积为1475平方米。
(3)种菜部分的面积不变,为1475平方米。
周长:(30+50)×2+5×2=170(米)
答:种菜部分的面积不变,为1475平方米,种菜部分的周长为170米。
【点睛】此题考查了长方形、正方形周长和面积公式的灵活运用。
12.2平方厘米
【分析】因重合的部分是公共部分,面积相等,所以两块没有重合的阴影部分的面积差就是大长方形的面积与小正方形面积的差。然后根据长方形面积=长×宽,正方形面积=边长×边长,代入数据解答即可。
【详解】2×3﹣2×2
=6﹣4
=2(平方厘米)
答:两个图形中阴影部分的面积相差2平方厘米。
【点睛】本题的关键是让学生理解两块没有重合的阴影部分的面积差就是大长方形的面积与小正方形的面积的差。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
面积经典例题与过关练习-数学三年级下册北师大版
经典例题一 .一张长方形纸,长40厘米,宽31厘米。 (1)它的周长是多少厘米? (2)它的面积是多少平方厘米? (3)用它剪出边长是2厘米的小正方形,最多可以剪出多少个? 【答案】(1)142厘米 (2)1240平方厘米 (3)300个 【分析】(1)长方形的周长=(长+宽)×2,代入数据计算。 (2)长方形的面积=长×宽,代入数据计算。 (3)40÷2=20(个),31÷2=15(个)……1(厘米),则长方形的长里面有20个2厘米,宽里面有15个2厘米,一共可以剪出(20×15)个小正方形。 【详解】(1)(40+31)×2 =71×2 =142(厘米) 答:它的周长是142厘米。 (2)40×31=1240(平方厘米) 答:它的面积是1240平方厘米。 (3)40÷2=20(个) 31÷2=15(个)……1(厘米) 20×15=300(个) 答:最多可以剪出300个。 【点睛】本题考查长方形的周长和面积公式的应用,关键是熟记公式。 经典例题二 .淘气用一根铁丝正好围成一个长8分米,宽4分米的长方形,笑笑用同样长的铁丝围成一个正方形,这个正方形的面积是多少平方分米? 【答案】36平方分米 【分析】依据长方形的周长公式,求出这根铁丝的长度;再用这根铁丝的长度除以4,求出正方形的边长;再用边长乘边长,即可求出正方形的面积。 【详解】(8+4)×2 =12×2 =24(分米) 24÷4=6(分米) 6×6=36(平方分米) 答:这个正方形的面积是36平方分米。 【点睛】本题主要考查了对长方形和正方形的周长、面积公式的掌握情况。 经典例题三 .中心公园有一块空地如图所示。它的中央建一个边长为10米的正方形喷水池,其余铺上草坪。草坪的面积是多少平方米? 【答案】1400平方米 【分析】长方形的面积=长×宽,把数据代入公式计算出这块空地面积;正方形的面积=边长×边长,把数据代入公式计算出喷水池面积;空地面积减去喷水池的面积就是草坪面积。 【详解】60×25=1500(平方米) 10×10=100(平方米) 1500-100=1400(平方米) 答:草坪的面积是1400平方米。 【点睛】熟练掌握长方形和正方形面积的计算方法是解题的关键。
过关练习
1.爷爷有一块长22米,宽8米的长方形地,计划在这块地里圈出一块最大的正方形地种红薯,剩下的地种玉米,种玉米的面积是多少平方米?
2.爸爸打算粉刷小云的房间,有一面墙壁长6米,宽3米,墙上有一扇3平方米的窗户,现在要粉刷这面墙壁,要粉刷的面积是多少?
3.一个操场长为74米,宽为48米,扩建后长增加了23米。扩建后的操场比原来增加了多少平方米?
4.有一个长方形桃园,长60m,宽45m,里面栽了很多桃树,每棵桃树占地9m2。
(1)这个果园一共栽了多少棵桃树?
(2)平均每棵桃树产桃15千克,这个果园一共产桃多少千克?
5.洒水车每分行驶160米,洒水的宽度是8米。洒水车行驶5分,能给多大的地面洒水?
6.张伯伯家有一块长方形菜地,这块菜地的长是37米,宽比长少12米。这块菜地的面积是多少平方米?
7.在一个边长是22米的正方形空地内,沿着四周铺上一圈宽1米的小路(如图),其余部分种上鲜花做花坛。花坛的面积是多少平方米?小路的面积是多少平方米?
8.学校劳动基地建了两块菜地,如图。
(1)两块菜地的面积一共是多少平方米?
(2)如果要在玉米地四周围上篱笆,一共需要多长的篱笆?
(3)如果玉米地每平方米大约收9千克玉米,这块玉米地大约能收多少千克玉米?
9.公路旁有一个长方形鱼池的长是30米。今年因扩建公路,长减少了5米,鱼池面积就减少了 100 平方米,原来鱼池的面积是多少平方米?(先面出示意图,再列式解答)
10.如图,将一张边长为16厘米的大正方形纸,剪成4个完全一样的小正方形纸片,每个小正方形纸片的周长和面积分别是多少?
11.晶晶家的一块菜地如图所示:
(1)如果在菜地的中间挖一个边长是5米的正方形蓄水池,这个蓄水池的占地面积是多少?
(2)请你求出种菜部分的面积。
(3)如果蓄水池挖在下图所示的位置,你知道种菜部分的面积吗?种菜部分的周长呢?
12.长方形和正方形有一部分重合(如图),两个图形中阴影部分的面积相差多少平方厘米?
参考答案:
1.112平方米
【分析】长方形中圈出最大的正方形,正方形的边长等于长方形的宽,所以种红薯地块的边长等于8米,8乘8等于种红薯地块的面积,22乘8等于长方形地块的面积,长方形地块的面积减种红薯地块的面积,即等于种玉米的面积,据此即可解答。
【详解】22×8-8×8
=176-64
=112(平方米)
答:种玉米的面积是112平方米。
2.15平方米
【分析】根据长方形的面积=长×宽,求出这面墙壁的面积是多少平方米,再用这面墙壁的面积减去窗户的面积就是要粉刷的面积。
【详解】6×3-3
=18-3
=15(平方米)
答:要粉刷的面积是15平方米。
3.1104平方米
【分析】宽不变,长增加23米,则面积增加部分是长48米宽23米的长方形的面积,根据长方形的面积=长×宽解答。
【详解】48×23=1104(平方米)
答:扩建后的操场比原来增加了1104平方米。
4.(1)300棵
(2)4500千克
【分析】(1)根据长方形面积=长×宽,用60×45先求出桃园的面积,再除以每棵桃树的占地面积即可求出这个果园一共栽了多少棵桃树。
(2)用桃树的总棵树乘平均每棵桃树产桃的重量,即可求出这个果园一共产桃多少千克。
【详解】60×45=2700(m2)
2700÷9=300(棵)
答:这个果园一共栽了300棵桃树。
(2)300×15=4500(千克)
答:这个果园一共产桃4500千克。
5.6400平方米
【分析】根据题意可知,洒水车每分行驶的路程×洒水的宽度=洒水车每分钟洒水的面积,洒水车每分钟洒水的面积×5=洒水车5分钟洒水的面积,依此计算。
【详解】160×8=1280(平方米)
1280×5=6400(平方米)
答:洒水车行驶5分,能给6400平方米的地面洒水。
6.925平方米
【分析】宽比长少12米,用长减12就是宽,再根据长方形的面积公式计算即可,长方形的面积=长×宽。
【详解】37-12=25(米)
37×25=925(平方米)
答:这块菜地的面积是925平方米。
7.400平方米;84平方米
【分析】(1)花坛四周都要铺上小路,则花坛的边长是(22-1-1)米,再根据正方形的面积公式:正方形面积=边长×边长,列式计算即可解决问题。
(2)根据正方形的面积公式求出边长是22米的大正方形的面积,再减去花坛的面积就是小路的面积。
【详解】22-1-1=20(米)
20×20=400(平方米)
22×22-400
=484-400
=84(平方米)
答:花坛的面积是400平方米,小路的面积是84平方米。
8.(1)52平方米
(2)24米
(3)288千克
【分析】(1)这两块地的总面积是一个长(8+5)米,宽4米的长方形的面积,根据长方形的面积=长×宽解答。
(2)长方形的周长=(长+宽)×2,据此求出篱笆长度。
(3)根据长方形的面积=长×宽,求出玉米地的面积,再乘每平方米收玉米重量,求出这块玉米地收玉米总重量。
【详解】(1)(8+5)×4
=13×4
=52(平方米)
答:两块菜地的面积一共是52平方米。
(2)(8+4)×2
=12×2
=24(米)
答:一共需要24米长的篱笆。
(3)8×4×9
=32×9
=288(千克)
答:这块玉米地大约能收288千克玉米。
9.600平方米(图见分析)
【分析】如下图,鱼池减少的面积除以长减少的长度等于鱼池的宽,鱼池原来的长乘宽即等于原来鱼池的面积,据此即可解答。
【详解】100÷5×30
=20×30
=600(平方米)
答:原来鱼池的面积是600平方米。
【点睛】先计算出鱼池的宽是解答本题的关键。
10.32厘米;64平方厘米
【分析】根据题意可知,小正方形纸片的边长为(16÷2)厘米。根据正方形的周长=边长×4和正方形的面积=边长×边长,解答即可。
【详解】16÷2=8(厘米)
8×4=32(厘米)
8×8=64(平方厘米)
答:每个小正方形纸片的周长是32厘米,面积是64平方厘米。
【点睛】熟练掌握正方形的周长和面积公式。明确小正方形纸片的边长为8厘米是解决本题的关键。
11.(1)25平方米
(2)1475平方米
(3)种菜部分的面积不变,为1475平方米。周长:170米。
【分析】(1)依据正方形的面积公式S=a×a即可求解;
(2)长方形的面积减去正方形的面积就是种菜部分的面积,利用长方形的面积S=ab和正方形的面积公式S=a×a即可求解。
(3)挖的正方形蓄水池的面积不变,故种菜部分面积不变,周长等于长方形的周长加上正方形的两条边。
【详解】(1)5×5=25(平方米)
答:蓄水池的占地面积为25平方米。
(2)50×30-25=1475(平方米)
答:种菜部分的面积为1475平方米。
(3)种菜部分的面积不变,为1475平方米。
周长:(30+50)×2+5×2=170(米)
答:种菜部分的面积不变,为1475平方米,种菜部分的周长为170米。
【点睛】此题考查了长方形、正方形周长和面积公式的灵活运用。
12.2平方厘米
【分析】因重合的部分是公共部分,面积相等,所以两块没有重合的阴影部分的面积差就是大长方形的面积与小正方形面积的差。然后根据长方形面积=长×宽,正方形面积=边长×边长,代入数据解答即可。
【详解】2×3﹣2×2
=6﹣4
=2(平方厘米)
答:两个图形中阴影部分的面积相差2平方厘米。
【点睛】本题的关键是让学生理解两块没有重合的阴影部分的面积差就是大长方形的面积与小正方形的面积的差。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
