江苏省苏州市第五中学2015-2016学年高二上学期期中考试数学试题
文档属性
| 名称 | 江苏省苏州市第五中学2015-2016学年高二上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 189.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-20 23:41:40 | ||
图片预览



文档简介
苏州五中2015-2016学年第一学期期中考试
高二数学
2015.11
注意事项:
1.本试卷分填空题和解答题两部分,共160分,考试用时120分钟.
2.答题前,考生务必将自己的班级、姓名、学号写在答题纸的密封线内.答题时,填空题和解答题的答案写在答题纸对应的位置上,答案写在试卷上无效,本卷考试结束后,上交答题纸.
一、填空题(本大题共14小题,每小题5分,共70分)
点到直线的距离是 ▲ .
若三个球的半径之比是,则它们的体积之比是 ▲ .
过点且垂直于直线的直线方程为 ▲ .
若三条直线两两互相垂直,则下列结论正确的是 ▲ .
①这三条直线共点; ②其中必有两条直线是异面直线;
③三条直线不可能在同一平面内; ④其中必有两条在同一平面内.
方程表示圆,则的取值范围是 ▲ .
已知是不重合的直线,是不重合的平面,则下列命题中正确的序号为 ▲ .
(1)若,则;
(2)若,则;
(3)若,则;
(4)若,则.
已知正三棱锥P—ABC中,侧棱,D、E分别是侧棱PB、PC上的点,则的周长的最小值是 ▲ .
直线l经过点,且在两坐标轴上的截距相等,则直线l的方程是 ▲ .
若,则直线2cos+3y+1=0的倾斜角的取值范围 ▲ .
点,到平面的距离分别为和,则线段的中点到平面的距离为 ▲ .
已知球O的面上有四点A、B、C、D,DA平面ABC,ABBC,DA=AB=BC=,则球O的体积等于 ▲ .
已知,,是直线上的动点,则的最小值为 ▲ .
若圆与圆相交,则m的取值范围是
▲ .
若直线y=x+b与曲线x=恰有一个公共点,则b的取值范围是 ▲ .
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
(本题14分)
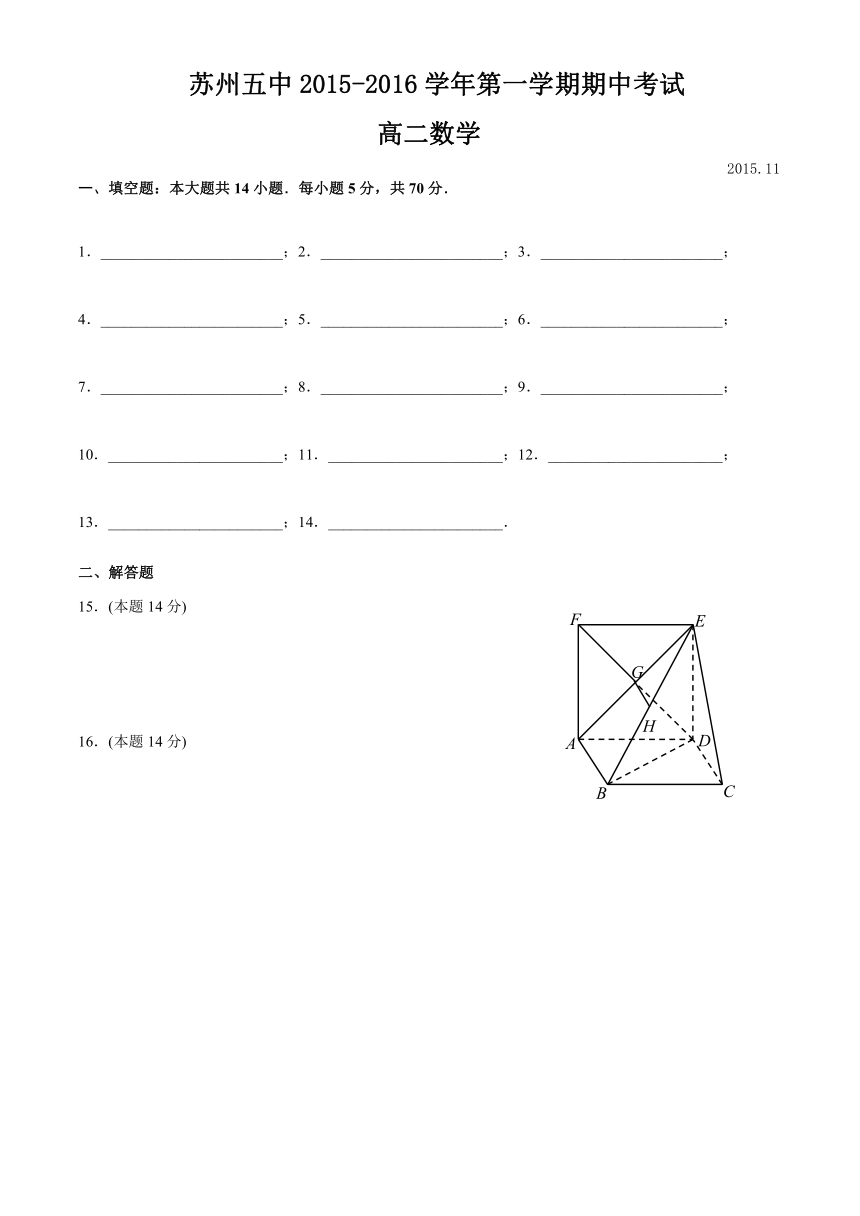
如图,在平行四边形ABCD中,BD⊥CD,正方形ADEF所在的平面和平面ABCD垂直,点H是BE的中点,点G是AE、DF的交点.
求证:GH∥平面CDE;
求证:BD⊥平面CDE.
(本题满分14分)
已知直线,.
求两直线的交点P;
求经过点P且平行于直线的直线方程;
求以点P为圆心,且与直线相切的圆的标准方程.
(本题满分14分)
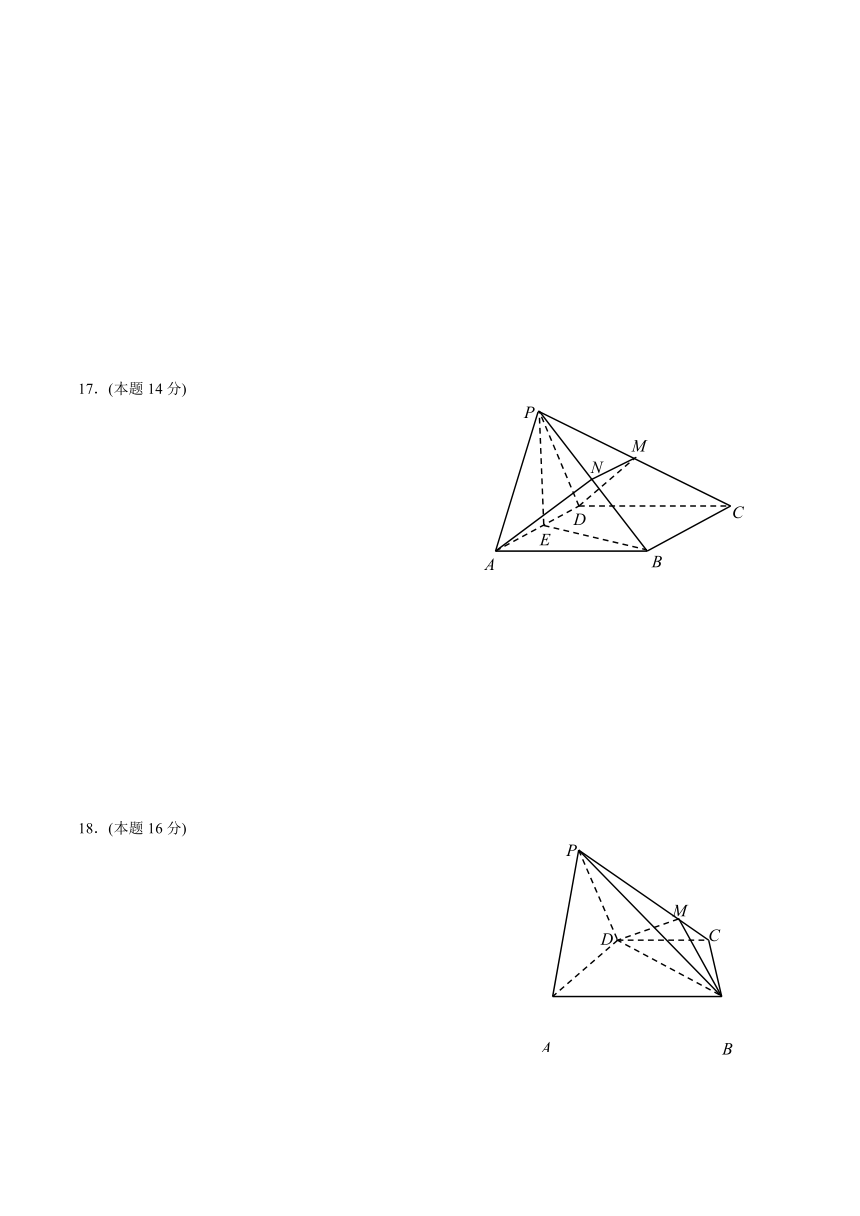
如图,在四棱锥中,侧面是正三角形,且与底面垂直,底面是边长为2的菱形,,是中点,截面交于,是中点,求证:
;
平面;
平面.
.(本题满分16分)
如图,在四棱锥中,平面平面,,是等边三角形,已知,,.
设是上的一点,证明:平面平面;
当点位于线段PC什么位置时,平面?
求四棱锥的体积.
(本题满分16分)
已知圆C:,直线.
无论m取任何实数,直线必经过一个定点P,求出定点P的坐标;
过点P作圆C的切线,求切线方程;
以CP为直径的圆与圆C交于A、B两点,求线段AB的长.
(本题满分16分)
方程的一个根在(0,1)内,另一个根在(1,2)内,求:
的值域;
的值域;
的值域.
苏州五中2015-2016学年第一学期期中考试
高二数学
2015.11
一、填空题:本大题共14小题.每小题5分,共70分.
1.________________________;2.________________________;3.________________________;
4.________________________;5.________________________;6.________________________;
7.________________________;8.________________________;9.________________________;
10._______________________;11._______________________;12._______________________;
13._______________________;14._______________________.
二、解答题
15.(本题14分)
16.(本题14分)
17.(本题14分)
18.(本题16分)
19.(本题16分)
20.(本题16分)
苏州五中2015-2016学年第一学期期中考试
高二数学 (参考答案)
2015.11
一、填空题(本大题共14小题,每小题5分,共70分)
1.; 2.; 3.; 4.③;
5.; 6.; 7.; 8.;
9.; 10.或; 11.; 12.;
13.; 14..
二、解答题
15.(本题满分14分)
证明 (1)因为G是AE与DF的交点,
所以G是AE的中点.…………2分
又H是BE的中点,
所以在△EAB中,GH∥AB. …………4分
因为AB∥CD,
所以GH∥CD. …………5分
又CD 平面CDE,GH 平面CDE,
所以GH∥平面CDE. …………7分
(2)平面ADEF⊥平面ABCD,交线为AD,
因为ED⊥AD,ED 平面ADEF,
所以ED⊥平面ABCD. …………10分
所以ED⊥BD. …………11分
又BD⊥CD,CD∩ED=D,
所以BD⊥平面CDE. …………14分
16.(本题满分14分)
解:(1)由,得,
所以…………4分
(2)设,…………5分
则…………6分
为所求…………8分
(3) …………10分
因为相切,所以半径…………12分
所以圆方程为…………14分
17.(本题满分14分)
证明:(1)∵,平面,
∴平面,…………2分
∵平面,
平面平面,
∴.…………4分
(2)连结
∵和都是正三角形,
∴,,又,…………6分
∴平面,…………7分
(3)又平面,…………9分
∴,…………10分
∵,是中点,
∴,…………12分
又,
∴⊥平面.…………14分
18.(本题满分16分)
证明:(1)在中,
∵,,,∴.
∴.…………2分
又 ∵平面平面,
平面平面,平面,
∴平面.
又平面,
∴平面平面.…………4分
(2)当点位于线段PC靠近C点的三等分点处时,平面.……5分
证明如下:连接AC,交于点N,连接MN.
∵,所以四边形是梯形.
∵,∴.
又 ∵,
∴,∴MN.…………7分
∵平面,∴平面.…………9分
(3)过作交于,
∵平面平面,
∴平面.
即为四棱锥的高.…………11分
又 ∵是边长为4的等边三角形,∴.…………12分
在中,斜边边上的高为,此即为梯形的高.
∴梯形的面积.…………14分
故.…………16分
19.(本题满分16分)
解:(1) 直线:
可变形…………2分
。
因此直线恒过定点P(-2,2)…………5分
(2)因为
所以点P在圆外…………6分
若切线斜率不存在,
则切线方程为,经检验,成立…………7分
②若切线斜率存在,则设切线方程为
因为,所以
解得
即切线方程为…………10分
综上,切线方程为或…………11分
(3)以CP为直径的圆的方程为…………13分
所以公共弦AB所在直线方程为…………14分
圆心C到直线AB的距离…………15分
所以…………16分
20.(本题满分16分)
解:由题意:,…………3分
画出可行域…………7分
可行域是由A(-3,1)、B(-2,0)、C(-1,0)所构成的三角形区域,
利用各式的几何意义分别可得值域为:
(1)可行域内的点与点(1,2)的连线的斜率,
…………10分
(2)可行域内的点到点(1,2)的距离的平方
(8,17)…………13分
(3)为求目标函数的最值
.…………16分
高二数学
2015.11
注意事项:
1.本试卷分填空题和解答题两部分,共160分,考试用时120分钟.
2.答题前,考生务必将自己的班级、姓名、学号写在答题纸的密封线内.答题时,填空题和解答题的答案写在答题纸对应的位置上,答案写在试卷上无效,本卷考试结束后,上交答题纸.
一、填空题(本大题共14小题,每小题5分,共70分)
点到直线的距离是 ▲ .
若三个球的半径之比是,则它们的体积之比是 ▲ .
过点且垂直于直线的直线方程为 ▲ .
若三条直线两两互相垂直,则下列结论正确的是 ▲ .
①这三条直线共点; ②其中必有两条直线是异面直线;
③三条直线不可能在同一平面内; ④其中必有两条在同一平面内.
方程表示圆,则的取值范围是 ▲ .
已知是不重合的直线,是不重合的平面,则下列命题中正确的序号为 ▲ .
(1)若,则;
(2)若,则;
(3)若,则;
(4)若,则.
已知正三棱锥P—ABC中,侧棱,D、E分别是侧棱PB、PC上的点,则的周长的最小值是 ▲ .
直线l经过点,且在两坐标轴上的截距相等,则直线l的方程是 ▲ .
若,则直线2cos+3y+1=0的倾斜角的取值范围 ▲ .
点,到平面的距离分别为和,则线段的中点到平面的距离为 ▲ .
已知球O的面上有四点A、B、C、D,DA平面ABC,ABBC,DA=AB=BC=,则球O的体积等于 ▲ .
已知,,是直线上的动点,则的最小值为 ▲ .
若圆与圆相交,则m的取值范围是
▲ .
若直线y=x+b与曲线x=恰有一个公共点,则b的取值范围是 ▲ .
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
(本题14分)
如图,在平行四边形ABCD中,BD⊥CD,正方形ADEF所在的平面和平面ABCD垂直,点H是BE的中点,点G是AE、DF的交点.
求证:GH∥平面CDE;
求证:BD⊥平面CDE.
(本题满分14分)
已知直线,.
求两直线的交点P;
求经过点P且平行于直线的直线方程;
求以点P为圆心,且与直线相切的圆的标准方程.
(本题满分14分)
如图,在四棱锥中,侧面是正三角形,且与底面垂直,底面是边长为2的菱形,,是中点,截面交于,是中点,求证:
;
平面;
平面.
.(本题满分16分)
如图,在四棱锥中,平面平面,,是等边三角形,已知,,.
设是上的一点,证明:平面平面;
当点位于线段PC什么位置时,平面?
求四棱锥的体积.
(本题满分16分)
已知圆C:,直线.
无论m取任何实数,直线必经过一个定点P,求出定点P的坐标;
过点P作圆C的切线,求切线方程;
以CP为直径的圆与圆C交于A、B两点,求线段AB的长.
(本题满分16分)
方程的一个根在(0,1)内,另一个根在(1,2)内,求:
的值域;
的值域;
的值域.
苏州五中2015-2016学年第一学期期中考试
高二数学
2015.11
一、填空题:本大题共14小题.每小题5分,共70分.
1.________________________;2.________________________;3.________________________;
4.________________________;5.________________________;6.________________________;
7.________________________;8.________________________;9.________________________;
10._______________________;11._______________________;12._______________________;
13._______________________;14._______________________.
二、解答题
15.(本题14分)
16.(本题14分)
17.(本题14分)
18.(本题16分)
19.(本题16分)
20.(本题16分)
苏州五中2015-2016学年第一学期期中考试
高二数学 (参考答案)
2015.11
一、填空题(本大题共14小题,每小题5分,共70分)
1.; 2.; 3.; 4.③;
5.; 6.; 7.; 8.;
9.; 10.或; 11.; 12.;
13.; 14..
二、解答题
15.(本题满分14分)
证明 (1)因为G是AE与DF的交点,
所以G是AE的中点.…………2分
又H是BE的中点,
所以在△EAB中,GH∥AB. …………4分
因为AB∥CD,
所以GH∥CD. …………5分
又CD 平面CDE,GH 平面CDE,
所以GH∥平面CDE. …………7分
(2)平面ADEF⊥平面ABCD,交线为AD,
因为ED⊥AD,ED 平面ADEF,
所以ED⊥平面ABCD. …………10分
所以ED⊥BD. …………11分
又BD⊥CD,CD∩ED=D,
所以BD⊥平面CDE. …………14分
16.(本题满分14分)
解:(1)由,得,
所以…………4分
(2)设,…………5分
则…………6分
为所求…………8分
(3) …………10分
因为相切,所以半径…………12分
所以圆方程为…………14分
17.(本题满分14分)
证明:(1)∵,平面,
∴平面,…………2分
∵平面,
平面平面,
∴.…………4分
(2)连结
∵和都是正三角形,
∴,,又,…………6分
∴平面,…………7分
(3)又平面,…………9分
∴,…………10分
∵,是中点,
∴,…………12分
又,
∴⊥平面.…………14分
18.(本题满分16分)
证明:(1)在中,
∵,,,∴.
∴.…………2分
又 ∵平面平面,
平面平面,平面,
∴平面.
又平面,
∴平面平面.…………4分
(2)当点位于线段PC靠近C点的三等分点处时,平面.……5分
证明如下:连接AC,交于点N,连接MN.
∵,所以四边形是梯形.
∵,∴.
又 ∵,
∴,∴MN.…………7分
∵平面,∴平面.…………9分
(3)过作交于,
∵平面平面,
∴平面.
即为四棱锥的高.…………11分
又 ∵是边长为4的等边三角形,∴.…………12分
在中,斜边边上的高为,此即为梯形的高.
∴梯形的面积.…………14分
故.…………16分
19.(本题满分16分)
解:(1) 直线:
可变形…………2分
。
因此直线恒过定点P(-2,2)…………5分
(2)因为
所以点P在圆外…………6分
若切线斜率不存在,
则切线方程为,经检验,成立…………7分
②若切线斜率存在,则设切线方程为
因为,所以
解得
即切线方程为…………10分
综上,切线方程为或…………11分
(3)以CP为直径的圆的方程为…………13分
所以公共弦AB所在直线方程为…………14分
圆心C到直线AB的距离…………15分
所以…………16分
20.(本题满分16分)
解:由题意:,…………3分
画出可行域…………7分
可行域是由A(-3,1)、B(-2,0)、C(-1,0)所构成的三角形区域,
利用各式的几何意义分别可得值域为:
(1)可行域内的点与点(1,2)的连线的斜率,
…………10分
(2)可行域内的点到点(1,2)的距离的平方
(8,17)…………13分
(3)为求目标函数的最值
.…………16分
同课章节目录
