八年级数学下册试题22.3 特殊平行四边形--动态几何-沪教版(含答案)
文档属性
| 名称 | 八年级数学下册试题22.3 特殊平行四边形--动态几何-沪教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 00:00:00 | ||
图片预览



文档简介
22.3 特殊平行四边形--动态几何
一、解答题
1.如图1,正方形的边长为1,为边上一点(不与点、重合),垂直于的一条直线分别交、、于点、、.
(1)①求证:;
②连接、、,直接写出四边形的面积S的取值范围.
(2)如图2,若垂足为的中点,连接,交于点,连接,求的度数.
(3)如图3,当垂足在正方形的对角线上时,作,垂足为,点在边上运动过程中,的长度是否变化?若不变,求出的长;若变化,说明变化规律.
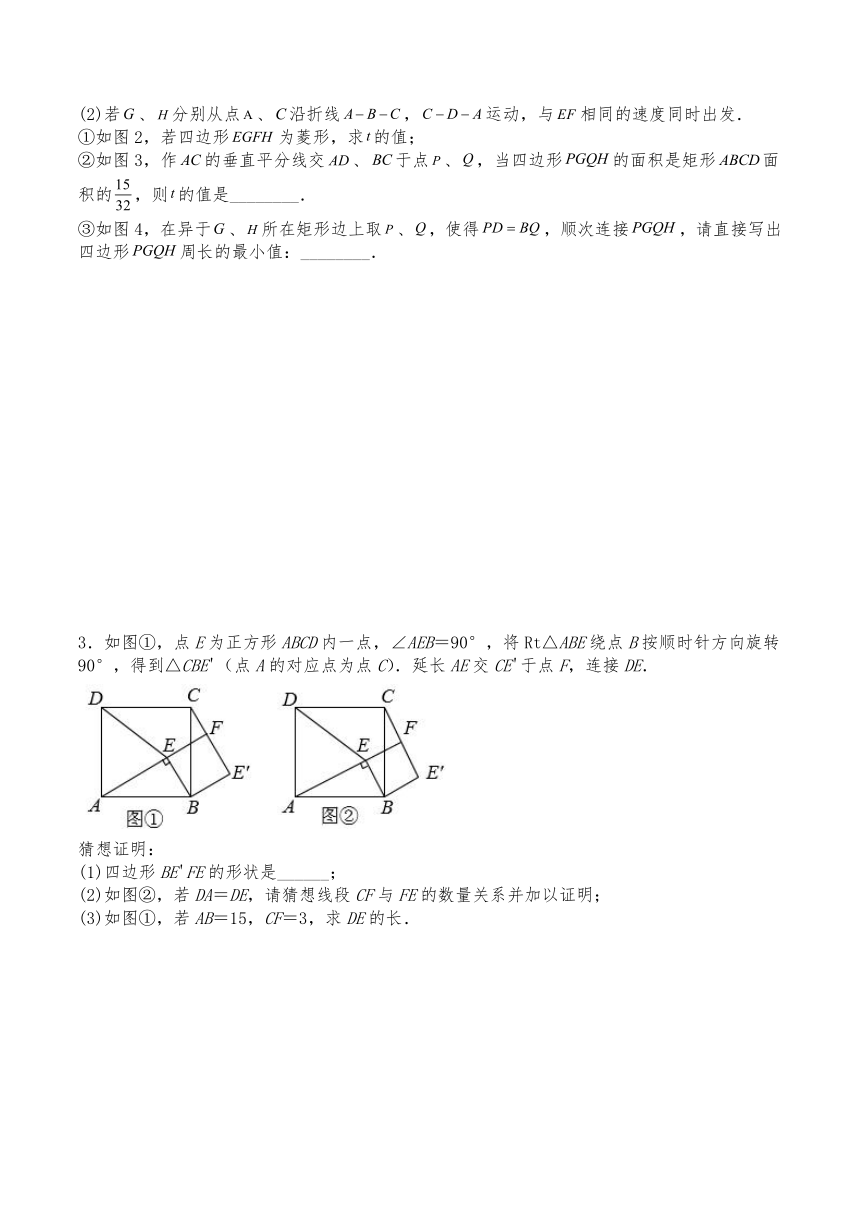
2.在矩形中,,,、是直线上的两个动点,分别从、两点同时出发相向而行,速度均为每秒2个单位长度,运动时间为秒,其中.
(1)如图1,、分别是、中点,当四边形是矩形时,求的值.
(2)若、分别从点、沿折线,运动,与相同的速度同时出发.
①如图2,若四边形为菱形,求的值;
②如图3,作的垂直平分线交、于点、,当四边形的面积是矩形面积的,则的值是________.
③如图4,在异于、所在矩形边上取、,使得,顺次连接,请直接写出四边形周长的最小值:________.
3.如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C).延长AE交CE'于点F,连接DE.
猜想证明:
(1)四边形BE'FE的形状是______;
(2)如图②,若DA=DE,请猜想线段CF与FE的数量关系并加以证明;
(3)如图①,若AB=15,CF=3,求DE的长.
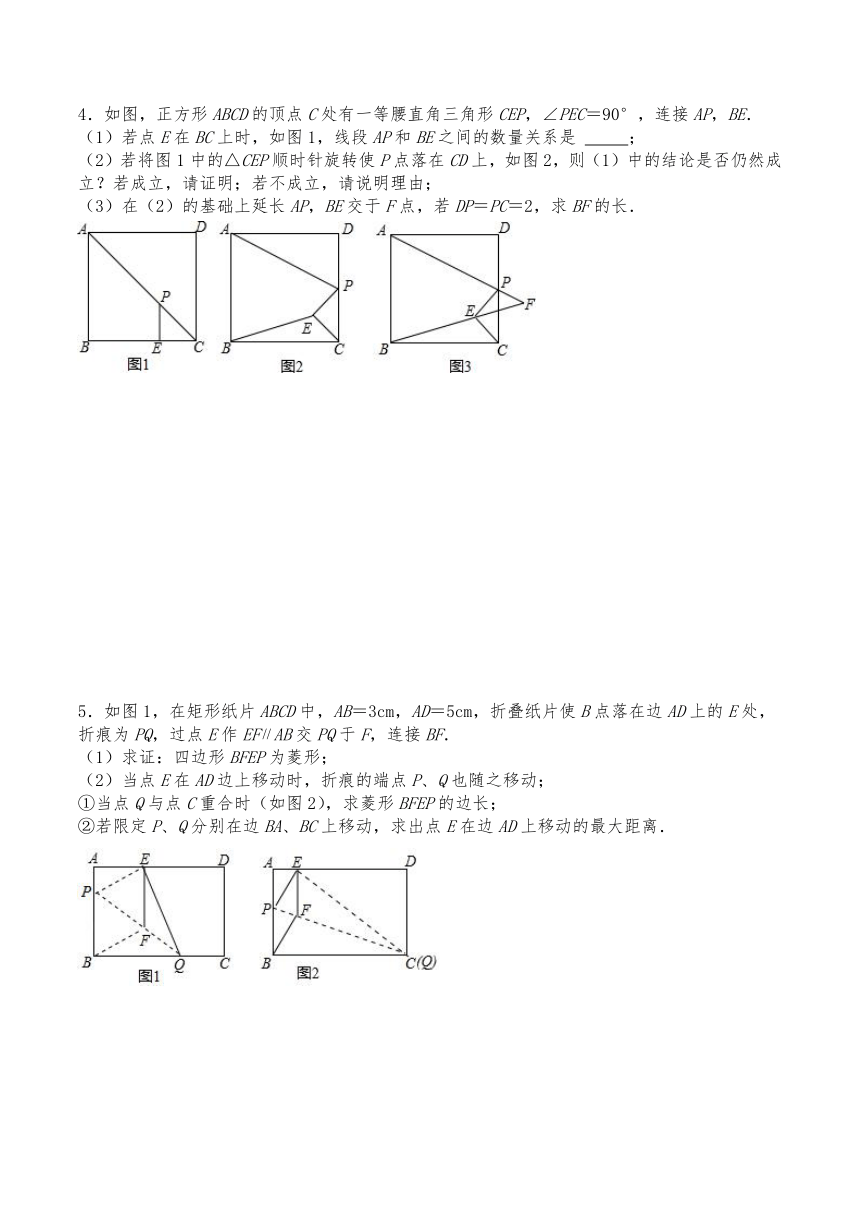
4.如图,正方形ABCD的顶点C处有一等腰直角三角形CEP,∠PEC=90°,连接AP,BE.
(1)若点E在BC上时,如图1,线段AP和BE之间的数量关系是 ;
(2)若将图1中的△CEP顺时针旋转使P点落在CD上,如图2,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在(2)的基础上延长AP,BE交于F点,若DP=PC=2,求BF的长.
5.如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EFAB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
6.如图所示,在正方形ABCD中,点E是边AB上一动点(不与A,B重合),延长BA至点F,使AF=BE,连接CE,DF.
(1) 判断四边形CEFD的形状,并说明理由;
(2) 如图①,连接AC,过点E作EH⊥AC,垂足为点H.
①证明:AH=EH;
②若BE:AE=1:,求∠BCE的度数;
③如图②,连接FH,在点E的运动过程中,的值是否发生变化?若不变,求出的值;若变化,请说明理由.
7.已知,四边形和四边形都是正方形,点为的中点.
(1)连接、.
①如图1,若点在边上,猜想和的关系,并给予证明:
②若将图1中的正方形绕点顺时针旋转,使点落在对角线的延长线上,请你在图2中补全图形,猜想和的关系,并给予证明.
(2)如图3,若,,将正方形绕点旋转,连接.请你直接写出的取值范围___________.
8.如图1所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形.现将小长方形绕点C顺时针旋转至,旋转角为.
(1)当点恰好落在边上时,点到边的距离为____________,旋转角____________;
(2)如图2,G为的中点,且,求证:;
(3)小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.
9.如图,四边形为菱形,,,点E为边上动点(不含端点)点B关于直线的对称点为点F,点H为中点.
(1)若,求的长;
(2)作,垂足为G,当时,求的度数;
(3)在(2)的条件下,设射线交于M,求的长.
10.如图1,矩形ABCD中,AB=,AD=4,在BC边上取点E,使BE=AB,将△ABE向左平移到△DCF的位置,得到四边形AEFD.
(1)求证:四边形AEFD是菱形;
(2)如图2,将△DCF绕点D旋转至△DGA,连接GE,求线段GE的长;
(3)如图3,设P、Q分别是EF、AE上的两点,且∠PDQ=67.5°,试探究线段PF、AQ、PQ之间的数量关系,并说明理由.
11.如图,在菱形ABCD中,∠ABC=120°,AB=4,E为对角线AC上的动点(点E不与A,C重合),连接BE,将射线EB绕点E逆时针旋转120°后交射线AD于点F.
(1)如图1,当AE=AF时,求∠AEB的度数;
(2)如图2,分别过点B,F作EF,BE的平行线,且两直线相交于点G.
①试探究四边形BGFE的形状,并求出四边形BGFE的周长的最小值;
②连接AG,设CE=x,AG=y,请直接写出y与x之间满足的关系式,不必写出求解过程.
12.在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
(1)若点P落在矩形ABCD的边AB上(如图1).
①当点P与点A重合时,∠DEF= °,当点E与点A重合时,∠DEF= °.
②当点E在AB上时,点F在DC上时(如图2),若AP=,求四边形EPFD的周长.
(2)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图3),当AM=DE时,请求出线段AE的长度.
(3)若点P落在矩形的内部(如图4),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
13.如图1,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD且EB⊥GD;
(2)若AB=2,AG=,求的长;
(3)如图2,正方形AEFG绕点A逆时针旋转连结DE,BG,与的面积之差是否会发生变化?若不变,请求出与的面积之差;若变化,请说明理由.
14.如图.四边形ABCD、BEFG均为正方形.
(1)如图1,连接AG、CE,请直接写出AG和CE的数量和位置关系(不必证明).
(2)将正方形BEFG绕点B顺时针旋转角(),如图2,直线AG、CE相交于点M.
①AG和CE是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:
②连结MB,求证:MB平分.
(3)在(2)的条件下,过点A作交MB的延长线于点N,请直接写出线段CM与BN的数量关系.
15.图1,在正方形中,,为线段上一点,连接,过点作,交于点.将沿所在直线对折得到,延长交于点.
(1)求证:.
(2)若,求的长.
(3)如图2,延长交的延长线于点,若,记的面积为,求与之间的函数关系式.
16.如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
17.如图,在等腰中,,点E在AC上且不与点A、C重合,在的外部作等腰,使,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将绕点C逆时针旋转,当点E在线段BC上时,如图,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
若,,在图的基础上将绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
18.如图1,将纸片沿中位线折叠,使点的对称点落在边上,再将纸片分别沿等腰和等腰的底边上的高线、折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
(1)将纸片按图2的方式折叠成一个叠合矩形,则操作形成的折痕分别是线段______和______;______.
(2)纸片还可以按图3的方式折叠成一个叠合矩形,若,,求的长;
(3)如图4,梯形纸片满足,,,,.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出、的长.
19.在正方形中,,点为边上一点(不与点、重合),垂直于的一条直线分别交,,于点,,.
(1)①如图1,判断线段与之间的数量关系,并说明理由;
(2)如图2,若垂足为的中点,连接,交于点,连接,则______.
(3)若垂足在对角线上,正方形的边长为.
①如图3,若,,则______;
②如图4,连接,将沿着翻折,点落在点处,的中点为,则的最小值为______.
20.在菱形中,,是直线上一动点,以为边向右侧作等边(A,,按逆时针排列),点的位置随点的位置变化而变化.
(1)如图1,当点在线段上,且点在菱形内部或边上时,连接,则与的数量关系是________,与的位置关系是________;
(2)如图2,当点在线段上,且点在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)当点在直线上时,其他条件不变,连接,若,,请直接写出的面积.
21.如图1,点是正方形对角线的延长线上任意一点,以线段为边作一个正方形,线段和相交于点.
(1)求证:,.
(2)若,,求的长.
(3)如图2,正方形绕点逆时针旋转,连结、,与的面积之差是否会发生变化?若不变,请求出与的面积之差;若变化,请说明理由.
22.已知:正方形中,,绕点A顺时针旋转,它的两边分别交,或它们的延长线于点,当绕点A旋转到时如图,易证.
(1)当绕点A旋转到时如图,线段,和之间有怎样的数量关系?写出猜想,并加以证明.
(2)当绕点A旋转到如图的位置时,线段,和之间又有怎样的数量关系?请直接写出你的猜想.
(3)图中若,,求的面积为______.
23.(探索发现)如图①,四边形是正方形,分别在边上,且,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法,如图①,将绕点A顺时针旋转,点与点重合,得到,连接.
(1)试判断之间的数量关系,并写出证明过程;
(2)如图①如果正方形的边长为4,求三角形的周长;
(3)如图②,点分别在正方形的边的延长线上,,连接,请写出之间的数量关系,并写出证明过程.
24.已知矩形中,,是边上一点,连接,将沿着直线折叠得到.
(1)若;
①如图1,若点在边上,的长为 ;
②、、三点在同一直线上时,求的长;
(2)如图3,当点是的中点时,此时点落在矩形内部,延长交于点,若点是的三等分点,求的长.
25.在学习了正方形后,数学小组的同学对正方形进行了探究,聪明的你也加入探究吧:
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B,C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB,CD于点M,N.
此时,①∠AEB与∠AMN有什么数量关系?(直接写出即可)
②AE与MN之间又有什么数量关系?并说明理由;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD,MN与BD交于点G,连接BF,此时有结论:BF=FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB,CD于点M,N,请你继续探究线段BF与FG之间的数量关系.并证明你的结论.
26.点是线段上的动点,分别以,为边在的同侧作正方形与正方形.
(1)如图,连结、,判断与的位置关系和数量关系,并证明.
(2)如图,将正方形绕点逆时针旋转,使得点落在线段上,交于点,若,,求.
(3)如图,将方形绕点旋转至如图的位置,且,连结,作的角平分线交于点,请写出、、之间的数量关系,并证明.
答案
一、解答题
1.
(1)
①证明:由正方形的性质可知,,.
如图,过点B作于点F.
∴四边形MBFN为平行四边形,
∴MN=BF,,
∴.
∵,
∴.
∴在和中,
∴(ASA),
∴AE=BF,
∴AE=MN;
②∵,
∴,
∵E为边BC上一点(不与点、重合),
∴.
∵正方形的边长为1,
∴,,
∴,
∴;
(2)
如图,连接AF,过点F作,分别交AD,BC于点H,I,
∵四边形ABCD是正方形,
∴.
∵,
∴,
∴四边形ABIH为矩形,
∴,.
∵BD是正方形ABCD的对角线,
∴,
∴是等腰直角三角形,
∴HD=HF,AH=FI.
∵MN是AE的垂直平分线,
∴AF=FE.
∴在Rt和Rt中,
∴(HL),
∴,
∴,
∴,
∴是等腰直角三角形,
∴;
(3)
PH的长度不变,理由如下:
过点P作于点Q,于点G,延长MN,使PF=PN,连接AF、BF、AN,过点N作,交BD于点K,
∵四边形ABCD是正方形,
∴.
∵,,
∴,.
∵,
∴.
又∵,
∴(ASA),
∴.
又∵,
∴.
∵PF=PN,,
∴AF=AN,
∴,
∴,
∴.
又∵AB=AD,
∴(SAS),
∴,
∴,
∴F,B,C三点共线.
∵,
∴,,
∴DN=KN.
又∵,
∴DH=HK.
∵,
∴.
又∵,PN=PF,
∴(ASA),
∴BP=PK,
∴.
2.(1)解:连接交于点,如图所示
∵四边形是矩形,,
∴
∵、分别是、中点
∴,
∵四边形是矩形
∴
∴
当点在点上方时,
当点在点下方时,
∵速度均为每秒2个单位长度
∴ 的值为或
(2)解:①连接、,交于点,如图所示
∵四边形为菱形
∴,,,
∵,
∴
∵矩形
∴
在和中
∵
∴
∴
∴
∴直线是线段的垂直平分线
∴
设,则
在中,
∴,解得:
∴
∴的值为7
②连接、,如图所示
∵四边形的面积是矩形面积的
∴四边形的面积为:
∵是的垂直平分线
∴,
由①可得:,
由题意可得:,
∴
∴
同理可得:
∴
∴四边形是平行四边形
∴
由题意可得:
∵
∴,解得:
∴当四边形的面积是矩形面积的,则的值是,
故答案是:;
③作关于的对称点为点,连接、,过点作的垂线,交延长线于点,如图所示
由②可得:四边形是平行四边形
∴四边形周长
∵对称
∴
∴
当、、三点共线时,的值最小,即的值最小,最小值为的长度,此时四边形周长最小
∵
∴
∵=
∴四边形周长最小值为.
故答案是:.
3.(1)四边形BE′FE是正方形.
理由如下:由旋转得,∠E′=∠AEB=90°,∠EBE′=90°,
∵∠BEF=180°﹣∠AEB=90°,
∴四边形BE′FE是矩形,
由旋转得,BE′=BE,
∴四边形BE′FE是正方形.
(2)CF=FE',
证明:如图2,过点D作DG⊥AE于点G,则∠DGA=∠AEB=90°,
∵DA=DE,
∴AG=AE,
∵四边形ABCD是正方形,
∴DA=AB,∠DAB=90°,
∴∠BAE+∠DAG=90°,
∵∠ADG+∠DAG=90°,
∴∠ADG=∠BAE,
在△ADG和△BAE中
,
∴△ADG≌△BAE(AAS),
∴AG=BE;
∵四边形BE′FE是正方形,
∴BE=FE′,
∴AG=FE′,
由旋转得,AE=CE′,
∴AE=CE′,
∴FE′=AE=CE′,
∴CF=FE'.
(3)如图3,过点D作DG⊥AE于点G,
∵BE=FE′,CF=3,
∴AE=CE′=FE′+CF=FE′+3=BE+3,
∵AE2+BE2=AB2,且AB=,
∴(BE+3)2+BE2=()2,
解得,BE=9或BE=﹣12(不符合题意,舍去),
∴AE=9+3=12,
由(2)得,△ADG≌△BAE,
∴DG=AE=12,AG=BE=9,
∴GE=AE﹣AG=12﹣9=3,
∵∠DGE=90°,
∴DE===.
4.解:(1)∵点E在BC上,△PEC为等腰直角三角形,
∴PE=CE,∠PCE=45°,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴A,P,C三点共线,设正方形ABCD的边长为1,CE=x,
∴PE=x,PC=x,AC=,
∴AP=AC-PC=,BE=BC-CE=1-x,
∴AP=BE;
(2)成立,
如图,过点B作BH⊥BE,且BH=BE,连接AH,EH,
∵∠ABC=∠EBH=90°,
∴∠CBE+∠ABE=∠ABH+∠ABE=90°,
∴∠CBE=∠ABH,
又∵BH=BE,AB=BC,
∴△ABH≌△BEC(SAS),
∴AH=EC=PE,∠AHB=∠CEB,
∴∠AHE=∠AHB-∠EHB=∠CEB-45°,
∵∠HEP=360°-∠CEB-∠HEB-∠CEP
=360°-∠CEB-45°-90°
=225°-∠CEB,
∴∠AHE+∠HEP=∠CEB-45°+225°-∠CEB=180°,
∴AH∥PE,
∴四边形AHEP是平行四边形,
∴AP=EH=BE;
(3)如图,过B,D分别作AF的垂线,垂足为K,M,
∵∠BAD=∠BAK+∠DAM=90°,∠ABK+∠BAK=90°,
∴∠ABK=∠DAM,
又∵AB=AD,∠AKB=∠AMD=90°,
∴△ABK≌△DAM(AAS),
∴BK=AM,
∵四边形ABCD是正方形,DP=PC=2,
∴AD=CD=4,∠AHE=90°,
∴AP=,
∴S△ADP=,
∴,
∴,
∴AM=,
由(2)可知:△EBH为等腰直角三角形,HE∥AP,
∴∠KBF=∠HBE=45°,
∴∠F=45°,
∴BF==.
5.(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EFAB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形;
(2)解:①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,
∴CE=BC=5cm,
在RtCDE中,DE==4cm,
∴AE=AD﹣DE=5cm﹣4cm=1cm;
在RtAPE中,AE=1,AP=3﹣PB=3﹣PE,
∴EP2=12+(3﹣EP)2,
解得:EP=cm,
∴菱形BFEP的边长为cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm.
6.解:(1)∵四边形ABCD是正方形,
∴CD=AB=BC,CD∥AB.
∵AF=BE,
∴AB=EF.
∴CD=EF,CD∥EF.
∴四边形CEFD是平行四边形.
(2)①∵四边形ABCD是正方形,
∴∠EAH=45°,
∵EH⊥AC,
∴∠AHE=90°,
∴△AEH是等腰直角三角形,
∴AH=EH;
②∵△AEH是等腰直角三角形,
∴,
∵BE:AE=1:,
∴,
∴,
∵CE=CE,∠B=∠CHE=90°,
∴△BCE≌△HCE(HL),
∴∠BCE=∠HCE,
∵∠BCH=45°,
∴∠BCE=22.5°;
③由△AEH是等腰直角三角形,
∴∠EAH=∠HEA=45°,
在等腰直角△ABC中,有,
∵,
∴;
∵,
∴,
∴,
∴△ACE∽△EFH,
∴;
∴的值不变,.
7.(1)①如图,连接,
∵四边形和四边形都是正方形,
∴,,
∴,
∵为的中点,
∴,则,
在中,
,
∴,
∴,,
在中,
,
∴,
∴,
∴,
∴,
∴,
∴,
∴是等腰直角三角形,
∴;
②,
证明:如图,延长交于点,连接,
∵四边形和四边形都是正方形,
∴,,
∵落在对角线的延长线上,
∴,
∴,
∴在的延长线上,
∵,
∴,
在中,
,
∴,
∴,
∵,
∴,
∵,为的中点,
∴,
∴,
∵,
∴,
∴,
在中,
,
∴,
∴,,
∴,
∵,,
∴ ,
设,,
∴,,
∵,
∴,
即,
∴;
(2)如图,连接,
∵
∴当在上时,如图,此时最大,,
由(1)可知是等腰直角三角形,
∵,,
∴,,
∴
∴,
∴
当在上时,最小,同理可得是等腰直角三角形,
此时,
综上所述,.
8.(1)解:由题意可知,当点恰好落在边上时,点到边的距离等于F到边的距离,即DF=1,
∴点到边的距离为:1,
∵CE=1,,
∴在中,,
∵,
∴,
故答案为:1,30;
(2)证明:∵G为中点,
∴,
∴,
∵长方形绕点C顺时针旋转至,
∴,
∴,
在和中,
∵
∴,
∴;
(3)能,理由如下:
∵四边形ABCD为正方形,
∴CB=CD,
∵,
∴和为腰相等的两等腰三角形,
当时,,
当和为钝角三角形时,则旋转角=,
当和为锐角三角形时, ,
则=,
即旋转角的值为135°或315°时,和全等.
9.解:(1)如图1中,
四边形是菱形,
,
,
是等边三角形,
,
,
,
,此时点与重合,
.
(2)如图2中,连接.
是等边三角形,
,,
,,
,
,
,
.
(3)如图3中,
由翻折可知,,
,
,
,
,
,
,
,,,
,
,
,
,
,
,
,
,,
过点作交的延长线于,在上取一点,使得,连接,
,
,
设,
,
,
,
,,
,
,
,
,,
,
.
10.(1)由平移,得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
∵矩形ABCD,∴∠B=90°,∵BE=AE=,
∴AE=4,
又∵AE=AD=4,
∴四边形AEFD是菱形.
(2)由(1)得:△ABE是等腰直角三角形∴∠AEB=45°,
∵AE∥DF,
∴∠F=∠AEB=45°,
∵矩形ABCD,∴AD∥BC
∴∠DAE=∠AEB=45°,
∴∠GAE=90°,
∵△DCF绕点D旋转得到△DGA,
∴GA=CF=,
∴.
(3)PF、AQ、PQ之间的数量关系为:
PQ2=PF2+AQ2.
理由如下:
由(2)得:∠AEB=45°,∴∠ADF=∠AEF=135°,∵AD=DF,
∴将△DFP绕点D逆时针旋转135°得△DAG,
连GQ,如图,∴GA=PF,DG=DP,∠GDA=∠PDF,∠GAD=∠F=45°,
∴∠GAQ=∠GAD+∠DAE=90°,
∴GQ2=GA2+AQ2=PF2+AQ2;
又∵∠ADF=135°,而∠PDQ=67.5°,∴∠PDF+∠ADQ=135°﹣67.5°=67.5°,
∴∠GDA+∠ADQ=∠GDQ=67.5°,∴∠PDQ=∠GDQ
而DG=DP,DQ为公共边,∴△PDQ≌△GDQ,
∴PQ=GQ,
∴PQ2=PF2+AQ2.
11.解:(1)如图1中,
∵四边形ABCD是菱形,
∴BC∥AD,∠BAC=∠DAC,
∴∠ABC+∠BAD=180°,
∵∠ABC=120°,
∴∠BAD=60°,
∴∠EAF=30°,
∵AE=AF,
∴∠AEF=∠AFE=75°,
∵∠BEF=120°,
∴∠AEB=120°﹣75°=45°.
(2)①如图2中,连接DE.
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(SAS),
∴BE=DE,∠ABE=∠ADE,
∵∠BAF+∠BEF=60°+120°=180°,
∴∠ABE+∠AFE=180°,
∵∠AFE+∠EFD=180°,
∴∠EFD=∠ABE,
∴∠EFD=∠ADE,
∴EF=ED,
∴EF=BE,
∵BE∥FG,BG∥EF,
∴四边形BEFG是平行四边形,
∵EB=EF,
∴四边形BEFG是菱形,
∴当BE⊥AC时,菱形BEFG的周长最小,此时BE=AB sin30°=2,
∴四边形BGFE的周长的最小值为8.
②如图2﹣1中,连接BD,DE,过点E作EH⊥CD于H.
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴BD=BA,∠ABD=60°,
∵BG∥EF,
∴∠EBG=180°﹣120°=60°,
∴∠ABD=∠GBE,
∴∠ABG=∠DBE,
∵BG=BE,
∴△ABG≌△DBE(SAS),
∴AG=DE=y,
在Rt△CEH中,EH=EC=x.CH=x,
∴DH=|4﹣x|,
在Rt△DEH中,∵DE2=EH2+DH2,
∴y2=x2+(4﹣x)2,
∴y2=x2﹣12x+48,
∴y=(0<x<12).
12.解:(1)①当点与点重合时,
是的中垂线,
,
当点与点重合时,
此时,
故答案为:90,45.
②如图2中,设与交于点,由折叠知垂直平分.
,,
矩形,
,
,
,
,
,
,
四边形是平行四边形,
四边形是菱形,
当时,设菱形边长为,则,
在中,,
,
菱形的周长.
(2)如图3中,连接,设.
由折叠知,,,
,,
,
,
,,
在中,
解得.
.
(3)如图中,连接,,.
,,
,此时的最小值,
,
,
当与重合时,的值最小,由折叠得:,
由勾股定理得:,
,
当,,共线时,有最小值,
,
则的最小值是1.
13.(1)如图1,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠EAG=90°,∠DAB=90°,
∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
在△EAB和△GAD中,
,
∴EAB≌GAD(SAS),
∴EB=GD;∠AEB=∠AGD,
∵∠EOH=∠AOG,
∴∠EHG=∠EAG=90°,
∴EB=GD且EB⊥GD;
(2)如图2,连接BD,BD与AC交于点O,
∵AB=AD=2,
在RtABD中,,
∴AO=DO=,
∴,
∴;
(3)不变,.理由如下:
作BQ⊥GA交GA的延长线于Q,作DP⊥EA交EA于P,如图3,
正方形ABCD和正方形AEFG中,
∠EAG=∠DAB=90°,AD=AB,
∴∠EAD+∠BAG+∠EAG+∠DAB =360,则∠BAG=180°-∠EAD,
∵∠1=90°-∠EAD,∠2=∠BAG -90°=180°-∠EAD -90°=90°-∠EAD,
∴∠1=∠2,
在△PDA和△QBA中,
,
∴△PDA≌△QBA(AAS),
∴DP=BQ,
∵,,
∴.
14.解:(1)AG=EC,AG⊥EC,理由为:
∵正方形BEFG,正方形ABCD,
∴GB=BE,∠ABG=90°,AB=BC,∠ABC=90°,
在△ABG和△BEC中,
,
∴△ABG≌△BEC(SAS),
∴CE=AG,∠BCE=∠BAG,
延长CE交AG于点M,
∴∠BEC=∠AEM,
∴∠ABC=∠AME=90°,
∴AG=EC,AG⊥EC;
(2)①满足,理由是:
如图2中,设AM交BC于O.
∵∠EBG=∠ABC=90°,
∴∠ABG=∠EBC,
在△ABG和△CEB中,
,
∴△ABG≌△CEB(SAS),
∴AG=EC,∠BAG=∠BCE,
∵∠BAG+∠AOB=90°,∠AOB=∠COM,
∴∠BCE+∠COM=90°,
∴∠OMC=90°,
∴AG⊥EC.
②过B作BP⊥EC,BH⊥AM,
∵△ABG≌△CEB,
∴S△ABG=S△EBC,AG=EC,
∴EC BP=AG BH,
∴BP=BH,
∴MB平分∠AME;
(3)CM=BN,
理由为:在NA上截取NQ=NB,连接BQ,
∴△BNQ为等腰直角三角形,即BQ=BN,
∵∠AMN=45°,∠N=90°,
∴△AMN为等腰直角三角形,即AN=MN,
∴MN-BN=AN-NQ,即AQ=BM,
∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,
∴∠MBC=∠BAN,
在△ABQ和△BCM中,
,
∴△ABQ≌△BCM(SAS),
∴CM=BQ,
则CM=BN.
15.(1)在正方形ABCD中
,
,
,
,
,
,
,
.
(2)在正方形ABCD中
连接,如下图:
由折叠知BC=,
又AB=BC,∠BAN=90°
∴, ,
,
,
,
,
,
设,
,
,
,
,
.
(3)如下图,作,垂足为,
由(1)知
∵∠MBQ=∠CQB=∠MQB
∴BM=MQ
设,则.
,
,
,
故.
16.解:(1) 连接MG并延长交AB于N点,如下图所示:
∵GF∥AN,
∴∠NAM=∠GFM,
在△ANM和△FGM中,
,∴△ANM≌△FGM(ASA),
∴MG=MN,CG=GF=AN,
∴AB-AN=BC-CG,
∴NB=GB,
∴△NBG为等腰直角三角形,
又M是NG的中点,
∴由直角三角形斜边上的中线等于斜边的一半知:
故有:MG=MB.
(2)分类讨论:
情况一:当B、G、F三点在正方形ABCD外同一直线上时,
延长MG到N点,并使得MG=MN,连接AN,BN,
∴,∴△AMN≌△FMG(SAS),
∴AN=GF=GC,∠NAM=∠GFM,
∴AN∥GF,
∴∠NAB+∠ABG=180°,
又∠ABC=90°,
∴∠NAB+∠CBG=90°,
又在△BCG中,∠BCG+∠CBG=90°,
∴∠NAB=∠BCG,
∴在△ABN中和△CBG中:,∴△ABN≌△CBG(SAS),
∴BN=BG,∠ABN=∠CBG,
∴∠ABC=∠NBG=90°,
∴△NBG是等腰直角三角形,且∠BGN=45°,
在Rt△BCG中,,
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形,
∴MH=BH=HG=BG=2,
在Rt△MFH中,,
情况二:当B、G、F三点在正方形ABCD内同一直线上时,
如下图所示,延长MG到MN,并使得MG=MN,连接NA、NB,
同情况一中证明思路,
,△AMN≌△FMG(SAS),
∴AN=GF=GC,∠NAM=∠GFM,
∴AN∥GF,
∴∠NAB=∠ABG,
又∠ABG+∠GBC=90°,∠GBC+∠BIF=90°,
∴∠BIF=∠ABG,
又∠BIF=∠BCG,∠ABC=∠NAB,
∴∠NAB=∠GCB,
∴在△ABN中和△CBG中:,∴△ABN≌△CBG(SAS),
∴BN=BG,∠ABN=∠CBG,
∴∠ABC=∠NBG=90°,
∴△NBG是等腰直角三角形,且∠BGN=45°,
在△BCG中,,
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形,
∴MH=BH=HG=BG=2,
∴HF=HG-GF=2-1=1,
在Rt△MFH中,,
综上得:或
(3)由题意作出图形如下所示:
DG、MG的数量关系为:DG=MG,理由如下:
∵G点在AC上
∴∠DAG=∠BAG=45°
在△ADG和△ABG中:
,∴△ADG≌△BAG(SAS),
∴DG=BG,
又由(2)中的证明过程可知:△MBG为等腰直角三角形,
∴BG=MG,
∴DG=MG,
所以:DG=MG.
17.(1)如图①中,结论:.
理由:四边形ABFD是平行四边形,
,
,
,
,
,
,
是等腰直角三角形,
.
(2)①如图②中,结论:.
理由:连接EF,DF交BC于K.
四边形ABFD是平行四边形,
,
,
,,
,
,
,
,
,
,
在和中,
,
≌,
,,
,
是等腰直角三角形,
.
②如图③中,当时,四边形ABFD是菱形,
设AE交CD于H,
∵AC=AD,CE=DE,AE=AE,
∴△ADE≌△ACE(SSS),
∴∠DEH=∠CEH,
∵ED=EC,EH=EH,
∴△DHE≌△CHE(SAS),
∴∠EHD=∠EHC,
∴,
∴,
∴,
如图④中当时,四边形ABFD是菱形,同理可求,
综上所述,满足条件的AE的长为或.
18.解:(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
∴S矩形AEFG=S平行四边形ABCD,
∴S矩形AEFG:S平行四边形ABCD=1:2;
故答案为AE,GF,1:2;
(2)∵四边形EFGH是矩形,
∴∠HEF=90°,
∴FH==13,
由折叠的性质得:AD=FH=13;
由折叠的对称性可知:DH=NH,AH=HM,CF=FN.
易得△AEH≌CGF,
所以CF=AH,
所以AD=DH+AH=HN+FN=FH=13.
(3)有3种折法,如图4、图5、图6所示:
①折法1中,如图4所示:
由折叠的性质得:AD=BG,AE=BE=AB=4,CF=DF=CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,
∴BM=FM=4,
∴GM=CM==3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;
②折法2中,如图5所示:
由折叠的性质得:四边形EMHG的面积=梯形ABCD的面积,AE=BE=AB=4,DG=NG,NH=CH,BM=FM,MN=MC,
∴GH=CD=5,
∵四边形EMHG是叠合正方形,
∴EM=GH=5,正方形EMHG的面积=52=25,
∵∠B=90°,
∴FM=BM==3,
设AD=x,则MN=FM+FN=3+x,
∵梯形ABCD的面积=(AD+BC)×8=2×25,
∴AD+BC=,
∴BC=-x,
∴MC=BC-BM=-x-3,
∵MN=MC,
∴3+x=-x-3,
解得:x=,
∴AD=,BC=-=;
③折法3中,如图6所示,作GM⊥BC于M,
则E、G分别为AB、CD的中点,
则AH=AE=BE=BF=4,CG=CD=5,正方形的边长EF=GF=4,
GM=FM=4,CM==3,
∴BC=BF+FM+CM=11,FN=CF=7,DH=NH=8-7=1,
∴AD=5.
19.(1)∵四边形是正方形,
,,,
过点作分别交、于点、,如图所示:
四边形为平行四边形,
,
,
,
,
,
,
在和中,
,
(),
,
;
(2)连接,过点作,分别交、于点、,如图所示:
四边形是正方形,
四边形为矩形,
,,,
是正方形的对角线,
,
是等腰直角三角形,,,
是的垂直平分线,
,
在和中,
,
(),
,
,
,
是等腰直角三角形,
,
故答案为:.
(3)①解:如图所示,
过点分别作垂足分别为,则
在正方形对角线上,
,是等腰直角三角形,
,
,
又,
,
,
,
设,
,,
解得:,
则,
故答案为:.
连接交于点,如图所示:
则的直角顶点在上运动,
设点与点重合时,则点与点重合;设点与点重合时,则点的落点为,
,,
,
当点在线段上运动时,过点作于点,过点作交延长线于点,连接,
点在上,
,
在和中,
,
(),
,
,
,
,
,
,
,
,
,
,
,
,,
,,
由翻折性质得:,
在和中,
,
(),
,',
是正方形的对角线,
,
则,
,
,
,故,
点在线段上运动;
过点作,垂足为,
点为的中点,
,则的最小值为.
20.(1)解:如图,连接,延长交于H, 如图所示,
∵四边形是菱形,,
∴,都是等边三角形,,
∴,
∵是等边三角形,
∴,
∵,
∴,
∴,
∴,
∴,
同理可证是等边三角形,
∴,
∴,即,
又∵,
∴.
故答案为:;
(2)解:(1)中结论仍然成立,理由如下:
如图,连接,如图所示,
∴,为等边三角形,
在和中,,
又∵,
∴,
∴,
∴,,
设与交于点H,
同理可得,
∴,
又∵,
∴.
(3)解:如图3中,当点P在的延长线上时,连接交于点O,连接,作于F,如图所示,
∵四边形是菱形,
∴,平分,
∵,
∴,
∴,
∴,
∴,
由(2)知,
∵,,
∴,
由(2)知,
∴,
∴,
∴,
∵是等边三角形,,
∴,
∴;
如图4中,当点P在的延长线上时,
∵,,
∴,
∴,
∴,
∴;
综上所述,的面积为或.
21.(1)证明:如图1,∵四边形和是正方形,
∴∠ABC=∠EBG=900,,
∴∠ABC+∠ABE=∠EBG+∠ABE,
即,
在和中,,
∴,
∴,
∵,
∴,
∴;
(2)解:如图2,连接与交于点M,
∵,
在中,,
∴,
∴,
∴;
(3)解:与的面积之差不变,且,
如图3,过A作于P,过C作交其延长线于Q,
∵,,
∴,
∵,
∴,
在和中,,
∴,
∴,
∵,,
又,
∴,
∴.
22.(1)解:猜想:,证明如下:
如图,在的延长线上,截取,连接,
∵在和中,
∴,
,,
,,
,
,
,
∵在和中,
,
,
又,
;
(2)解:,证明如下:
如图,在上截取,连接,
∵和中,
,
,,
,
即,
,
,
∵在和中,
∴,
,
,
;
(3)解:∵,
,
的面积为:,
则的面积为.
故答案为:.
23.(1)解:,理由如下,
证明:∵是绕点A顺时针旋转 得到,
∴,,,
∵,
∴,
在与中,
∵,
∴,
∴,
∵,
∴;
(2)解:由(1)得,
;
∴,
∵正方形的边长为4,
∴;
(3)解:在上取,连接,
在与中,
∵,
∴,
∴,,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∵,
∴.
24.(1)解:四边形是矩形,
∴BC=AD=10,,,
①如图1,点在边上,
∴根据折叠有:,
∴四边形是正方形,
,
故答案为:6.
②如图2,由折叠得,,
,
,
,
,
,
的长为2.
(2)解:如图3,连接,
点是的中点,
,
由折叠得,,,
,,
在和中,
,
,
设,
点是的三等分点,
,,
,
,解得,(不符合题意,舍去),
,
的长为.
25.
(1)
解:①,②
理由如下:在图1中,过点D作PDMN交AB于P,则∠APD=∠AMN,
∵正方形ABCD,
∴ AB=AD,ABDC,∠DAB =∠B=90°,
∴四边形PMND是平行四边形,PD=MN.
∵∠B=90°,
∴∠BAE+∠BEA= 90°,
∵MN⊥AE于F,
∴∠BAE+∠AMN = 90°,
∴∠BEA=∠AMN=∠APD,
又∵AB=AD,∠B=∠DAP=90°,
∴,
∴AE=PD=MN.,∠APD=∠AMN,
∴,
(2)
解:BF=FG
理由如下:
在图2中连接AG、EG、CG,
由正方形的轴对称性得ABG△CBG,
∴AG = CG,∠GAB=∠GCB,
∵ MN⊥AE于F,F为AE中点,
∴AG=EG,
∴EG=CG,
∴∠GEC=∠GCE,
∴∠GAB=∠GEC,
由图可知∠GEB+∠GEC=180°,
∴∠GEB+∠GAB =180°,
又∵四边形ABEG的内角和为360°,∠ABE= 90°,
∴∠AGE = 90°,
在Rt△ABE 和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=AE,FG=AE,
∴BF= FG;
(3)
解:BF= FG,理由如下:
过点M作MH⊥CD于H,
∴∠MHD=∠ADC=∠DAB= 90°,
∴四边形ADHM是矩形,
∴AD=MH=AB,∠AMH= 90°,
∴∠AMF+∠HMN= 90°,
∵∠AMF+∠BAE= 90°,
∴∠BAE=∠HMN,
∴,
∴AE=MN;
连接AG、EG、CG,
由正方形的轴对称性得ABG ≌ △CBG,
∴AG = CG,∠GAB=∠GCB,
∵ MN⊥AE于F,F为AE中点,
∴ AG = EG,
∴ EG = CG,
∴∠GEC=∠GCE,
∴∠GAB=∠GEC,
∵∠GAD+∠BAG=90°,
∴∠GEC+∠GAD=90°,
∵ADBC,
∴∠DAE+∠AEB =180°,
∴∠GAE+∠AEG=90°,
∴ ∠AGE = 90°,
在Rt△ABE和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=AE,FG=AE,
∴BF= FG.
26.(1)解:,.
证明:如图,延长交于点,
在正方形和正方形中,,,,
在和中,
,
≌,
,,
,
,
;
(2)过点作于点,
,
,
,,
,
又,,
≌,
,
,,,
≌,
,,
,
,
∴EG∥PB,
,
;
(3).
证明:在上截取,连接,
正方形和正方形中,,
,,
,
≌,
,,
平分,
,
又,,
≌,
,
,
,
,
,
,
.
一、解答题
1.如图1,正方形的边长为1,为边上一点(不与点、重合),垂直于的一条直线分别交、、于点、、.
(1)①求证:;
②连接、、,直接写出四边形的面积S的取值范围.
(2)如图2,若垂足为的中点,连接,交于点,连接,求的度数.
(3)如图3,当垂足在正方形的对角线上时,作,垂足为,点在边上运动过程中,的长度是否变化?若不变,求出的长;若变化,说明变化规律.
2.在矩形中,,,、是直线上的两个动点,分别从、两点同时出发相向而行,速度均为每秒2个单位长度,运动时间为秒,其中.
(1)如图1,、分别是、中点,当四边形是矩形时,求的值.
(2)若、分别从点、沿折线,运动,与相同的速度同时出发.
①如图2,若四边形为菱形,求的值;
②如图3,作的垂直平分线交、于点、,当四边形的面积是矩形面积的,则的值是________.
③如图4,在异于、所在矩形边上取、,使得,顺次连接,请直接写出四边形周长的最小值:________.
3.如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C).延长AE交CE'于点F,连接DE.
猜想证明:
(1)四边形BE'FE的形状是______;
(2)如图②,若DA=DE,请猜想线段CF与FE的数量关系并加以证明;
(3)如图①,若AB=15,CF=3,求DE的长.
4.如图,正方形ABCD的顶点C处有一等腰直角三角形CEP,∠PEC=90°,连接AP,BE.
(1)若点E在BC上时,如图1,线段AP和BE之间的数量关系是 ;
(2)若将图1中的△CEP顺时针旋转使P点落在CD上,如图2,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在(2)的基础上延长AP,BE交于F点,若DP=PC=2,求BF的长.
5.如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EFAB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
6.如图所示,在正方形ABCD中,点E是边AB上一动点(不与A,B重合),延长BA至点F,使AF=BE,连接CE,DF.
(1) 判断四边形CEFD的形状,并说明理由;
(2) 如图①,连接AC,过点E作EH⊥AC,垂足为点H.
①证明:AH=EH;
②若BE:AE=1:,求∠BCE的度数;
③如图②,连接FH,在点E的运动过程中,的值是否发生变化?若不变,求出的值;若变化,请说明理由.
7.已知,四边形和四边形都是正方形,点为的中点.
(1)连接、.
①如图1,若点在边上,猜想和的关系,并给予证明:
②若将图1中的正方形绕点顺时针旋转,使点落在对角线的延长线上,请你在图2中补全图形,猜想和的关系,并给予证明.
(2)如图3,若,,将正方形绕点旋转,连接.请你直接写出的取值范围___________.
8.如图1所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形.现将小长方形绕点C顺时针旋转至,旋转角为.
(1)当点恰好落在边上时,点到边的距离为____________,旋转角____________;
(2)如图2,G为的中点,且,求证:;
(3)小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.
9.如图,四边形为菱形,,,点E为边上动点(不含端点)点B关于直线的对称点为点F,点H为中点.
(1)若,求的长;
(2)作,垂足为G,当时,求的度数;
(3)在(2)的条件下,设射线交于M,求的长.
10.如图1,矩形ABCD中,AB=,AD=4,在BC边上取点E,使BE=AB,将△ABE向左平移到△DCF的位置,得到四边形AEFD.
(1)求证:四边形AEFD是菱形;
(2)如图2,将△DCF绕点D旋转至△DGA,连接GE,求线段GE的长;
(3)如图3,设P、Q分别是EF、AE上的两点,且∠PDQ=67.5°,试探究线段PF、AQ、PQ之间的数量关系,并说明理由.
11.如图,在菱形ABCD中,∠ABC=120°,AB=4,E为对角线AC上的动点(点E不与A,C重合),连接BE,将射线EB绕点E逆时针旋转120°后交射线AD于点F.
(1)如图1,当AE=AF时,求∠AEB的度数;
(2)如图2,分别过点B,F作EF,BE的平行线,且两直线相交于点G.
①试探究四边形BGFE的形状,并求出四边形BGFE的周长的最小值;
②连接AG,设CE=x,AG=y,请直接写出y与x之间满足的关系式,不必写出求解过程.
12.在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
(1)若点P落在矩形ABCD的边AB上(如图1).
①当点P与点A重合时,∠DEF= °,当点E与点A重合时,∠DEF= °.
②当点E在AB上时,点F在DC上时(如图2),若AP=,求四边形EPFD的周长.
(2)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图3),当AM=DE时,请求出线段AE的长度.
(3)若点P落在矩形的内部(如图4),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
13.如图1,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD且EB⊥GD;
(2)若AB=2,AG=,求的长;
(3)如图2,正方形AEFG绕点A逆时针旋转连结DE,BG,与的面积之差是否会发生变化?若不变,请求出与的面积之差;若变化,请说明理由.
14.如图.四边形ABCD、BEFG均为正方形.
(1)如图1,连接AG、CE,请直接写出AG和CE的数量和位置关系(不必证明).
(2)将正方形BEFG绕点B顺时针旋转角(),如图2,直线AG、CE相交于点M.
①AG和CE是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:
②连结MB,求证:MB平分.
(3)在(2)的条件下,过点A作交MB的延长线于点N,请直接写出线段CM与BN的数量关系.
15.图1,在正方形中,,为线段上一点,连接,过点作,交于点.将沿所在直线对折得到,延长交于点.
(1)求证:.
(2)若,求的长.
(3)如图2,延长交的延长线于点,若,记的面积为,求与之间的函数关系式.
16.如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
17.如图,在等腰中,,点E在AC上且不与点A、C重合,在的外部作等腰,使,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将绕点C逆时针旋转,当点E在线段BC上时,如图,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
若,,在图的基础上将绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
18.如图1,将纸片沿中位线折叠,使点的对称点落在边上,再将纸片分别沿等腰和等腰的底边上的高线、折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
(1)将纸片按图2的方式折叠成一个叠合矩形,则操作形成的折痕分别是线段______和______;______.
(2)纸片还可以按图3的方式折叠成一个叠合矩形,若,,求的长;
(3)如图4,梯形纸片满足,,,,.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出、的长.
19.在正方形中,,点为边上一点(不与点、重合),垂直于的一条直线分别交,,于点,,.
(1)①如图1,判断线段与之间的数量关系,并说明理由;
(2)如图2,若垂足为的中点,连接,交于点,连接,则______.
(3)若垂足在对角线上,正方形的边长为.
①如图3,若,,则______;
②如图4,连接,将沿着翻折,点落在点处,的中点为,则的最小值为______.
20.在菱形中,,是直线上一动点,以为边向右侧作等边(A,,按逆时针排列),点的位置随点的位置变化而变化.
(1)如图1,当点在线段上,且点在菱形内部或边上时,连接,则与的数量关系是________,与的位置关系是________;
(2)如图2,当点在线段上,且点在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)当点在直线上时,其他条件不变,连接,若,,请直接写出的面积.
21.如图1,点是正方形对角线的延长线上任意一点,以线段为边作一个正方形,线段和相交于点.
(1)求证:,.
(2)若,,求的长.
(3)如图2,正方形绕点逆时针旋转,连结、,与的面积之差是否会发生变化?若不变,请求出与的面积之差;若变化,请说明理由.
22.已知:正方形中,,绕点A顺时针旋转,它的两边分别交,或它们的延长线于点,当绕点A旋转到时如图,易证.
(1)当绕点A旋转到时如图,线段,和之间有怎样的数量关系?写出猜想,并加以证明.
(2)当绕点A旋转到如图的位置时,线段,和之间又有怎样的数量关系?请直接写出你的猜想.
(3)图中若,,求的面积为______.
23.(探索发现)如图①,四边形是正方形,分别在边上,且,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法,如图①,将绕点A顺时针旋转,点与点重合,得到,连接.
(1)试判断之间的数量关系,并写出证明过程;
(2)如图①如果正方形的边长为4,求三角形的周长;
(3)如图②,点分别在正方形的边的延长线上,,连接,请写出之间的数量关系,并写出证明过程.
24.已知矩形中,,是边上一点,连接,将沿着直线折叠得到.
(1)若;
①如图1,若点在边上,的长为 ;
②、、三点在同一直线上时,求的长;
(2)如图3,当点是的中点时,此时点落在矩形内部,延长交于点,若点是的三等分点,求的长.
25.在学习了正方形后,数学小组的同学对正方形进行了探究,聪明的你也加入探究吧:
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B,C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB,CD于点M,N.
此时,①∠AEB与∠AMN有什么数量关系?(直接写出即可)
②AE与MN之间又有什么数量关系?并说明理由;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD,MN与BD交于点G,连接BF,此时有结论:BF=FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB,CD于点M,N,请你继续探究线段BF与FG之间的数量关系.并证明你的结论.
26.点是线段上的动点,分别以,为边在的同侧作正方形与正方形.
(1)如图,连结、,判断与的位置关系和数量关系,并证明.
(2)如图,将正方形绕点逆时针旋转,使得点落在线段上,交于点,若,,求.
(3)如图,将方形绕点旋转至如图的位置,且,连结,作的角平分线交于点,请写出、、之间的数量关系,并证明.
答案
一、解答题
1.
(1)
①证明:由正方形的性质可知,,.
如图,过点B作于点F.
∴四边形MBFN为平行四边形,
∴MN=BF,,
∴.
∵,
∴.
∴在和中,
∴(ASA),
∴AE=BF,
∴AE=MN;
②∵,
∴,
∵E为边BC上一点(不与点、重合),
∴.
∵正方形的边长为1,
∴,,
∴,
∴;
(2)
如图,连接AF,过点F作,分别交AD,BC于点H,I,
∵四边形ABCD是正方形,
∴.
∵,
∴,
∴四边形ABIH为矩形,
∴,.
∵BD是正方形ABCD的对角线,
∴,
∴是等腰直角三角形,
∴HD=HF,AH=FI.
∵MN是AE的垂直平分线,
∴AF=FE.
∴在Rt和Rt中,
∴(HL),
∴,
∴,
∴,
∴是等腰直角三角形,
∴;
(3)
PH的长度不变,理由如下:
过点P作于点Q,于点G,延长MN,使PF=PN,连接AF、BF、AN,过点N作,交BD于点K,
∵四边形ABCD是正方形,
∴.
∵,,
∴,.
∵,
∴.
又∵,
∴(ASA),
∴.
又∵,
∴.
∵PF=PN,,
∴AF=AN,
∴,
∴,
∴.
又∵AB=AD,
∴(SAS),
∴,
∴,
∴F,B,C三点共线.
∵,
∴,,
∴DN=KN.
又∵,
∴DH=HK.
∵,
∴.
又∵,PN=PF,
∴(ASA),
∴BP=PK,
∴.
2.(1)解:连接交于点,如图所示
∵四边形是矩形,,
∴
∵、分别是、中点
∴,
∵四边形是矩形
∴
∴
当点在点上方时,
当点在点下方时,
∵速度均为每秒2个单位长度
∴ 的值为或
(2)解:①连接、,交于点,如图所示
∵四边形为菱形
∴,,,
∵,
∴
∵矩形
∴
在和中
∵
∴
∴
∴
∴直线是线段的垂直平分线
∴
设,则
在中,
∴,解得:
∴
∴的值为7
②连接、,如图所示
∵四边形的面积是矩形面积的
∴四边形的面积为:
∵是的垂直平分线
∴,
由①可得:,
由题意可得:,
∴
∴
同理可得:
∴
∴四边形是平行四边形
∴
由题意可得:
∵
∴,解得:
∴当四边形的面积是矩形面积的,则的值是,
故答案是:;
③作关于的对称点为点,连接、,过点作的垂线,交延长线于点,如图所示
由②可得:四边形是平行四边形
∴四边形周长
∵对称
∴
∴
当、、三点共线时,的值最小,即的值最小,最小值为的长度,此时四边形周长最小
∵
∴
∵=
∴四边形周长最小值为.
故答案是:.
3.(1)四边形BE′FE是正方形.
理由如下:由旋转得,∠E′=∠AEB=90°,∠EBE′=90°,
∵∠BEF=180°﹣∠AEB=90°,
∴四边形BE′FE是矩形,
由旋转得,BE′=BE,
∴四边形BE′FE是正方形.
(2)CF=FE',
证明:如图2,过点D作DG⊥AE于点G,则∠DGA=∠AEB=90°,
∵DA=DE,
∴AG=AE,
∵四边形ABCD是正方形,
∴DA=AB,∠DAB=90°,
∴∠BAE+∠DAG=90°,
∵∠ADG+∠DAG=90°,
∴∠ADG=∠BAE,
在△ADG和△BAE中
,
∴△ADG≌△BAE(AAS),
∴AG=BE;
∵四边形BE′FE是正方形,
∴BE=FE′,
∴AG=FE′,
由旋转得,AE=CE′,
∴AE=CE′,
∴FE′=AE=CE′,
∴CF=FE'.
(3)如图3,过点D作DG⊥AE于点G,
∵BE=FE′,CF=3,
∴AE=CE′=FE′+CF=FE′+3=BE+3,
∵AE2+BE2=AB2,且AB=,
∴(BE+3)2+BE2=()2,
解得,BE=9或BE=﹣12(不符合题意,舍去),
∴AE=9+3=12,
由(2)得,△ADG≌△BAE,
∴DG=AE=12,AG=BE=9,
∴GE=AE﹣AG=12﹣9=3,
∵∠DGE=90°,
∴DE===.
4.解:(1)∵点E在BC上,△PEC为等腰直角三角形,
∴PE=CE,∠PCE=45°,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴A,P,C三点共线,设正方形ABCD的边长为1,CE=x,
∴PE=x,PC=x,AC=,
∴AP=AC-PC=,BE=BC-CE=1-x,
∴AP=BE;
(2)成立,
如图,过点B作BH⊥BE,且BH=BE,连接AH,EH,
∵∠ABC=∠EBH=90°,
∴∠CBE+∠ABE=∠ABH+∠ABE=90°,
∴∠CBE=∠ABH,
又∵BH=BE,AB=BC,
∴△ABH≌△BEC(SAS),
∴AH=EC=PE,∠AHB=∠CEB,
∴∠AHE=∠AHB-∠EHB=∠CEB-45°,
∵∠HEP=360°-∠CEB-∠HEB-∠CEP
=360°-∠CEB-45°-90°
=225°-∠CEB,
∴∠AHE+∠HEP=∠CEB-45°+225°-∠CEB=180°,
∴AH∥PE,
∴四边形AHEP是平行四边形,
∴AP=EH=BE;
(3)如图,过B,D分别作AF的垂线,垂足为K,M,
∵∠BAD=∠BAK+∠DAM=90°,∠ABK+∠BAK=90°,
∴∠ABK=∠DAM,
又∵AB=AD,∠AKB=∠AMD=90°,
∴△ABK≌△DAM(AAS),
∴BK=AM,
∵四边形ABCD是正方形,DP=PC=2,
∴AD=CD=4,∠AHE=90°,
∴AP=,
∴S△ADP=,
∴,
∴,
∴AM=,
由(2)可知:△EBH为等腰直角三角形,HE∥AP,
∴∠KBF=∠HBE=45°,
∴∠F=45°,
∴BF==.
5.(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EFAB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形;
(2)解:①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,
∴CE=BC=5cm,
在RtCDE中,DE==4cm,
∴AE=AD﹣DE=5cm﹣4cm=1cm;
在RtAPE中,AE=1,AP=3﹣PB=3﹣PE,
∴EP2=12+(3﹣EP)2,
解得:EP=cm,
∴菱形BFEP的边长为cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm.
6.解:(1)∵四边形ABCD是正方形,
∴CD=AB=BC,CD∥AB.
∵AF=BE,
∴AB=EF.
∴CD=EF,CD∥EF.
∴四边形CEFD是平行四边形.
(2)①∵四边形ABCD是正方形,
∴∠EAH=45°,
∵EH⊥AC,
∴∠AHE=90°,
∴△AEH是等腰直角三角形,
∴AH=EH;
②∵△AEH是等腰直角三角形,
∴,
∵BE:AE=1:,
∴,
∴,
∵CE=CE,∠B=∠CHE=90°,
∴△BCE≌△HCE(HL),
∴∠BCE=∠HCE,
∵∠BCH=45°,
∴∠BCE=22.5°;
③由△AEH是等腰直角三角形,
∴∠EAH=∠HEA=45°,
在等腰直角△ABC中,有,
∵,
∴;
∵,
∴,
∴,
∴△ACE∽△EFH,
∴;
∴的值不变,.
7.(1)①如图,连接,
∵四边形和四边形都是正方形,
∴,,
∴,
∵为的中点,
∴,则,
在中,
,
∴,
∴,,
在中,
,
∴,
∴,
∴,
∴,
∴,
∴,
∴是等腰直角三角形,
∴;
②,
证明:如图,延长交于点,连接,
∵四边形和四边形都是正方形,
∴,,
∵落在对角线的延长线上,
∴,
∴,
∴在的延长线上,
∵,
∴,
在中,
,
∴,
∴,
∵,
∴,
∵,为的中点,
∴,
∴,
∵,
∴,
∴,
在中,
,
∴,
∴,,
∴,
∵,,
∴ ,
设,,
∴,,
∵,
∴,
即,
∴;
(2)如图,连接,
∵
∴当在上时,如图,此时最大,,
由(1)可知是等腰直角三角形,
∵,,
∴,,
∴
∴,
∴
当在上时,最小,同理可得是等腰直角三角形,
此时,
综上所述,.
8.(1)解:由题意可知,当点恰好落在边上时,点到边的距离等于F到边的距离,即DF=1,
∴点到边的距离为:1,
∵CE=1,,
∴在中,,
∵,
∴,
故答案为:1,30;
(2)证明:∵G为中点,
∴,
∴,
∵长方形绕点C顺时针旋转至,
∴,
∴,
在和中,
∵
∴,
∴;
(3)能,理由如下:
∵四边形ABCD为正方形,
∴CB=CD,
∵,
∴和为腰相等的两等腰三角形,
当时,,
当和为钝角三角形时,则旋转角=,
当和为锐角三角形时, ,
则=,
即旋转角的值为135°或315°时,和全等.
9.解:(1)如图1中,
四边形是菱形,
,
,
是等边三角形,
,
,
,
,此时点与重合,
.
(2)如图2中,连接.
是等边三角形,
,,
,,
,
,
,
.
(3)如图3中,
由翻折可知,,
,
,
,
,
,
,
,,,
,
,
,
,
,
,
,
,,
过点作交的延长线于,在上取一点,使得,连接,
,
,
设,
,
,
,
,,
,
,
,
,,
,
.
10.(1)由平移,得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
∵矩形ABCD,∴∠B=90°,∵BE=AE=,
∴AE=4,
又∵AE=AD=4,
∴四边形AEFD是菱形.
(2)由(1)得:△ABE是等腰直角三角形∴∠AEB=45°,
∵AE∥DF,
∴∠F=∠AEB=45°,
∵矩形ABCD,∴AD∥BC
∴∠DAE=∠AEB=45°,
∴∠GAE=90°,
∵△DCF绕点D旋转得到△DGA,
∴GA=CF=,
∴.
(3)PF、AQ、PQ之间的数量关系为:
PQ2=PF2+AQ2.
理由如下:
由(2)得:∠AEB=45°,∴∠ADF=∠AEF=135°,∵AD=DF,
∴将△DFP绕点D逆时针旋转135°得△DAG,
连GQ,如图,∴GA=PF,DG=DP,∠GDA=∠PDF,∠GAD=∠F=45°,
∴∠GAQ=∠GAD+∠DAE=90°,
∴GQ2=GA2+AQ2=PF2+AQ2;
又∵∠ADF=135°,而∠PDQ=67.5°,∴∠PDF+∠ADQ=135°﹣67.5°=67.5°,
∴∠GDA+∠ADQ=∠GDQ=67.5°,∴∠PDQ=∠GDQ
而DG=DP,DQ为公共边,∴△PDQ≌△GDQ,
∴PQ=GQ,
∴PQ2=PF2+AQ2.
11.解:(1)如图1中,
∵四边形ABCD是菱形,
∴BC∥AD,∠BAC=∠DAC,
∴∠ABC+∠BAD=180°,
∵∠ABC=120°,
∴∠BAD=60°,
∴∠EAF=30°,
∵AE=AF,
∴∠AEF=∠AFE=75°,
∵∠BEF=120°,
∴∠AEB=120°﹣75°=45°.
(2)①如图2中,连接DE.
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(SAS),
∴BE=DE,∠ABE=∠ADE,
∵∠BAF+∠BEF=60°+120°=180°,
∴∠ABE+∠AFE=180°,
∵∠AFE+∠EFD=180°,
∴∠EFD=∠ABE,
∴∠EFD=∠ADE,
∴EF=ED,
∴EF=BE,
∵BE∥FG,BG∥EF,
∴四边形BEFG是平行四边形,
∵EB=EF,
∴四边形BEFG是菱形,
∴当BE⊥AC时,菱形BEFG的周长最小,此时BE=AB sin30°=2,
∴四边形BGFE的周长的最小值为8.
②如图2﹣1中,连接BD,DE,过点E作EH⊥CD于H.
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴BD=BA,∠ABD=60°,
∵BG∥EF,
∴∠EBG=180°﹣120°=60°,
∴∠ABD=∠GBE,
∴∠ABG=∠DBE,
∵BG=BE,
∴△ABG≌△DBE(SAS),
∴AG=DE=y,
在Rt△CEH中,EH=EC=x.CH=x,
∴DH=|4﹣x|,
在Rt△DEH中,∵DE2=EH2+DH2,
∴y2=x2+(4﹣x)2,
∴y2=x2﹣12x+48,
∴y=(0<x<12).
12.解:(1)①当点与点重合时,
是的中垂线,
,
当点与点重合时,
此时,
故答案为:90,45.
②如图2中,设与交于点,由折叠知垂直平分.
,,
矩形,
,
,
,
,
,
,
四边形是平行四边形,
四边形是菱形,
当时,设菱形边长为,则,
在中,,
,
菱形的周长.
(2)如图3中,连接,设.
由折叠知,,,
,,
,
,
,,
在中,
解得.
.
(3)如图中,连接,,.
,,
,此时的最小值,
,
,
当与重合时,的值最小,由折叠得:,
由勾股定理得:,
,
当,,共线时,有最小值,
,
则的最小值是1.
13.(1)如图1,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠EAG=90°,∠DAB=90°,
∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
在△EAB和△GAD中,
,
∴EAB≌GAD(SAS),
∴EB=GD;∠AEB=∠AGD,
∵∠EOH=∠AOG,
∴∠EHG=∠EAG=90°,
∴EB=GD且EB⊥GD;
(2)如图2,连接BD,BD与AC交于点O,
∵AB=AD=2,
在RtABD中,,
∴AO=DO=,
∴,
∴;
(3)不变,.理由如下:
作BQ⊥GA交GA的延长线于Q,作DP⊥EA交EA于P,如图3,
正方形ABCD和正方形AEFG中,
∠EAG=∠DAB=90°,AD=AB,
∴∠EAD+∠BAG+∠EAG+∠DAB =360,则∠BAG=180°-∠EAD,
∵∠1=90°-∠EAD,∠2=∠BAG -90°=180°-∠EAD -90°=90°-∠EAD,
∴∠1=∠2,
在△PDA和△QBA中,
,
∴△PDA≌△QBA(AAS),
∴DP=BQ,
∵,,
∴.
14.解:(1)AG=EC,AG⊥EC,理由为:
∵正方形BEFG,正方形ABCD,
∴GB=BE,∠ABG=90°,AB=BC,∠ABC=90°,
在△ABG和△BEC中,
,
∴△ABG≌△BEC(SAS),
∴CE=AG,∠BCE=∠BAG,
延长CE交AG于点M,
∴∠BEC=∠AEM,
∴∠ABC=∠AME=90°,
∴AG=EC,AG⊥EC;
(2)①满足,理由是:
如图2中,设AM交BC于O.
∵∠EBG=∠ABC=90°,
∴∠ABG=∠EBC,
在△ABG和△CEB中,
,
∴△ABG≌△CEB(SAS),
∴AG=EC,∠BAG=∠BCE,
∵∠BAG+∠AOB=90°,∠AOB=∠COM,
∴∠BCE+∠COM=90°,
∴∠OMC=90°,
∴AG⊥EC.
②过B作BP⊥EC,BH⊥AM,
∵△ABG≌△CEB,
∴S△ABG=S△EBC,AG=EC,
∴EC BP=AG BH,
∴BP=BH,
∴MB平分∠AME;
(3)CM=BN,
理由为:在NA上截取NQ=NB,连接BQ,
∴△BNQ为等腰直角三角形,即BQ=BN,
∵∠AMN=45°,∠N=90°,
∴△AMN为等腰直角三角形,即AN=MN,
∴MN-BN=AN-NQ,即AQ=BM,
∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,
∴∠MBC=∠BAN,
在△ABQ和△BCM中,
,
∴△ABQ≌△BCM(SAS),
∴CM=BQ,
则CM=BN.
15.(1)在正方形ABCD中
,
,
,
,
,
,
,
.
(2)在正方形ABCD中
连接,如下图:
由折叠知BC=,
又AB=BC,∠BAN=90°
∴, ,
,
,
,
,
,
设,
,
,
,
,
.
(3)如下图,作,垂足为,
由(1)知
∵∠MBQ=∠CQB=∠MQB
∴BM=MQ
设,则.
,
,
,
故.
16.解:(1) 连接MG并延长交AB于N点,如下图所示:
∵GF∥AN,
∴∠NAM=∠GFM,
在△ANM和△FGM中,
,∴△ANM≌△FGM(ASA),
∴MG=MN,CG=GF=AN,
∴AB-AN=BC-CG,
∴NB=GB,
∴△NBG为等腰直角三角形,
又M是NG的中点,
∴由直角三角形斜边上的中线等于斜边的一半知:
故有:MG=MB.
(2)分类讨论:
情况一:当B、G、F三点在正方形ABCD外同一直线上时,
延长MG到N点,并使得MG=MN,连接AN,BN,
∴,∴△AMN≌△FMG(SAS),
∴AN=GF=GC,∠NAM=∠GFM,
∴AN∥GF,
∴∠NAB+∠ABG=180°,
又∠ABC=90°,
∴∠NAB+∠CBG=90°,
又在△BCG中,∠BCG+∠CBG=90°,
∴∠NAB=∠BCG,
∴在△ABN中和△CBG中:,∴△ABN≌△CBG(SAS),
∴BN=BG,∠ABN=∠CBG,
∴∠ABC=∠NBG=90°,
∴△NBG是等腰直角三角形,且∠BGN=45°,
在Rt△BCG中,,
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形,
∴MH=BH=HG=BG=2,
在Rt△MFH中,,
情况二:当B、G、F三点在正方形ABCD内同一直线上时,
如下图所示,延长MG到MN,并使得MG=MN,连接NA、NB,
同情况一中证明思路,
,△AMN≌△FMG(SAS),
∴AN=GF=GC,∠NAM=∠GFM,
∴AN∥GF,
∴∠NAB=∠ABG,
又∠ABG+∠GBC=90°,∠GBC+∠BIF=90°,
∴∠BIF=∠ABG,
又∠BIF=∠BCG,∠ABC=∠NAB,
∴∠NAB=∠GCB,
∴在△ABN中和△CBG中:,∴△ABN≌△CBG(SAS),
∴BN=BG,∠ABN=∠CBG,
∴∠ABC=∠NBG=90°,
∴△NBG是等腰直角三角形,且∠BGN=45°,
在△BCG中,,
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形,
∴MH=BH=HG=BG=2,
∴HF=HG-GF=2-1=1,
在Rt△MFH中,,
综上得:或
(3)由题意作出图形如下所示:
DG、MG的数量关系为:DG=MG,理由如下:
∵G点在AC上
∴∠DAG=∠BAG=45°
在△ADG和△ABG中:
,∴△ADG≌△BAG(SAS),
∴DG=BG,
又由(2)中的证明过程可知:△MBG为等腰直角三角形,
∴BG=MG,
∴DG=MG,
所以:DG=MG.
17.(1)如图①中,结论:.
理由:四边形ABFD是平行四边形,
,
,
,
,
,
,
是等腰直角三角形,
.
(2)①如图②中,结论:.
理由:连接EF,DF交BC于K.
四边形ABFD是平行四边形,
,
,
,,
,
,
,
,
,
,
在和中,
,
≌,
,,
,
是等腰直角三角形,
.
②如图③中,当时,四边形ABFD是菱形,
设AE交CD于H,
∵AC=AD,CE=DE,AE=AE,
∴△ADE≌△ACE(SSS),
∴∠DEH=∠CEH,
∵ED=EC,EH=EH,
∴△DHE≌△CHE(SAS),
∴∠EHD=∠EHC,
∴,
∴,
∴,
如图④中当时,四边形ABFD是菱形,同理可求,
综上所述,满足条件的AE的长为或.
18.解:(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
∴S矩形AEFG=S平行四边形ABCD,
∴S矩形AEFG:S平行四边形ABCD=1:2;
故答案为AE,GF,1:2;
(2)∵四边形EFGH是矩形,
∴∠HEF=90°,
∴FH==13,
由折叠的性质得:AD=FH=13;
由折叠的对称性可知:DH=NH,AH=HM,CF=FN.
易得△AEH≌CGF,
所以CF=AH,
所以AD=DH+AH=HN+FN=FH=13.
(3)有3种折法,如图4、图5、图6所示:
①折法1中,如图4所示:
由折叠的性质得:AD=BG,AE=BE=AB=4,CF=DF=CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,
∴BM=FM=4,
∴GM=CM==3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;
②折法2中,如图5所示:
由折叠的性质得:四边形EMHG的面积=梯形ABCD的面积,AE=BE=AB=4,DG=NG,NH=CH,BM=FM,MN=MC,
∴GH=CD=5,
∵四边形EMHG是叠合正方形,
∴EM=GH=5,正方形EMHG的面积=52=25,
∵∠B=90°,
∴FM=BM==3,
设AD=x,则MN=FM+FN=3+x,
∵梯形ABCD的面积=(AD+BC)×8=2×25,
∴AD+BC=,
∴BC=-x,
∴MC=BC-BM=-x-3,
∵MN=MC,
∴3+x=-x-3,
解得:x=,
∴AD=,BC=-=;
③折法3中,如图6所示,作GM⊥BC于M,
则E、G分别为AB、CD的中点,
则AH=AE=BE=BF=4,CG=CD=5,正方形的边长EF=GF=4,
GM=FM=4,CM==3,
∴BC=BF+FM+CM=11,FN=CF=7,DH=NH=8-7=1,
∴AD=5.
19.(1)∵四边形是正方形,
,,,
过点作分别交、于点、,如图所示:
四边形为平行四边形,
,
,
,
,
,
,
在和中,
,
(),
,
;
(2)连接,过点作,分别交、于点、,如图所示:
四边形是正方形,
四边形为矩形,
,,,
是正方形的对角线,
,
是等腰直角三角形,,,
是的垂直平分线,
,
在和中,
,
(),
,
,
,
是等腰直角三角形,
,
故答案为:.
(3)①解:如图所示,
过点分别作垂足分别为,则
在正方形对角线上,
,是等腰直角三角形,
,
,
又,
,
,
,
设,
,,
解得:,
则,
故答案为:.
连接交于点,如图所示:
则的直角顶点在上运动,
设点与点重合时,则点与点重合;设点与点重合时,则点的落点为,
,,
,
当点在线段上运动时,过点作于点,过点作交延长线于点,连接,
点在上,
,
在和中,
,
(),
,
,
,
,
,
,
,
,
,
,
,
,,
,,
由翻折性质得:,
在和中,
,
(),
,',
是正方形的对角线,
,
则,
,
,
,故,
点在线段上运动;
过点作,垂足为,
点为的中点,
,则的最小值为.
20.(1)解:如图,连接,延长交于H, 如图所示,
∵四边形是菱形,,
∴,都是等边三角形,,
∴,
∵是等边三角形,
∴,
∵,
∴,
∴,
∴,
∴,
同理可证是等边三角形,
∴,
∴,即,
又∵,
∴.
故答案为:;
(2)解:(1)中结论仍然成立,理由如下:
如图,连接,如图所示,
∴,为等边三角形,
在和中,,
又∵,
∴,
∴,
∴,,
设与交于点H,
同理可得,
∴,
又∵,
∴.
(3)解:如图3中,当点P在的延长线上时,连接交于点O,连接,作于F,如图所示,
∵四边形是菱形,
∴,平分,
∵,
∴,
∴,
∴,
∴,
由(2)知,
∵,,
∴,
由(2)知,
∴,
∴,
∴,
∵是等边三角形,,
∴,
∴;
如图4中,当点P在的延长线上时,
∵,,
∴,
∴,
∴,
∴;
综上所述,的面积为或.
21.(1)证明:如图1,∵四边形和是正方形,
∴∠ABC=∠EBG=900,,
∴∠ABC+∠ABE=∠EBG+∠ABE,
即,
在和中,,
∴,
∴,
∵,
∴,
∴;
(2)解:如图2,连接与交于点M,
∵,
在中,,
∴,
∴,
∴;
(3)解:与的面积之差不变,且,
如图3,过A作于P,过C作交其延长线于Q,
∵,,
∴,
∵,
∴,
在和中,,
∴,
∴,
∵,,
又,
∴,
∴.
22.(1)解:猜想:,证明如下:
如图,在的延长线上,截取,连接,
∵在和中,
∴,
,,
,,
,
,
,
∵在和中,
,
,
又,
;
(2)解:,证明如下:
如图,在上截取,连接,
∵和中,
,
,,
,
即,
,
,
∵在和中,
∴,
,
,
;
(3)解:∵,
,
的面积为:,
则的面积为.
故答案为:.
23.(1)解:,理由如下,
证明:∵是绕点A顺时针旋转 得到,
∴,,,
∵,
∴,
在与中,
∵,
∴,
∴,
∵,
∴;
(2)解:由(1)得,
;
∴,
∵正方形的边长为4,
∴;
(3)解:在上取,连接,
在与中,
∵,
∴,
∴,,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∵,
∴.
24.(1)解:四边形是矩形,
∴BC=AD=10,,,
①如图1,点在边上,
∴根据折叠有:,
∴四边形是正方形,
,
故答案为:6.
②如图2,由折叠得,,
,
,
,
,
,
的长为2.
(2)解:如图3,连接,
点是的中点,
,
由折叠得,,,
,,
在和中,
,
,
设,
点是的三等分点,
,,
,
,解得,(不符合题意,舍去),
,
的长为.
25.
(1)
解:①,②
理由如下:在图1中,过点D作PDMN交AB于P,则∠APD=∠AMN,
∵正方形ABCD,
∴ AB=AD,ABDC,∠DAB =∠B=90°,
∴四边形PMND是平行四边形,PD=MN.
∵∠B=90°,
∴∠BAE+∠BEA= 90°,
∵MN⊥AE于F,
∴∠BAE+∠AMN = 90°,
∴∠BEA=∠AMN=∠APD,
又∵AB=AD,∠B=∠DAP=90°,
∴,
∴AE=PD=MN.,∠APD=∠AMN,
∴,
(2)
解:BF=FG
理由如下:
在图2中连接AG、EG、CG,
由正方形的轴对称性得ABG△CBG,
∴AG = CG,∠GAB=∠GCB,
∵ MN⊥AE于F,F为AE中点,
∴AG=EG,
∴EG=CG,
∴∠GEC=∠GCE,
∴∠GAB=∠GEC,
由图可知∠GEB+∠GEC=180°,
∴∠GEB+∠GAB =180°,
又∵四边形ABEG的内角和为360°,∠ABE= 90°,
∴∠AGE = 90°,
在Rt△ABE 和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=AE,FG=AE,
∴BF= FG;
(3)
解:BF= FG,理由如下:
过点M作MH⊥CD于H,
∴∠MHD=∠ADC=∠DAB= 90°,
∴四边形ADHM是矩形,
∴AD=MH=AB,∠AMH= 90°,
∴∠AMF+∠HMN= 90°,
∵∠AMF+∠BAE= 90°,
∴∠BAE=∠HMN,
∴,
∴AE=MN;
连接AG、EG、CG,
由正方形的轴对称性得ABG ≌ △CBG,
∴AG = CG,∠GAB=∠GCB,
∵ MN⊥AE于F,F为AE中点,
∴ AG = EG,
∴ EG = CG,
∴∠GEC=∠GCE,
∴∠GAB=∠GEC,
∵∠GAD+∠BAG=90°,
∴∠GEC+∠GAD=90°,
∵ADBC,
∴∠DAE+∠AEB =180°,
∴∠GAE+∠AEG=90°,
∴ ∠AGE = 90°,
在Rt△ABE和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=AE,FG=AE,
∴BF= FG.
26.(1)解:,.
证明:如图,延长交于点,
在正方形和正方形中,,,,
在和中,
,
≌,
,,
,
,
;
(2)过点作于点,
,
,
,,
,
又,,
≌,
,
,,,
≌,
,,
,
,
∴EG∥PB,
,
;
(3).
证明:在上截取,连接,
正方形和正方形中,,
,,
,
≌,
,,
平分,
,
又,,
≌,
,
,
,
,
,
,
.
