北师大版数学七下 期中考试题型总结(无答案)
文档属性
| 名称 | 北师大版数学七下 期中考试题型总结(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 584.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 17:35:42 | ||
图片预览


文档简介
期中考试题型总结
1.下列运算正确的是( )
A. B. C. D.
2.今年肆虐全球的新冠肺炎(COVID﹣19)被世界卫生组织(WHO)标识为“全球大流行病”,它给全球人民带来了巨大的灾难.冠状病毒的直径约80﹣120nm,1nm为十亿分之一米,即10﹣9m.将120nm用科学记数法表示正确的是( )米.
A.1.2×10﹣7 B.1.2×10﹣8 C.120×10﹣9 D.12×10﹣8
3a.下列多项式乘法中可以用平方差公式计算的是( )
A. B. C. D.
3b.下列多项式乘法中不能用平方差公式计算的是( )
B. C. D.
4a.下列命题中,真命题的个数是( )
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;②两条直线被第三条直线所截,同旁内角互补;③两直线平行,内错角相等;④同一平面内,过一点有且只有一条直线与已知直线垂直;⑤从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
A.1个 B.2个 C.3个 D.4个
4b.下列四个命题中,正确的是( )
A.经过直线外一点,有且只有一条直线与这条直线平行
B.同旁内角相等,两直线平行
C.相等的角是对顶角
D.若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补
5a.下列图形中,线段PQ的长度表示点P到直线a的距离的是( )
5b.如图,,,垂足为D,,,,则点A到直线的距离为( )
A.5 B.4 C.3 D.
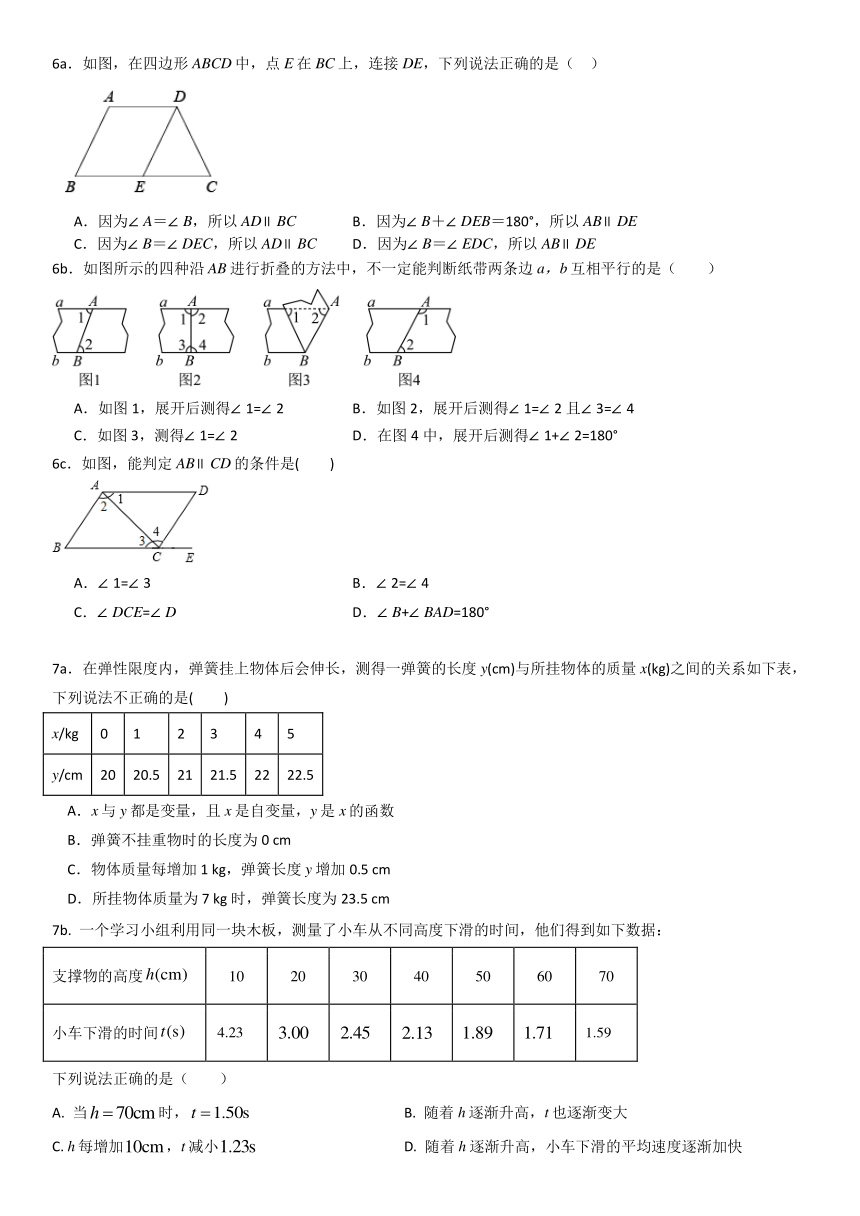
6a.如图,在四边形ABCD中,点E在BC上,连接DE,下列说法正确的是( )
A.因为∠A=∠B,所以AD∥BC B.因为∠B+∠DEB=180°,所以AB∥DE
C.因为∠B=∠DEC,所以AD∥BC D.因为∠B=∠EDC,所以AB∥DE
6b.如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2 B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2 D.在图4中,展开后测得∠1+∠2=180°
6c.如图,能判定AB∥CD的条件是( )
A.∠1=∠3 B.∠2=∠4
C.∠DCE=∠D D.∠B+∠BAD=180°
7a.在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg 0 1 2 3 4 5
y/cm 20 20.5 21 21.5 22 22.5
A.x与y都是变量,且x是自变量,y是x的函数
B.弹簧不挂重物时的长度为0 cm
C.物体质量每增加1 kg,弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时,弹簧长度为23.5 cm
7b. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
支撑物的高度 10 20 30 40 50 60 70
小车下滑的时间
下列说法正确的是( )
A. 当时, B. 随着h逐渐升高,t也逐渐变大
C. h每增加,t减小 D. 随着h逐渐升高,小车下滑的平均速度逐渐加快
7c.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量(升)与行驶时间(小时)之间的函数关系的图象是( )
A. B. C. D.
7d.如图,在长方形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则长方形ABCD的周长是( )
A.24 B.18 C.20 D.40
8a.如图将4个长、宽分别均为,的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
A. B.
C. D.
8b.边长分别为a和b(其中)的两个正方形按下图摆放,如果,,则图中阴影部分的面积为( )
A.25 B. C.13 D.
9a.已知,则 .
9b.已知:,,的值为 .
9c.已知a+2b-2=0,则3a×9b=_________.
10a若是一个完全平方式,则m的值为
10b.若多项式4a2-ka+16是一个完全平方式,则k=_________
10c若x2 +2mx + 16是关于x的完全平方式,则m= .
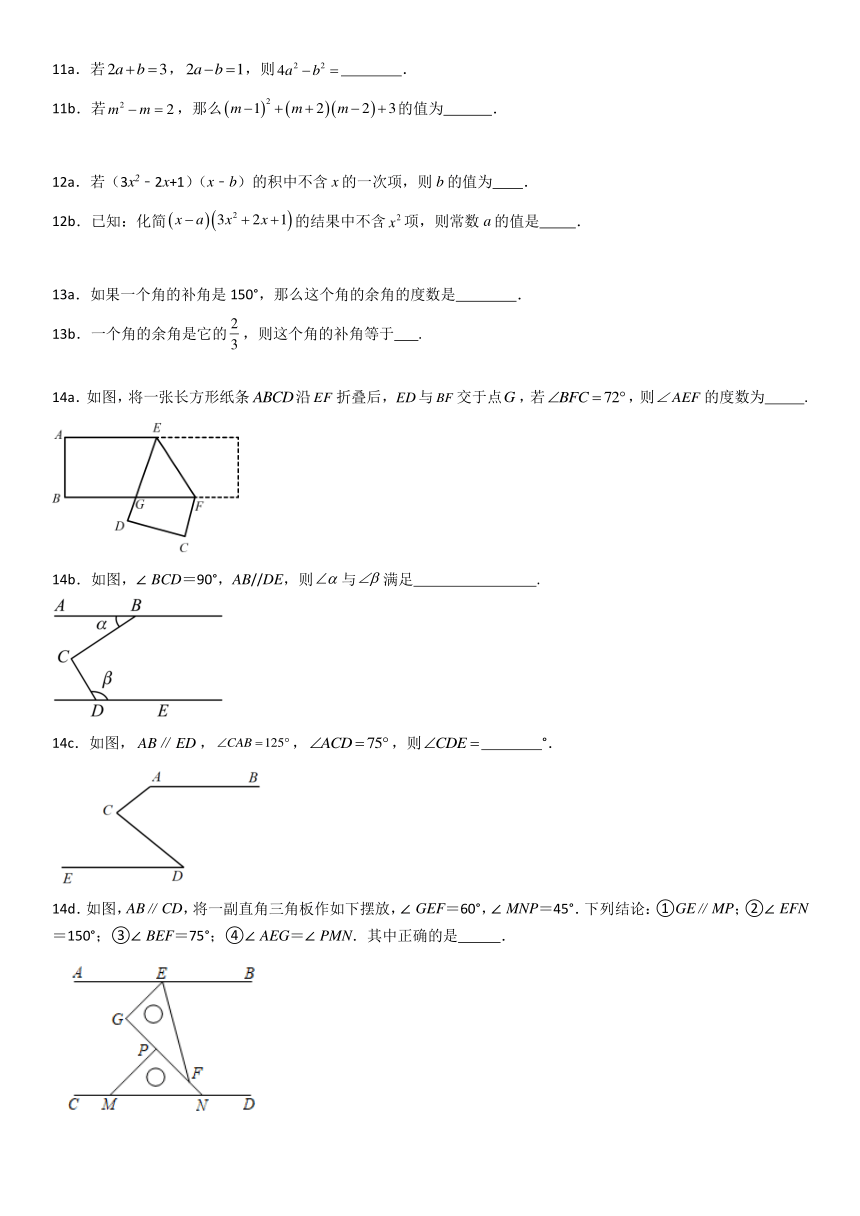
11a.若,,则 .
11b.若,那么的值为 .
12a.若(3x2﹣2x+1)(x﹣b)的积中不含x的一次项,则b的值为 .
12b.已知:化简的结果中不含项,则常数a的值是 .
13a.如果一个角的补角是150°,那么这个角的余角的度数是 .
13b.一个角的余角是它的,则这个角的补角等于 .
14a.如图,将一张长方形纸条沿折叠后,与交于点,若,则的度数为 .
14b.如图,∠BCD=90°,AB//DE,则与满足 .
14c.如图,,,,则 °.
14d.如图,ABCD,将一副直角三角板作如下摆放,∠GEF=60°,∠MNP=45°.下列结论:①GEMP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN.其中正确的是 .
15a.将长为20cm、宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x之间的关系式为 .
15b.如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为三角形ACE的面积为则与的关系式为 .
16.计算:
(1)
(2)
(3)
17.先化简,再求值
先化简,再求值:[(2x+y)(2x﹣y)﹣5x(x+2y)+(x+2y)2]÷(﹣3y),其中x=1,y=2.
先化简,再求值:,其中x,y满足.
18.已知,点是边上一点.
(1)利用尺规在的右侧以点为顶点作,使;(不写作法,保留作图痕迹)
(2)写出射线与的位置关系.
19.已知,是整数,解决以下问题:
(1)若,且,,求的值.
(2)若,且,求的值.
20.小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间与小红离家的距离的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是 米,小红在商店停留了 分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快的速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?
21.已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,则AD是 ∠BAC的平分线吗?若是说明理由.(在下面的括号内填注依据)
解:是,理由如下:
∵AD⊥BC,EG⊥BC ( 已知 ),
∴∠4=∠5=90 ( 垂直的定义),
∴AD ( );
∴∠1=∠E( ),
∠2= (两直线平行,内错角相等);
∵∠E=∠3(已知),
∴∠ =∠ (等量代换);
∴AD平分∠BAC( ).
22.用100米长的篱笆在地上围成一个矩形,当矩形的宽由小到大变化时,矩形的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)设矩形的宽为x(米),求矩形的面积y(平方米)与x的关系式;
(3)当矩形的宽由1米变化到25米时,矩形面积由(平方米)变化到(平方米),求和的值.
23.如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
24a.【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.
例如:如图1,,点、分别在直线、上,点在直线、之间.
(1)试说明:;
【类比应用】
(2)已知直线,P为平面内一点,连接、.
①如图2,已知,,求的度数,请说明理由.
②如图3,设、,猜想、、之间的数量关系为______.
24b.如图,已知AM∥BN,∠A=40°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数
24c.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2请你写出、、ab之间的等量关系是 ;
(2)根据(1)中的结论,若x+y=5,xy=,则x﹣y= ;
(3)拓展应用:若,求(2021﹣m)(m﹣2022)的值.
24d.数学活动课上,张老师准备了若干个如图的三种纸片,种纸片是边长为的正方形,种纸片是边长为的正方形,种纸片是长为宽为的长方形,并用种纸片一张,种纸片一张,种纸片两张拼成如图的大正方形.
观察图,请你写出代数式之间的等量关系是 ;
根据中的等量关系,解决下列问题;
已知,求的值;
已知,求的值.
1.下列运算正确的是( )
A. B. C. D.
2.今年肆虐全球的新冠肺炎(COVID﹣19)被世界卫生组织(WHO)标识为“全球大流行病”,它给全球人民带来了巨大的灾难.冠状病毒的直径约80﹣120nm,1nm为十亿分之一米,即10﹣9m.将120nm用科学记数法表示正确的是( )米.
A.1.2×10﹣7 B.1.2×10﹣8 C.120×10﹣9 D.12×10﹣8
3a.下列多项式乘法中可以用平方差公式计算的是( )
A. B. C. D.
3b.下列多项式乘法中不能用平方差公式计算的是( )
B. C. D.
4a.下列命题中,真命题的个数是( )
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;②两条直线被第三条直线所截,同旁内角互补;③两直线平行,内错角相等;④同一平面内,过一点有且只有一条直线与已知直线垂直;⑤从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
A.1个 B.2个 C.3个 D.4个
4b.下列四个命题中,正确的是( )
A.经过直线外一点,有且只有一条直线与这条直线平行
B.同旁内角相等,两直线平行
C.相等的角是对顶角
D.若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补
5a.下列图形中,线段PQ的长度表示点P到直线a的距离的是( )
5b.如图,,,垂足为D,,,,则点A到直线的距离为( )
A.5 B.4 C.3 D.
6a.如图,在四边形ABCD中,点E在BC上,连接DE,下列说法正确的是( )
A.因为∠A=∠B,所以AD∥BC B.因为∠B+∠DEB=180°,所以AB∥DE
C.因为∠B=∠DEC,所以AD∥BC D.因为∠B=∠EDC,所以AB∥DE
6b.如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2 B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2 D.在图4中,展开后测得∠1+∠2=180°
6c.如图,能判定AB∥CD的条件是( )
A.∠1=∠3 B.∠2=∠4
C.∠DCE=∠D D.∠B+∠BAD=180°
7a.在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg 0 1 2 3 4 5
y/cm 20 20.5 21 21.5 22 22.5
A.x与y都是变量,且x是自变量,y是x的函数
B.弹簧不挂重物时的长度为0 cm
C.物体质量每增加1 kg,弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时,弹簧长度为23.5 cm
7b. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
支撑物的高度 10 20 30 40 50 60 70
小车下滑的时间
下列说法正确的是( )
A. 当时, B. 随着h逐渐升高,t也逐渐变大
C. h每增加,t减小 D. 随着h逐渐升高,小车下滑的平均速度逐渐加快
7c.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量(升)与行驶时间(小时)之间的函数关系的图象是( )
A. B. C. D.
7d.如图,在长方形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则长方形ABCD的周长是( )
A.24 B.18 C.20 D.40
8a.如图将4个长、宽分别均为,的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
A. B.
C. D.
8b.边长分别为a和b(其中)的两个正方形按下图摆放,如果,,则图中阴影部分的面积为( )
A.25 B. C.13 D.
9a.已知,则 .
9b.已知:,,的值为 .
9c.已知a+2b-2=0,则3a×9b=_________.
10a若是一个完全平方式,则m的值为
10b.若多项式4a2-ka+16是一个完全平方式,则k=_________
10c若x2 +2mx + 16是关于x的完全平方式,则m= .
11a.若,,则 .
11b.若,那么的值为 .
12a.若(3x2﹣2x+1)(x﹣b)的积中不含x的一次项,则b的值为 .
12b.已知:化简的结果中不含项,则常数a的值是 .
13a.如果一个角的补角是150°,那么这个角的余角的度数是 .
13b.一个角的余角是它的,则这个角的补角等于 .
14a.如图,将一张长方形纸条沿折叠后,与交于点,若,则的度数为 .
14b.如图,∠BCD=90°,AB//DE,则与满足 .
14c.如图,,,,则 °.
14d.如图,ABCD,将一副直角三角板作如下摆放,∠GEF=60°,∠MNP=45°.下列结论:①GEMP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN.其中正确的是 .
15a.将长为20cm、宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x之间的关系式为 .
15b.如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为三角形ACE的面积为则与的关系式为 .
16.计算:
(1)
(2)
(3)
17.先化简,再求值
先化简,再求值:[(2x+y)(2x﹣y)﹣5x(x+2y)+(x+2y)2]÷(﹣3y),其中x=1,y=2.
先化简,再求值:,其中x,y满足.
18.已知,点是边上一点.
(1)利用尺规在的右侧以点为顶点作,使;(不写作法,保留作图痕迹)
(2)写出射线与的位置关系.
19.已知,是整数,解决以下问题:
(1)若,且,,求的值.
(2)若,且,求的值.
20.小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间与小红离家的距离的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是 米,小红在商店停留了 分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快的速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?
21.已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,则AD是 ∠BAC的平分线吗?若是说明理由.(在下面的括号内填注依据)
解:是,理由如下:
∵AD⊥BC,EG⊥BC ( 已知 ),
∴∠4=∠5=90 ( 垂直的定义),
∴AD ( );
∴∠1=∠E( ),
∠2= (两直线平行,内错角相等);
∵∠E=∠3(已知),
∴∠ =∠ (等量代换);
∴AD平分∠BAC( ).
22.用100米长的篱笆在地上围成一个矩形,当矩形的宽由小到大变化时,矩形的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)设矩形的宽为x(米),求矩形的面积y(平方米)与x的关系式;
(3)当矩形的宽由1米变化到25米时,矩形面积由(平方米)变化到(平方米),求和的值.
23.如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
24a.【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.
例如:如图1,,点、分别在直线、上,点在直线、之间.
(1)试说明:;
【类比应用】
(2)已知直线,P为平面内一点,连接、.
①如图2,已知,,求的度数,请说明理由.
②如图3,设、,猜想、、之间的数量关系为______.
24b.如图,已知AM∥BN,∠A=40°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数
24c.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2请你写出、、ab之间的等量关系是 ;
(2)根据(1)中的结论,若x+y=5,xy=,则x﹣y= ;
(3)拓展应用:若,求(2021﹣m)(m﹣2022)的值.
24d.数学活动课上,张老师准备了若干个如图的三种纸片,种纸片是边长为的正方形,种纸片是边长为的正方形,种纸片是长为宽为的长方形,并用种纸片一张,种纸片一张,种纸片两张拼成如图的大正方形.
观察图,请你写出代数式之间的等量关系是 ;
根据中的等量关系,解决下列问题;
已知,求的值;
已知,求的值.
同课章节目录
