云南省石林县鹿阜中学人教版八年级数学上册课件:13-1轴对称
文档属性
| 名称 | 云南省石林县鹿阜中学人教版八年级数学上册课件:13-1轴对称 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-23 08:48:54 | ||
图片预览








文档简介
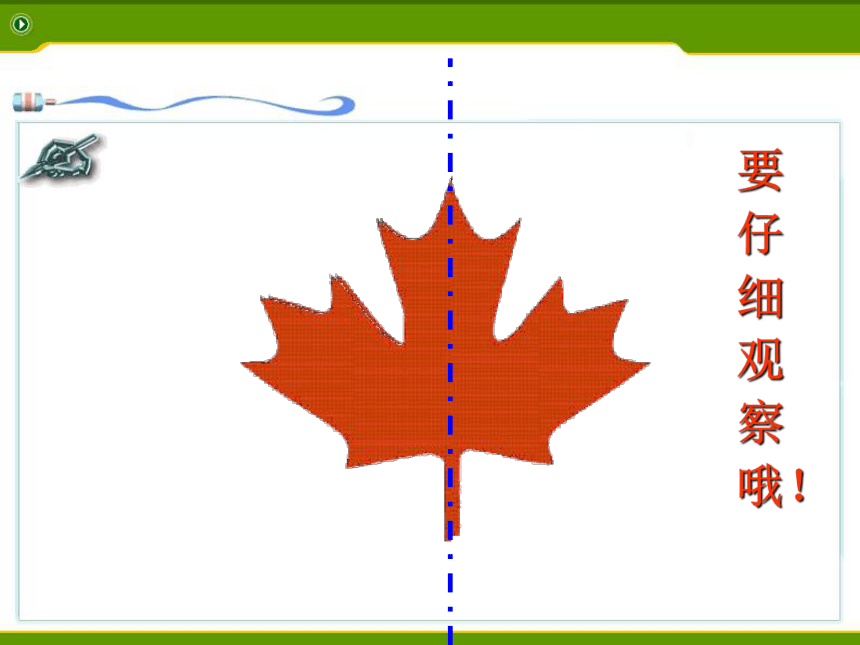
课件28张PPT。13.1 轴对称鹿阜中学 陈丽芬要仔细观察哦! 如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,这时,我们也说这个图形关于这条直线对称(或成轴对称) 。轴对称图形1.下列四个图形中,不是轴对称图形的是( )2.(2013·六盘水)下列图形中,是轴对称图形的是( )DA3.下列图案是轴对称图形的是( )D4.下列轴对称图形中,对称轴最多的是( )BA′ABCB′C′ 观察:下面的每对图形有什么共同特点? 把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。A′ABCB′C′两个图形成轴对称5.下列各组图形中,右边的图形与左边的图形成轴对称的有( ) A.1组 B.2组 C.3组 D.4组 B6.如图,这两个四边形关于某直线对称,根据图形的条件求x,y.解:x=70°
y=4C 你知道轴对称图形 和 两个图形成轴对称有什么区别和联系吗? 发现:可以把一个轴对称图形沿对称轴分成成轴对称的两个图形,也可以把成轴对称的两个图形看成是一个轴对称图形。想一想都是沿一条直线折叠后能够互相重合轴对称图形是一个图形。
两个图形成轴对称是两个图形之间的关系。 (1)有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。 (2)对称轴通常画成直线,不能画成线段。对称轴问题轴对称图形至少有一条对称轴。问题: 成轴对称的两个图形全等吗?全等的两个图形一定是轴对称吗?为什么?结论:成轴对称的两个图形一定全等,而全等的两个图形不一定是轴对称。追问1 你能说明其中的道理吗?
定义:经过线段的中点并且垂
直于这条线段,就叫这条线段
的垂直平分线,也叫中垂线。
探索新知 问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系?探索新知 追问2 上面的问题说明“如果△ABC 和
△A′B′C′关于直线MN 对称,那么,直线MN 垂直
线段AA′,BB′和CC′,并且直线MN 还平分线段
AA′,BB′和CC′”.如
果将其中的“三角形”改为
“四边形”“五边形”…其
他条件不变,上述结论还成
立吗? 探索新知 追问3 你能用数学语言概括前面的结论吗? 成轴对称的两个图形的性质:
如果两个图形关于某条
直线对称,那么对称轴是任
何一对对应点所连线段的垂
直平分线.即对称点所连线
段被对称轴垂直平分;对称
轴垂直平分对称点所连线段. 结论:
直线l 垂直线段AA′,BB′,
直线l平分线段AA′,BB′(或直
线l 是线段AA′,BB′的垂直平分
线). 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? 追问 你能用几何语言概括前面
的结论吗? 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? 轴对称图形的性质:
轴对称图形的对称轴,是任何
一对对应点所连线段的垂直平分线. 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? 7.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上,其中错误的有( )A.0个 B.1个
C.2个 D.3个A(1)本节课学习了哪些主要内容?
(2)轴对称图形和两个图形成轴对称的区别与联系是
什么?
(3)成轴对称的两个图形有什么性质?轴对称图形有
什么性质?我们是怎么探究这些性质的? 课堂小结谢谢
y=4C 你知道轴对称图形 和 两个图形成轴对称有什么区别和联系吗? 发现:可以把一个轴对称图形沿对称轴分成成轴对称的两个图形,也可以把成轴对称的两个图形看成是一个轴对称图形。想一想都是沿一条直线折叠后能够互相重合轴对称图形是一个图形。
两个图形成轴对称是两个图形之间的关系。 (1)有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。 (2)对称轴通常画成直线,不能画成线段。对称轴问题轴对称图形至少有一条对称轴。问题: 成轴对称的两个图形全等吗?全等的两个图形一定是轴对称吗?为什么?结论:成轴对称的两个图形一定全等,而全等的两个图形不一定是轴对称。追问1 你能说明其中的道理吗?
定义:经过线段的中点并且垂
直于这条线段,就叫这条线段
的垂直平分线,也叫中垂线。
探索新知 问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系?探索新知 追问2 上面的问题说明“如果△ABC 和
△A′B′C′关于直线MN 对称,那么,直线MN 垂直
线段AA′,BB′和CC′,并且直线MN 还平分线段
AA′,BB′和CC′”.如
果将其中的“三角形”改为
“四边形”“五边形”…其
他条件不变,上述结论还成
立吗? 探索新知 追问3 你能用数学语言概括前面的结论吗? 成轴对称的两个图形的性质:
如果两个图形关于某条
直线对称,那么对称轴是任
何一对对应点所连线段的垂
直平分线.即对称点所连线
段被对称轴垂直平分;对称
轴垂直平分对称点所连线段. 结论:
直线l 垂直线段AA′,BB′,
直线l平分线段AA′,BB′(或直
线l 是线段AA′,BB′的垂直平分
线). 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? 追问 你能用几何语言概括前面
的结论吗? 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? 轴对称图形的性质:
轴对称图形的对称轴,是任何
一对对应点所连线段的垂直平分线. 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? 7.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上,其中错误的有( )A.0个 B.1个
C.2个 D.3个A(1)本节课学习了哪些主要内容?
(2)轴对称图形和两个图形成轴对称的区别与联系是
什么?
(3)成轴对称的两个图形有什么性质?轴对称图形有
什么性质?我们是怎么探究这些性质的? 课堂小结谢谢
