云南省石林县鹿阜中学人教版九年级数学上册课件:23-1图形的旋转
文档属性
| 名称 | 云南省石林县鹿阜中学人教版九年级数学上册课件:23-1图形的旋转 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-23 00:00:00 | ||
图片预览


文档简介
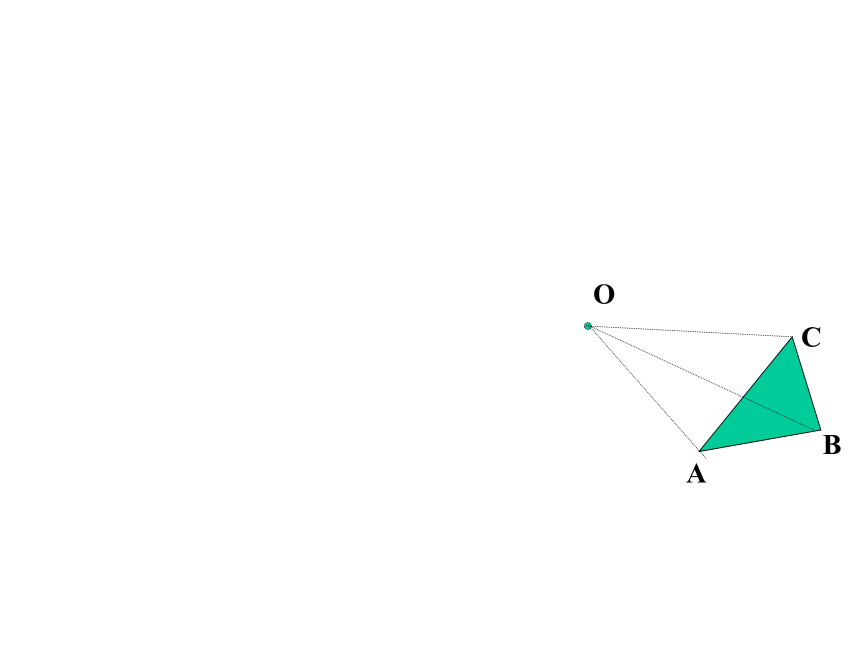
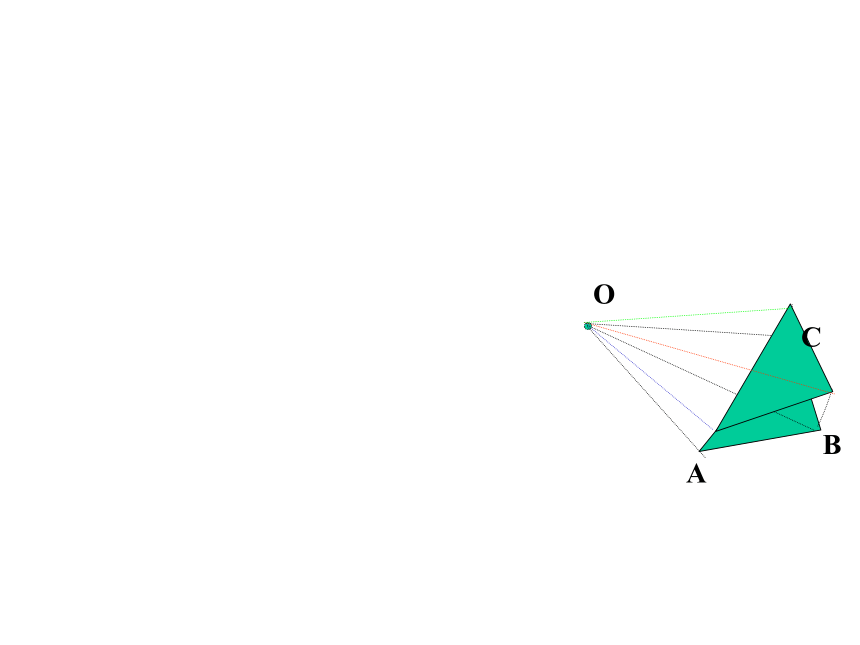
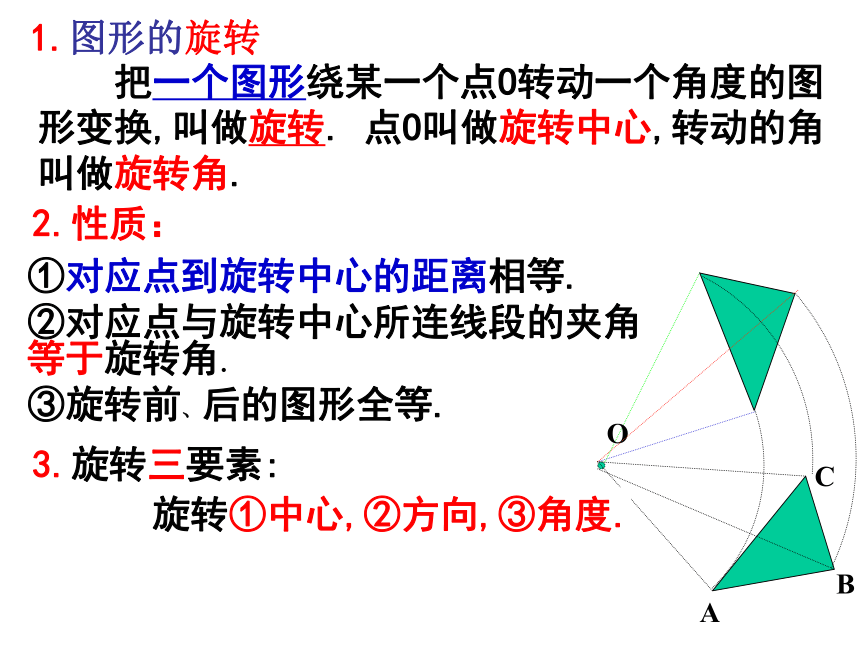
课件56张PPT。图形的旋转八年级----张兵 ABCOABCOABCO旋转①中心,②方向,③角度.3.旋转三要素:1.图形的旋转2.性质: 把一个图形绕某一个点O转动一个角度的图形变换,叫做旋转. 点O叫做旋转中心,转动的角叫做旋转角.①对应点到旋转中心的距离相等.
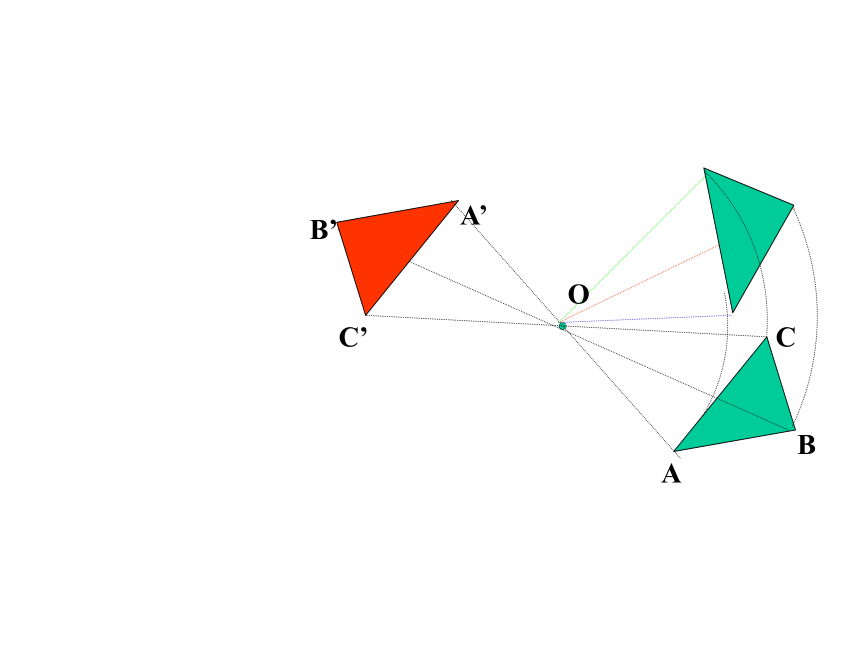
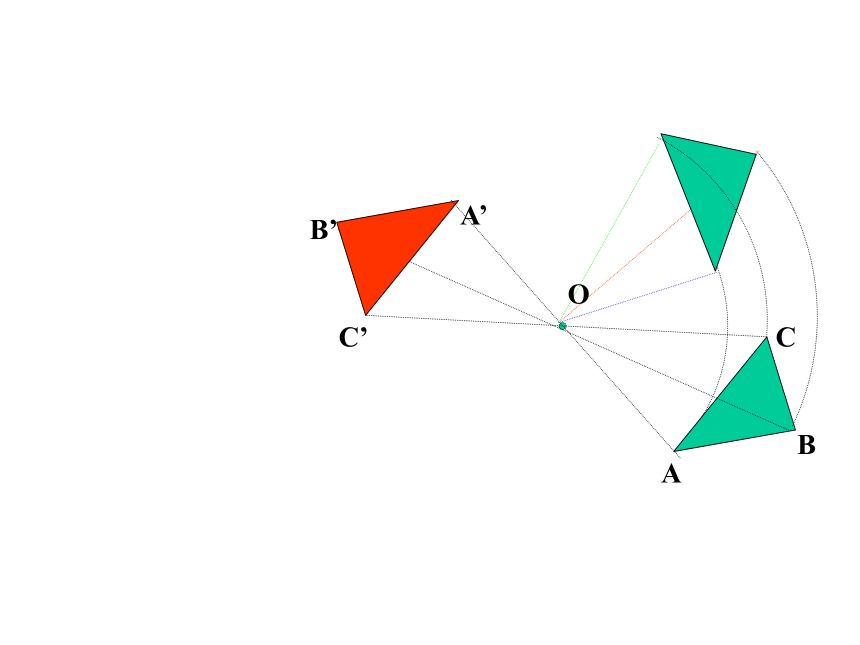
②对应点与旋转中心所连线段的夹角等于旋转角.
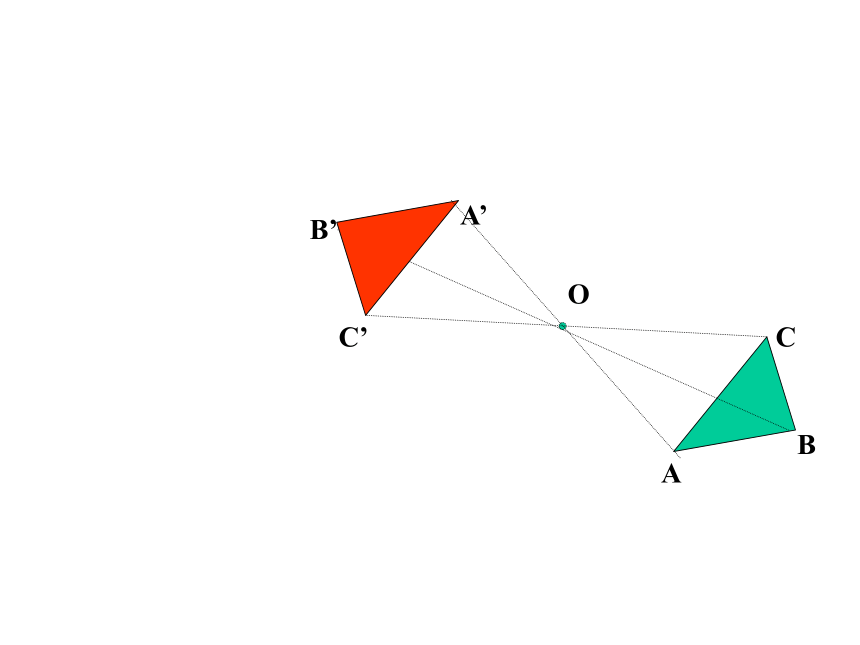
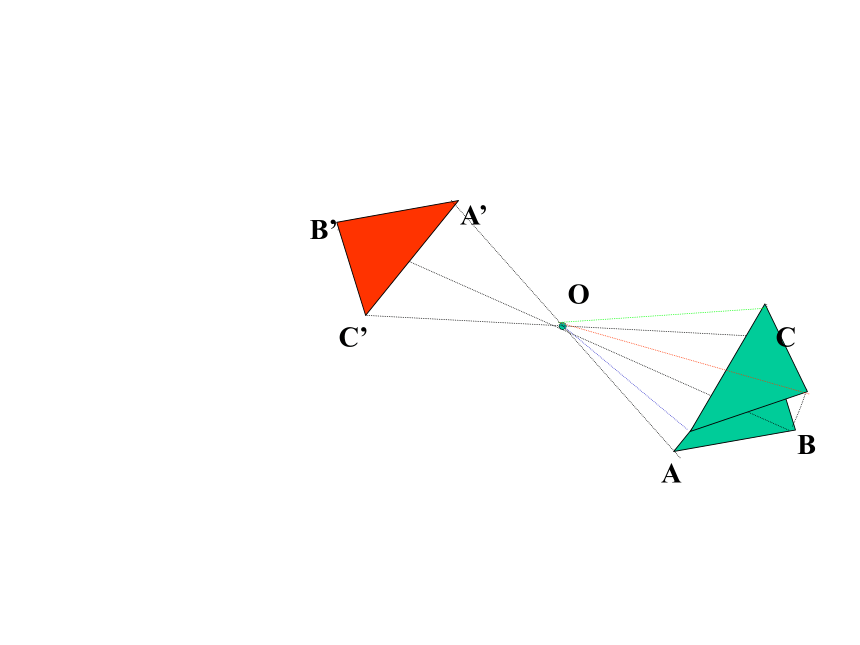
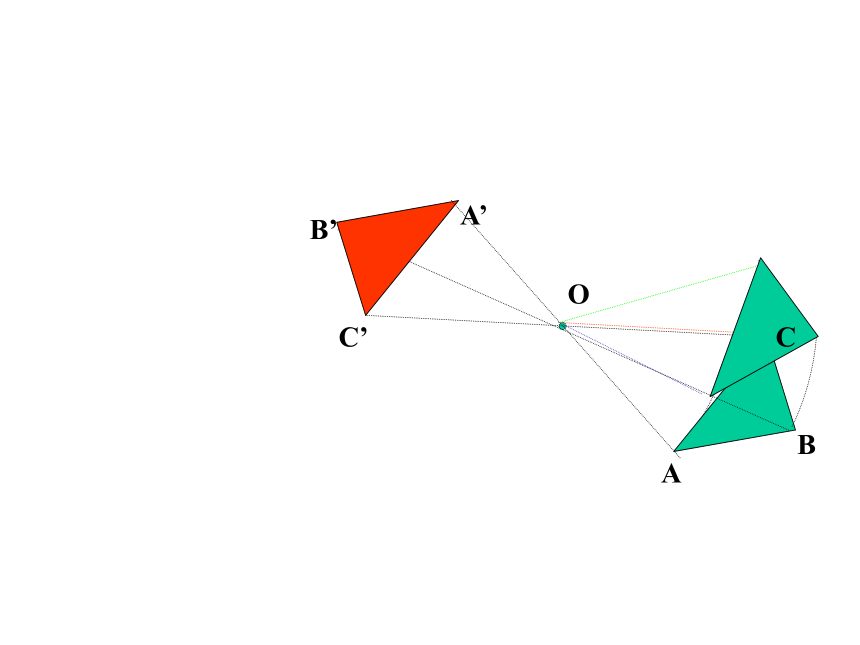
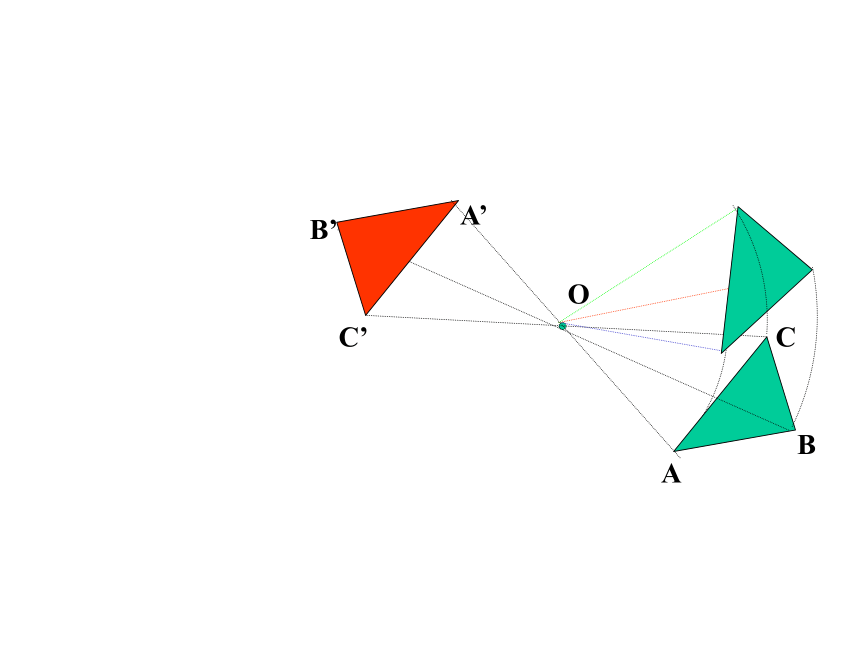
③旋转前、后的图形全等.ABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’O中心对称:把一个图形绕着某一个点旋转180°,如果它
能与另一个图形重合,那么就说这两个图形关
于这个点对称或中心对称ABCA’C’B’O 性质:①两个图形全等.
②对称中心平分两个对应点所连的线段.中心对称图形:
如果一个图形绕一个点旋转1800后,与原来的图形能够互相重合,那么这个图形叫做中心对称图形,这个点叫做对称中心.中心对称与中心对称图形的联系与区别。旋转的概念及识别 绕一定点旋转180?后与原来图形重合的图形是中心对称图形,正六边形就是这样的图形,小明发现将正六边形绕着它的中心旋转一个小于180?的角,也可以使它与原来的正六边形重合.请你写出小明发现的一个旋转角的度数__________60?或120? 请观察并指出下列四个图形中,哪些是中心对称图形,哪些是旋转图形,讲出你的依据.(1) (2) (3) (4) 请从最小旋转角的大小给下列旋转图形分类 A B C D E F G H最小旋转角是90°的有:A,D,H最小旋转角是180 °的有:B,E,G最小旋转角是120 °的有:C最小旋转角是60°的有:F中心对称的概念理解不准确在0到9的十个数字中,成中心对称的数字有
哪些?试写出来中心对称图形的定义掌握不牢下面图形中是中心对称图形的有:①线段②角
③等边三角形④矩形⑤平行四边形中心对称常见病错解:0,1,8正解:6和9利用对称探求规律(2004年烟台) 把26个英文字母按规律分成5组,现在还有5个字母D、M 、 Q 、 X 、 Z,请按原规律补上,其顺序依次为( )
①FRPJ LG______ ②HIO______③NS______
④BCKE________ ⑤VATYWU________
A.QXZMD B.DMQZX
C.ZXMDQ D.QXZDMD中心对称在实际生活中的应用 小强在一节数学课上,在平面直角坐标系中,将坐标为(1,0), (6,4), (4,0), (6,1), (6,-1), (4,0), (5,-2), (1,0)的点,用线段依次连接成一条鱼,如图所示,接着他想再画一条鱼,使这两条鱼关于原点对称, 他能做到吗? 图中,正比例函数和反比例函数的图象相交于A,B两点,分别以A,B两点为圆心画圆,圆的半径都为1,则圆中两个阴影面积的和是_________oxyAB∏感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.CEFGABD变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.CEFGBAD变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.CEFGBAD变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.ABCDEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.图2ABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.D变式训练二:若将正方形ABCD绕点C按顺时针方向继续旋转至如图3的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.ABCEFGD图3数学与对称美图片欣赏请你谈谈本节课的收获
……金榜题名!祝同学们:
②对应点与旋转中心所连线段的夹角等于旋转角.
③旋转前、后的图形全等.ABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’OABCA’C’B’O中心对称:把一个图形绕着某一个点旋转180°,如果它
能与另一个图形重合,那么就说这两个图形关
于这个点对称或中心对称ABCA’C’B’O 性质:①两个图形全等.
②对称中心平分两个对应点所连的线段.中心对称图形:
如果一个图形绕一个点旋转1800后,与原来的图形能够互相重合,那么这个图形叫做中心对称图形,这个点叫做对称中心.中心对称与中心对称图形的联系与区别。旋转的概念及识别 绕一定点旋转180?后与原来图形重合的图形是中心对称图形,正六边形就是这样的图形,小明发现将正六边形绕着它的中心旋转一个小于180?的角,也可以使它与原来的正六边形重合.请你写出小明发现的一个旋转角的度数__________60?或120? 请观察并指出下列四个图形中,哪些是中心对称图形,哪些是旋转图形,讲出你的依据.(1) (2) (3) (4) 请从最小旋转角的大小给下列旋转图形分类 A B C D E F G H最小旋转角是90°的有:A,D,H最小旋转角是180 °的有:B,E,G最小旋转角是120 °的有:C最小旋转角是60°的有:F中心对称的概念理解不准确在0到9的十个数字中,成中心对称的数字有
哪些?试写出来中心对称图形的定义掌握不牢下面图形中是中心对称图形的有:①线段②角
③等边三角形④矩形⑤平行四边形中心对称常见病错解:0,1,8正解:6和9利用对称探求规律(2004年烟台) 把26个英文字母按规律分成5组,现在还有5个字母D、M 、 Q 、 X 、 Z,请按原规律补上,其顺序依次为( )
①FRPJ LG______ ②HIO______③NS______
④BCKE________ ⑤VATYWU________
A.QXZMD B.DMQZX
C.ZXMDQ D.QXZDMD中心对称在实际生活中的应用 小强在一节数学课上,在平面直角坐标系中,将坐标为(1,0), (6,4), (4,0), (6,1), (6,-1), (4,0), (5,-2), (1,0)的点,用线段依次连接成一条鱼,如图所示,接着他想再画一条鱼,使这两条鱼关于原点对称, 他能做到吗? 图中,正比例函数和反比例函数的图象相交于A,B两点,分别以A,B两点为圆心画圆,圆的半径都为1,则圆中两个阴影面积的和是_________oxyAB∏感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.感悟旋转的魅力如图,正方形ABCD的边CD在正方形ECGF的边CE上连接BE,DG.图中是否存在通过旋转能够互相重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.CEFGABD变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.CEFGBAD变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.CEFGBAD变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.ABCDEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.图2ABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.DABCEFG变式训练一:若将正方形ABCD绕点C按顺时针方向旋转至如图2的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.D变式训练二:若将正方形ABCD绕点C按顺时针方向继续旋转至如图3的位置,图中是否还存在通过旋转能够重合的两个三角形,若存在,请说出旋转过程,若不存在,请说明理由.ABCEFGD图3数学与对称美图片欣赏请你谈谈本节课的收获
……金榜题名!祝同学们:
同课章节目录
