苏科版八年级上册3.2勾股定理的逆定理 课件 (共30张PPT)
文档属性
| 名称 | 苏科版八年级上册3.2勾股定理的逆定理 课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 18:26:44 | ||
图片预览








文档简介
(共30张PPT)
勾股逆定理
知识梳理
课堂练习
目 录
勾 股 逆 定 理
a
b
c
如果三角形的三条边长a、b、c,满足a +b =c ,那么这个三角形是直角三角形。
A
B
C
判定直角三角形的一般步骤:
(1)首先确定最大边
(2)验证c 与a +b 是否具有相等关系,若c =a +b ,则△ABC是
∠C=90°的直角三角形;若c ≠a +b ,则△ABC不是直角三角形。
知 识 梳 理
b
C
a
知 识 梳 理
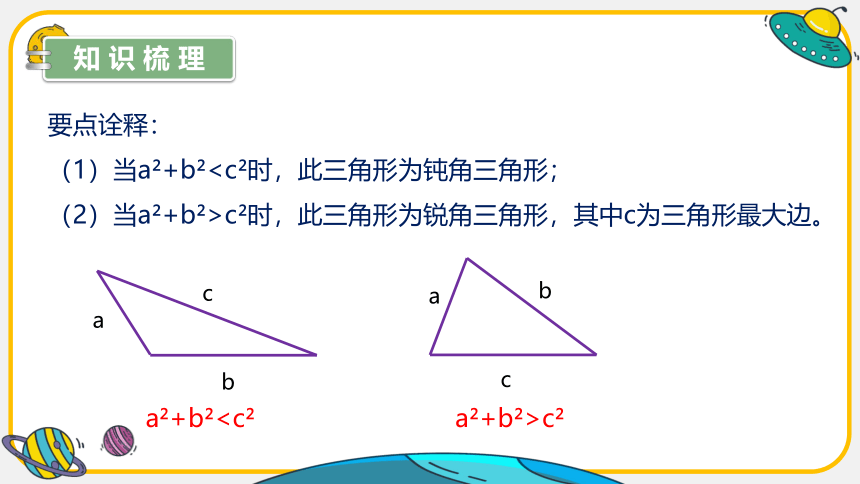
要点诠释:
(1)当a +b(2)当a +b >c 时,此三角形为锐角三角形,其中c为三角形最大边。
a
b
c
a +b >c
a
b
c
a +b类型一、勾股定理的逆定理
例1. 发现下列几组数据能作为三角形的边:
(1)8,15,17;(2)5,12,13;(3)12,15,20;(4)7,24,25.
其中能作为直角三角形的三边长的有( )
A. 1组 B. 2组 C. 3组 D. 4组
举一反三:
2.若△ABC的两边长为8和15,则能使△ ABC为直角三角形的第三边的平
方是( )
A.161; B.289; C.17; D.161或289.
类型二、勾股定理逆定理的应用
例2. 已知:a、b、c为△ABC的三边且满足a +b +c +338=10a+24b+26c,试判断△ABC的形状
举一反三:
【变式】已知a、b、c为△ABC三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状
类型三、勾股定理逆定理的实际应用
例3. 已知某校有一块四边形空地ABCD,如图,现计划在该空地上种草皮,经测量
∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m, 若每平方米草皮需
100元,问需投入多少元?
举一反三:
【变式】如图,铁路MN和铁路PQ在P点处交汇,点A处是第九十四中学,AP=160米,点A到铁路MN的距离为80米,假使火车行驶时,周围100米以内会受到噪音影响.
(1)火车在铁路MN上沿PN方向行驶时,学校是否会受到影响?请说明理由.
(2)如果受到影响,已知火车的速度是180千米/时那么学校受到影响的时间是多久?
课堂练习
02
1. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b=8,c=10 D.a=3,b=4,c=5
2. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成
一个直角三角形三边的线段是( ).
A.CD、EF、GH B.AB、EF、GH C.AB、CF、EF D.GH、AB、CD
3. 下列说法:
(1)在△ABC中,若a2+b2≠c2,则△ABC不是直角三角形;
(2)若△ABC是直角三角形,∠C=90°,则a2+b2=c2;
(3)在△ABC中,若a2+b2=c2,则∠C=90°;
(4)直角三角形的两条直角边的长分别为5和12,则斜边上的高为.
其中说法正确的有( ).
A.4个 B.3个 C.2个 D.1个
4. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
5. 已知三角形的三边长为 n、n+1、m(其中m =2n+1),则此三角形( ).
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
6. 三角形的三边长分别为a +b 、2ab、a -b (a、b都是正整数),则这个三角形是( ).
A.直角三角形 B. 钝角三角形 C.锐角三角形 D.不能确定
7.(2015 本溪模拟)如图,在2×2的正方形网格中有9个格点,已经取定点A和B,
在余下的7个点中任取一点C,使△ABC为直角三角形的点C有 个.
8. 若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 .
9. △ABC的3条边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1.证明△ABC是直角三角形。
10. 已知:如图,在正方形ABCD中,F为DC的中点,E为CB的四等分点且CE=CB,
求证:AF⊥FE.
11. 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,
∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?
12. 如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开
始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速
度移动,如果同时出发,则过3秒时,△BPQ的面积为多少平方厘米?
13. 已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,判断△ABC的形状。
14. 一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
15. 如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,
BC=10cm,求EC的长.
16. 如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱
17. 一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
下次课见
勾股逆定理
知识梳理
课堂练习
目 录
勾 股 逆 定 理
a
b
c
如果三角形的三条边长a、b、c,满足a +b =c ,那么这个三角形是直角三角形。
A
B
C
判定直角三角形的一般步骤:
(1)首先确定最大边
(2)验证c 与a +b 是否具有相等关系,若c =a +b ,则△ABC是
∠C=90°的直角三角形;若c ≠a +b ,则△ABC不是直角三角形。
知 识 梳 理
b
C
a
知 识 梳 理
要点诠释:
(1)当a +b
a
b
c
a +b >c
a
b
c
a +b
例1. 发现下列几组数据能作为三角形的边:
(1)8,15,17;(2)5,12,13;(3)12,15,20;(4)7,24,25.
其中能作为直角三角形的三边长的有( )
A. 1组 B. 2组 C. 3组 D. 4组
举一反三:
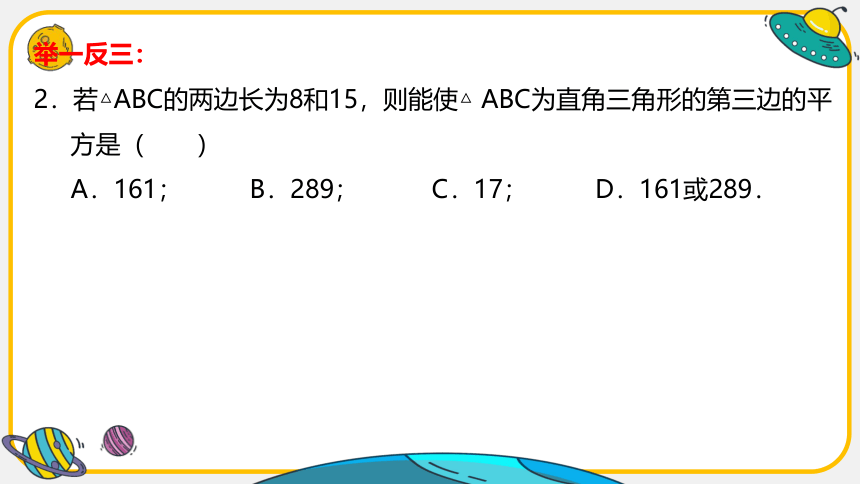
2.若△ABC的两边长为8和15,则能使△ ABC为直角三角形的第三边的平
方是( )
A.161; B.289; C.17; D.161或289.
类型二、勾股定理逆定理的应用
例2. 已知:a、b、c为△ABC的三边且满足a +b +c +338=10a+24b+26c,试判断△ABC的形状
举一反三:
【变式】已知a、b、c为△ABC三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状
类型三、勾股定理逆定理的实际应用
例3. 已知某校有一块四边形空地ABCD,如图,现计划在该空地上种草皮,经测量
∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m, 若每平方米草皮需
100元,问需投入多少元?
举一反三:
【变式】如图,铁路MN和铁路PQ在P点处交汇,点A处是第九十四中学,AP=160米,点A到铁路MN的距离为80米,假使火车行驶时,周围100米以内会受到噪音影响.
(1)火车在铁路MN上沿PN方向行驶时,学校是否会受到影响?请说明理由.
(2)如果受到影响,已知火车的速度是180千米/时那么学校受到影响的时间是多久?
课堂练习
02
1. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b=8,c=10 D.a=3,b=4,c=5
2. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成
一个直角三角形三边的线段是( ).
A.CD、EF、GH B.AB、EF、GH C.AB、CF、EF D.GH、AB、CD
3. 下列说法:
(1)在△ABC中,若a2+b2≠c2,则△ABC不是直角三角形;
(2)若△ABC是直角三角形,∠C=90°,则a2+b2=c2;
(3)在△ABC中,若a2+b2=c2,则∠C=90°;
(4)直角三角形的两条直角边的长分别为5和12,则斜边上的高为.
其中说法正确的有( ).
A.4个 B.3个 C.2个 D.1个
4. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
5. 已知三角形的三边长为 n、n+1、m(其中m =2n+1),则此三角形( ).
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
6. 三角形的三边长分别为a +b 、2ab、a -b (a、b都是正整数),则这个三角形是( ).
A.直角三角形 B. 钝角三角形 C.锐角三角形 D.不能确定
7.(2015 本溪模拟)如图,在2×2的正方形网格中有9个格点,已经取定点A和B,
在余下的7个点中任取一点C,使△ABC为直角三角形的点C有 个.
8. 若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 .
9. △ABC的3条边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1.证明△ABC是直角三角形。
10. 已知:如图,在正方形ABCD中,F为DC的中点,E为CB的四等分点且CE=CB,
求证:AF⊥FE.
11. 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,
∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?
12. 如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开
始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速
度移动,如果同时出发,则过3秒时,△BPQ的面积为多少平方厘米?
13. 已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,判断△ABC的形状。
14. 一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
15. 如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,
BC=10cm,求EC的长.
16. 如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱
17. 一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
下次课见
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
