北师大版数学九年级上册第二章 一元二次方程 综合素质评价(含答案)
文档属性
| 名称 | 北师大版数学九年级上册第二章 一元二次方程 综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 241.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 19:01:49 | ||
图片预览



文档简介
第二章综合素质评价
一、选择题(共10小题,每小题3分,共30分)
1.下列方程中,关于x的一元二次方程是( )
A.2(x2+2x)=2x2-1 B.ax2+bx+c=0
C.(x+1)2=2x+1 D.+x+1=0
2.如果关于x的方程(x-9)2=m+4可以用直接开平方法求解,那么m的取值范围是( )
A.m>3 B.m≥3 C.m>-4 D.m≥-4
3.将一元二次方程2x2-6x+1=0配方,得(x+h)2=k,则h,k的值分别为( )
A.3、8 B.-3、8 C.、 D.-、
4.[2024北京海淀区月考]在下列方程中,有一个方程有两个实数根,且它们互为相反数,这个方程是( )
A.x-1=0 B.x2+x=0 C.x2-1=0 D.x2+1=0
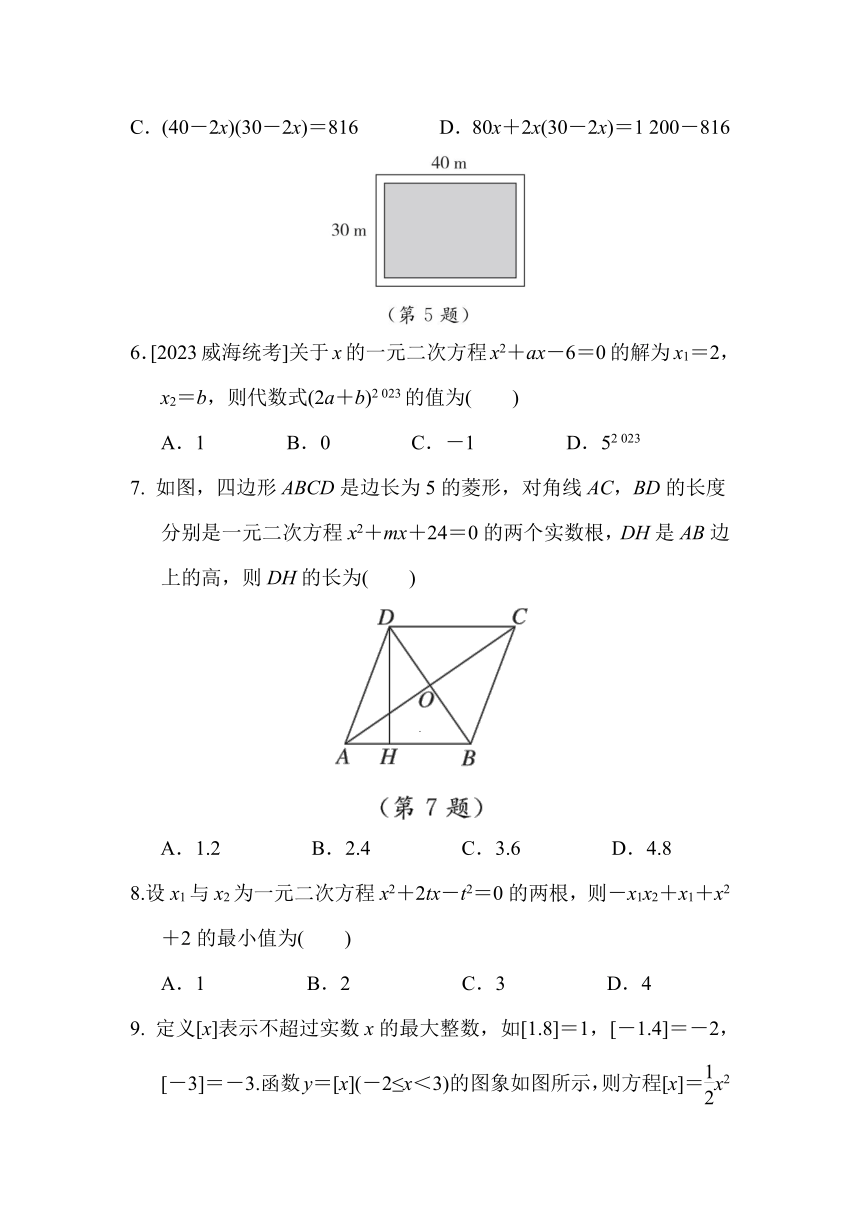
5. 加快推动生态建设步伐,形成“城在林中、园在城中、山水相依、林路相随”的生态格局,市政府计划在某街心公园的一块矩形空地上修建草坪.如图,矩形长为40 m,宽为30 m,在矩形内的四周修筑同样宽的道路,余下的部分(图中阴影部分)铺上草坪.要使草坪的面积为816 m2,道路的宽度应为多少?设矩形地块四周道路的宽度为x m,根据题意,下列方程不正确的是( )
A.1 200-(80x+60x-4x2)=816 B.(40-x)(30-x)=816
C.(40-2x)(30-2x)=816 D.80x+2x(30-2x)=1 200-816
6.[2023威海统考]关于x的一元二次方程x2+ax-6=0的解为x1=2,x2=b,则代数式(2a+b)2 023的值为( )
A.1 B.0 C.-1 D.52 023
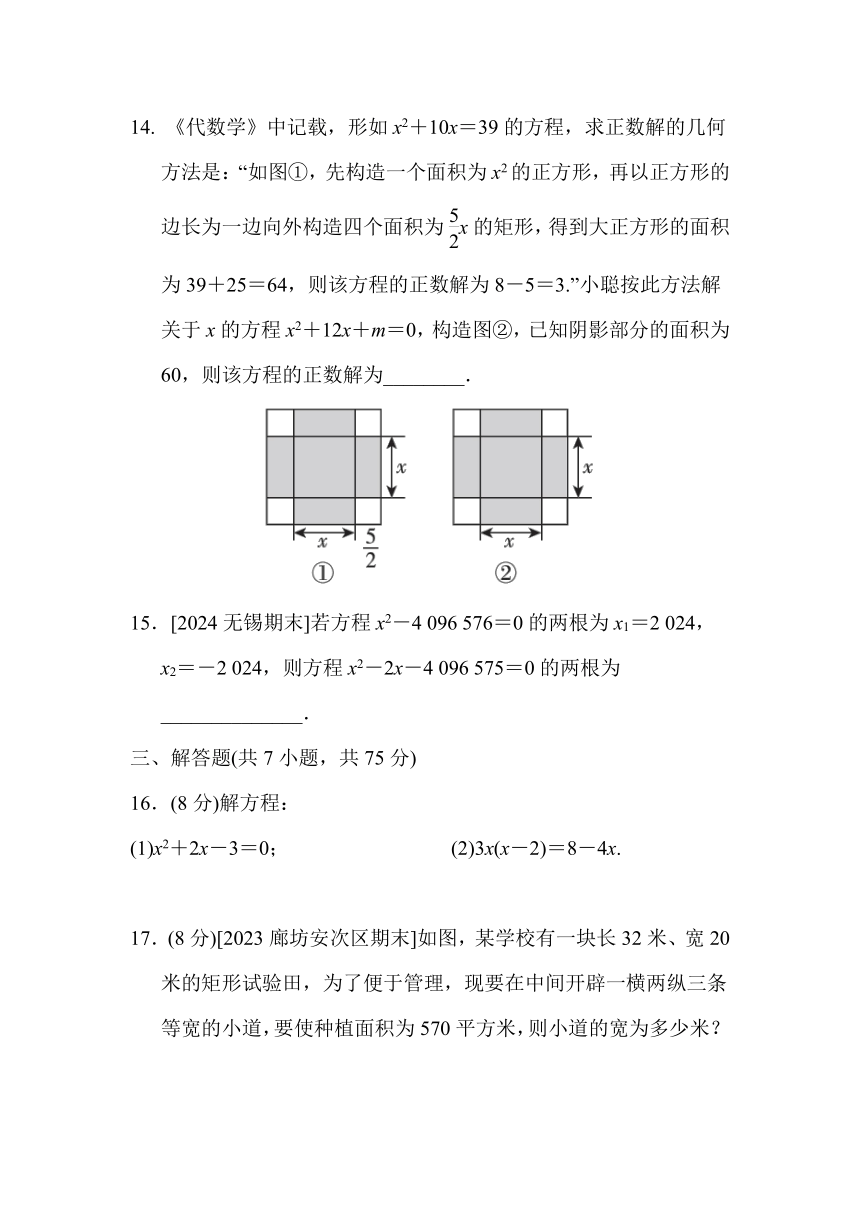
7. 如图,四边形ABCD是边长为5的菱形,对角线AC,BD的长度分别是一元二次方程x2+mx+24=0的两个实数根,DH是AB边上的高,则DH的长为( )
A.1.2 B.2.4 C.3.6 D.4.8
8.设x1与x2为一元二次方程x2+2tx-t2=0的两根,则-x1x2+x1+x2+2的最小值为( )
A.1 B.2 C.3 D.4
9. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x](-2≤x<3)的图象如图所示,则方程[x]=x2的解为x=( )
A.0或或2 B.0或 C.1或- D.或-
10.一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中ac≠0,a≠c,给出以下四个结论:①若方程M有两个不相等的实数根,则方程N也有两个不相等的实数根;②若方程M的两根符号相同,则方程N的两根符号也相同;③若m是方程M的一个根,则是方程N的一个根;④若方程M和方程N有一个相同的根,则这个根必是x=1,其中正确的结论是( )
A.①③ B.①②③ C.①②④ D.①③④
二、填空题(共5小题,每小题3分,共15分)
11. 若关于x的一元二次方程(k-1)x2+6x+k2-k=0的一个根是0,则k的值是________.
12.若关于x的一元二次方程x2-6x+k=0有两个不相等的实数根,则k的取值范围是________.
13.一个两位数,其个位上的数与十位上的数的和等于6,而个位与十位上的数的积等于这两位数的三分之一,则这个两位数为________.
14. 《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3.”小聪按此方法解关于x的方程x2+12x+m=0,构造图②,已知阴影部分的面积为60,则该方程的正数解为________.
15.[2024无锡期末]若方程x2-4 096 576=0的两根为x1=2 024, x2=-2 024,则方程x2-2x-4 096 575=0的两根为______________.
三、解答题(共7小题,共75分)
16.(8分)解方程:
(1)x2+2x-3=0; (2)3x(x-2)=8-4x.
17.(8分)[2023廊坊安次区期末]如图,某学校有一块长32米、宽20米的矩形试验田,为了便于管理,现要在中间开辟一横两纵三条等宽的小道,要使种植面积为570平方米,则小道的宽为多少米?
18.(10分)在欧几里得的《几何原本》中,形如x2+ax=b2的一元 二次方程通过图解法能得到其中的一个正根:如图,先画Rt△ACB,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=,连接CD,那么图中某条线段的长就是一元二次方程的其中一个正根.
(1)用含a,b的代数式表示AD的长.
(2)图中哪条线段的长是一元二次方程x2+ax=b2的一个正根?请说明理由.
19.(10分)关于x的一元二次方程a(1-x2)-2bx+c(1+x2)=0中,a,b,c是Rt△ABC的三条边,其中∠C=90°.
(1)求证:此方程有两个不相等的实数根;
(2)若方程的两个根是x1,x2,且x12+x22=12,求a:b:c.
20.(12分) 阅读下列材料,并用相关的思想方法解决问题.材料:为解方程x4-x2-6=0,可将方程变形为(x2)2-x2-6=0,然后设x2=y,则(x2)2=y2,原方程化为y2-y-6=0…①
解得y1=-2,y2=3,当y1=-2时,x2=-2无意义,舍去;
当y2=3时,x2=3,解得x=±;
所以原方程的解为x1=,x2=-.
问题:(1)在原方程得到方程①的过程中,利用________法达到了降次的目的,体现了________的数学思想;
(2)利用以上学习到的方法解方程(x2+5x+1)(x2+5x+7)=7.
21.(12分)某种商品的标价为200元/件,经过两次降价后的价格为162元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为156元/件,以200元/件的价格售出,平均每天能售出20件,另外每天需支付其他各种费用150元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出 5件,如果每天盈利1 450元,每件应降价多少元?
22.(15分) 如图所示,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.
(1)点P从点A开始沿AB边向B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒,△PBQ的面积等于8 cm2
(2)在(1)的基础上,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点P沿射线AB方向从点A出发以1 cm/s的速度移动,同时点Q沿射线CB方向从C点出发以2 cm/s的速度移动,经过几秒,△PBQ的面积为1 cm2
INCLUDEPICTURE"章3.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章3.EPS" \* MERGEFORMATINET 答案
一、1.C 2.D 3.D 4.C 5.B
6.C 【点拨】将x1=2代入x2+ax-6=0,得22+2a-6=0,
解得a=1,
∴关于x的一元二次方程为x2+x-6=0,
解得x1=2,x2=-3,即b=-3.
将a=1,b=-3代入(2a+b)2 023,
得(2a+b)2 023=[2×1+(-3)]2 023=(-1)2 023=-1,
故选C.
7.B 【点拨】∵四边形ABCD是边长为5的菱形,DH是AB边上的高,
∴S菱形ABCD=AC·BD=AB·DH,AB=5.
∴AC·BD=5DH.
∵对角线AC,BD的长度分别是一元二次方程x2+mx+24=0的两实数根,
∴AC·BD=x1·x2==24.
∴×24=5DH.
∴DH==2.4.
故选B.
8.A 【点拨】根据题意,得x1x2=-t2,x1+x2=-2t,
则-x1x2+x1+x2+2=t2-2t+2=(t-1)2+1.
∵(t-1)2≥0,
∴(t-1)2+1≥1.
∴-x1x2+x1+x2+2的最小值为1.
故选A.
9.A 【点拨】当2≤x<3时,x2=2,
解得x1=2,x2=-2(舍去);
当1≤x<2时,x2=1,
解得x1=,x2=-(舍去);
当0≤x<1时,x2=0,解得x=0;
当-1≤x<0时,x2=-1,方程没有实数解;
当-2≤x<-1时,x2=-2,方程没有实数解,
∴方程[x]=x2的解为x=0或x=或x=2.
故选A.
10.B 【点拨】∵M:ax2+bx+c=0有两个不相等的实数根,
∴Δ=b2-4ac>0.
∵N:cx2+bx+a=0的判别式为Δ=b2-4ca=b2-4ac>0,
∴方程N也有两个不相等的实数根,故①正确;
∵M:ax2+bx+c=0的两根符号相同,
∴Δ=b2-4ac≥0,>0.
∴Δ=b2-4ac≥0, >0.
∴方程N的两根符号也相同,故②正确;
∵m是方程M:ax2+bx+c=0的一个根,
∴am2+bm+c=0.
∵+b×+a==0,
∴是方程N的一个根,故③正确;
设方程M和方程N相同的根为x0,
根据题意,得ax02+bx0+c=0,cx02+bx0+a=0,
∴(a-c)x02=a-c.
∵ac≠0,a≠c,
∴x02=1,解得x0=±1,
故这个根是x=±1,故④错误;
故选B.
二、11.0 12.k<9
13.24或15 【点拨】设个位上的数为x,
则十位上的数为(6-x),
由题意得,x(6-x)=[10(6-x)+x],
解得x1=4,x2=5.
∴十位上的数为6-4=2或6-5=1.
∴这个两位数是24或15.
14.4-6 【点拨】x2+12x+m=0,
x2+12x=-m.
∵阴影部分的面积为60,
∴x2+12x=60.
设矩形的宽为a,∴4a=12,则a=3.
同理:先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为3x的矩形,得到大正方形的面积为60+32×4=60+36=96,则该方程的正数解为-6=4-6.
15.x1=2 025,x2=-2 023 【点拨】x2-2x-4 096 575=0,
则x2-2x=4 096 575,
∴x2-2x+1=4 096 575+1.
∴(x-1)2=4 096 576.
∴x-1=±2 024.
∴x1=2 025,x2=-2 023.
三、16.【解】(1)原方程变为(x+3)(x-1)=0,
∴x+3=0或x-1=0.
∴x1=-3,x2=1.
(2)原方程变为3x(x-2)+4(x-2)=0,
∴(x-2)(3x+4)=0.
∴x-2=0或3x+4=0.
∴x1=2,x2=-.
17.【解】设小道的宽为x米,则剩余部分可合成长为(32-2x)米,宽为(20-x)米的矩形,
根据题意得(32-2x)(20-x)=570,
整理得x2-36x+35=0,
解得x1=1,x2=35(不符合题意,舍去).
∴小道的宽为1米.
18.【解】(1)∵∠ACB=90°,BC=,AC=b,
∴AB===.
∴AD=AB-BD=-=.
(2)线段AD的长是一元二次方程x2+ax=b2的一个正根.理由如下:
设AD=m,则AB=AD+BD=m+.
在Rt△ABC中,由勾股定理得b2+=,
整理,得m2+am=b2,
∴线段AD的长是一元二次方程x2+ax=b2的一个正根.
19.(1)【证明】关于x的一元二次方程a(1-x2)-2bx+c(1+x2)=0去括号,整理为一般形式为(c-a)x2-2bx+a+c=0,
∴Δ=(-2b)2-4(a+c)(c-a)=4(2b2+a2-c2).
∵a,b,c是Rt△ABC的三条边,其中∠C=90°,
∴b2+a2-c2=0.
∴2b2+a2-c2>0.
∴Δ=4(2b2+a2-c2)>0.
∴此方程有两个不相等的实数根.
(2)【解】∵方程的两个根是x1,x2,
∴x1+x2=-,x1x2=.
∵x12+x22=12,
∴(x1+x2)2-2x1x2=12,即-=12.
∵b2=c2-a2,∴-=12.
∴-=12.
∴=12.
∴c+a=2c-2a.
∴3a=c.
∴b2=8a2.
∴b=2a.
∴a:b:c=1:2:3.
20.【解】(1)换元;化归
(2)令y=x2+5x,
则原方程化为(y+1)(y+7)=7,
整理,得y2+8y=0,
解得y1=0,y2=-8.
当y=0时,x2+5x=0,
解得x1=0,x2=-5;
当y=-8时,x2+5x=-8,即x2+5x+8=0.
∵Δ=52-4×1×8=-7<0,
∴此方程无实数解.
综上,方程(x2+5x+1)(x2+5x+7)=7的解
为x1=0,x2=-5.
21.【解】(1)设该种商品每次降价的百分率为x,
依题意,得200(1-x)2=162,
解得x1=0.1=10%,x2=1.9(不合题意,舍去).
∴该种商品每次降价的百分率为10%.
(2)设每件商品应降价y元,根据题意,得
(200-156-y)(20+5y)-150=1 450,
解方程得y1=4,y2=36.
∵降价幅度不超过10元,
∴y=36不合题意,舍去.
∴每件应降价4元.
22.【解】(1)设经过x s,△PBQ的面积等于8 cm2,依题意,
得AP=x cm,BQ=2x cm,∴BP=(6-x)cm.
∴(6-x)·2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2 s或4 s,△PBQ的面积等于8 cm2.
(2)线段PQ不能将△ABC分成面积相等的两部分,
理由如下:
假设经过y s,线段PQ能将△ABC分成面积相等的两部分,依题意,得△ABC的面积=×6×8=24(cm2),
易得(6-y)·2y=24×,
整理,得y2-6y+12=0.
∵Δ=b2-4ac=36-4×12=-12<0,
∴此方程无实数根.
∴线段PQ不能将△ABC分成面积相等的两部分.
(3)①点P在线段AB上,点Q在线段CB上.
设经过m s,依题意易得
(6-m)(8-2m)=1(0<m≤4),
整理,得m2-10m+23=0,
解得m1=5+,m2=5-.
经检验,m1=5+不符合题意,舍去,
∴m=5-;
②点P在线段AB上,点Q在射线CB上(B点下边),
设经过n s,依题意易得
(6-n)(2n-8)=1(4<n≤6),
整理,得n2-10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意;
③点P在射线AB上(B点右边),点Q在射线CB上(B点下边),设经过k s,依题意易得
(k-6)(2k-8)=1(k>6),
整理,得k2-10k+23=0,
解得k1=5+,k2=5-,
经检验,k2=5-不符合题意,舍去,
∴k=5+.
综上所述,经过(5-)s或5 s或(5+)s,
△PBQ的面积为1 cm2.
一、选择题(共10小题,每小题3分,共30分)
1.下列方程中,关于x的一元二次方程是( )
A.2(x2+2x)=2x2-1 B.ax2+bx+c=0
C.(x+1)2=2x+1 D.+x+1=0
2.如果关于x的方程(x-9)2=m+4可以用直接开平方法求解,那么m的取值范围是( )
A.m>3 B.m≥3 C.m>-4 D.m≥-4
3.将一元二次方程2x2-6x+1=0配方,得(x+h)2=k,则h,k的值分别为( )
A.3、8 B.-3、8 C.、 D.-、
4.[2024北京海淀区月考]在下列方程中,有一个方程有两个实数根,且它们互为相反数,这个方程是( )
A.x-1=0 B.x2+x=0 C.x2-1=0 D.x2+1=0
5. 加快推动生态建设步伐,形成“城在林中、园在城中、山水相依、林路相随”的生态格局,市政府计划在某街心公园的一块矩形空地上修建草坪.如图,矩形长为40 m,宽为30 m,在矩形内的四周修筑同样宽的道路,余下的部分(图中阴影部分)铺上草坪.要使草坪的面积为816 m2,道路的宽度应为多少?设矩形地块四周道路的宽度为x m,根据题意,下列方程不正确的是( )
A.1 200-(80x+60x-4x2)=816 B.(40-x)(30-x)=816
C.(40-2x)(30-2x)=816 D.80x+2x(30-2x)=1 200-816
6.[2023威海统考]关于x的一元二次方程x2+ax-6=0的解为x1=2,x2=b,则代数式(2a+b)2 023的值为( )
A.1 B.0 C.-1 D.52 023
7. 如图,四边形ABCD是边长为5的菱形,对角线AC,BD的长度分别是一元二次方程x2+mx+24=0的两个实数根,DH是AB边上的高,则DH的长为( )
A.1.2 B.2.4 C.3.6 D.4.8
8.设x1与x2为一元二次方程x2+2tx-t2=0的两根,则-x1x2+x1+x2+2的最小值为( )
A.1 B.2 C.3 D.4
9. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x](-2≤x<3)的图象如图所示,则方程[x]=x2的解为x=( )
A.0或或2 B.0或 C.1或- D.或-
10.一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中ac≠0,a≠c,给出以下四个结论:①若方程M有两个不相等的实数根,则方程N也有两个不相等的实数根;②若方程M的两根符号相同,则方程N的两根符号也相同;③若m是方程M的一个根,则是方程N的一个根;④若方程M和方程N有一个相同的根,则这个根必是x=1,其中正确的结论是( )
A.①③ B.①②③ C.①②④ D.①③④
二、填空题(共5小题,每小题3分,共15分)
11. 若关于x的一元二次方程(k-1)x2+6x+k2-k=0的一个根是0,则k的值是________.
12.若关于x的一元二次方程x2-6x+k=0有两个不相等的实数根,则k的取值范围是________.
13.一个两位数,其个位上的数与十位上的数的和等于6,而个位与十位上的数的积等于这两位数的三分之一,则这个两位数为________.
14. 《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3.”小聪按此方法解关于x的方程x2+12x+m=0,构造图②,已知阴影部分的面积为60,则该方程的正数解为________.
15.[2024无锡期末]若方程x2-4 096 576=0的两根为x1=2 024, x2=-2 024,则方程x2-2x-4 096 575=0的两根为______________.
三、解答题(共7小题,共75分)
16.(8分)解方程:
(1)x2+2x-3=0; (2)3x(x-2)=8-4x.
17.(8分)[2023廊坊安次区期末]如图,某学校有一块长32米、宽20米的矩形试验田,为了便于管理,现要在中间开辟一横两纵三条等宽的小道,要使种植面积为570平方米,则小道的宽为多少米?
18.(10分)在欧几里得的《几何原本》中,形如x2+ax=b2的一元 二次方程通过图解法能得到其中的一个正根:如图,先画Rt△ACB,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=,连接CD,那么图中某条线段的长就是一元二次方程的其中一个正根.
(1)用含a,b的代数式表示AD的长.
(2)图中哪条线段的长是一元二次方程x2+ax=b2的一个正根?请说明理由.
19.(10分)关于x的一元二次方程a(1-x2)-2bx+c(1+x2)=0中,a,b,c是Rt△ABC的三条边,其中∠C=90°.
(1)求证:此方程有两个不相等的实数根;
(2)若方程的两个根是x1,x2,且x12+x22=12,求a:b:c.
20.(12分) 阅读下列材料,并用相关的思想方法解决问题.材料:为解方程x4-x2-6=0,可将方程变形为(x2)2-x2-6=0,然后设x2=y,则(x2)2=y2,原方程化为y2-y-6=0…①
解得y1=-2,y2=3,当y1=-2时,x2=-2无意义,舍去;
当y2=3时,x2=3,解得x=±;
所以原方程的解为x1=,x2=-.
问题:(1)在原方程得到方程①的过程中,利用________法达到了降次的目的,体现了________的数学思想;
(2)利用以上学习到的方法解方程(x2+5x+1)(x2+5x+7)=7.
21.(12分)某种商品的标价为200元/件,经过两次降价后的价格为162元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为156元/件,以200元/件的价格售出,平均每天能售出20件,另外每天需支付其他各种费用150元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出 5件,如果每天盈利1 450元,每件应降价多少元?
22.(15分) 如图所示,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.
(1)点P从点A开始沿AB边向B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒,△PBQ的面积等于8 cm2
(2)在(1)的基础上,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点P沿射线AB方向从点A出发以1 cm/s的速度移动,同时点Q沿射线CB方向从C点出发以2 cm/s的速度移动,经过几秒,△PBQ的面积为1 cm2
INCLUDEPICTURE"章3.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章3.EPS" \* MERGEFORMATINET 答案
一、1.C 2.D 3.D 4.C 5.B
6.C 【点拨】将x1=2代入x2+ax-6=0,得22+2a-6=0,
解得a=1,
∴关于x的一元二次方程为x2+x-6=0,
解得x1=2,x2=-3,即b=-3.
将a=1,b=-3代入(2a+b)2 023,
得(2a+b)2 023=[2×1+(-3)]2 023=(-1)2 023=-1,
故选C.
7.B 【点拨】∵四边形ABCD是边长为5的菱形,DH是AB边上的高,
∴S菱形ABCD=AC·BD=AB·DH,AB=5.
∴AC·BD=5DH.
∵对角线AC,BD的长度分别是一元二次方程x2+mx+24=0的两实数根,
∴AC·BD=x1·x2==24.
∴×24=5DH.
∴DH==2.4.
故选B.
8.A 【点拨】根据题意,得x1x2=-t2,x1+x2=-2t,
则-x1x2+x1+x2+2=t2-2t+2=(t-1)2+1.
∵(t-1)2≥0,
∴(t-1)2+1≥1.
∴-x1x2+x1+x2+2的最小值为1.
故选A.
9.A 【点拨】当2≤x<3时,x2=2,
解得x1=2,x2=-2(舍去);
当1≤x<2时,x2=1,
解得x1=,x2=-(舍去);
当0≤x<1时,x2=0,解得x=0;
当-1≤x<0时,x2=-1,方程没有实数解;
当-2≤x<-1时,x2=-2,方程没有实数解,
∴方程[x]=x2的解为x=0或x=或x=2.
故选A.
10.B 【点拨】∵M:ax2+bx+c=0有两个不相等的实数根,
∴Δ=b2-4ac>0.
∵N:cx2+bx+a=0的判别式为Δ=b2-4ca=b2-4ac>0,
∴方程N也有两个不相等的实数根,故①正确;
∵M:ax2+bx+c=0的两根符号相同,
∴Δ=b2-4ac≥0,>0.
∴Δ=b2-4ac≥0, >0.
∴方程N的两根符号也相同,故②正确;
∵m是方程M:ax2+bx+c=0的一个根,
∴am2+bm+c=0.
∵+b×+a==0,
∴是方程N的一个根,故③正确;
设方程M和方程N相同的根为x0,
根据题意,得ax02+bx0+c=0,cx02+bx0+a=0,
∴(a-c)x02=a-c.
∵ac≠0,a≠c,
∴x02=1,解得x0=±1,
故这个根是x=±1,故④错误;
故选B.
二、11.0 12.k<9
13.24或15 【点拨】设个位上的数为x,
则十位上的数为(6-x),
由题意得,x(6-x)=[10(6-x)+x],
解得x1=4,x2=5.
∴十位上的数为6-4=2或6-5=1.
∴这个两位数是24或15.
14.4-6 【点拨】x2+12x+m=0,
x2+12x=-m.
∵阴影部分的面积为60,
∴x2+12x=60.
设矩形的宽为a,∴4a=12,则a=3.
同理:先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为3x的矩形,得到大正方形的面积为60+32×4=60+36=96,则该方程的正数解为-6=4-6.
15.x1=2 025,x2=-2 023 【点拨】x2-2x-4 096 575=0,
则x2-2x=4 096 575,
∴x2-2x+1=4 096 575+1.
∴(x-1)2=4 096 576.
∴x-1=±2 024.
∴x1=2 025,x2=-2 023.
三、16.【解】(1)原方程变为(x+3)(x-1)=0,
∴x+3=0或x-1=0.
∴x1=-3,x2=1.
(2)原方程变为3x(x-2)+4(x-2)=0,
∴(x-2)(3x+4)=0.
∴x-2=0或3x+4=0.
∴x1=2,x2=-.
17.【解】设小道的宽为x米,则剩余部分可合成长为(32-2x)米,宽为(20-x)米的矩形,
根据题意得(32-2x)(20-x)=570,
整理得x2-36x+35=0,
解得x1=1,x2=35(不符合题意,舍去).
∴小道的宽为1米.
18.【解】(1)∵∠ACB=90°,BC=,AC=b,
∴AB===.
∴AD=AB-BD=-=.
(2)线段AD的长是一元二次方程x2+ax=b2的一个正根.理由如下:
设AD=m,则AB=AD+BD=m+.
在Rt△ABC中,由勾股定理得b2+=,
整理,得m2+am=b2,
∴线段AD的长是一元二次方程x2+ax=b2的一个正根.
19.(1)【证明】关于x的一元二次方程a(1-x2)-2bx+c(1+x2)=0去括号,整理为一般形式为(c-a)x2-2bx+a+c=0,
∴Δ=(-2b)2-4(a+c)(c-a)=4(2b2+a2-c2).
∵a,b,c是Rt△ABC的三条边,其中∠C=90°,
∴b2+a2-c2=0.
∴2b2+a2-c2>0.
∴Δ=4(2b2+a2-c2)>0.
∴此方程有两个不相等的实数根.
(2)【解】∵方程的两个根是x1,x2,
∴x1+x2=-,x1x2=.
∵x12+x22=12,
∴(x1+x2)2-2x1x2=12,即-=12.
∵b2=c2-a2,∴-=12.
∴-=12.
∴=12.
∴c+a=2c-2a.
∴3a=c.
∴b2=8a2.
∴b=2a.
∴a:b:c=1:2:3.
20.【解】(1)换元;化归
(2)令y=x2+5x,
则原方程化为(y+1)(y+7)=7,
整理,得y2+8y=0,
解得y1=0,y2=-8.
当y=0时,x2+5x=0,
解得x1=0,x2=-5;
当y=-8时,x2+5x=-8,即x2+5x+8=0.
∵Δ=52-4×1×8=-7<0,
∴此方程无实数解.
综上,方程(x2+5x+1)(x2+5x+7)=7的解
为x1=0,x2=-5.
21.【解】(1)设该种商品每次降价的百分率为x,
依题意,得200(1-x)2=162,
解得x1=0.1=10%,x2=1.9(不合题意,舍去).
∴该种商品每次降价的百分率为10%.
(2)设每件商品应降价y元,根据题意,得
(200-156-y)(20+5y)-150=1 450,
解方程得y1=4,y2=36.
∵降价幅度不超过10元,
∴y=36不合题意,舍去.
∴每件应降价4元.
22.【解】(1)设经过x s,△PBQ的面积等于8 cm2,依题意,
得AP=x cm,BQ=2x cm,∴BP=(6-x)cm.
∴(6-x)·2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2 s或4 s,△PBQ的面积等于8 cm2.
(2)线段PQ不能将△ABC分成面积相等的两部分,
理由如下:
假设经过y s,线段PQ能将△ABC分成面积相等的两部分,依题意,得△ABC的面积=×6×8=24(cm2),
易得(6-y)·2y=24×,
整理,得y2-6y+12=0.
∵Δ=b2-4ac=36-4×12=-12<0,
∴此方程无实数根.
∴线段PQ不能将△ABC分成面积相等的两部分.
(3)①点P在线段AB上,点Q在线段CB上.
设经过m s,依题意易得
(6-m)(8-2m)=1(0<m≤4),
整理,得m2-10m+23=0,
解得m1=5+,m2=5-.
经检验,m1=5+不符合题意,舍去,
∴m=5-;
②点P在线段AB上,点Q在射线CB上(B点下边),
设经过n s,依题意易得
(6-n)(2n-8)=1(4<n≤6),
整理,得n2-10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意;
③点P在射线AB上(B点右边),点Q在射线CB上(B点下边),设经过k s,依题意易得
(k-6)(2k-8)=1(k>6),
整理,得k2-10k+23=0,
解得k1=5+,k2=5-,
经检验,k2=5-不符合题意,舍去,
∴k=5+.
综上所述,经过(5-)s或5 s或(5+)s,
△PBQ的面积为1 cm2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
