北师大版数学九年级上册第六章 反比例函数综合素质评价(含答案)
文档属性
| 名称 | 北师大版数学九年级上册第六章 反比例函数综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 611.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 20:51:42 | ||
图片预览



文档简介
第六章综合素质评价
一、选择题(共10小题,每小题3分,共30分)
1.已知反比例函数y=,则下列描述正确的是( )
A.图象位于第二、四象限内 B.图象必经过点
C.图象必经过点 D.y随x的增大而减小
2.已知反比例函数y=(k≠0)的图象经过点(2,3),那么该反比例函数的图象也一定经过点( )
A.(3,2) B.(1,4) C. D.(2,-3)
3.[2023济南]已知点A(-4,y1),B(-2,y2),C(3,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系为( )
A.y3<y2<y1 B.y1<y3<y2 C.y3<y1<y2 D.y2<y3<y1
4.已知甲、乙两地相距40千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B.t= C.t= D.t=
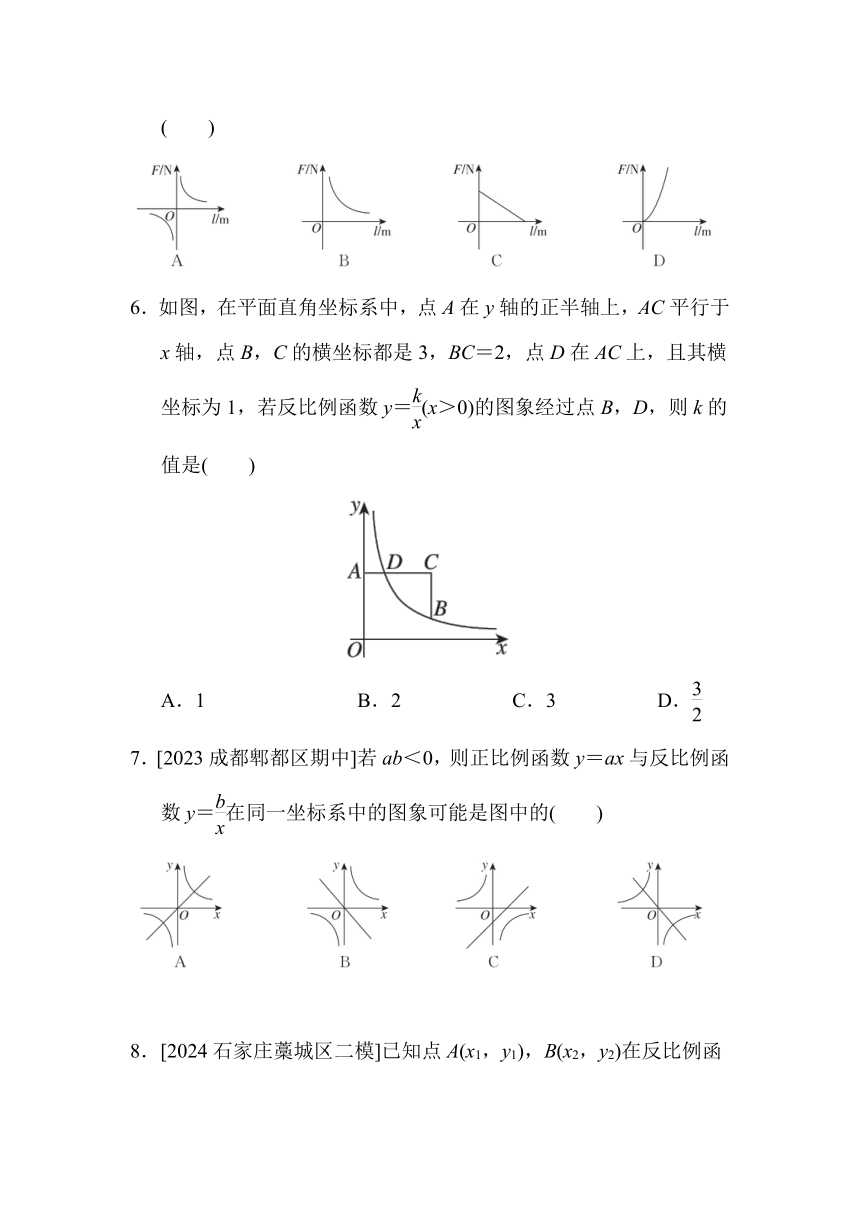
5. 阿基米德说:“给我一个支点,我就能撬动整个地球”这句话阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1 200 N和 0.5 m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
6.如图,在平面直角坐标系中,点A在y轴的正半轴上,AC平行于x轴,点B,C的横坐标都是3,BC=2,点D在AC上,且其横坐标为1,若反比例函数y=(x>0)的图象经过点B,D,则k的值是( )
A.1 B.2 C.3 D.
7.[2023成都郫都区期中]若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的图象可能是图中的( )
8.[2024石家庄藁城区二模]已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,当x1<x2<0时,y1>y2,则m的取值范围为( )
A.m> B.m< C.m> D.m<
9.[2024济宁任城区期末]如图,在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC:OC=1:2,则k的值为( )
A.-3 B.- C.3 D.
10. 一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻R2,R2与踏板上人的质量m之间的函数关系式为 R2=-2m+240(0≤m≤120),其图象如图①所示;图②的电路中,电源电压恒为12 V,定值电阻R1的阻值为60 Ω,接通开关,人站上踏板,电流表显示的读数为I A,该读数可以换算为人的质量m,电流表量程为0~0.2 A(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I=),则下面结论错误的为( )
A.用含I的代数式表示m为m=150-
B.电子秤可称的最大质量为120 kg
C.当m=115 kg时,若电源电压U为12 V,则定值电阻R1最小为70 Ω
D.当m=115 kg时,若定值电阻R1为40 Ω,则电源电压U最大为10 V
二、填空题(共5小题,每小题3分,共15分)
11.若y是x的反比例函数,且x=2时,y=7,则y与x之间的函数关系式是y=________.
12.已知反比例函数y=,当x>3时,y的取值范围是________.
13.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p(kPa)与汽缸内气体的体积V(mL)成反比例关系,p关于V的函数图象如图所示.若压强由75 kPa加压到100 kPa,则气体体积压缩了________mL.
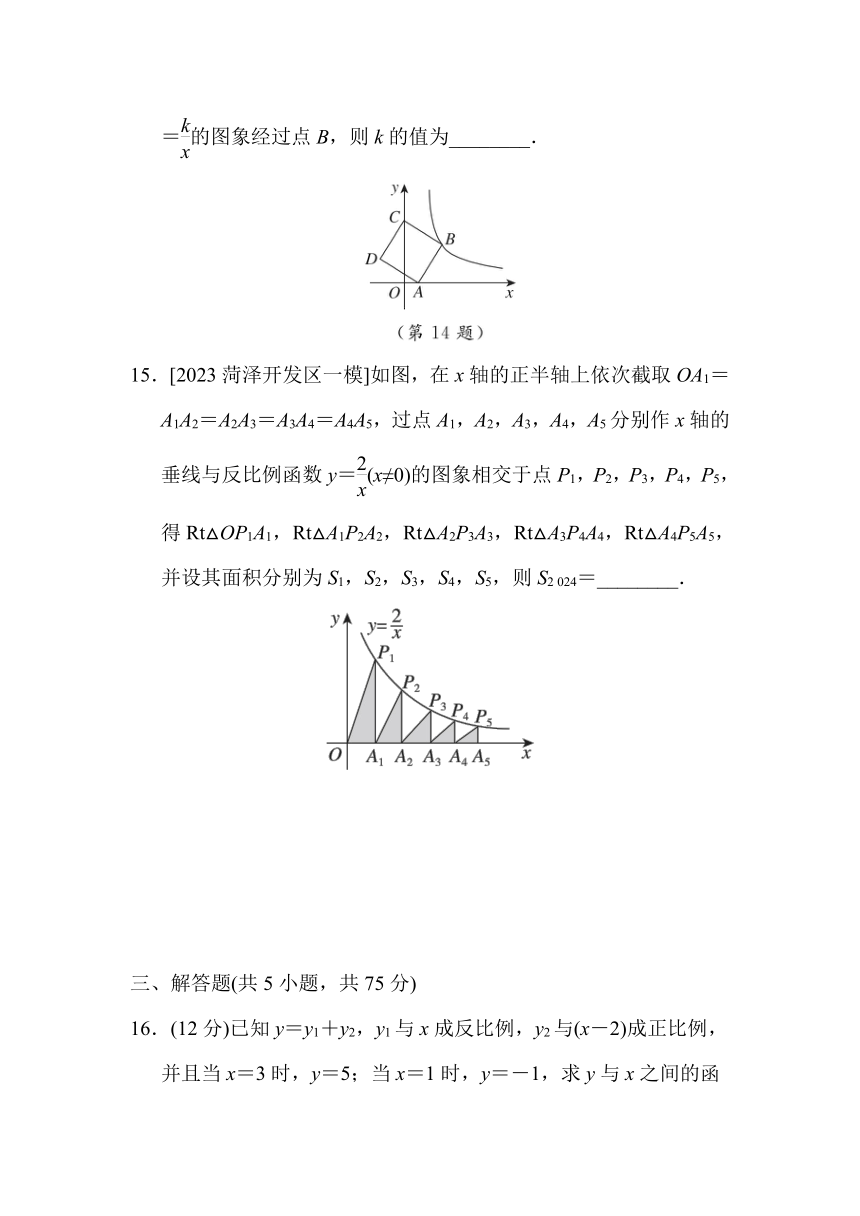
14.如图,在平面直角坐标系中,正方形ABCD的顶点A,C分别在x轴和y轴的正半轴上,点A(1,0),点C(0,5),反比例函数y=的图象经过点B,则k的值为________.
15.[2023菏泽开发区一模]如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1,A2,A3,A4,A5分别作x轴的垂线与反比例函数y=(x≠0)的图象相交于点P1,P2,P3,P4,P5,得Rt△OP1A1,Rt△A1P2A2,Rt△A2P3A3,Rt△A3P4A4,Rt△A4P5A5,并设其面积分别为S1,S2,S3,S4,S5,则S2 024=________.
三、解答题(共5小题,共75分)
16.(12分)已知y=y1+y2,y1与x成反比例,y2与(x-2)成正比例,并且当x=3时,y=5;当x=1时,y=-1,求y与x之间的函数表达式.
17.(14分)为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)满足函数关系式y=2x,药物点燃6分钟后燃尽,药物燃尽后,校医每隔6分钟测一次空气中的含药量,测得数据如下表:
药物点燃后的时间x/分钟 6 12 18 24
空气中的含药量y/(毫克/立方米) 12 6 4 3
(1)在如图所示的平面直角坐标系中描出以表格中数据为坐标的各点;
(2)观察上述各点的分布规律,判断它们是否在同一个反比例函数的图象上,如果在同一个反比例函数的图象上,求出这个反比例函数图象所对应的函数表达式;如果不在同一个反比例函数的图象上,请说明理由;
(3) 研究表明:空气中每立方米的含药量不低于8毫克,且持续 4分钟以上才能有效杀灭空气中的病菌,应用上述发现的规律估算此次消毒能否有效杀灭空气中的病菌.
18.(14分)[2023枣庄]如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=的图象交于A(m,1),B(-2,n)两点.
(1)求一次函数的表达式,并在所给的平面直角坐标系中画出这个 一次函数的图象;
(2)观察图象,直接写出不等式kx+b<的解集;
(3)设直线AB与x轴交于点C,若P(0,a)为y轴上的一动点,连接AP,CP,当△APC的面积为时,求点P的坐标.
19.(16分)[2023泰州海陵区二模]反比例函数y1=,y2=(n<0)的图象如图所示,P为x轴上不与原点重合的一动点,过点P作AB∥y轴,分别与y1,y2的图象交于A,B两点.
(1)当n=-10时,求S△OAB;
(2)延长BA到点D,使得DA=AB,求在点P的整个运动过程中,点D所形成的函数图象的表达式(用含有n的代数式表示).
20.(19分)[2023盐城盐都区二模]盐城市纺织染整产业园为国家级绿色纺织生产基地,现有一块矩形布料的两边长分别是2米与3米,若把这块矩形布料按照如图①的方式扩大到面积为原来的2倍,设原矩形布料的一边加长a米,另一边加长b米,可得a与b之间的函数关系式为b=-2.某校“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=-2,现对这个函数的图象和性质进行探究,探究过程如下:
(1)如图②,在平面直角坐标系xOy中,请用描点法画出y=-2的图象,并完成如下问题:
①函数y=-2的图象可由函数y=的图象(如图)向左平移______个单位长度,再向下平移______个单位长度得到,其对称中心的坐标为________;
②根据该函数图象指出,当x在什么范围内变化时,y≥-1
(2)若要使面积扩大到原来的2倍后这块布料的周长最小,请你帮助该校“数学兴趣小组”设计出符合要求的方案.
INCLUDEPICTURE"章QM1.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章QM1.EPS" \* MERGEFORMATINET
答案
一、1.C 2.A 3.C 4.C 5.B 6.C 7.B 8.D
9.A 【点拨】如图,过点C作CD⊥x轴于点D.
∵=,∴=.
∵BA⊥x轴,CD⊥x轴,
∴CD∥AB.
∴易得△DOC∽△AOB.
∴===.
又∵S△AOB=,
∴S△DOC=S△AOB=×=.∵双曲线y=在第二象限内,∴k=-=-3.故选A.
10.C 【点拨】由题意得I===,变形得m=150-,
∴A选项正确,不符合题意.
由m=150-得m随I的增大而增大.
∵0≤I≤0.2,∴当I=0.2时,m取得最大值120.
∴B选项正确,不符合题意.
当m=115时,R2=10.
∴当U=12时,I==.
∵12>0,∴I随R1的增大而减小.
又∵0≤I≤0.2,
∴当I=0.2时,R1取得最小值50.
∴C选项错误,符合题意.
∵当m=115时,R2=10,
∴U=(R1+R2)I=(40+10)I=50I.
∵50>0,∴U随I的增大而增大.
∵0≤I≤0.2,
∴当I=0.2时,U的值最大,最大值为10.
∴D选项正确,不符合题意.故选C.
二、11. 12.0<y<2 13.20
14.9 【点拨】如图,过点B分别作BE⊥x轴于点E,BF⊥y轴于点F,则∠AEB=∠CFB=∠EBF=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°.
∴∠EBF=∠ABC.
∴∠ABE=∠CBF.
在△ABE和△CBF中,
∴△ABE≌△CBF(AAS).
∴BE=BF,AE=CF.
∴易得四边形OEBF是正方形.
设正方形OEBF的边长为m.
∵点A(1,0),点C(0,5),∴OA=1,OC=5.
∴AE=m-1,CF=5-m.
∴m-1=5-m.
∴m=3.∴B(3,3).
∵反比例函数y=的图象经过点B,
∴k=3×3=9.
15. 【点拨】设OA1=A1A2=A2A3=A3A4=A4A5=m,则P1,P2,P3,P4(4m,),P5,
∴P1A1=,P2A2=,P3A3=,P4A4=,P5A5=.
∴S1=×m·=1,S2=×m·=,
S3=×m·=,S4=×m·=,
S5=×m·=.
由此可得S2 024=×m·=.
三、16.【解】设y1=(m≠0),y2=k(x-2)(k≠0),
则y=y1+y2=+k(x-2).
由题意得解得
∴y与x之间的函数表达式为y=+4(x-2)=+4x-8.
17.【解】(1)如图所示.
(2)观察各点的分布规律,易得它们在同一个反比例函数的图象上.
设反比例函数的表达式为y=,
把点(6,12)的坐标代入,得k=12×6=72,
∴这个反比例函数的表达式为y=.
(3)把y=8代入y=2x,得8=2x,
∴x=4.
把y=8代入y=,得=8,∴x=9.
∵9-4=5(分钟)>4分钟,
∴此次消毒能有效杀灭空气中的病菌.
18.【解】(1)∵反比例函数y=的图象经过A(m,1),B(-2,n)两点,
∴m=4,n==-2.
∴A(4,1),B(-2,-2).
将A(4,1),B(-2,-2)的坐标分别代入y=kx+b,
得解得
∴一次函数的表达式为y=x-1.该函数的图象如图所示.
(2)由图可得,不等式kx+b<的解集是x<-2或0<x<4.
(3)设直线AB交y轴于点D,如图.
在y=x-1中,当x=0时,y=-1,
∴D(0,-1).
当y=0时,x-1=0,解得x=2,
∴C(2,0).∴OC=2.
∵P(0,a),D(0,-1),
∴PD=|a+1|.
易证S△APC=S△PDC.
∵S△APC=,∴|a+1|·2=,
解得a=或-.
∴点P的坐标为或.
19.【解】(1)当n=-10时,y2=-,
∴S△BOP=×|-10|=5.
∵点A在y1=的图象上,
∴S△AOP=×8=4.
∴S△OAB=S△BOP+S△AOP=9.
(2)设P(m,0),则A,B,
∴AB==AD,AP=.
当m>0时,AD=,AP=,
∴DP=AD+AP=+=.∴D.
设x=m,y=,则xy=16-n,
∴y=,即点D所形成的函数图象的表达式为y=;
当m<0时,AD=,AP=-.
同理可得y=.
综上所述,点D所形成的函数图象的表达式为y=.
20.【解】(1)y=-2的图象略.
①3;2;(-3,-2)
②当y=-1时,-1=-2,∴x=9.
由图象可得,当-3<x≤9时,y≥-1.
(2)面积扩大到原来的2倍后这块布料的周长=2(a+3)+2(b+2)=2(a+3)+(米).
∵2(a+3),都为正数,
∴≥0,
∴2(a+3)+-2≥0,
即2(a+3)+≥8.
故当2(a+3)=,即a=2-3(负值已舍去)时,这块布料的周长最小,此时b=2-2.
2-3+3=2(米),
2-2+2=2(米).故将原矩形布料的边长均扩大到2米时,这块布料的周长最小.
一、选择题(共10小题,每小题3分,共30分)
1.已知反比例函数y=,则下列描述正确的是( )
A.图象位于第二、四象限内 B.图象必经过点
C.图象必经过点 D.y随x的增大而减小
2.已知反比例函数y=(k≠0)的图象经过点(2,3),那么该反比例函数的图象也一定经过点( )
A.(3,2) B.(1,4) C. D.(2,-3)
3.[2023济南]已知点A(-4,y1),B(-2,y2),C(3,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系为( )
A.y3<y2<y1 B.y1<y3<y2 C.y3<y1<y2 D.y2<y3<y1
4.已知甲、乙两地相距40千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B.t= C.t= D.t=
5. 阿基米德说:“给我一个支点,我就能撬动整个地球”这句话阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1 200 N和 0.5 m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
6.如图,在平面直角坐标系中,点A在y轴的正半轴上,AC平行于x轴,点B,C的横坐标都是3,BC=2,点D在AC上,且其横坐标为1,若反比例函数y=(x>0)的图象经过点B,D,则k的值是( )
A.1 B.2 C.3 D.
7.[2023成都郫都区期中]若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的图象可能是图中的( )
8.[2024石家庄藁城区二模]已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,当x1<x2<0时,y1>y2,则m的取值范围为( )
A.m> B.m< C.m> D.m<
9.[2024济宁任城区期末]如图,在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC:OC=1:2,则k的值为( )
A.-3 B.- C.3 D.
10. 一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻R2,R2与踏板上人的质量m之间的函数关系式为 R2=-2m+240(0≤m≤120),其图象如图①所示;图②的电路中,电源电压恒为12 V,定值电阻R1的阻值为60 Ω,接通开关,人站上踏板,电流表显示的读数为I A,该读数可以换算为人的质量m,电流表量程为0~0.2 A(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I=),则下面结论错误的为( )
A.用含I的代数式表示m为m=150-
B.电子秤可称的最大质量为120 kg
C.当m=115 kg时,若电源电压U为12 V,则定值电阻R1最小为70 Ω
D.当m=115 kg时,若定值电阻R1为40 Ω,则电源电压U最大为10 V
二、填空题(共5小题,每小题3分,共15分)
11.若y是x的反比例函数,且x=2时,y=7,则y与x之间的函数关系式是y=________.
12.已知反比例函数y=,当x>3时,y的取值范围是________.
13.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p(kPa)与汽缸内气体的体积V(mL)成反比例关系,p关于V的函数图象如图所示.若压强由75 kPa加压到100 kPa,则气体体积压缩了________mL.
14.如图,在平面直角坐标系中,正方形ABCD的顶点A,C分别在x轴和y轴的正半轴上,点A(1,0),点C(0,5),反比例函数y=的图象经过点B,则k的值为________.
15.[2023菏泽开发区一模]如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1,A2,A3,A4,A5分别作x轴的垂线与反比例函数y=(x≠0)的图象相交于点P1,P2,P3,P4,P5,得Rt△OP1A1,Rt△A1P2A2,Rt△A2P3A3,Rt△A3P4A4,Rt△A4P5A5,并设其面积分别为S1,S2,S3,S4,S5,则S2 024=________.
三、解答题(共5小题,共75分)
16.(12分)已知y=y1+y2,y1与x成反比例,y2与(x-2)成正比例,并且当x=3时,y=5;当x=1时,y=-1,求y与x之间的函数表达式.
17.(14分)为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)满足函数关系式y=2x,药物点燃6分钟后燃尽,药物燃尽后,校医每隔6分钟测一次空气中的含药量,测得数据如下表:
药物点燃后的时间x/分钟 6 12 18 24
空气中的含药量y/(毫克/立方米) 12 6 4 3
(1)在如图所示的平面直角坐标系中描出以表格中数据为坐标的各点;
(2)观察上述各点的分布规律,判断它们是否在同一个反比例函数的图象上,如果在同一个反比例函数的图象上,求出这个反比例函数图象所对应的函数表达式;如果不在同一个反比例函数的图象上,请说明理由;
(3) 研究表明:空气中每立方米的含药量不低于8毫克,且持续 4分钟以上才能有效杀灭空气中的病菌,应用上述发现的规律估算此次消毒能否有效杀灭空气中的病菌.
18.(14分)[2023枣庄]如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=的图象交于A(m,1),B(-2,n)两点.
(1)求一次函数的表达式,并在所给的平面直角坐标系中画出这个 一次函数的图象;
(2)观察图象,直接写出不等式kx+b<的解集;
(3)设直线AB与x轴交于点C,若P(0,a)为y轴上的一动点,连接AP,CP,当△APC的面积为时,求点P的坐标.
19.(16分)[2023泰州海陵区二模]反比例函数y1=,y2=(n<0)的图象如图所示,P为x轴上不与原点重合的一动点,过点P作AB∥y轴,分别与y1,y2的图象交于A,B两点.
(1)当n=-10时,求S△OAB;
(2)延长BA到点D,使得DA=AB,求在点P的整个运动过程中,点D所形成的函数图象的表达式(用含有n的代数式表示).
20.(19分)[2023盐城盐都区二模]盐城市纺织染整产业园为国家级绿色纺织生产基地,现有一块矩形布料的两边长分别是2米与3米,若把这块矩形布料按照如图①的方式扩大到面积为原来的2倍,设原矩形布料的一边加长a米,另一边加长b米,可得a与b之间的函数关系式为b=-2.某校“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=-2,现对这个函数的图象和性质进行探究,探究过程如下:
(1)如图②,在平面直角坐标系xOy中,请用描点法画出y=-2的图象,并完成如下问题:
①函数y=-2的图象可由函数y=的图象(如图)向左平移______个单位长度,再向下平移______个单位长度得到,其对称中心的坐标为________;
②根据该函数图象指出,当x在什么范围内变化时,y≥-1
(2)若要使面积扩大到原来的2倍后这块布料的周长最小,请你帮助该校“数学兴趣小组”设计出符合要求的方案.
INCLUDEPICTURE"章QM1.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章QM1.EPS" \* MERGEFORMATINET
答案
一、1.C 2.A 3.C 4.C 5.B 6.C 7.B 8.D
9.A 【点拨】如图,过点C作CD⊥x轴于点D.
∵=,∴=.
∵BA⊥x轴,CD⊥x轴,
∴CD∥AB.
∴易得△DOC∽△AOB.
∴===.
又∵S△AOB=,
∴S△DOC=S△AOB=×=.∵双曲线y=在第二象限内,∴k=-=-3.故选A.
10.C 【点拨】由题意得I===,变形得m=150-,
∴A选项正确,不符合题意.
由m=150-得m随I的增大而增大.
∵0≤I≤0.2,∴当I=0.2时,m取得最大值120.
∴B选项正确,不符合题意.
当m=115时,R2=10.
∴当U=12时,I==.
∵12>0,∴I随R1的增大而减小.
又∵0≤I≤0.2,
∴当I=0.2时,R1取得最小值50.
∴C选项错误,符合题意.
∵当m=115时,R2=10,
∴U=(R1+R2)I=(40+10)I=50I.
∵50>0,∴U随I的增大而增大.
∵0≤I≤0.2,
∴当I=0.2时,U的值最大,最大值为10.
∴D选项正确,不符合题意.故选C.
二、11. 12.0<y<2 13.20
14.9 【点拨】如图,过点B分别作BE⊥x轴于点E,BF⊥y轴于点F,则∠AEB=∠CFB=∠EBF=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°.
∴∠EBF=∠ABC.
∴∠ABE=∠CBF.
在△ABE和△CBF中,
∴△ABE≌△CBF(AAS).
∴BE=BF,AE=CF.
∴易得四边形OEBF是正方形.
设正方形OEBF的边长为m.
∵点A(1,0),点C(0,5),∴OA=1,OC=5.
∴AE=m-1,CF=5-m.
∴m-1=5-m.
∴m=3.∴B(3,3).
∵反比例函数y=的图象经过点B,
∴k=3×3=9.
15. 【点拨】设OA1=A1A2=A2A3=A3A4=A4A5=m,则P1,P2,P3,P4(4m,),P5,
∴P1A1=,P2A2=,P3A3=,P4A4=,P5A5=.
∴S1=×m·=1,S2=×m·=,
S3=×m·=,S4=×m·=,
S5=×m·=.
由此可得S2 024=×m·=.
三、16.【解】设y1=(m≠0),y2=k(x-2)(k≠0),
则y=y1+y2=+k(x-2).
由题意得解得
∴y与x之间的函数表达式为y=+4(x-2)=+4x-8.
17.【解】(1)如图所示.
(2)观察各点的分布规律,易得它们在同一个反比例函数的图象上.
设反比例函数的表达式为y=,
把点(6,12)的坐标代入,得k=12×6=72,
∴这个反比例函数的表达式为y=.
(3)把y=8代入y=2x,得8=2x,
∴x=4.
把y=8代入y=,得=8,∴x=9.
∵9-4=5(分钟)>4分钟,
∴此次消毒能有效杀灭空气中的病菌.
18.【解】(1)∵反比例函数y=的图象经过A(m,1),B(-2,n)两点,
∴m=4,n==-2.
∴A(4,1),B(-2,-2).
将A(4,1),B(-2,-2)的坐标分别代入y=kx+b,
得解得
∴一次函数的表达式为y=x-1.该函数的图象如图所示.
(2)由图可得,不等式kx+b<的解集是x<-2或0<x<4.
(3)设直线AB交y轴于点D,如图.
在y=x-1中,当x=0时,y=-1,
∴D(0,-1).
当y=0时,x-1=0,解得x=2,
∴C(2,0).∴OC=2.
∵P(0,a),D(0,-1),
∴PD=|a+1|.
易证S△APC=S△PDC.
∵S△APC=,∴|a+1|·2=,
解得a=或-.
∴点P的坐标为或.
19.【解】(1)当n=-10时,y2=-,
∴S△BOP=×|-10|=5.
∵点A在y1=的图象上,
∴S△AOP=×8=4.
∴S△OAB=S△BOP+S△AOP=9.
(2)设P(m,0),则A,B,
∴AB==AD,AP=.
当m>0时,AD=,AP=,
∴DP=AD+AP=+=.∴D.
设x=m,y=,则xy=16-n,
∴y=,即点D所形成的函数图象的表达式为y=;
当m<0时,AD=,AP=-.
同理可得y=.
综上所述,点D所形成的函数图象的表达式为y=.
20.【解】(1)y=-2的图象略.
①3;2;(-3,-2)
②当y=-1时,-1=-2,∴x=9.
由图象可得,当-3<x≤9时,y≥-1.
(2)面积扩大到原来的2倍后这块布料的周长=2(a+3)+2(b+2)=2(a+3)+(米).
∵2(a+3),都为正数,
∴≥0,
∴2(a+3)+-2≥0,
即2(a+3)+≥8.
故当2(a+3)=,即a=2-3(负值已舍去)时,这块布料的周长最小,此时b=2-2.
2-3+3=2(米),
2-2+2=2(米).故将原矩形布料的边长均扩大到2米时,这块布料的周长最小.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
