北师大版数学九年级上册第四章 图形的相似 综合素质评价(含答案)
文档属性
| 名称 | 北师大版数学九年级上册第四章 图形的相似 综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 662.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 20:54:37 | ||
图片预览


文档简介
第四章综合素质评价
一、选择题(每题3分,共30分)
1.[2023金昌]若=,则ab=( )
A.6 B. C.1 D.
2.下列命题正确的是( )
A.有一个角对应相等的平行四边形都相似
B.对应边成比例的两个平行四边形相似
C.有一个角对应相等的两个等腰梯形相似
D.有一个角对应相等的菱形是相似多边形
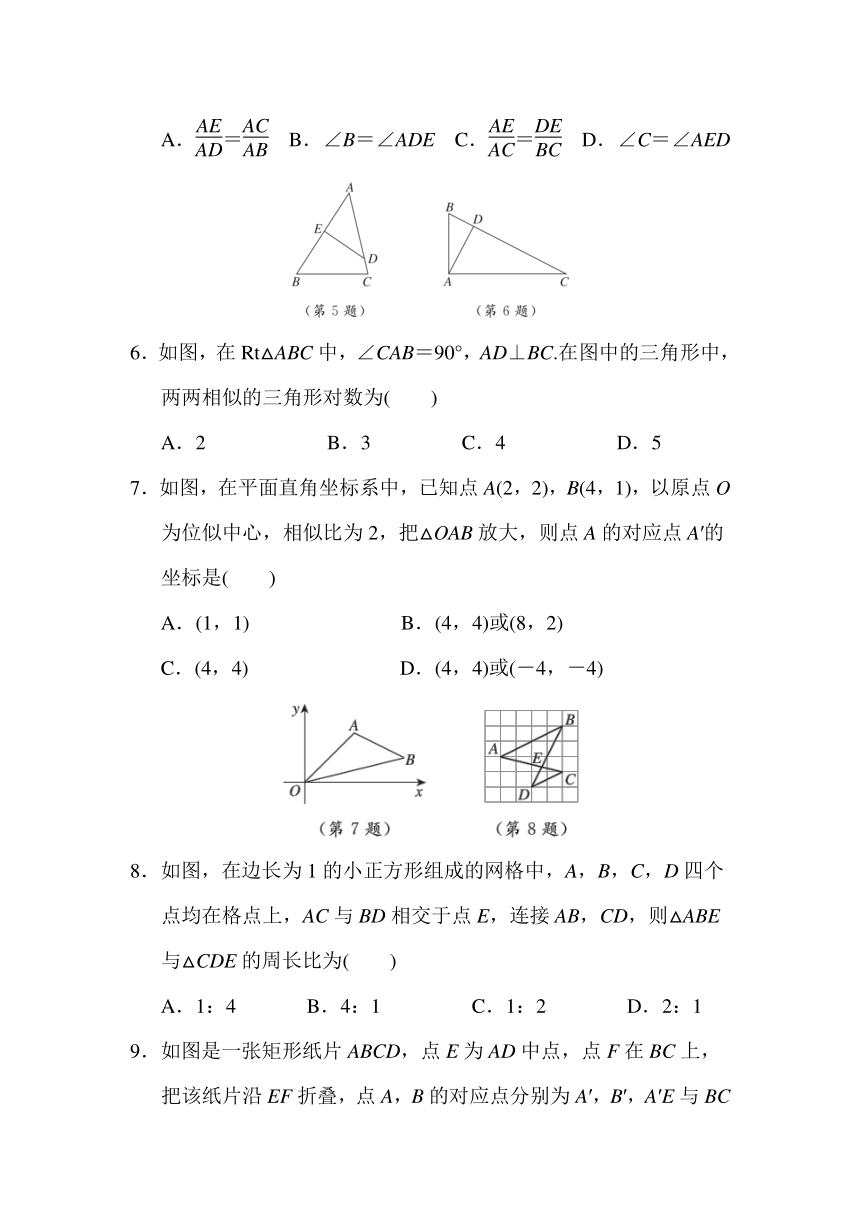
3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )
A.2 B.4 C.6 D.8
4.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上,若线段AB=4,则线段BC的长为( )
A.6 B.8 C.10 D.12
5.如图,由下列条件不能判定△ABC与△ADE相似的是( )
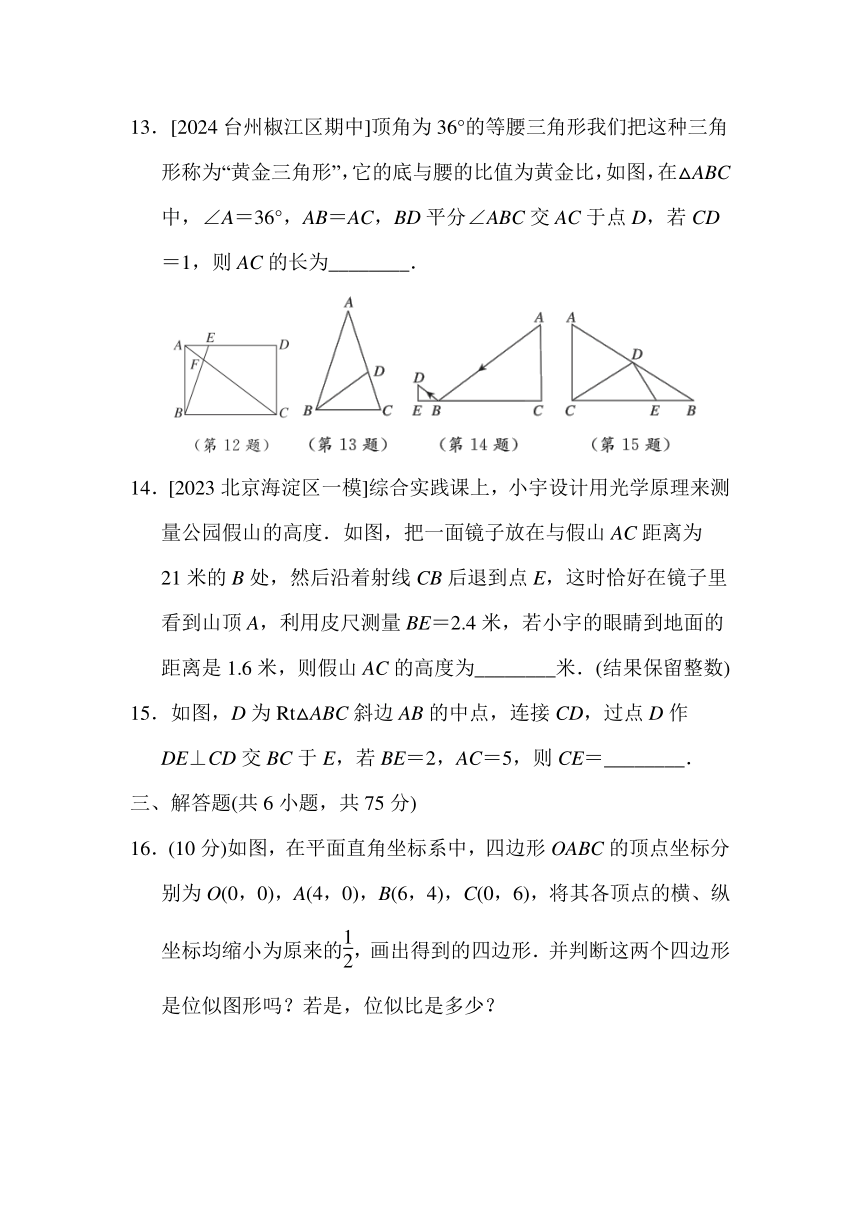
A.= B.∠B=∠ADE C.= D.∠C=∠AED
6.如图,在Rt△ABC中,∠CAB=90°,AD⊥BC.在图中的三角形中,两两相似的三角形对数为( )
A.2 B.3 C.4 D.5
7.如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A′的坐标是( )
A.(1,1) B.(4,4)或(8,2)
C.(4,4) D.(4,4)或(-4,-4)
8.如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD相交于点E,连接AB,CD,则△ABE与△CDE的周长比为( )
A.1:4 B.4:1 C.1:2 D.2:1
9.如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A′,B′,A′E与BC相交于点G,B′A′的延长线过点C.若=,则的值为( )
A.2 B. C. D.
10.如图,在矩形ABCD中,AB=1,BC=2,连接AC,以对角线AC为边,按逆时针方向作矩形ACC1B1,使矩形ACC1B1∽矩形ADCB;再连接AC1,以对角线AC1为边,按逆时针方向作矩形AC1C2B2,使矩形AC1C2B2∽矩形ACC1B1,…,按照此规律作下去,则边AC2 024的长为( )
A.× B.2× C.×22 024 D.×
二、填空题(每题3分,共15分)
11.[2024汉中汉台区期中]如图,四边形ABCD∽四边形A′B′C′D′,则∠D′的度数为________.
12.[2022北京]如图,在矩形ABCD中,若AB=3,AC=5,=,则AE的长为________.
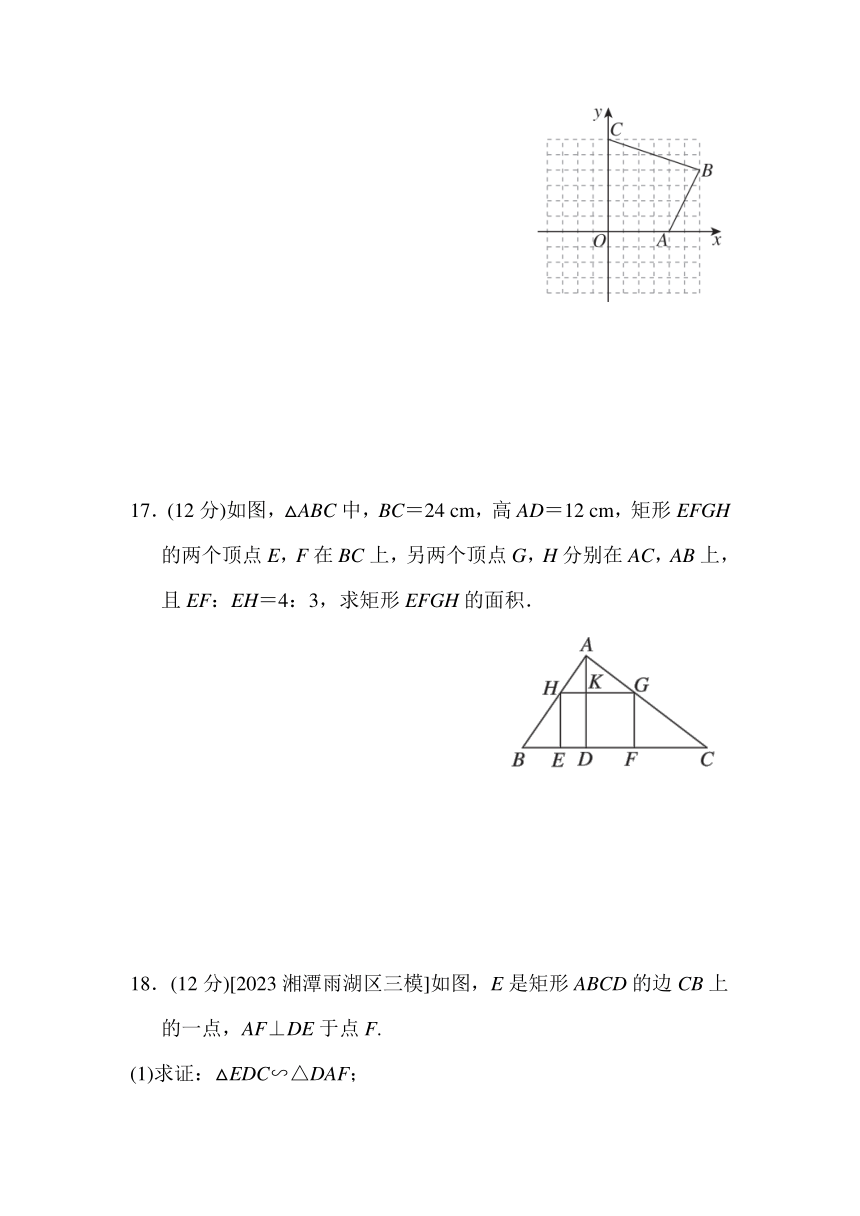
13.[2024台州椒江区期中]顶角为36°的等腰三角形我们把这种三角形称为“黄金三角形”,它的底与腰的比值为黄金比,如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为________.
14.[2023北京海淀区一模]综合实践课上,小宇设计用光学原理来测量公园假山的高度.如图,把一面镜子放在与假山AC距离为 21米的B处,然后沿着射线CB后退到点E,这时恰好在镜子里看到山顶A,利用皮尺测量BE=2.4米,若小宇的眼睛到地面的距离是1.6米,则假山AC的高度为________米.(结果保留整数)
15.如图,D为Rt△ABC斜边AB的中点,连接CD,过点D作 DE⊥CD交BC于E,若BE=2,AC=5,则CE=________.
三、解答题(共6小题,共75分)
16.(10分)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(4,0),B(6,4),C(0,6),将其各顶点的横、纵坐标均缩小为原来的,画出得到的四边形.并判断这两个四边形是位似图形吗?若是,位似比是多少?
17.(12分)如图,△ABC中,BC=24 cm,高AD=12 cm,矩形EFGH的两个顶点E,F在BC上,另两个顶点G,H分别在AC,AB上,且EF:EH=4:3,求矩形EFGH的面积.
18.(12分)[2023湘潭雨湖区三模]如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F.
(1)求证:△EDC∽△DAF;
(2)若AB=3,AD=2,当点E为BC的中点时,求线段EF的长度.
19.(12分)[2024西安灞桥区三模]大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC= 1.28米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.92米,CG=20米,请你根据以上数据,计算古塔的高度AB.
20.(14分)如图,在△ABC中,BA=BC=20 cm,AC=30 cm,点P从A点出发,沿着AB以每秒4 cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3 cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由.
21.(15分)在Rt△ABC中,∠B=90°,AB=4,BC=3,D,E分别是线段BC,AC上的点,且满足==,连接DE,将△CDE绕着点C逆时针旋转,记旋转角为α.
(1)①当α=0°时,=________;
②当α=90°时,=________.
(2)如图②,当0°<α<90°时,过点D作DM⊥BC于点M,过E作EN⊥AC于点N,求出的值;
(3)当0°<α<360°时,若O为DE的中点,求在旋转过程中,线段OB长的最大值和最小值.
INCLUDEPICTURE"章5.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章5.EPS" \* MERGEFORMATINET
答案
一、1.A 2.D 3.C 4.D 5.C 6.B 7.D 8.D
9.A 【点拨】解法一:过点G作GT⊥AD于点T.
设AB=x,AD=y.
∵=,∴设BF=2k,CG=3k.
∵AE=DE=y,由翻折的性质可知EA=EA′=y,
BF=FB′=2k,∠AEF=∠GEF.
∵AD∥CB,∴∠AEF=∠EFG.
∴∠GEF=∠GFE.∴EG=FG=y-5k.
∴GA′=y-(y-5k)=5k-y.
∵C,A′,B′共线,GA′∥FB′,∴=.
易得CF=y-2k.
∴=.
∴y2-12ky+32k2=0.
∴y=8k或y=4k(舍去).
∴AE=DE=4k.
易得四边形CDTG是矩形,∴CG=DT=3k.
∴ET=k.
∵EG=8k-5k=3k,
∴AB=CD=GT==2k.
∴==2.
解法二:不妨设BF=2,CG=3,连接CE,则Rt△CA′E≌Rt△CDE,推出A′C=CD=AB=A′B′,推出==1,推出GF=CG=3,推出BC=AD=8.
在Rt△CB′F中,由勾股定理得CB′=4,
则A′B′=AB=2,则==2.故选A.
10.A 【点拨】∵四边形ABCD是矩形,
∴AB⊥BC.∴AC===.
∵按逆时针方向作矩形ABCD的相似矩形ACC1B1,
∴矩形ACC1B1的边长和矩形ABCD的相似比为:2.
∴矩形ACC1B1的对角线和矩形ABCD的对角线的比为:2.
∵矩形ABCD的对角线长为,
∴矩形AB1C1C的对角线AC1=×=,
依此类推,矩形AB2C2C1的对角线和矩形AB1C1C的对角线的比为:2,
∴矩形AB2C2C1的对角线AC2=×.
∴矩形AB3C3C2的对角线AC3=×,
按此规律第n个矩形的对角线ACn=×,
∴AC2 024的长为×,故选A.
二、11.48° 12.1 13. 14.14
15. 【点拨】如图,取CE的中点为F,连接DF.
∵DE⊥CD,∴DF=CF=EF.
∴∠FCD=∠FDC.
∵∠ACB=90°,D是AB上的中点,
∴AD=BD=CD.∴∠DCF=∠B.
∴△FCD∽△DCB.∴=.
设CF=x,CD=a,
则DF=EF=x,BD=AD=a,
∴BC=2x+2.∴=.
∴a2=2x+2x2.
在Rt△ABC中,AC2+BC2=AB2,
∴52+(2x+2)2=(2a)2.
∴4x2+8x+29=4a2.
∴4x2+8x+29=4(2x+2x2),
解得x=(负值已舍去).
∴CE=2x=.
三、16.【解】如图,四边形OA′B′C′即为所画的四边形.
由题易得四边形OA′B′C′与四边形OABC是相似图形,且对应点的连线都经过同一点O,对应边平行,
∴四边形OA′B′C′与四边形OABC是位似图形,位似比为.
17.【解】设EF=4k,EH=3k,则AK=12-3k,GH=4k.
∵HG∥BC,∴∠AHG=∠ABC,∠AGH=∠ACB.
∴△AHG∽△ABC.
∴=,即=.
解得k=2.4 cm.
∴EF=4×2.4=9.6(cm),HE=2.4×3=7.2(cm).
∴S矩形EFGH=EF·EH=9.6×7.2=69.12(cm2).
18.(1)【证明】∵AF⊥DE,四边形ABCD是矩形,
∴∠AFD=90°=∠C,∠ADF+∠DAF=90°,∠ADC=90°.
∴∠ADF+∠EDC=90°.
∴∠EDC=∠DAF.∴△EDC∽△DAF.
(2)【解】∵四边形ABCD是矩形,
∴DC=AB=3,∠ADC=∠C=90°,BC=AD=2.
∵点E为BC的中点,∴CE=1.
∴DE==.
∵△EDC∽△DAF,
∴=,即=.
∴FD=.
∴EF=DE-DF=-=.
19.【解】根据题意得△EDC∽△EBA,△FHG∽△FBA,
∴=,=.
∵CD=GH,∴=.
∴=,
解得CA=40米.
∵=,∴=,
解得AB=64.5米.
因此,古塔的高度AB为64.5米.
20.【解】(1)由题意得,AP=4x cm,BP=(20-4x) cm,CQ=3x cm,
AQ=(30-3x)cm.
当PQ∥BC时,=.
∴=,即=.
整理得50-15x=0.∴x=.
∴当x=时,PQ∥BC.
(2)存在.
∵BA=BC,∴∠A=∠C.
则当=时,△APQ∽△CQB.
∵=,∴=.
整理得9x2-10x=0.
∴x1=0(不合题意舍去),x2=.
当x=时,AP= cm.
21.【解】(1)① ②
(2)如图①,连接AE,BD.
∵∠BCA=∠DCE,∴∠BCD=∠ACE.
又∵==,∴△BCD∽△ACE.
∴∠CBD=∠CAE,==.
∵∠CBD=∠CAE,∠DMB=∠ENA=90°,
∴△BDM∽△AEN.∴==.
(3)如图②,连接OC.
∵CD=2,CE=,∴DE==.
∵O是DE的中点,∴DO=DE=.
∴CO===.
∴当0°<α<360°时,在旋转过程中,
当点O在线段BC上时,线段OB长的最小值为3-;
当点O在线段BC延长线上时,
线段OB长的最大值为3+.
一、选择题(每题3分,共30分)
1.[2023金昌]若=,则ab=( )
A.6 B. C.1 D.
2.下列命题正确的是( )
A.有一个角对应相等的平行四边形都相似
B.对应边成比例的两个平行四边形相似
C.有一个角对应相等的两个等腰梯形相似
D.有一个角对应相等的菱形是相似多边形
3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )
A.2 B.4 C.6 D.8
4.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上,若线段AB=4,则线段BC的长为( )
A.6 B.8 C.10 D.12
5.如图,由下列条件不能判定△ABC与△ADE相似的是( )
A.= B.∠B=∠ADE C.= D.∠C=∠AED
6.如图,在Rt△ABC中,∠CAB=90°,AD⊥BC.在图中的三角形中,两两相似的三角形对数为( )
A.2 B.3 C.4 D.5
7.如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A′的坐标是( )
A.(1,1) B.(4,4)或(8,2)
C.(4,4) D.(4,4)或(-4,-4)
8.如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD相交于点E,连接AB,CD,则△ABE与△CDE的周长比为( )
A.1:4 B.4:1 C.1:2 D.2:1
9.如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A′,B′,A′E与BC相交于点G,B′A′的延长线过点C.若=,则的值为( )
A.2 B. C. D.
10.如图,在矩形ABCD中,AB=1,BC=2,连接AC,以对角线AC为边,按逆时针方向作矩形ACC1B1,使矩形ACC1B1∽矩形ADCB;再连接AC1,以对角线AC1为边,按逆时针方向作矩形AC1C2B2,使矩形AC1C2B2∽矩形ACC1B1,…,按照此规律作下去,则边AC2 024的长为( )
A.× B.2× C.×22 024 D.×
二、填空题(每题3分,共15分)
11.[2024汉中汉台区期中]如图,四边形ABCD∽四边形A′B′C′D′,则∠D′的度数为________.
12.[2022北京]如图,在矩形ABCD中,若AB=3,AC=5,=,则AE的长为________.
13.[2024台州椒江区期中]顶角为36°的等腰三角形我们把这种三角形称为“黄金三角形”,它的底与腰的比值为黄金比,如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为________.
14.[2023北京海淀区一模]综合实践课上,小宇设计用光学原理来测量公园假山的高度.如图,把一面镜子放在与假山AC距离为 21米的B处,然后沿着射线CB后退到点E,这时恰好在镜子里看到山顶A,利用皮尺测量BE=2.4米,若小宇的眼睛到地面的距离是1.6米,则假山AC的高度为________米.(结果保留整数)
15.如图,D为Rt△ABC斜边AB的中点,连接CD,过点D作 DE⊥CD交BC于E,若BE=2,AC=5,则CE=________.
三、解答题(共6小题,共75分)
16.(10分)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(4,0),B(6,4),C(0,6),将其各顶点的横、纵坐标均缩小为原来的,画出得到的四边形.并判断这两个四边形是位似图形吗?若是,位似比是多少?
17.(12分)如图,△ABC中,BC=24 cm,高AD=12 cm,矩形EFGH的两个顶点E,F在BC上,另两个顶点G,H分别在AC,AB上,且EF:EH=4:3,求矩形EFGH的面积.
18.(12分)[2023湘潭雨湖区三模]如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F.
(1)求证:△EDC∽△DAF;
(2)若AB=3,AD=2,当点E为BC的中点时,求线段EF的长度.
19.(12分)[2024西安灞桥区三模]大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC= 1.28米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.92米,CG=20米,请你根据以上数据,计算古塔的高度AB.
20.(14分)如图,在△ABC中,BA=BC=20 cm,AC=30 cm,点P从A点出发,沿着AB以每秒4 cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3 cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由.
21.(15分)在Rt△ABC中,∠B=90°,AB=4,BC=3,D,E分别是线段BC,AC上的点,且满足==,连接DE,将△CDE绕着点C逆时针旋转,记旋转角为α.
(1)①当α=0°时,=________;
②当α=90°时,=________.
(2)如图②,当0°<α<90°时,过点D作DM⊥BC于点M,过E作EN⊥AC于点N,求出的值;
(3)当0°<α<360°时,若O为DE的中点,求在旋转过程中,线段OB长的最大值和最小值.
INCLUDEPICTURE"章5.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章5.EPS" \* MERGEFORMATINET
答案
一、1.A 2.D 3.C 4.D 5.C 6.B 7.D 8.D
9.A 【点拨】解法一:过点G作GT⊥AD于点T.
设AB=x,AD=y.
∵=,∴设BF=2k,CG=3k.
∵AE=DE=y,由翻折的性质可知EA=EA′=y,
BF=FB′=2k,∠AEF=∠GEF.
∵AD∥CB,∴∠AEF=∠EFG.
∴∠GEF=∠GFE.∴EG=FG=y-5k.
∴GA′=y-(y-5k)=5k-y.
∵C,A′,B′共线,GA′∥FB′,∴=.
易得CF=y-2k.
∴=.
∴y2-12ky+32k2=0.
∴y=8k或y=4k(舍去).
∴AE=DE=4k.
易得四边形CDTG是矩形,∴CG=DT=3k.
∴ET=k.
∵EG=8k-5k=3k,
∴AB=CD=GT==2k.
∴==2.
解法二:不妨设BF=2,CG=3,连接CE,则Rt△CA′E≌Rt△CDE,推出A′C=CD=AB=A′B′,推出==1,推出GF=CG=3,推出BC=AD=8.
在Rt△CB′F中,由勾股定理得CB′=4,
则A′B′=AB=2,则==2.故选A.
10.A 【点拨】∵四边形ABCD是矩形,
∴AB⊥BC.∴AC===.
∵按逆时针方向作矩形ABCD的相似矩形ACC1B1,
∴矩形ACC1B1的边长和矩形ABCD的相似比为:2.
∴矩形ACC1B1的对角线和矩形ABCD的对角线的比为:2.
∵矩形ABCD的对角线长为,
∴矩形AB1C1C的对角线AC1=×=,
依此类推,矩形AB2C2C1的对角线和矩形AB1C1C的对角线的比为:2,
∴矩形AB2C2C1的对角线AC2=×.
∴矩形AB3C3C2的对角线AC3=×,
按此规律第n个矩形的对角线ACn=×,
∴AC2 024的长为×,故选A.
二、11.48° 12.1 13. 14.14
15. 【点拨】如图,取CE的中点为F,连接DF.
∵DE⊥CD,∴DF=CF=EF.
∴∠FCD=∠FDC.
∵∠ACB=90°,D是AB上的中点,
∴AD=BD=CD.∴∠DCF=∠B.
∴△FCD∽△DCB.∴=.
设CF=x,CD=a,
则DF=EF=x,BD=AD=a,
∴BC=2x+2.∴=.
∴a2=2x+2x2.
在Rt△ABC中,AC2+BC2=AB2,
∴52+(2x+2)2=(2a)2.
∴4x2+8x+29=4a2.
∴4x2+8x+29=4(2x+2x2),
解得x=(负值已舍去).
∴CE=2x=.
三、16.【解】如图,四边形OA′B′C′即为所画的四边形.
由题易得四边形OA′B′C′与四边形OABC是相似图形,且对应点的连线都经过同一点O,对应边平行,
∴四边形OA′B′C′与四边形OABC是位似图形,位似比为.
17.【解】设EF=4k,EH=3k,则AK=12-3k,GH=4k.
∵HG∥BC,∴∠AHG=∠ABC,∠AGH=∠ACB.
∴△AHG∽△ABC.
∴=,即=.
解得k=2.4 cm.
∴EF=4×2.4=9.6(cm),HE=2.4×3=7.2(cm).
∴S矩形EFGH=EF·EH=9.6×7.2=69.12(cm2).
18.(1)【证明】∵AF⊥DE,四边形ABCD是矩形,
∴∠AFD=90°=∠C,∠ADF+∠DAF=90°,∠ADC=90°.
∴∠ADF+∠EDC=90°.
∴∠EDC=∠DAF.∴△EDC∽△DAF.
(2)【解】∵四边形ABCD是矩形,
∴DC=AB=3,∠ADC=∠C=90°,BC=AD=2.
∵点E为BC的中点,∴CE=1.
∴DE==.
∵△EDC∽△DAF,
∴=,即=.
∴FD=.
∴EF=DE-DF=-=.
19.【解】根据题意得△EDC∽△EBA,△FHG∽△FBA,
∴=,=.
∵CD=GH,∴=.
∴=,
解得CA=40米.
∵=,∴=,
解得AB=64.5米.
因此,古塔的高度AB为64.5米.
20.【解】(1)由题意得,AP=4x cm,BP=(20-4x) cm,CQ=3x cm,
AQ=(30-3x)cm.
当PQ∥BC时,=.
∴=,即=.
整理得50-15x=0.∴x=.
∴当x=时,PQ∥BC.
(2)存在.
∵BA=BC,∴∠A=∠C.
则当=时,△APQ∽△CQB.
∵=,∴=.
整理得9x2-10x=0.
∴x1=0(不合题意舍去),x2=.
当x=时,AP= cm.
21.【解】(1)① ②
(2)如图①,连接AE,BD.
∵∠BCA=∠DCE,∴∠BCD=∠ACE.
又∵==,∴△BCD∽△ACE.
∴∠CBD=∠CAE,==.
∵∠CBD=∠CAE,∠DMB=∠ENA=90°,
∴△BDM∽△AEN.∴==.
(3)如图②,连接OC.
∵CD=2,CE=,∴DE==.
∵O是DE的中点,∴DO=DE=.
∴CO===.
∴当0°<α<360°时,在旋转过程中,
当点O在线段BC上时,线段OB长的最小值为3-;
当点O在线段BC延长线上时,
线段OB长的最大值为3+.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
