北师大版数学九年级上册第一章 特殊平行四边形综合素质评价(含答案)
文档属性
| 名称 | 北师大版数学九年级上册第一章 特殊平行四边形综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 753.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 20:56:25 | ||
图片预览


文档简介
第一章综合素质评价
一、选择题(共10小题,每小题3分,共30分)
1.[2023揭阳期末]菱形、矩形、正方形都具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.四条边相等,四个角相等 D.两组对边分别平行且相等
2.[2024邢台襄都区模拟]如图,在四边形ABCD中,给出部分数据,若添加一个数据后,四边形ABCD是矩形,则添加的数据是( )
A.CD=4 B.CD=2 C.OD=2 D.OD=4
3.[2023成都温江区期末]如图,F是正方形ABCD对角线BD上 一点,连接AF,CF,并延长CF交AD于点E.若∠AFC=130°,则∠DEC的度数为( )
A.65° B.70° C.75° D.80°
4.[2022安徽]两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α-90° B.α-45° C.180°-α D.270°-α
5.[2023东莞期中]若顺次连接某四边形四边中点所得的四边形是矩形,则原四边形一定是( )
A.菱形 B.矩形
C.对角线互相垂直的四边形 D.对角线相等的四边形
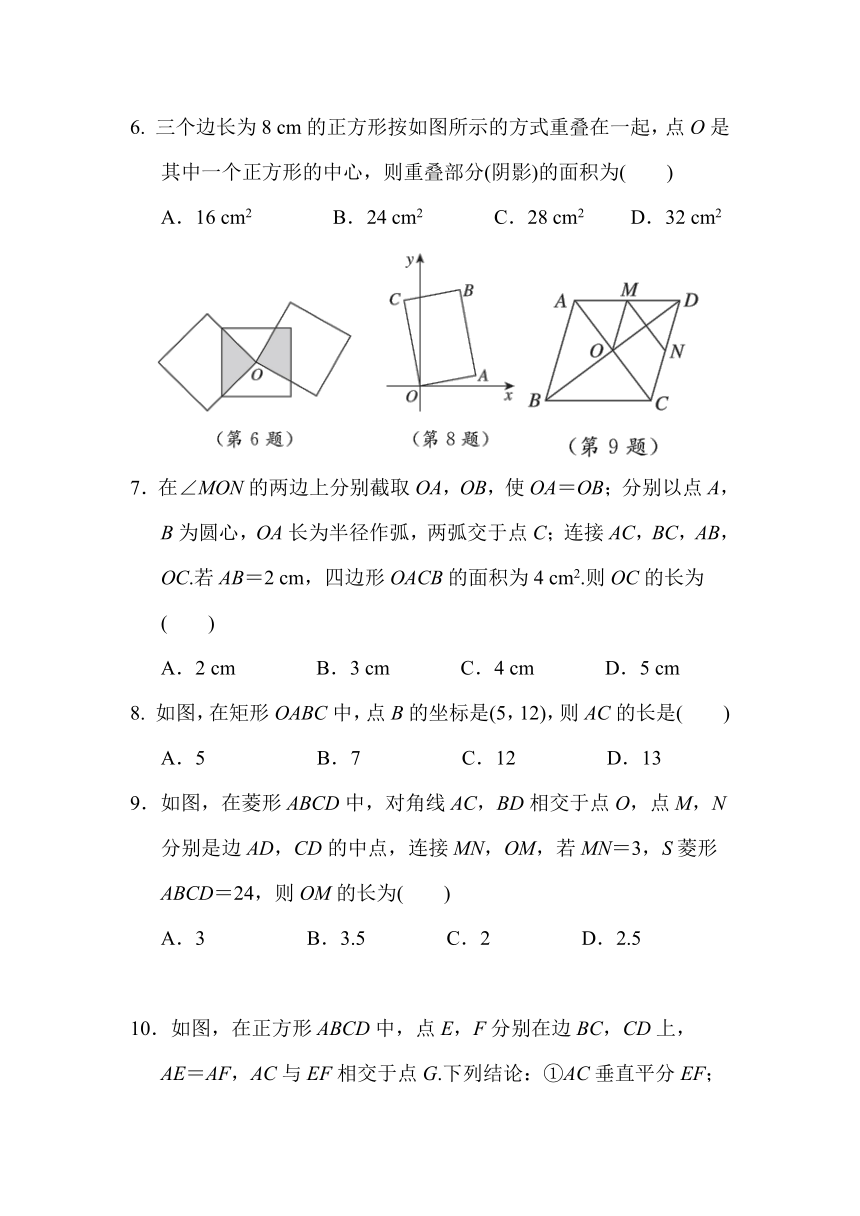
6. 三个边长为8 cm的正方形按如图所示的方式重叠在一起,点O是其中一个正方形的中心,则重叠部分(阴影)的面积为( )
A.16 cm2 B.24 cm2 C.28 cm2 D.32 cm2
7.在∠MON的两边上分别截取OA,OB,使OA=OB;分别以点A,B为圆心,OA长为半径作弧,两弧交于点C;连接AC,BC,AB,OC.若AB=2 cm,四边形OACB的面积为4 cm2.则OC的长为( )
A.2 cm B.3 cm C.4 cm D.5 cm
8. 如图,在矩形OABC中,点B的坐标是(5,12),则AC的长是( )
A.5 B.7 C.12 D.13
9.如图,在菱形ABCD中,对角线AC,BD相交于点O,点M,N分别是边AD,CD的中点,连接MN,OM,若MN=3,S菱形ABCD=24,则OM的长为( )
A.3 B.3.5 C.2 D.2.5
10.如图,在正方形ABCD中,点E,F分别在边BC,CD上, AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②当∠EAF=45°时,∠AEB=∠AEF;③当∠DAF=15°时,△AEF为等边三角形;④当CE=(2-)BC时,BE+DF=EF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共5小题,每小题3分,共15分)
11.在△ABC中,∠ABC=90°,∠A=28°,D是AC的中点,则∠CBD=________°.
12.一个平行四边形的一边长是3,两条对角线的长分别是4和2,则此平行四边形的面积为________.
13.如图,点P是矩形ABCD的对角线AC的延长线上一点,PD=AC,∠P=52°,则∠PDC=________.
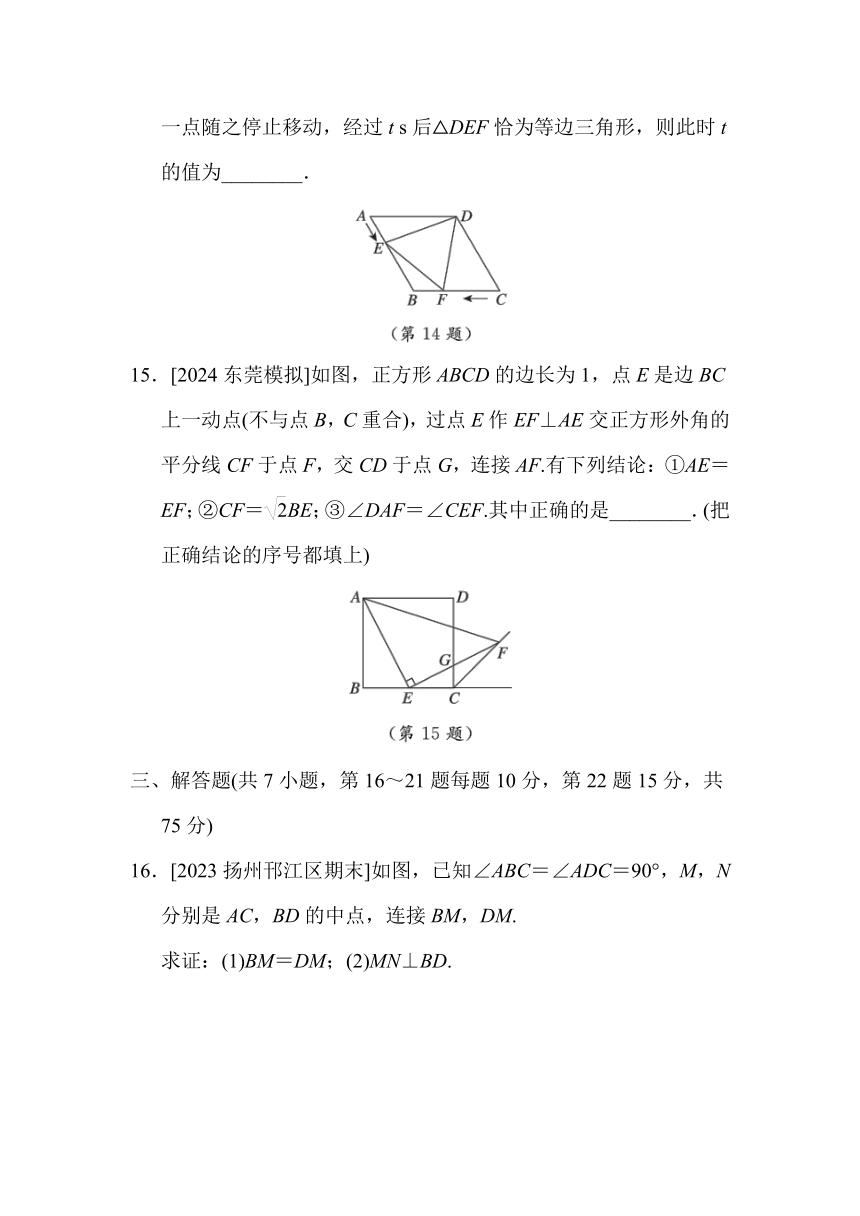
14. 如图,在菱形ABCD中,AB=10 cm,∠A=60°,点E,F同时从A,C两点出发,分别沿AB,CB方向向点B匀速移动,点E的速度为2 cm/s,点F的速度为4 cm/s,当一点到达B点时,另一点随之停止移动,经过t s后△DEF恰为等边三角形,则此时t的值为________.
15.[2024东莞模拟]如图,正方形ABCD的边长为1,点E是边BC上一动点(不与点B,C重合),过点E作EF⊥AE交正方形外角的平分线CF于点F,交CD于点G,连接AF.有下列结论:①AE=EF;②CF=BE;③∠DAF=∠CEF.其中正确的是________.(把正确结论的序号都填上)
三、解答题(共7小题,第16~21题每题10分,第22题15分,共75分)
16.[2023扬州邗江区期末]如图,已知∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,连接BM,DM.
求证:(1)BM=DM;(2)MN⊥BD.
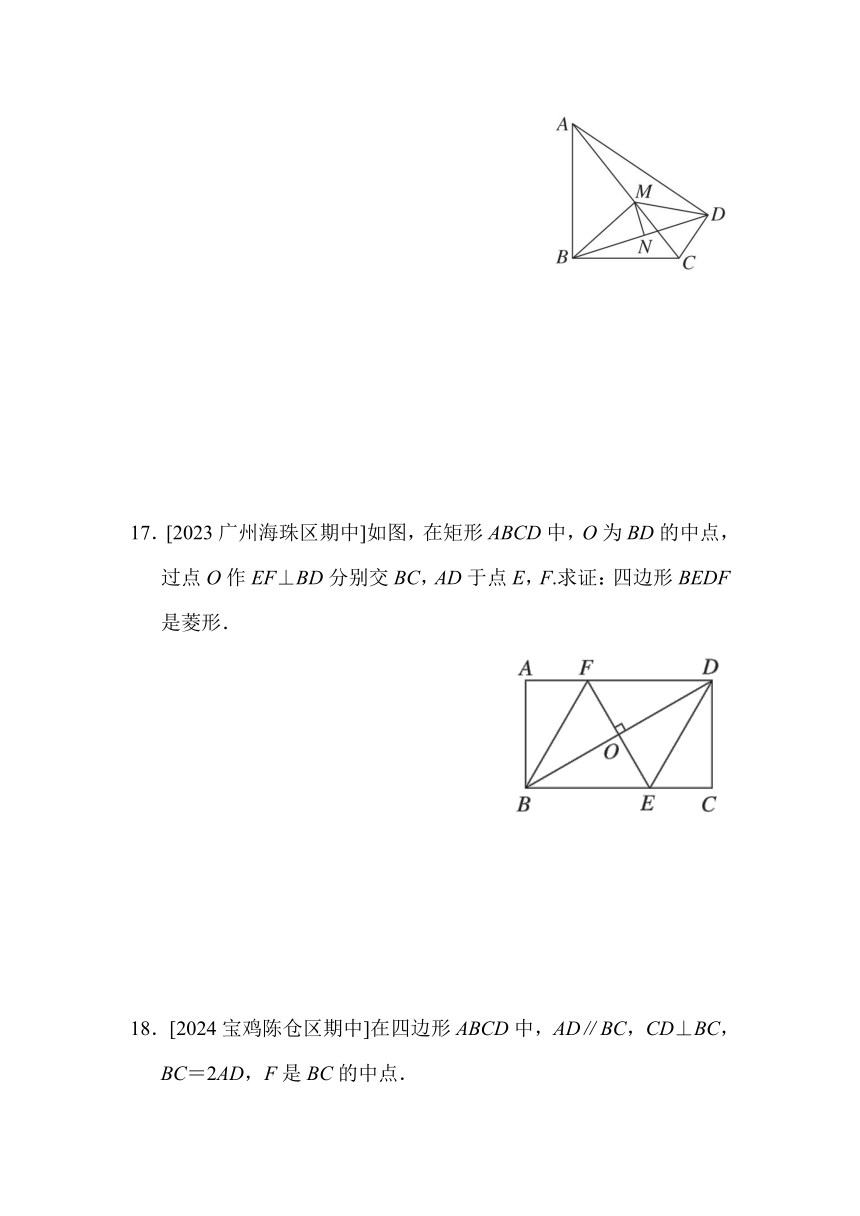
17.[2023广州海珠区期中]如图,在矩形ABCD中,O为BD的中点,过点O作EF⊥BD分别交BC,AD于点E,F.求证:四边形BEDF是菱形.
18.[2024宝鸡陈仓区期中]在四边形ABCD中,AD∥BC,CD⊥BC,BC=2AD,F是BC的中点.
(1)如图①,求证:四边形AFCD是矩形;
(2)如图②,过点C作CE⊥AB于点E,连接DE,EF.求证:DE=DC.
19.如图,在矩形ABCD中,点E在对角线AC上,点F在边CD上(点F与点C,D不重合),BE⊥EF,∠ABE+∠CEF=45°.
(1)求∠1+∠2的度数;
(2)求证:四边形ABCD是正方形.
20. 在正方形ABCD中,点G是边DC上的一点,点F是直线BC上一动点,FE⊥AG于H,交直线AD于点E.
(1)当点F运动到与点B重合时(如图①),线段EF与AG的数量关系是________.
(2)当点F运动到如图②所示的位置时,(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
21.如图,在矩形ABCD中,AB=6,BC=8,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为每秒1个单位长度,运动时间为t秒,其中0≤t≤10.
(1)若G,H分别是AD,BC的中点,则四边形EGFH一定是怎样的四边形(E,F相遇时除外)
答:________.(直接填空,不用说理)
(2)在(1)的条件下,若四边形EGFH为矩形,求t的值.
(3)在(1)的条件下,若G向D点运动,H向B点运动,且与点E,F以相同的速度同时出发,若四边形EGFH为菱形,求t的值.
22. 如图,四边形ABCD是正方形,点P在射线AC上,点E在射线BC上,且PB=PE,连接PD,点O为线段AC的中点.
【感知】如图①,当点P在线段AO上(点P不与点A,O重合)时,
①易证:△ABP≌△ADP(不需要证明).进而得到PE与PD的数量关系是__________;
②过点P作PM⊥CD于点M,PN⊥BC于点N,易证:Rt△PNE≌Rt△PMD(不需要证明).进而得到PE与PD的位置关系是__________;
【探究】如图②,当点P在线段OC上(点P不与点O,C重合)时,试写出PE与PD的数量关系和位置关系,并说明理由;
【应用】如图③,当点P在AC的延长线上时,直接写出当AB=3,CP=时线段DE的长.
INCLUDEPICTURE"章2.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章2.EPS" \* MERGEFORMATINET 答案
一、1.D 2.D 3.B 4.C 5.C 6.D 7.C 8.D
9.D 【点拨】∵点M,N分别是边AD,CD的中点,
∴MN是△ACD的中位线.
∴AC=2MN=2×3=6.
∵四边形ABCD是菱形,S菱形ABCD=24,
∴OA=OC=AC=3,OB=OD,AC⊥BD,
AC·BD=24.
即×6×BD=24,
∴BD=8.
∴OD=BD=4.
∴在Rt△OCD中,由勾股定理得CD===5.
∵点M是AD的中点,OA=OC,
∴OM是△ACD的中位线,
∴OM=CD=2.5.
10.D 【点拨】∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=∠BAD=∠BCD=90°,∠BAC=∠DAC=45°.
又∵AE=AF,∴Rt△ABE≌Rt△ADF.
∴BE=DF,∠BAE=∠DAF.
∴∠EAC=∠FAC.
∴AC垂直平分EF,故①正确;
∵∠EAF=45°,
∴易得∠EAC=∠FAC=∠BAE=∠DAF=22.5°.
∴∠BEA=90°-∠BAE=90°-22.5°=67.5°.
∵BC=CD,BE=DF,∴CE=CF.
∴∠CEF=45°.
∴∠AEF=180°-∠CEF-∠BEA=180°-45°-67.5°=67.5°=∠AEB,故②正确;
∵∠DAF=15°,
∴∠EAF=∠BAD-∠BAE-∠DAF=90°-15°-15°=60°.
∵AE=AF,
∴△AEF为等边三角形,故③正确;
∵CE=(2-)BC,
∴BE=DF=BC-CE=BC-(2-)BC=(-1)BC.
∴BE+DF=2(-1)BC.
∴EF==EC=(2-)BC=2(-1)BC=BE+DF,故④正确;
∴正确的结论有4个.
二、11.62 12.4 13.12° 14.
15.①② 【点拨】如图,在AB上取点H,使AH=EC,连接EH.
∵四边形ABCD是正方形,EF⊥AE,
∴∠BCD=∠B=∠AEF=90°,AB=BC.
∴∠HAE+∠AEB=90°,∠CEF+∠AEB=90°,
∴∠HAE=∠CEF.
∵AH=CE,AB=BC,
∴BH=BE.
∴△BHE为等腰直角三角形.
∴易得∠AHE=135°.
∵CF是正方形外角的平分线,
∴易得∠ECF=135°.∴∠AHE=∠ECF.
在△AHE和△ECF中,
∴△AHE≌△ECF(ASA).
∴AE=EF,EH=CF,∠AEH=∠EFC.故①正确;
∵BE=BH,∠B=90°,
∴EH==BE.
∴CF=BE.故②正确;
∵∠AHE=135°,
∴∠HAE+∠AEH=45°.
∵AE=EF,∠AEF=90°,
∴∠EAF=45°.
∴∠HAE+∠DAF=45°.
∴∠AEH=∠DAF.
∵∠AEH=∠EFC,
∴∠DAF=∠EFC.
而∠FEC不一定等于∠EFC,
∴∠DAF不一定等于∠FEC,故③错误.
故答案为①②.
三、16.【证明】(1)∵∠ABC=∠ADC=90°,M是AC的中点,
∴BM=AC,DM=AC.
∴BM=DM.
(2)∵点N是BD的中点,BM=DM,
∴MN⊥BD.
17.【证明】如图,
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠1=∠2.
∵O为BD的中点,
∴BO=DO.
∵∠BOE=∠DOF,
∴△OBE≌△ODF(ASA).
∴BE=DF.
∴四边形BEDF是平行四边形.
又∵EF⊥BD,
∴四边形BEDF是菱形.
18.【证明】(1)∵F是BC的中点,
∴BF=CF=BC.
∵BC=2AD,∴AD=BC.
∴AD=CF=BF.
∵AD∥BC,
∴四边形AFCD是平行四边形.
又∵CD⊥BC,∴∠DCF=90°.
∴四边形AFCD是矩形.
(2)如图,连接DF交CE于G,
由(1)知AD=BF.
∵AD∥BC,
∴四边形ABFD是平行四边形.
∴AB∥DF.
∵CE⊥AB,∴∠BEC=90°,CE⊥DF.
又∵F是BC的中点,
∴EF=BC=CF.
∴GE=GC.
∴DF是线段CE的垂直平分线.
∴DE=DC.
19.(1)【解】∵四边形ABCD为矩形,
∴∠ABC=90°.
∴∠ABE+∠1=90°.
∵BE⊥EF,
∴∠CEF+∠2=90°.
∵∠ABE+∠CEF=45°,
∴∠1+∠2=90°+90°-45°=135°.
(2)【证明】∵∠1+∠2+∠ACB=180°,
∴∠ACB=180°-(∠1+∠2)=180°-135°=45°.
∵∠ABC=90°,∴∠BAC+∠ACB=90°.
∴∠BAC=90°-∠ACB=90°-45°=45°.
∴∠ACB=∠BAC.
∴AB=BC.
∴四边形ABCD是正方形.
20.【解】(1)EF=AG 【点拨】∵四边形ABCD是正方形,
∴∠BAE=∠ADG=90°,AB=AD.
∴∠ABE+∠AEB=90°.
∵EF⊥AG,∴∠AHE=90°.
∴∠AEB+∠DAG=90°.
∴∠ABE=∠DAG.
∴△ABE≌△DAG(ASA).
∴EF=BE=AG.
(2)成立.证明:如图,过点F作FM⊥AE,垂足为M,则∠EMF=90°.
∵四边形ABCD是正方形,
∴∠ADG=90°,AD=CD.
∴易得MF=CD=AD.
∵EF⊥AH,∴∠AHE=90°,
∴∠HAE+∠E=90°.
又∵∠E+∠EFM=90°,
∴∠HAE=∠EFM.
∴△ADG≌△FME(ASA).
∴EF=AG.
21.【解】(1)四边形EGFH是平行四边形
(2)如图①,②,连接GH.
由题意易得AG=BH,AG∥BH,∠B=90°,
∴四边形ABHG是矩形.
∴GH=AB=6.
①如图①,当四边形EGFH是矩形时,EF=GH=6.
∵在Rt△ABC中,AB=6,BC=8,
∴AC=10.
∵AE=CF=t,∴EF=10-2t=6.
∴t=2.
②如图②,当四边形EGFH是矩形时,
∵EF=GH=6,AE=CF=t,
∴EF=t+t-10=2t-10=6.
∴t=8.
综上,当四边形EGFH为矩形时,t的值为2或8.
(3)如图③,M和N分别是AD和BC的中点,连接AH,CG,GH,AC与GH交于O.
∵四边形ABCD为矩形,
∴OA=OC,AD=BC=8.
∴AM=4.
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH.
∴ AG=AH.
∴四边形AGCH为菱形.
∴AG=CG.
设AG=CG=x,则DG=8-x,
∴在Rt△CDG中,由勾股定理可得CD2+DG2=CG2,
即62+(8-x)2=x2,解得x=.
∴MG=-4=,即t=,
∴当t的值为时,四边形EGFH为菱形.
22.【解】【感知】①PE=PD 【点拨】∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°.
在△ABP和△ADP中,
∴△ABP≌△ADP(SAS).
∴PB=PD.
∵PB=PE,
∴PE=PD.
②PE⊥PD 【点拨】由题意得∠PNE=∠PMD=∠PMC=90°.∵四边形ABCD是正方形,
∴CP平分∠MCN,∠NCM=90°.
∴四边形PMCN是矩形,PN=PM.
∴∠MPN=90°.
在Rt△PNE和Rt△PMD中,
∴Rt△PNE≌Rt△PMD(HL).
∴∠EPN=∠DPM.
∵∠MPN=∠MPE+∠EPN=90°,
∴∠MPE+∠DPM=90°,
即∠DPE=90°.
∴PE⊥PD.
【探究】PE与PD的数量关系和位置关系为PE=PD,
PE⊥PD,理由如下:
设PE交CD于F.
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,∠ACB=∠ACD=45°.
在△CBP和△CDP中,
∴△CBP≌△CDP(SAS).
∴PD=PB,∠PBC=∠PDF.
又∵PB=PE,
∴PD=PE,∠PBE=∠PEB.
∴∠PDF=∠PEB.
∵∠PFD=∠CFE,
∴180°-∠PFD-∠PDC=180°-∠CFE-∠PEB,
即∠DPF=∠ECF.
∵∠ECF=∠BCD=90°,
∴∠DPF=90°.
∴PD⊥PE.
【应用】线段DE的长为. 【点拨】设PD交BE于H.由题意易证△CBP≌△CDP.
∴PB=PD,∠PBC=∠PDC.
∴易得∠PDC=∠PEB,PE=PD.
∵∠PHE=∠CHD,
∴180°-∠CHD-∠PDC=180°-∠PHE-∠PEB,
即∠DPE=∠DCE.
又∵易知∠DCE=90°,
∴∠DPE=90°.
∴△DPE是等腰直角三角形.
过点P作PQ⊥BE于Q,
∵PB=PE,∴BQ=EQ.
∵∠PCQ=∠ACB=45°,
∴△CQP是等腰直角三角形.
∴CQ=PQ=CP=1.
∴EQ=BQ=BC+CQ=AB+CQ=3+1=4.
∴PE===.
∴DE==PE=×=.
一、选择题(共10小题,每小题3分,共30分)
1.[2023揭阳期末]菱形、矩形、正方形都具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.四条边相等,四个角相等 D.两组对边分别平行且相等
2.[2024邢台襄都区模拟]如图,在四边形ABCD中,给出部分数据,若添加一个数据后,四边形ABCD是矩形,则添加的数据是( )
A.CD=4 B.CD=2 C.OD=2 D.OD=4
3.[2023成都温江区期末]如图,F是正方形ABCD对角线BD上 一点,连接AF,CF,并延长CF交AD于点E.若∠AFC=130°,则∠DEC的度数为( )
A.65° B.70° C.75° D.80°
4.[2022安徽]两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α-90° B.α-45° C.180°-α D.270°-α
5.[2023东莞期中]若顺次连接某四边形四边中点所得的四边形是矩形,则原四边形一定是( )
A.菱形 B.矩形
C.对角线互相垂直的四边形 D.对角线相等的四边形
6. 三个边长为8 cm的正方形按如图所示的方式重叠在一起,点O是其中一个正方形的中心,则重叠部分(阴影)的面积为( )
A.16 cm2 B.24 cm2 C.28 cm2 D.32 cm2
7.在∠MON的两边上分别截取OA,OB,使OA=OB;分别以点A,B为圆心,OA长为半径作弧,两弧交于点C;连接AC,BC,AB,OC.若AB=2 cm,四边形OACB的面积为4 cm2.则OC的长为( )
A.2 cm B.3 cm C.4 cm D.5 cm
8. 如图,在矩形OABC中,点B的坐标是(5,12),则AC的长是( )
A.5 B.7 C.12 D.13
9.如图,在菱形ABCD中,对角线AC,BD相交于点O,点M,N分别是边AD,CD的中点,连接MN,OM,若MN=3,S菱形ABCD=24,则OM的长为( )
A.3 B.3.5 C.2 D.2.5
10.如图,在正方形ABCD中,点E,F分别在边BC,CD上, AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②当∠EAF=45°时,∠AEB=∠AEF;③当∠DAF=15°时,△AEF为等边三角形;④当CE=(2-)BC时,BE+DF=EF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共5小题,每小题3分,共15分)
11.在△ABC中,∠ABC=90°,∠A=28°,D是AC的中点,则∠CBD=________°.
12.一个平行四边形的一边长是3,两条对角线的长分别是4和2,则此平行四边形的面积为________.
13.如图,点P是矩形ABCD的对角线AC的延长线上一点,PD=AC,∠P=52°,则∠PDC=________.
14. 如图,在菱形ABCD中,AB=10 cm,∠A=60°,点E,F同时从A,C两点出发,分别沿AB,CB方向向点B匀速移动,点E的速度为2 cm/s,点F的速度为4 cm/s,当一点到达B点时,另一点随之停止移动,经过t s后△DEF恰为等边三角形,则此时t的值为________.
15.[2024东莞模拟]如图,正方形ABCD的边长为1,点E是边BC上一动点(不与点B,C重合),过点E作EF⊥AE交正方形外角的平分线CF于点F,交CD于点G,连接AF.有下列结论:①AE=EF;②CF=BE;③∠DAF=∠CEF.其中正确的是________.(把正确结论的序号都填上)
三、解答题(共7小题,第16~21题每题10分,第22题15分,共75分)
16.[2023扬州邗江区期末]如图,已知∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,连接BM,DM.
求证:(1)BM=DM;(2)MN⊥BD.
17.[2023广州海珠区期中]如图,在矩形ABCD中,O为BD的中点,过点O作EF⊥BD分别交BC,AD于点E,F.求证:四边形BEDF是菱形.
18.[2024宝鸡陈仓区期中]在四边形ABCD中,AD∥BC,CD⊥BC,BC=2AD,F是BC的中点.
(1)如图①,求证:四边形AFCD是矩形;
(2)如图②,过点C作CE⊥AB于点E,连接DE,EF.求证:DE=DC.
19.如图,在矩形ABCD中,点E在对角线AC上,点F在边CD上(点F与点C,D不重合),BE⊥EF,∠ABE+∠CEF=45°.
(1)求∠1+∠2的度数;
(2)求证:四边形ABCD是正方形.
20. 在正方形ABCD中,点G是边DC上的一点,点F是直线BC上一动点,FE⊥AG于H,交直线AD于点E.
(1)当点F运动到与点B重合时(如图①),线段EF与AG的数量关系是________.
(2)当点F运动到如图②所示的位置时,(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
21.如图,在矩形ABCD中,AB=6,BC=8,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为每秒1个单位长度,运动时间为t秒,其中0≤t≤10.
(1)若G,H分别是AD,BC的中点,则四边形EGFH一定是怎样的四边形(E,F相遇时除外)
答:________.(直接填空,不用说理)
(2)在(1)的条件下,若四边形EGFH为矩形,求t的值.
(3)在(1)的条件下,若G向D点运动,H向B点运动,且与点E,F以相同的速度同时出发,若四边形EGFH为菱形,求t的值.
22. 如图,四边形ABCD是正方形,点P在射线AC上,点E在射线BC上,且PB=PE,连接PD,点O为线段AC的中点.
【感知】如图①,当点P在线段AO上(点P不与点A,O重合)时,
①易证:△ABP≌△ADP(不需要证明).进而得到PE与PD的数量关系是__________;
②过点P作PM⊥CD于点M,PN⊥BC于点N,易证:Rt△PNE≌Rt△PMD(不需要证明).进而得到PE与PD的位置关系是__________;
【探究】如图②,当点P在线段OC上(点P不与点O,C重合)时,试写出PE与PD的数量关系和位置关系,并说明理由;
【应用】如图③,当点P在AC的延长线上时,直接写出当AB=3,CP=时线段DE的长.
INCLUDEPICTURE"章2.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 BS\\章2.EPS" \* MERGEFORMATINET 答案
一、1.D 2.D 3.B 4.C 5.C 6.D 7.C 8.D
9.D 【点拨】∵点M,N分别是边AD,CD的中点,
∴MN是△ACD的中位线.
∴AC=2MN=2×3=6.
∵四边形ABCD是菱形,S菱形ABCD=24,
∴OA=OC=AC=3,OB=OD,AC⊥BD,
AC·BD=24.
即×6×BD=24,
∴BD=8.
∴OD=BD=4.
∴在Rt△OCD中,由勾股定理得CD===5.
∵点M是AD的中点,OA=OC,
∴OM是△ACD的中位线,
∴OM=CD=2.5.
10.D 【点拨】∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=∠BAD=∠BCD=90°,∠BAC=∠DAC=45°.
又∵AE=AF,∴Rt△ABE≌Rt△ADF.
∴BE=DF,∠BAE=∠DAF.
∴∠EAC=∠FAC.
∴AC垂直平分EF,故①正确;
∵∠EAF=45°,
∴易得∠EAC=∠FAC=∠BAE=∠DAF=22.5°.
∴∠BEA=90°-∠BAE=90°-22.5°=67.5°.
∵BC=CD,BE=DF,∴CE=CF.
∴∠CEF=45°.
∴∠AEF=180°-∠CEF-∠BEA=180°-45°-67.5°=67.5°=∠AEB,故②正确;
∵∠DAF=15°,
∴∠EAF=∠BAD-∠BAE-∠DAF=90°-15°-15°=60°.
∵AE=AF,
∴△AEF为等边三角形,故③正确;
∵CE=(2-)BC,
∴BE=DF=BC-CE=BC-(2-)BC=(-1)BC.
∴BE+DF=2(-1)BC.
∴EF==EC=(2-)BC=2(-1)BC=BE+DF,故④正确;
∴正确的结论有4个.
二、11.62 12.4 13.12° 14.
15.①② 【点拨】如图,在AB上取点H,使AH=EC,连接EH.
∵四边形ABCD是正方形,EF⊥AE,
∴∠BCD=∠B=∠AEF=90°,AB=BC.
∴∠HAE+∠AEB=90°,∠CEF+∠AEB=90°,
∴∠HAE=∠CEF.
∵AH=CE,AB=BC,
∴BH=BE.
∴△BHE为等腰直角三角形.
∴易得∠AHE=135°.
∵CF是正方形外角的平分线,
∴易得∠ECF=135°.∴∠AHE=∠ECF.
在△AHE和△ECF中,
∴△AHE≌△ECF(ASA).
∴AE=EF,EH=CF,∠AEH=∠EFC.故①正确;
∵BE=BH,∠B=90°,
∴EH==BE.
∴CF=BE.故②正确;
∵∠AHE=135°,
∴∠HAE+∠AEH=45°.
∵AE=EF,∠AEF=90°,
∴∠EAF=45°.
∴∠HAE+∠DAF=45°.
∴∠AEH=∠DAF.
∵∠AEH=∠EFC,
∴∠DAF=∠EFC.
而∠FEC不一定等于∠EFC,
∴∠DAF不一定等于∠FEC,故③错误.
故答案为①②.
三、16.【证明】(1)∵∠ABC=∠ADC=90°,M是AC的中点,
∴BM=AC,DM=AC.
∴BM=DM.
(2)∵点N是BD的中点,BM=DM,
∴MN⊥BD.
17.【证明】如图,
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠1=∠2.
∵O为BD的中点,
∴BO=DO.
∵∠BOE=∠DOF,
∴△OBE≌△ODF(ASA).
∴BE=DF.
∴四边形BEDF是平行四边形.
又∵EF⊥BD,
∴四边形BEDF是菱形.
18.【证明】(1)∵F是BC的中点,
∴BF=CF=BC.
∵BC=2AD,∴AD=BC.
∴AD=CF=BF.
∵AD∥BC,
∴四边形AFCD是平行四边形.
又∵CD⊥BC,∴∠DCF=90°.
∴四边形AFCD是矩形.
(2)如图,连接DF交CE于G,
由(1)知AD=BF.
∵AD∥BC,
∴四边形ABFD是平行四边形.
∴AB∥DF.
∵CE⊥AB,∴∠BEC=90°,CE⊥DF.
又∵F是BC的中点,
∴EF=BC=CF.
∴GE=GC.
∴DF是线段CE的垂直平分线.
∴DE=DC.
19.(1)【解】∵四边形ABCD为矩形,
∴∠ABC=90°.
∴∠ABE+∠1=90°.
∵BE⊥EF,
∴∠CEF+∠2=90°.
∵∠ABE+∠CEF=45°,
∴∠1+∠2=90°+90°-45°=135°.
(2)【证明】∵∠1+∠2+∠ACB=180°,
∴∠ACB=180°-(∠1+∠2)=180°-135°=45°.
∵∠ABC=90°,∴∠BAC+∠ACB=90°.
∴∠BAC=90°-∠ACB=90°-45°=45°.
∴∠ACB=∠BAC.
∴AB=BC.
∴四边形ABCD是正方形.
20.【解】(1)EF=AG 【点拨】∵四边形ABCD是正方形,
∴∠BAE=∠ADG=90°,AB=AD.
∴∠ABE+∠AEB=90°.
∵EF⊥AG,∴∠AHE=90°.
∴∠AEB+∠DAG=90°.
∴∠ABE=∠DAG.
∴△ABE≌△DAG(ASA).
∴EF=BE=AG.
(2)成立.证明:如图,过点F作FM⊥AE,垂足为M,则∠EMF=90°.
∵四边形ABCD是正方形,
∴∠ADG=90°,AD=CD.
∴易得MF=CD=AD.
∵EF⊥AH,∴∠AHE=90°,
∴∠HAE+∠E=90°.
又∵∠E+∠EFM=90°,
∴∠HAE=∠EFM.
∴△ADG≌△FME(ASA).
∴EF=AG.
21.【解】(1)四边形EGFH是平行四边形
(2)如图①,②,连接GH.
由题意易得AG=BH,AG∥BH,∠B=90°,
∴四边形ABHG是矩形.
∴GH=AB=6.
①如图①,当四边形EGFH是矩形时,EF=GH=6.
∵在Rt△ABC中,AB=6,BC=8,
∴AC=10.
∵AE=CF=t,∴EF=10-2t=6.
∴t=2.
②如图②,当四边形EGFH是矩形时,
∵EF=GH=6,AE=CF=t,
∴EF=t+t-10=2t-10=6.
∴t=8.
综上,当四边形EGFH为矩形时,t的值为2或8.
(3)如图③,M和N分别是AD和BC的中点,连接AH,CG,GH,AC与GH交于O.
∵四边形ABCD为矩形,
∴OA=OC,AD=BC=8.
∴AM=4.
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH.
∴ AG=AH.
∴四边形AGCH为菱形.
∴AG=CG.
设AG=CG=x,则DG=8-x,
∴在Rt△CDG中,由勾股定理可得CD2+DG2=CG2,
即62+(8-x)2=x2,解得x=.
∴MG=-4=,即t=,
∴当t的值为时,四边形EGFH为菱形.
22.【解】【感知】①PE=PD 【点拨】∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°.
在△ABP和△ADP中,
∴△ABP≌△ADP(SAS).
∴PB=PD.
∵PB=PE,
∴PE=PD.
②PE⊥PD 【点拨】由题意得∠PNE=∠PMD=∠PMC=90°.∵四边形ABCD是正方形,
∴CP平分∠MCN,∠NCM=90°.
∴四边形PMCN是矩形,PN=PM.
∴∠MPN=90°.
在Rt△PNE和Rt△PMD中,
∴Rt△PNE≌Rt△PMD(HL).
∴∠EPN=∠DPM.
∵∠MPN=∠MPE+∠EPN=90°,
∴∠MPE+∠DPM=90°,
即∠DPE=90°.
∴PE⊥PD.
【探究】PE与PD的数量关系和位置关系为PE=PD,
PE⊥PD,理由如下:
设PE交CD于F.
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,∠ACB=∠ACD=45°.
在△CBP和△CDP中,
∴△CBP≌△CDP(SAS).
∴PD=PB,∠PBC=∠PDF.
又∵PB=PE,
∴PD=PE,∠PBE=∠PEB.
∴∠PDF=∠PEB.
∵∠PFD=∠CFE,
∴180°-∠PFD-∠PDC=180°-∠CFE-∠PEB,
即∠DPF=∠ECF.
∵∠ECF=∠BCD=90°,
∴∠DPF=90°.
∴PD⊥PE.
【应用】线段DE的长为. 【点拨】设PD交BE于H.由题意易证△CBP≌△CDP.
∴PB=PD,∠PBC=∠PDC.
∴易得∠PDC=∠PEB,PE=PD.
∵∠PHE=∠CHD,
∴180°-∠CHD-∠PDC=180°-∠PHE-∠PEB,
即∠DPE=∠DCE.
又∵易知∠DCE=90°,
∴∠DPE=90°.
∴△DPE是等腰直角三角形.
过点P作PQ⊥BE于Q,
∵PB=PE,∴BQ=EQ.
∵∠PCQ=∠ACB=45°,
∴△CQP是等腰直角三角形.
∴CQ=PQ=CP=1.
∴EQ=BQ=BC+CQ=AB+CQ=3+1=4.
∴PE===.
∴DE==PE=×=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
