广东省梅州东山中学08-09学年高二下学期期末考试(数学文)
文档属性
| 名称 | 广东省梅州东山中学08-09学年高二下学期期末考试(数学文) |

|
|
| 格式 | rar | ||
| 文件大小 | 217.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览


文档简介
梅县东山中学高二数学(文)期末考试题(2009.7)
出题人 范立东 李志辉 审题人 王奇芬
一、选择题:(每小题5分,共50分)
1.设集合,则( )
(A). (B).
(C). (D).
2.“”是“”的( )w.w.w.k.s.5.u.c.o.m
(A).充分而不必要条件 (B).必要而不充分条件
(C).充分必要条件 (D).既不充分也不必要条件
3.命题“存在R,0”的否定是w.w.w.k.s.5.u.c.o.m
(A)不存在R, >0 (B)存在R, 0
(C)对任意的R, 0 (D)对任意的R, >0
4.已知的值是( )
(A).10 (B). (C). (D).0
5.函数的值域为( )
(A). (B). (C). (D).
6.已知函数是上的偶函数,若对于,都有,且当时,,则的值为( )
(A). ( B). (C). (D).
7.关于x的方程的两根为且则b的取值范围( )
(A).b>-2 (B).b<-2 (C).b<-2或b>2 (D).b<2
8.函数的增区间是( )
(A). (B). (C). (D).
9.已知偶函数在区间单调递增,则满足<的x 取值范围是
(A).(,) (B). [,) (C). (,) (D). [,)
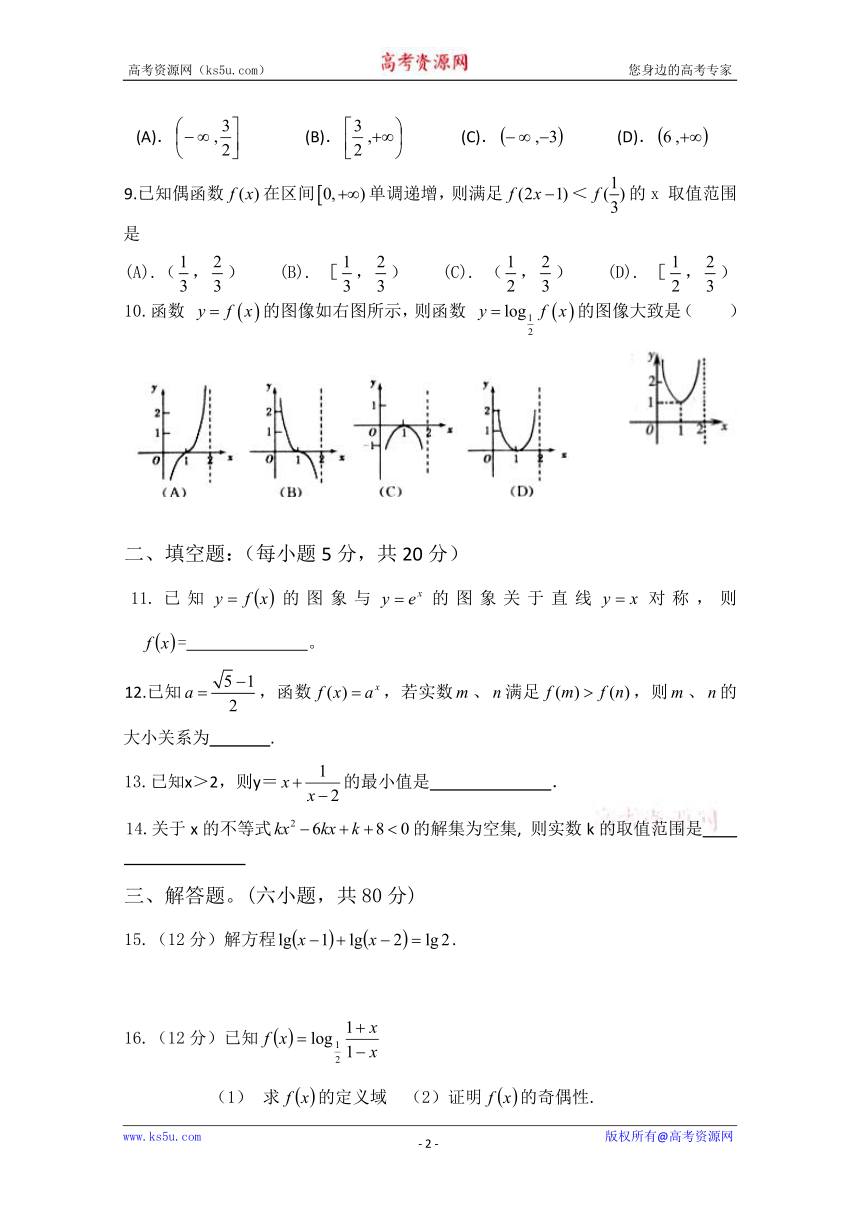
10.函数 的图像如右图所示,则函数 的图像大致是( )
二、填空题:(每小题5分,共20分)
11.已知的图象与的图象关于直线对称,则= 。
12.已知,函数,若实数、满足,则、的大小关系为 .
13.已知x>2,则y=的最小值是 .
14.关于x的不等式的解集为空集, 则实数k的取值范围是
三、解答题。(六小题,共80分)
15.(12分)解方程.
16.(12分)已知
求的定义域 (2)证明的奇偶性.
17.(14分)设有两个命题,p:关于x的不等式(a>0,且a≠1)的解集是{x|x<0};q:函数的定义域为R。如果为真命题,为假命题,求实数a的取值范围.
18.(14分)设的定义域为,且在上为增函数,。
(1)求证.
(2)设解不等式.
19.(14分)已知二次函数的定义域为R,处取得最值。若为一次函数,且.
(1)求的解析式。
(2)若恒成立,求t的取值范围.
20.(14分)已知函数().
(I)若的定义域和值域均是,求实数的值;
(II)若在区间上是减函数,且对任意的,,总有,求实数的取值范围.
广东梅县东山中学高二文科数学期末考试答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
B
B
C
B
C
A
C
二、填空题
11.;12.;13.4;14.
三、解答题
15.解:原方程
∴原方程的解为:
16.解:(1)由 ∴定义域为
证明(2)∵由(1)可知定义域关于原点对称
且 ∴为奇函数
17.解:p为真,则有:
q为真,恒成立
由为真命题,为假命题可得:、一真一假
(1)若p真q假,则有
(2)若p假q真,则有
综上所得:
18.(1)证明:令,则有
∵定义域为(0,+)
∴
(2)解:∵ ∴
又∵在(0,+)上为增函数 ∴原不等式
∴原不等式解集为
19.(1)解,依题意设
∵ ∴ ∴
∴
(2)解:由(1)可知的对称轴为
当时,在上为增函数 ∴
由得 ∴
当时,在[-1,2]上的最小值为
由得 ∴
当时在[-1,2]上为减函数 ∴
由得 ∴
综上所述:
20.解:∵(1)
∴在上为减函数,又定义域和值域均有
∴
(2)∵在上为减函数 ∴
又∵对称轴且
∴在上的最大、最小值分别为,
又∵对总有
又∵ ∴
∴
本试卷由21世纪教育网http://www.21cnjy.com/供稿,下载更多教学资源,请登录21世纪教育网
w.w.w.k.s.5.u.c.o.m
出题人 范立东 李志辉 审题人 王奇芬
一、选择题:(每小题5分,共50分)
1.设集合,则( )
(A). (B).
(C). (D).
2.“”是“”的( )w.w.w.k.s.5.u.c.o.m
(A).充分而不必要条件 (B).必要而不充分条件
(C).充分必要条件 (D).既不充分也不必要条件
3.命题“存在R,0”的否定是w.w.w.k.s.5.u.c.o.m
(A)不存在R, >0 (B)存在R, 0
(C)对任意的R, 0 (D)对任意的R, >0
4.已知的值是( )
(A).10 (B). (C). (D).0
5.函数的值域为( )
(A). (B). (C). (D).
6.已知函数是上的偶函数,若对于,都有,且当时,,则的值为( )
(A). ( B). (C). (D).
7.关于x的方程的两根为且则b的取值范围( )
(A).b>-2 (B).b<-2 (C).b<-2或b>2 (D).b<2
8.函数的增区间是( )
(A). (B). (C). (D).
9.已知偶函数在区间单调递增,则满足<的x 取值范围是
(A).(,) (B). [,) (C). (,) (D). [,)
10.函数 的图像如右图所示,则函数 的图像大致是( )
二、填空题:(每小题5分,共20分)
11.已知的图象与的图象关于直线对称,则= 。
12.已知,函数,若实数、满足,则、的大小关系为 .
13.已知x>2,则y=的最小值是 .
14.关于x的不等式的解集为空集, 则实数k的取值范围是
三、解答题。(六小题,共80分)
15.(12分)解方程.
16.(12分)已知
求的定义域 (2)证明的奇偶性.
17.(14分)设有两个命题,p:关于x的不等式(a>0,且a≠1)的解集是{x|x<0};q:函数的定义域为R。如果为真命题,为假命题,求实数a的取值范围.
18.(14分)设的定义域为,且在上为增函数,。
(1)求证.
(2)设解不等式.
19.(14分)已知二次函数的定义域为R,处取得最值。若为一次函数,且.
(1)求的解析式。
(2)若恒成立,求t的取值范围.
20.(14分)已知函数().
(I)若的定义域和值域均是,求实数的值;
(II)若在区间上是减函数,且对任意的,,总有,求实数的取值范围.
广东梅县东山中学高二文科数学期末考试答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
B
B
C
B
C
A
C
二、填空题
11.;12.;13.4;14.
三、解答题
15.解:原方程
∴原方程的解为:
16.解:(1)由 ∴定义域为
证明(2)∵由(1)可知定义域关于原点对称
且 ∴为奇函数
17.解:p为真,则有:
q为真,恒成立
由为真命题,为假命题可得:、一真一假
(1)若p真q假,则有
(2)若p假q真,则有
综上所得:
18.(1)证明:令,则有
∵定义域为(0,+)
∴
(2)解:∵ ∴
又∵在(0,+)上为增函数 ∴原不等式
∴原不等式解集为
19.(1)解,依题意设
∵ ∴ ∴
∴
(2)解:由(1)可知的对称轴为
当时,在上为增函数 ∴
由得 ∴
当时,在[-1,2]上的最小值为
由得 ∴
当时在[-1,2]上为减函数 ∴
由得 ∴
综上所述:
20.解:∵(1)
∴在上为减函数,又定义域和值域均有
∴
(2)∵在上为减函数 ∴
又∵对称轴且
∴在上的最大、最小值分别为,
又∵对总有
又∵ ∴
∴
本试卷由21世纪教育网http://www.21cnjy.com/供稿,下载更多教学资源,请登录21世纪教育网
w.w.w.k.s.5.u.c.o.m
同课章节目录
