安徽省阜阳市颍州区鸿升初级中学2023-2024学年八年级下学期期中数学试题(含答案)
文档属性
| 名称 | 安徽省阜阳市颍州区鸿升初级中学2023-2024学年八年级下学期期中数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-12 00:00:00 | ||
图片预览




文档简介
2023—2024学年度第二学期阜阳市鸿升中学期中检测卷
八年级数学
(满分:150分 考试时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.已知代数式在实数范围内有意义,则x的取值范围是( )
A. B. C.且 D.且
2.下列计算正确的是( )
A. B. C. D.
3.如图,DE是的中位线,若,则DE的长是( )
A.3 B.4 C.5 D.6
4.在中,,,的对边分别为a,b,c,下列条件中,不能判断是直角三角形的是( )
A., B.,,
C. D.,,
5.在下列定理中,逆命题错误的是( )
A.直角三角形斜边上的中线等于斜边的一半
B.等腰三角形的底角相等
C.线段的垂直平分线上的点到这条线段的两个端点距离相等
D.全等三角形的面积相等
6.如图,在中,,中线AF与中位线DE相交于点O,则四边形ADFE是( )
A.矩形 B.平行四边形 C.菱形 D.正方形
7.如图,在菱形ABCD中,,对角线AC,BD相交于点O,以OA,OD为边作矩形OAED,已知菱形的面积为,则( )
A.1 B.2 C. D.
8.如图,的对角线AC,BD相交于点O,过点O作于点F,延长FO交AD于点E,,,则的面积为( )
A.18 B.24 C.32 D.42
9.如图,延长矩形ABCD的边CB至点E,使,连接DE.若,则的度数是( )
A. B. C. D.
10.如图,正方形ABCO和正方形DEFO的顶点A,O,E在同一直线l上,且,,给出下列结论:①;②;③;④的面积是.其中正确的结论为( )
A.①③ B.①④ C.②③ D.①③④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知最简二次根式与二次根式是同类二次根式,则_________.
12.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别足4,6,2,4,则正方形E的边长是_________.
13.如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,分别以点C,E为圆心、大于的长为半径作弧,两弧交于点P,作射线BP交AD的延长线于点F.若,,则EF的长为_________.
14.新情境日常生活如图1,表示一双开门关闭时的状态图,如图2表示打开双门过程中,某一时刻的示意图,其中AB为门槛宽度.
(1)当时,双门间隙CD与门槛宽度AB的比值为_________;
(2)若双门间隙CD的距离为2寸,点C和点D距离AB都为1尺(1尺=10寸),则门槛宽度AB是_________寸.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(1); (2).
16.先化简,再求值:已知,求的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,正方形网格中的每个小正方形边长都为1.
(1)分别求出线段AB,AC,BC的长;
(2)判断的形状,并说明你的理由.
18.阅读材料:如果一个三角形的三边长分别为a,b,c,记,那么这个三角形的面积为.这个公式叫“海伦公式”,它是利用三角形的三条边的边长直接求三角形面积的公式,中国秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦—秦九韶公式”.完成下列问题:
如图,在中,,,.
(1)求的面积;
(2)过点A作,垂足为D,求线段AD的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平行四边形ABCD中,,,的平分线分别与BC,AD相交于点E,F.
(1)求证:;
(2)当AB与BC满足什么数量关系时,四边形AECF为菱形?请说明理由.
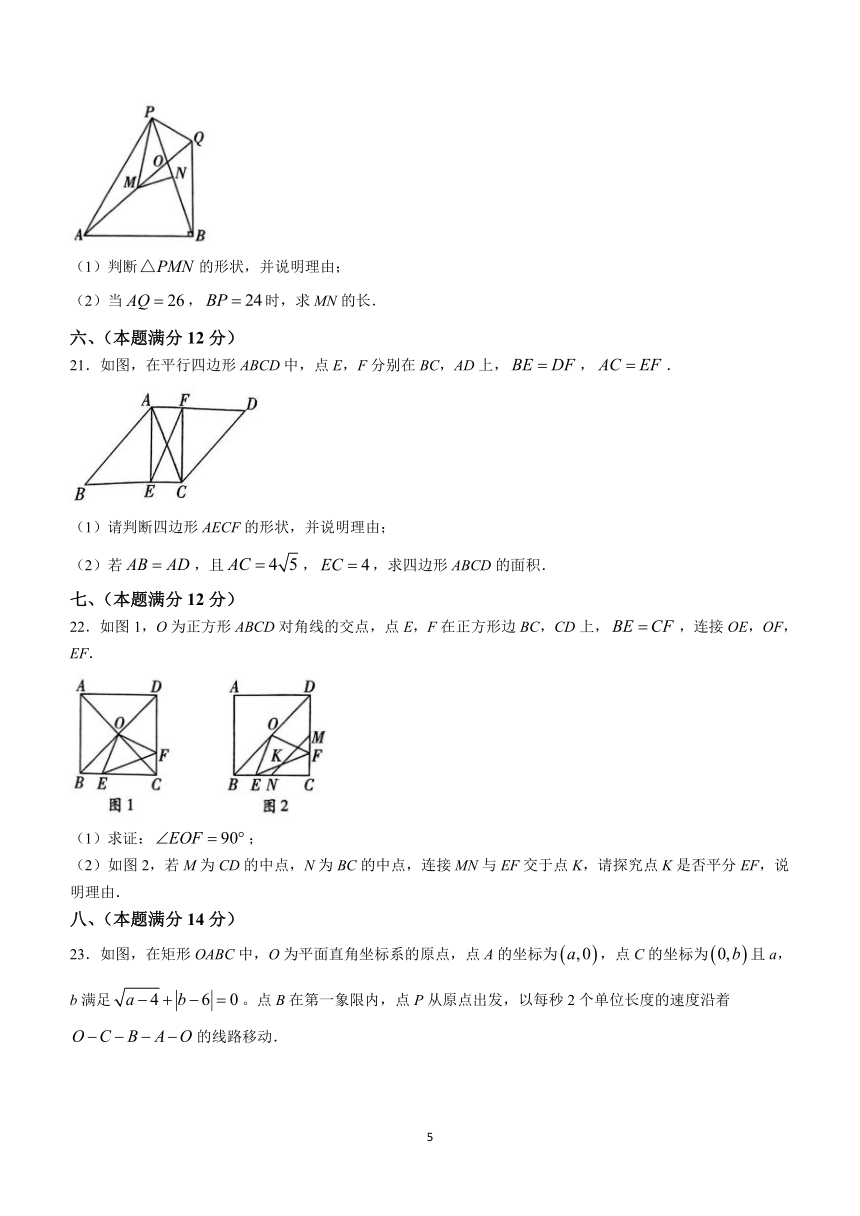
20.如图,在线段AB的同侧作和,PB和QA相交于点O,M,N分别是边AQ,BP的中点,连接PQ,PM,MN,.
(1)判断的形状,并说明理由;
(2)当,时,求MN的长.
六、(本题满分12分)
21.如图,在平行四边形ABCD中,点E,F分别在BC,AD上,,.
(1)请判断四边形AECF的形状,并说明理由;
(2)若,且,,求四边形ABCD的面积.
七、(本题满分12分)
22.如图1,O为正方形ABCD对角线的交点,点E,F在正方形边BC,CD上,,连接OE,OF,EF.
(1)求证:;
(2)如图2,若M为CD的中点,N为BC的中点,连接MN与EF交于点K,请探究点K是否平分EF,说明理由.
八、(本题满分14分)
23.如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为,点C的坐标为且a,b满足。点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着的线路移动.
(1)点B的坐标为_________;当点P移动3.5秒时,点P的坐标为_________;
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(3)在移动过程中,当的面积是10时,求点P移动的时间.
数学 八年级下册 参考答案
1.D 2.C 3.B 4.A 5.D 6.A 7.C 8.D 9.B 10.B
11.3 12.4 13.6 14.(1);(2)101
15.解:(1)原式;
(2)原式:.
16.解:,
,
则原式.
17.解:(1),,;
(2)是等腰三角形.
理由如下:
,,,
是等腰三角形.
18.解:(1),,,;
;
(2),,
19.(1)证明:四边形是平行四边形,
,,.
,,.
平分,平分,
,,
,
;
(2)解:当时,四边形为菱形.
理由:由题意,可知,
由(1)可知,,
和都是等边三角形,
,,,
四边形为平行四边形
又,是的中点,
,,四边形是菱形.
20.解:(1)为直角三角形,理由如下:如解图,连接.
,是的中点,
,,
.
又为的中点,,为直角三角形;
(2)由(1)知.
,.
又为的中点,且,.
,,.
又,.
21.解:(1)四边形是矩形.理由如下:
四边形是平行四边形,,
,即.,
四边形是平行四边形.
,四边形是矩形;
(2)由(1)知,,四边形是矩形,
.
,,.,
四边形为菱形,.
设,.
在直角三角形中,,即,
,,
四边形.
22.(1)证明:为正方形对角线的交点,
,,.
同理可得.
在和中,,
,,
,.
,
(2)解:点平分.理由如下:
如解图,过点作交的延长线于点,
为的中点,为的中点,
是的中位线,
,,,
.,,
,.
,,
,.
在和中,,
,即点平分.
23.解:(1),;
(2)由题意,得在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况,
第一种情况,当点P在OC上时,点P移动的时间是:;
第二种情况,当点P在BA上时,点P移动的时间是:.
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6s;
(3)设点P移动的时间为.如解图1所示,
的面积是10,,即,
解得,此时;
如解图2所示,
的面积是10,,即,
解得,,此时;
如解图3所示,
的面积是10,,即,
解得,此时;
如解图4所示,
的面积是10,,即,
解得,此时.
综上所述,满足条件的时间的值为或或或.
八年级数学
(满分:150分 考试时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.已知代数式在实数范围内有意义,则x的取值范围是( )
A. B. C.且 D.且
2.下列计算正确的是( )
A. B. C. D.
3.如图,DE是的中位线,若,则DE的长是( )
A.3 B.4 C.5 D.6
4.在中,,,的对边分别为a,b,c,下列条件中,不能判断是直角三角形的是( )
A., B.,,
C. D.,,
5.在下列定理中,逆命题错误的是( )
A.直角三角形斜边上的中线等于斜边的一半
B.等腰三角形的底角相等
C.线段的垂直平分线上的点到这条线段的两个端点距离相等
D.全等三角形的面积相等
6.如图,在中,,中线AF与中位线DE相交于点O,则四边形ADFE是( )
A.矩形 B.平行四边形 C.菱形 D.正方形
7.如图,在菱形ABCD中,,对角线AC,BD相交于点O,以OA,OD为边作矩形OAED,已知菱形的面积为,则( )
A.1 B.2 C. D.
8.如图,的对角线AC,BD相交于点O,过点O作于点F,延长FO交AD于点E,,,则的面积为( )
A.18 B.24 C.32 D.42
9.如图,延长矩形ABCD的边CB至点E,使,连接DE.若,则的度数是( )
A. B. C. D.
10.如图,正方形ABCO和正方形DEFO的顶点A,O,E在同一直线l上,且,,给出下列结论:①;②;③;④的面积是.其中正确的结论为( )
A.①③ B.①④ C.②③ D.①③④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知最简二次根式与二次根式是同类二次根式,则_________.
12.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别足4,6,2,4,则正方形E的边长是_________.
13.如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,分别以点C,E为圆心、大于的长为半径作弧,两弧交于点P,作射线BP交AD的延长线于点F.若,,则EF的长为_________.
14.新情境日常生活如图1,表示一双开门关闭时的状态图,如图2表示打开双门过程中,某一时刻的示意图,其中AB为门槛宽度.
(1)当时,双门间隙CD与门槛宽度AB的比值为_________;
(2)若双门间隙CD的距离为2寸,点C和点D距离AB都为1尺(1尺=10寸),则门槛宽度AB是_________寸.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(1); (2).
16.先化简,再求值:已知,求的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,正方形网格中的每个小正方形边长都为1.
(1)分别求出线段AB,AC,BC的长;
(2)判断的形状,并说明你的理由.
18.阅读材料:如果一个三角形的三边长分别为a,b,c,记,那么这个三角形的面积为.这个公式叫“海伦公式”,它是利用三角形的三条边的边长直接求三角形面积的公式,中国秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦—秦九韶公式”.完成下列问题:
如图,在中,,,.
(1)求的面积;
(2)过点A作,垂足为D,求线段AD的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平行四边形ABCD中,,,的平分线分别与BC,AD相交于点E,F.
(1)求证:;
(2)当AB与BC满足什么数量关系时,四边形AECF为菱形?请说明理由.
20.如图,在线段AB的同侧作和,PB和QA相交于点O,M,N分别是边AQ,BP的中点,连接PQ,PM,MN,.
(1)判断的形状,并说明理由;
(2)当,时,求MN的长.
六、(本题满分12分)
21.如图,在平行四边形ABCD中,点E,F分别在BC,AD上,,.
(1)请判断四边形AECF的形状,并说明理由;
(2)若,且,,求四边形ABCD的面积.
七、(本题满分12分)
22.如图1,O为正方形ABCD对角线的交点,点E,F在正方形边BC,CD上,,连接OE,OF,EF.
(1)求证:;
(2)如图2,若M为CD的中点,N为BC的中点,连接MN与EF交于点K,请探究点K是否平分EF,说明理由.
八、(本题满分14分)
23.如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为,点C的坐标为且a,b满足。点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着的线路移动.
(1)点B的坐标为_________;当点P移动3.5秒时,点P的坐标为_________;
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(3)在移动过程中,当的面积是10时,求点P移动的时间.
数学 八年级下册 参考答案
1.D 2.C 3.B 4.A 5.D 6.A 7.C 8.D 9.B 10.B
11.3 12.4 13.6 14.(1);(2)101
15.解:(1)原式;
(2)原式:.
16.解:,
,
则原式.
17.解:(1),,;
(2)是等腰三角形.
理由如下:
,,,
是等腰三角形.
18.解:(1),,,;
;
(2),,
19.(1)证明:四边形是平行四边形,
,,.
,,.
平分,平分,
,,
,
;
(2)解:当时,四边形为菱形.
理由:由题意,可知,
由(1)可知,,
和都是等边三角形,
,,,
四边形为平行四边形
又,是的中点,
,,四边形是菱形.
20.解:(1)为直角三角形,理由如下:如解图,连接.
,是的中点,
,,
.
又为的中点,,为直角三角形;
(2)由(1)知.
,.
又为的中点,且,.
,,.
又,.
21.解:(1)四边形是矩形.理由如下:
四边形是平行四边形,,
,即.,
四边形是平行四边形.
,四边形是矩形;
(2)由(1)知,,四边形是矩形,
.
,,.,
四边形为菱形,.
设,.
在直角三角形中,,即,
,,
四边形.
22.(1)证明:为正方形对角线的交点,
,,.
同理可得.
在和中,,
,,
,.
,
(2)解:点平分.理由如下:
如解图,过点作交的延长线于点,
为的中点,为的中点,
是的中位线,
,,,
.,,
,.
,,
,.
在和中,,
,即点平分.
23.解:(1),;
(2)由题意,得在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况,
第一种情况,当点P在OC上时,点P移动的时间是:;
第二种情况,当点P在BA上时,点P移动的时间是:.
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6s;
(3)设点P移动的时间为.如解图1所示,
的面积是10,,即,
解得,此时;
如解图2所示,
的面积是10,,即,
解得,,此时;
如解图3所示,
的面积是10,,即,
解得,此时;
如解图4所示,
的面积是10,,即,
解得,此时.
综上所述,满足条件的时间的值为或或或.
同课章节目录
