河南省沈丘县全峰完中华东师大版八年级数学上册课件:13-2-5 全等三角形的判定(共17张PPT)
文档属性
| 名称 | 河南省沈丘县全峰完中华东师大版八年级数学上册课件:13-2-5 全等三角形的判定(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-21 00:00:00 | ||
图片预览






文档简介
课件17张PPT。备课人:董长喜13.2.5全等三角形的判定(sss)教学目标1.理解“边边边”的内容。
2.运用“边边边”证明三角形全等。思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
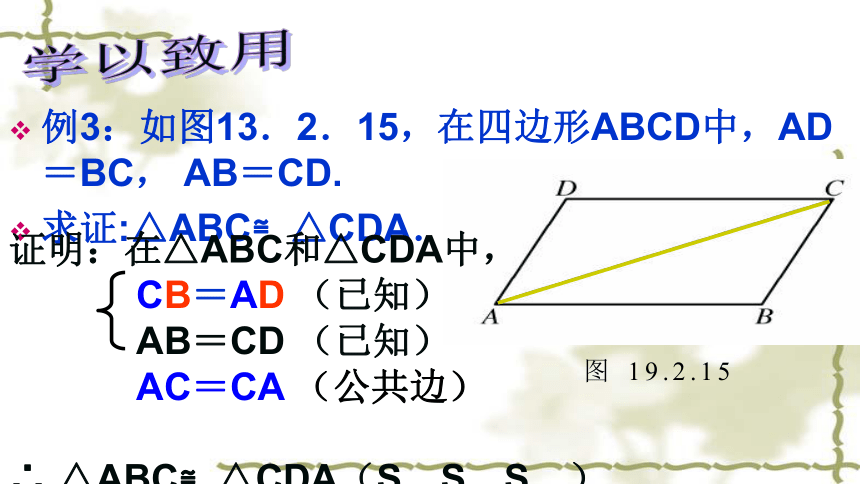
如果将上面的三个角换成三条边,结果又如何呢?不一定,如下面的两个三角形就不全等。做一做:如图13.2.12,已知三条线段,以这三条线段为边,画一个三角形.完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现?发现:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的.全等三角形的判定(sss)边边边公理: 三边 对应 相等的两个三角形全等.(SSS)应用表达式:(如图)在△ABC与△DEF中∴ △ABC≌△DEF (SSS)例3:如图13.2.15,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
学以致用1、已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C练习提升提示:连结BD后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。一定
(S.A.S)不一定一定
(A.S.A)一定
(A.A.S)不一定一定
(S.S.S)
判定三角形全等至少有一组边练习:
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△BCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?全等(SAS)全等(SSS)不能判定全等。全等(SSS等)1、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D巩固提高练习提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。
2、已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D证明:连结AC在△ABC与△ADC中∴ △ABC≌△ADC (SSS)∴∠B=∠D(全等三角形对应角相等)(公共边)3、已知:如图.点B、 E、 C、 F在同一条直
线上, AB = DE , AC = DF,BE = CF
求证: ∠A = ∠D提示:因为BE+CE=CF+CE,即BC=EF,所以由SSS得⊿ABC≌⊿DEF,所以∠A = ∠D(全等三角形对应角相等)
4、已知:如图.AB = DC , AC = DB,
OA = OD
求证:∠A = ∠D
证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(SSS)
∴ ∠A = ∠D(全等三角形对应角相等)5、已知:如图,△ABC是一个钢架,AB=AC,
AD是连结A与BC中点D的支架.
求证:AD⊥BC证明:在△ABD与△ACD中∴ △ABD≌ △ACD (SSS)∴AD⊥BC (垂直定义)∴∠1 = ∠BDC=900 (平角定义)(公共边)∴∠1 = ∠2 (全等三角形的对应角相等)想一想这节课你有什么收获?请说出目前判定三角形全等的4种方法:SAS,ASA,AAS,SSS布置作业73页练习1,2题
2.运用“边边边”证明三角形全等。思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
如果将上面的三个角换成三条边,结果又如何呢?不一定,如下面的两个三角形就不全等。做一做:如图13.2.12,已知三条线段,以这三条线段为边,画一个三角形.完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现?发现:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的.全等三角形的判定(sss)边边边公理: 三边 对应 相等的两个三角形全等.(SSS)应用表达式:(如图)在△ABC与△DEF中∴ △ABC≌△DEF (SSS)例3:如图13.2.15,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
学以致用1、已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C练习提升提示:连结BD后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。一定
(S.A.S)不一定一定
(A.S.A)一定
(A.A.S)不一定一定
(S.S.S)
判定三角形全等至少有一组边练习:
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△BCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?全等(SAS)全等(SSS)不能判定全等。全等(SSS等)1、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D巩固提高练习提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。
2、已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D证明:连结AC在△ABC与△ADC中∴ △ABC≌△ADC (SSS)∴∠B=∠D(全等三角形对应角相等)(公共边)3、已知:如图.点B、 E、 C、 F在同一条直
线上, AB = DE , AC = DF,BE = CF
求证: ∠A = ∠D提示:因为BE+CE=CF+CE,即BC=EF,所以由SSS得⊿ABC≌⊿DEF,所以∠A = ∠D(全等三角形对应角相等)
4、已知:如图.AB = DC , AC = DB,
OA = OD
求证:∠A = ∠D
证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(SSS)
∴ ∠A = ∠D(全等三角形对应角相等)5、已知:如图,△ABC是一个钢架,AB=AC,
AD是连结A与BC中点D的支架.
求证:AD⊥BC证明:在△ABD与△ACD中∴ △ABD≌ △ACD (SSS)∴AD⊥BC (垂直定义)∴∠1 = ∠BDC=900 (平角定义)(公共边)∴∠1 = ∠2 (全等三角形的对应角相等)想一想这节课你有什么收获?请说出目前判定三角形全等的4种方法:SAS,ASA,AAS,SSS布置作业73页练习1,2题
