精致教学理念在数学课堂教学中的运用-以算法案例拓展课(中国剩余定理)为例
文档属性
| 名称 | 精致教学理念在数学课堂教学中的运用-以算法案例拓展课(中国剩余定理)为例 |

|
|
| 格式 | zip | ||
| 文件大小 | 130.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-21 00:00:00 | ||
图片预览


文档简介
精致教学理念在数学课堂教学中的运用
------以算法案例拓展课(中国剩余定理)为例
深圳市龙翔学校高中部数学教师欧阳文丰撰写
导言:我校在邓继新教育工作室的领导下,高 ( http: / / www.21cnjy.com )中部精致班认真贯彻精致教学理念,提倡课堂教学优化教学观念、优化教学目标、优化教学内容、优化教学结构、优化教学方法、优化教学氛围共六个优化思想。本文作者以算法案例拓展课(中国剩余定理)为例,探讨精致教学理念在数学课堂教学中的运用。
一、问题情境
1.孙子不知其数问题
( http: / / www.21cnjy.com / )
2.孙子问题的现代数学描述(引导学生建立数学模型)
“孙子问题”相当于求满足x,y,z为正整数的
不定方程组 ( http: / / www.21cnjy.com / ) m的一个正整数解.
二、探究问题的解决方法
1、 学生活动:尝试集合列举法;
三三数之剩二: 2,5,8,11,14,17,20,23,26,29,32,35,…,3x+2
五五数之剩三: 3,8,13,18,23,28,33,38,43,48,53,58, …,5y+3
七七数之剩二: 2,9,16,23,30,37,44,51,58,65,72,79, …,7z+2
从上面的列举中得知, 这个孙子问题的最小自然数解是23。
温馨提示:此方法思路的优点是容易想得到,但是缺点是列举繁琐。再者,如果所求解的数是比较大的话,还不容易找得到。
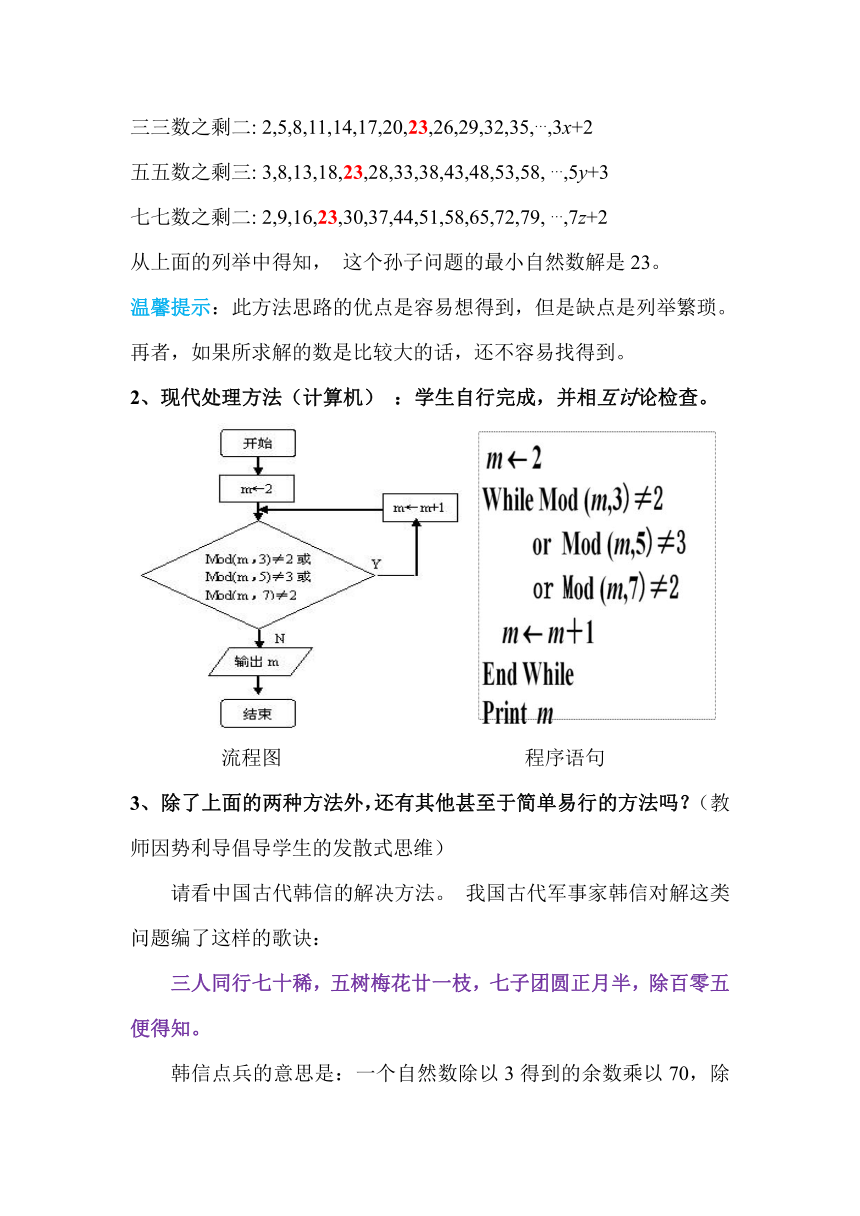
2、现代处理方法(计算机) :学生自行完成,并相互讨论检查。
( http: / / www.21cnjy.com / )
流程图 程序语句
3、 除了上面的两种方法外,还有其他甚至于简单易行的方法吗?(教师因势利导倡导学生的发散式思维)
请看中国古代韩信的解决方法。 我国古代军事家韩信对解这类问题编了这样的歌诀:
三人同行七十稀,五树梅花廿一枝,七子团圆正月半,除百零五便得知。
韩信点兵的意思是:一个自然数除以3得到的余 ( http: / / www.21cnjy.com )数乘以70,除以5得到的余数乘以21,除以7得到的余数乘以15,积相加。如果和大于105,连续减105,直到小于105为止,这样得到的最小自然数,就是所求的结果。
韩信点兵的具体解题思路如下所示:
能同时被5和7整除,还被3除余1的最小整数是:[5,7] ×K, 显然K最小是2。 所以[5,7] ×2=70。
能同时被3和7整除,还被5除余1的最小整数是:[3,7] ×K, 显然K最小是1。 所以[3,7] ×1=21。
能同时被3和5整除,还被7除余1的最小整数是:[3,5] ×K, 显然K最小是1。 所以[3,5] ×1=15。
所以, 一个自然数除以3得到的余数乘以70 ( http: / / www.21cnjy.com ),除以5得到的余数乘以21,除以7得到的余数乘以15,积相加。如果和大于105,连续减105,直到小于105为止,这样得到的最小自然数,就是所求的结果。
三、 典型例题学习(以小组为单位,让学生通过合作学习,领会韩信点兵的解题思路。)
1、 例1 一个数除以3余2,除以5余3,除以7余2。求适合这些条件的最小自然数。
解:能同时被5和7整除,还被3除余1的最小整数是:[5,7] ×K, 显然K最小是2。 所以[5,7] ×2=70。
能同时被3和7整除,还被5除余1的最小整数是:[3,7] ×K, 显然K最小是1。 所以[3,7] ×1=21。
能同时被3和5整除,还被7除余1的最小整数是:[3,5] ×K, 显然K最小是1。 所以[3,5] ×1=15。
所以, 2×70+3×21+2×15 =233, 233- [3, 5, 7] ×2=233-105×2=23。
答:适合这些条件的最小自然数是23。
变式练习1: 一筐苹果 ( http: / / www.21cnjy.com ),如果按5个一堆放, 最后多出3个. 如果按6个一堆放, 最后多出4个. 如果按7个一堆放, 还多出1个. 这筐苹果至少有多少个?
解:能同时被6和7整除,还被5除余1的最小整数是:[6,7] ×K, 显然K最小是3。 所以[6,7] ×3=126。
能同时被5和7整除,还被6除余1的最小整数是:[5,7] ×K, 显然K最小是5。 所以[5,7] ×5=175。
能同时被5和6整除,还被7除余1的最小整数是:[5,6] ×K, 显然K最小是4。 所以[5,6] ×4=120。
所以, 3×126+4×175+1×120=1198, 1198- [5, 6, 7] ×5=1198-210×5=148。
答:这筐苹果至少有148个。
变式练习2:中国古代还流传一个萧何计粮 ( http: / / www.21cnjy.com )的歌诀。九宫山上十一泉, 十一泉涌九宫山,山泉汇合翻五滚,去百加个便了然。 试证明萧何计粮的正确性。
解:萧何计粮的含义是:除以9的余数 ( http: / / www.21cnjy.com )乘以11,除以11的余数乘以9,积相加。 再计算和的5倍,最后去掉百位及以上的数字,添加到个位上后就是所求的最小自然数。
能被11整除,还被9除余1的最小整数是:11 ×K, 显然K最小是5。 所以11 ×5=55。
能被9整除,还被11除余1的最小整数是:9 ×K, 显然K最小是5。 所以9 ×5=45。
所以,一个自然数除以9得到的余数乘 ( http: / / www.21cnjy.com )以55,除以11得到的余数乘以45,积相加。去掉百位及以上的数字,添加到个位上的意思是:如果和大于99,连续减99,直到小于99为止,这样得到的最小自然数,就是所求的结果。
2、 例2 在10000以内,除以3余2,除以7余3,除以11余4的数有几个?
解: 能同时被7和11整除,还被3除余1的最小整数是:[7,11] ×K, 显然K最小是2。 所以[7,11] ×2=154。
能同时被3和11整除,还被7除余1的最小整数是:[3,11] ×K, 显然K最小是3。 所以[3,11] ×3=99。
能同时被3和7整除,还被11除余1的最小整数是:[3,7] ×K, 显然K最小是10。 所以[3,7] ×10=210。
所以, 2×154+3×99+4×210 =1445, 符合题意的数是:1445- [3, 7, 11] ×6=59。
因为[3, 7, 11]=231,所以符合题 ( http: / / www.21cnjy.com )意的数是以59为首项,公差是231的等差数列。(10000-59)÷231=43……8,所以在10000以内符合题意的数共有43+1=44个。
答:在10000以内符合题意的数共有44个。
四、课堂小结
1.孙子不知数问题的求解算法—中国剩余定理;
2.现代数学处理方法是利用循环结构实现整数的搜索;
3、中国古代韩信点兵的解题思路。
五、 课后练习
1、求满足除以5余1,除以7余3,除以8余5的最小的自然数。
2、一个两位数,用它除58余2,除73余3,除85余1,这个两位数是多少?
3、在小于1000的自然数中,除以4余3,除以5余2,除以7余4的最大的自然数是几?
结束语:本节课是以问题情境 ( http: / / www.21cnjy.com )启发学生认识新的问题,进而导入课题。在探究活动中,采用循序渐进引导学生发散式思维,以学生自主式学习,从多维度思考问题,鼓励学生思想活跃,勇于探索。在教师因势利导的前提下,介绍韩信点兵的歌诀,敦促学生理解韩信点兵的解题思路。在典型例题学习的环节中,以学生合作学习的方式,加深对韩信点兵的解题思路的理解。此次课堂教学是通过以学生为主体,以教师为主导,以合作、探究学习的课改教学新模式的教学实践,达到优化课堂教学过程和方法,提高课堂教学的有效性目的。以中国古代数学文化的陶冶,培养学生的爱国主义情怀和数学素养。
(作者系深圳市龙翔学校高中部数学教师欧阳文丰)
------以算法案例拓展课(中国剩余定理)为例
深圳市龙翔学校高中部数学教师欧阳文丰撰写
导言:我校在邓继新教育工作室的领导下,高 ( http: / / www.21cnjy.com )中部精致班认真贯彻精致教学理念,提倡课堂教学优化教学观念、优化教学目标、优化教学内容、优化教学结构、优化教学方法、优化教学氛围共六个优化思想。本文作者以算法案例拓展课(中国剩余定理)为例,探讨精致教学理念在数学课堂教学中的运用。
一、问题情境
1.孙子不知其数问题
( http: / / www.21cnjy.com / )
2.孙子问题的现代数学描述(引导学生建立数学模型)
“孙子问题”相当于求满足x,y,z为正整数的
不定方程组 ( http: / / www.21cnjy.com / ) m的一个正整数解.
二、探究问题的解决方法
1、 学生活动:尝试集合列举法;
三三数之剩二: 2,5,8,11,14,17,20,23,26,29,32,35,…,3x+2
五五数之剩三: 3,8,13,18,23,28,33,38,43,48,53,58, …,5y+3
七七数之剩二: 2,9,16,23,30,37,44,51,58,65,72,79, …,7z+2
从上面的列举中得知, 这个孙子问题的最小自然数解是23。
温馨提示:此方法思路的优点是容易想得到,但是缺点是列举繁琐。再者,如果所求解的数是比较大的话,还不容易找得到。
2、现代处理方法(计算机) :学生自行完成,并相互讨论检查。
( http: / / www.21cnjy.com / )
流程图 程序语句
3、 除了上面的两种方法外,还有其他甚至于简单易行的方法吗?(教师因势利导倡导学生的发散式思维)
请看中国古代韩信的解决方法。 我国古代军事家韩信对解这类问题编了这样的歌诀:
三人同行七十稀,五树梅花廿一枝,七子团圆正月半,除百零五便得知。
韩信点兵的意思是:一个自然数除以3得到的余 ( http: / / www.21cnjy.com )数乘以70,除以5得到的余数乘以21,除以7得到的余数乘以15,积相加。如果和大于105,连续减105,直到小于105为止,这样得到的最小自然数,就是所求的结果。
韩信点兵的具体解题思路如下所示:
能同时被5和7整除,还被3除余1的最小整数是:[5,7] ×K, 显然K最小是2。 所以[5,7] ×2=70。
能同时被3和7整除,还被5除余1的最小整数是:[3,7] ×K, 显然K最小是1。 所以[3,7] ×1=21。
能同时被3和5整除,还被7除余1的最小整数是:[3,5] ×K, 显然K最小是1。 所以[3,5] ×1=15。
所以, 一个自然数除以3得到的余数乘以70 ( http: / / www.21cnjy.com ),除以5得到的余数乘以21,除以7得到的余数乘以15,积相加。如果和大于105,连续减105,直到小于105为止,这样得到的最小自然数,就是所求的结果。
三、 典型例题学习(以小组为单位,让学生通过合作学习,领会韩信点兵的解题思路。)
1、 例1 一个数除以3余2,除以5余3,除以7余2。求适合这些条件的最小自然数。
解:能同时被5和7整除,还被3除余1的最小整数是:[5,7] ×K, 显然K最小是2。 所以[5,7] ×2=70。
能同时被3和7整除,还被5除余1的最小整数是:[3,7] ×K, 显然K最小是1。 所以[3,7] ×1=21。
能同时被3和5整除,还被7除余1的最小整数是:[3,5] ×K, 显然K最小是1。 所以[3,5] ×1=15。
所以, 2×70+3×21+2×15 =233, 233- [3, 5, 7] ×2=233-105×2=23。
答:适合这些条件的最小自然数是23。
变式练习1: 一筐苹果 ( http: / / www.21cnjy.com ),如果按5个一堆放, 最后多出3个. 如果按6个一堆放, 最后多出4个. 如果按7个一堆放, 还多出1个. 这筐苹果至少有多少个?
解:能同时被6和7整除,还被5除余1的最小整数是:[6,7] ×K, 显然K最小是3。 所以[6,7] ×3=126。
能同时被5和7整除,还被6除余1的最小整数是:[5,7] ×K, 显然K最小是5。 所以[5,7] ×5=175。
能同时被5和6整除,还被7除余1的最小整数是:[5,6] ×K, 显然K最小是4。 所以[5,6] ×4=120。
所以, 3×126+4×175+1×120=1198, 1198- [5, 6, 7] ×5=1198-210×5=148。
答:这筐苹果至少有148个。
变式练习2:中国古代还流传一个萧何计粮 ( http: / / www.21cnjy.com )的歌诀。九宫山上十一泉, 十一泉涌九宫山,山泉汇合翻五滚,去百加个便了然。 试证明萧何计粮的正确性。
解:萧何计粮的含义是:除以9的余数 ( http: / / www.21cnjy.com )乘以11,除以11的余数乘以9,积相加。 再计算和的5倍,最后去掉百位及以上的数字,添加到个位上后就是所求的最小自然数。
能被11整除,还被9除余1的最小整数是:11 ×K, 显然K最小是5。 所以11 ×5=55。
能被9整除,还被11除余1的最小整数是:9 ×K, 显然K最小是5。 所以9 ×5=45。
所以,一个自然数除以9得到的余数乘 ( http: / / www.21cnjy.com )以55,除以11得到的余数乘以45,积相加。去掉百位及以上的数字,添加到个位上的意思是:如果和大于99,连续减99,直到小于99为止,这样得到的最小自然数,就是所求的结果。
2、 例2 在10000以内,除以3余2,除以7余3,除以11余4的数有几个?
解: 能同时被7和11整除,还被3除余1的最小整数是:[7,11] ×K, 显然K最小是2。 所以[7,11] ×2=154。
能同时被3和11整除,还被7除余1的最小整数是:[3,11] ×K, 显然K最小是3。 所以[3,11] ×3=99。
能同时被3和7整除,还被11除余1的最小整数是:[3,7] ×K, 显然K最小是10。 所以[3,7] ×10=210。
所以, 2×154+3×99+4×210 =1445, 符合题意的数是:1445- [3, 7, 11] ×6=59。
因为[3, 7, 11]=231,所以符合题 ( http: / / www.21cnjy.com )意的数是以59为首项,公差是231的等差数列。(10000-59)÷231=43……8,所以在10000以内符合题意的数共有43+1=44个。
答:在10000以内符合题意的数共有44个。
四、课堂小结
1.孙子不知数问题的求解算法—中国剩余定理;
2.现代数学处理方法是利用循环结构实现整数的搜索;
3、中国古代韩信点兵的解题思路。
五、 课后练习
1、求满足除以5余1,除以7余3,除以8余5的最小的自然数。
2、一个两位数,用它除58余2,除73余3,除85余1,这个两位数是多少?
3、在小于1000的自然数中,除以4余3,除以5余2,除以7余4的最大的自然数是几?
结束语:本节课是以问题情境 ( http: / / www.21cnjy.com )启发学生认识新的问题,进而导入课题。在探究活动中,采用循序渐进引导学生发散式思维,以学生自主式学习,从多维度思考问题,鼓励学生思想活跃,勇于探索。在教师因势利导的前提下,介绍韩信点兵的歌诀,敦促学生理解韩信点兵的解题思路。在典型例题学习的环节中,以学生合作学习的方式,加深对韩信点兵的解题思路的理解。此次课堂教学是通过以学生为主体,以教师为主导,以合作、探究学习的课改教学新模式的教学实践,达到优化课堂教学过程和方法,提高课堂教学的有效性目的。以中国古代数学文化的陶冶,培养学生的爱国主义情怀和数学素养。
(作者系深圳市龙翔学校高中部数学教师欧阳文丰)
