湘教版八年级数学上册第五章 二次根式(小结与复习课件)
文档属性
| 名称 | 湘教版八年级数学上册第五章 二次根式(小结与复习课件) |  | |
| 格式 | zip | ||
| 文件大小 | 210.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-23 09:05:03 | ||
图片预览






文档简介
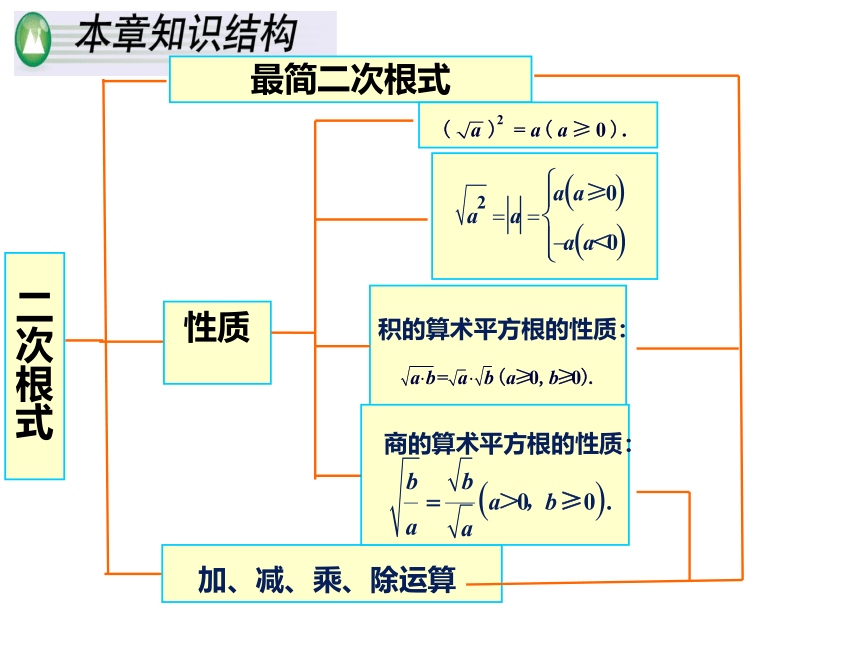
课件16张PPT。二次根式小结与复习第五章 1. 二次根式 在实数范围内有意义
的条件是什么?
2. 二次根式有哪些性质?
4. 如何进行二次根式的加、减、乘、
除运算? 举例说明什么叫最简二次根式,试写出一个二次根式并将它化简. 1. 二次根式 在实数范围内有意义,必须满足 .
2.学习了二次根式以后,代数式可看成是把数和表示
数的字母用运算符号(加、减、乘、除、乘方和开方)
连接而成的式子.
二次根式的概念形如 (a 0)的式子叫做二次根式1.二次根式的定义:2.二次根式的识别:(1).被开方数(2).根指数是2例.下列各式中那些是二次根式?
那些不是?为什么?⑧⑦⑥⑤④①②③二次根式的性质(1).(2).(3).题型1:确定二次根式中被开方数所含字母
的取值范围.1. 当 X ____时, 有意义。 3.求下列二次根式中字母的取值范围解得 - 5≤x<3说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组) ≤3a=4题型2:二次根式的非负性的应用.4.已知: + =0,求 x-y 的值.5.(2005.湖北黄冈市)已知x,y为实数,且
+ 3(y-2)2 =0,则x-y的值为( )
A.3 B.-3 C.1 D.-1解:由题意,得 x-4=0 且 2x+y=0解得 x=4,y=-8∴x-y=4-(-8)= 4+ 8 =12D 抢答:判断下列二次根式是否是最简二次根式,并说明理由。 满足下列两个条件的二次根式,叫做最简二次根式(1)被开方数的因数是整数,因式是整式(2)被开方数中不含能开得尽方的因数或因式例1:把下列各式化成最简二次根式例2:把下列各式化成最简二次根式(a≥0)(1)判断下列各式是否成立?你认为成立的,请在括号里
打 “√”,不成立的,请在括号里打 “×”
(2)你判断完以上各题之后,能猜想这类式子
具有什么规律?(3)试用数学知识说明你所提出的猜想是正确
的吗?探索性练习:拓展1结 束
的条件是什么?
2. 二次根式有哪些性质?
4. 如何进行二次根式的加、减、乘、
除运算? 举例说明什么叫最简二次根式,试写出一个二次根式并将它化简. 1. 二次根式 在实数范围内有意义,必须满足 .
2.学习了二次根式以后,代数式可看成是把数和表示
数的字母用运算符号(加、减、乘、除、乘方和开方)
连接而成的式子.
二次根式的概念形如 (a 0)的式子叫做二次根式1.二次根式的定义:2.二次根式的识别:(1).被开方数(2).根指数是2例.下列各式中那些是二次根式?
那些不是?为什么?⑧⑦⑥⑤④①②③二次根式的性质(1).(2).(3).题型1:确定二次根式中被开方数所含字母
的取值范围.1. 当 X ____时, 有意义。 3.求下列二次根式中字母的取值范围解得 - 5≤x<3说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组) ≤3a=4题型2:二次根式的非负性的应用.4.已知: + =0,求 x-y 的值.5.(2005.湖北黄冈市)已知x,y为实数,且
+ 3(y-2)2 =0,则x-y的值为( )
A.3 B.-3 C.1 D.-1解:由题意,得 x-4=0 且 2x+y=0解得 x=4,y=-8∴x-y=4-(-8)= 4+ 8 =12D 抢答:判断下列二次根式是否是最简二次根式,并说明理由。 满足下列两个条件的二次根式,叫做最简二次根式(1)被开方数的因数是整数,因式是整式(2)被开方数中不含能开得尽方的因数或因式例1:把下列各式化成最简二次根式例2:把下列各式化成最简二次根式(a≥0)(1)判断下列各式是否成立?你认为成立的,请在括号里
打 “√”,不成立的,请在括号里打 “×”
(2)你判断完以上各题之后,能猜想这类式子
具有什么规律?(3)试用数学知识说明你所提出的猜想是正确
的吗?探索性练习:拓展1结 束
同课章节目录
