湘教版九年级数学上册课件 5.1 总体平均数与方差的估计
文档属性
| 名称 | 湘教版九年级数学上册课件 5.1 总体平均数与方差的估计 |  | |
| 格式 | zip | ||
| 文件大小 | 453.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-23 09:07:26 | ||
图片预览











文档简介
课件30张PPT。5.1 总体平均数与方差的估计1.计算样本平均数和方差使学生认识到只有样本容量足够大,才能比较准确地反映总体的特性,这样的样本才可靠,体会只有可靠的样本,才能用样本去估计总体.
2.通过实例,使学生体会用样本估计总体的思想,能够根据统计结果作出合理的判断和推测,能与同学进行交流,用清晰的语言表达自己的观点. 复习回顾1、总体是指什么?2、什么叫样本?什么叫样本容量?3、什么是简单随机样本? 我们知道在选取样本时应注意的问题,其一是所选取的样本必须具有代表性,其二是所选取的样本的容量应该足够大,这样的样本才能反映总体的特性,所选取的样本才比较可靠. 随机抽样调查是了解总体情况的一种重要的数学方法,抽样是它的一个关键,原来我们学过了简单的随机抽样方法,即用抽签的方法来选取样本,这使总体的每个个体都有相等的机会被选入样本.判断下面这些抽样调查选取样本的方法是否合适,若不合适,请说明理由.
(1)为调查江苏省的环境污染情况,调查了长江以南的南京市、常州市、苏州市、镇江市、无锡市的环境污染情况.
(2)从100名学生中,随机抽取2名学生,测量他们的身高来估算这100名学生的平均身高.
(3)从一批灯泡中随机抽取50个进行试验,估算这批灯泡的使用寿命.
(4)为了解观众对中央电视台第一套节目的收视率,对所有上因特网的家庭进行在线调查.解:(1)不合适.因为调查对象在总体中必须有代表性,现在所调查的这些地方的环境污染情况仅仅代表了长江以南地区,并不能代表整个江苏省的环境污染情况.
(2)不合适.因为抽样调查时所抽取的样本要足够大,现在只抽取了2名学生的身高,不能用来估算100名学生的平均身高.(3)合适.
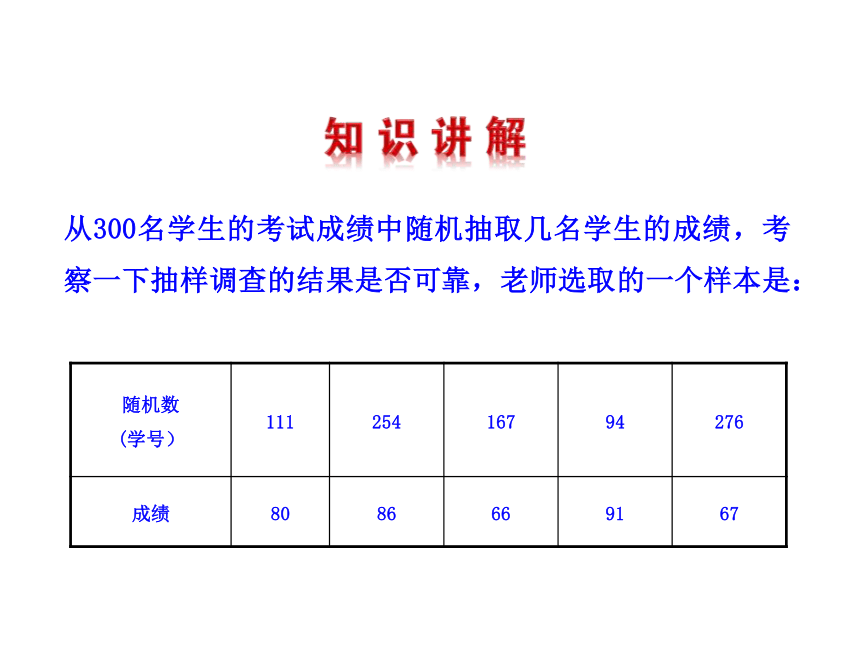
(4)不合适.虽然调查的家庭很多,但仅仅增加调查的数量,不一定能够提高调查质量,本题中所调查的仅代表上因特网的家庭,不能代表全部的家庭,因此这样的抽样调查不具有普遍代表性.从300名学生的考试成绩中随机抽取几名学生的成绩,考察一下抽样调查的结果是否可靠,老师选取的一个样本是:它的频数分布直方图、平均成绩和方差分别如下:另外,同学们也分别选取了一些样本,它们同样也包含五个个体,如下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和方差,如图所示: 样本平均成绩为
81分,
方差为22.4样本平均成绩为
74.2分,
方差为9.36 从以上三张图比较来看,它们之间存在明显的差异,平均数和方差与总体的平均数与方差也相差甚远,显然这样选择的样本不能反映总体的特性,是不可靠的.【规律方法】当样本中个体太少时,样本的平均数、方差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、方差与总体的平均数、方差相当接近.
对于简单随机样本,可以用样本的百分比去估计总体的百分比(收视率、次品率、合格率等).也可以用样本的平均数去估计总体的平均数;用样本的方差去估计总体的方差.北京在这30天的空气污染指数及质量级别,如表所示:【例题】体会用样本估计总体的合理性经比较可以发现,虽然从样本获得的数据与总体的不完全一致,但这样的误差还是可以接受
的,是一个较好的估计. 随着样本容量(样本中包含的个体的个数)的增加,由样本得出的平均数往往会更接近总体的平均数,数学家已经证明随机抽样方法是科学而可靠的. 对于估计总体特性这类问题,数学上的一般做法是给出具有一定可靠程度的一个估计值的范围.加权平均数的求法问题1:在计算20个男同学的平均身高时,小华先将所有数据按由小到大的顺序排列,如表所示:然后,他这样计算这20个学生的平均身高:小华这样计算平均数可以吗?为什么?问题2:假设你们年级共有四个班级,各班的男同学人数和平均身高如表所示.小强这样计算全年级男同学的平均身高:小强这样计算平均数可以吗?为什么?为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:
(1)在这个问题中,总体、个体、样本和样本容量各是什
么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.【跟踪训练】解:(1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20.
(2)在20个数据中,10出现了6次,次数最多,所以众数是10 米.
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9 米和10 米,所以中位数是9.5 米.样本平均数是9.4 米.新知探究从总体中抽取样本,然后通过对样本的分析,去推断总体的情况,是统计的基本思想。用样本平均数、样本方差分别去估计总体平均数、总体方差是这一思想的一个体现。实践和理论都证明:对于简单随机样本,在大多数情况下,当样本容量足够大时,这种估计是合理的。说一说1、如何估计某城市所有家庭一年内平均丢弃的塑料袋个数2、在检查甲、乙两种棉花的纤维长度时,如何估计哪种棉花的纤维长度比较整齐?可以进行简单随机抽样,然后用样本去推断总体。动脑筋某农科院在某地区选择了自然条件相同的两个实验区,用相同的管理技术试种甲、乙两个品种的水稻各100亩。如何确定哪个品种的水稻在该地区更有推广价值呢?提示:为了选择合适的稻种,我们应关心这两种水稻的哪些方面的数据呢?例题一台机床生产一种直径为40mm的圆柱形零件,在正常生产时,生产的零件的直径的方差不超过0.01.如果超过0.01,则机床应检修调整。
下表是某日8:30---9:30及10:00---11:00两个时段中各随机抽取10个零件量出的直径的数值(单位:mm):39.839.88:30—9:3010:30—11:304039.840.140.240.24039.840.140.24039.940.24040.14039.94039.9试判断在这两个时段内生产是否正常?例题39.839.88:30—9:3010:30—11:304039.840.140.240.24039.840.140.24039.940.24040.14039.94039.9X1=(40+39.8×4+40.1×2+40.2×3)÷10=40在10:30—11:30这段时间内生产的零件中,随机抽取的10个零件的直径的平均数 x2、方差s22分别为:可以推断在8:30—9:30机床生产不正常,在10:30—11:30机床生产正常。1.(南通·中考)某纺织厂从10万件同类产品中随机抽取了100件进行质检,发现其中有5件不合格,那么估计该厂这10万件产品中合格品约为( )
A.9.5万件 B.9万件
C.9500件 D.5000件
答案:A2.2013年因干旱影响,某市鼓励居民节约用水,为了解居民用水情况,在某小区随机抽查了20户家庭的月用水量,结果如下表:
则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6吨 B.平均数是5.8吨
C.众数是6吨 D.方差是4
答案:D 3.(嘉兴·中考)李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25㎏,200㎏ B.2.5㎏,100㎏
C.0.25㎏,100㎏ D.2.5㎏,200㎏
答案:C1.一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确.相应地,搜集、整理、计算数据的工作量也就越大.因此,在实际工作中,样本容量既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价的大小.
2.随机抽样是经过数学证明了的可靠的方法,它对于估计总体特征是很有帮助的.
2.通过实例,使学生体会用样本估计总体的思想,能够根据统计结果作出合理的判断和推测,能与同学进行交流,用清晰的语言表达自己的观点. 复习回顾1、总体是指什么?2、什么叫样本?什么叫样本容量?3、什么是简单随机样本? 我们知道在选取样本时应注意的问题,其一是所选取的样本必须具有代表性,其二是所选取的样本的容量应该足够大,这样的样本才能反映总体的特性,所选取的样本才比较可靠. 随机抽样调查是了解总体情况的一种重要的数学方法,抽样是它的一个关键,原来我们学过了简单的随机抽样方法,即用抽签的方法来选取样本,这使总体的每个个体都有相等的机会被选入样本.判断下面这些抽样调查选取样本的方法是否合适,若不合适,请说明理由.
(1)为调查江苏省的环境污染情况,调查了长江以南的南京市、常州市、苏州市、镇江市、无锡市的环境污染情况.
(2)从100名学生中,随机抽取2名学生,测量他们的身高来估算这100名学生的平均身高.
(3)从一批灯泡中随机抽取50个进行试验,估算这批灯泡的使用寿命.
(4)为了解观众对中央电视台第一套节目的收视率,对所有上因特网的家庭进行在线调查.解:(1)不合适.因为调查对象在总体中必须有代表性,现在所调查的这些地方的环境污染情况仅仅代表了长江以南地区,并不能代表整个江苏省的环境污染情况.
(2)不合适.因为抽样调查时所抽取的样本要足够大,现在只抽取了2名学生的身高,不能用来估算100名学生的平均身高.(3)合适.
(4)不合适.虽然调查的家庭很多,但仅仅增加调查的数量,不一定能够提高调查质量,本题中所调查的仅代表上因特网的家庭,不能代表全部的家庭,因此这样的抽样调查不具有普遍代表性.从300名学生的考试成绩中随机抽取几名学生的成绩,考察一下抽样调查的结果是否可靠,老师选取的一个样本是:它的频数分布直方图、平均成绩和方差分别如下:另外,同学们也分别选取了一些样本,它们同样也包含五个个体,如下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和方差,如图所示: 样本平均成绩为
81分,
方差为22.4样本平均成绩为
74.2分,
方差为9.36 从以上三张图比较来看,它们之间存在明显的差异,平均数和方差与总体的平均数与方差也相差甚远,显然这样选择的样本不能反映总体的特性,是不可靠的.【规律方法】当样本中个体太少时,样本的平均数、方差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、方差与总体的平均数、方差相当接近.
对于简单随机样本,可以用样本的百分比去估计总体的百分比(收视率、次品率、合格率等).也可以用样本的平均数去估计总体的平均数;用样本的方差去估计总体的方差.北京在这30天的空气污染指数及质量级别,如表所示:【例题】体会用样本估计总体的合理性经比较可以发现,虽然从样本获得的数据与总体的不完全一致,但这样的误差还是可以接受
的,是一个较好的估计. 随着样本容量(样本中包含的个体的个数)的增加,由样本得出的平均数往往会更接近总体的平均数,数学家已经证明随机抽样方法是科学而可靠的. 对于估计总体特性这类问题,数学上的一般做法是给出具有一定可靠程度的一个估计值的范围.加权平均数的求法问题1:在计算20个男同学的平均身高时,小华先将所有数据按由小到大的顺序排列,如表所示:然后,他这样计算这20个学生的平均身高:小华这样计算平均数可以吗?为什么?问题2:假设你们年级共有四个班级,各班的男同学人数和平均身高如表所示.小强这样计算全年级男同学的平均身高:小强这样计算平均数可以吗?为什么?为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:
(1)在这个问题中,总体、个体、样本和样本容量各是什
么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.【跟踪训练】解:(1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20.
(2)在20个数据中,10出现了6次,次数最多,所以众数是10 米.
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9 米和10 米,所以中位数是9.5 米.样本平均数是9.4 米.新知探究从总体中抽取样本,然后通过对样本的分析,去推断总体的情况,是统计的基本思想。用样本平均数、样本方差分别去估计总体平均数、总体方差是这一思想的一个体现。实践和理论都证明:对于简单随机样本,在大多数情况下,当样本容量足够大时,这种估计是合理的。说一说1、如何估计某城市所有家庭一年内平均丢弃的塑料袋个数2、在检查甲、乙两种棉花的纤维长度时,如何估计哪种棉花的纤维长度比较整齐?可以进行简单随机抽样,然后用样本去推断总体。动脑筋某农科院在某地区选择了自然条件相同的两个实验区,用相同的管理技术试种甲、乙两个品种的水稻各100亩。如何确定哪个品种的水稻在该地区更有推广价值呢?提示:为了选择合适的稻种,我们应关心这两种水稻的哪些方面的数据呢?例题一台机床生产一种直径为40mm的圆柱形零件,在正常生产时,生产的零件的直径的方差不超过0.01.如果超过0.01,则机床应检修调整。
下表是某日8:30---9:30及10:00---11:00两个时段中各随机抽取10个零件量出的直径的数值(单位:mm):39.839.88:30—9:3010:30—11:304039.840.140.240.24039.840.140.24039.940.24040.14039.94039.9试判断在这两个时段内生产是否正常?例题39.839.88:30—9:3010:30—11:304039.840.140.240.24039.840.140.24039.940.24040.14039.94039.9X1=(40+39.8×4+40.1×2+40.2×3)÷10=40在10:30—11:30这段时间内生产的零件中,随机抽取的10个零件的直径的平均数 x2、方差s22分别为:可以推断在8:30—9:30机床生产不正常,在10:30—11:30机床生产正常。1.(南通·中考)某纺织厂从10万件同类产品中随机抽取了100件进行质检,发现其中有5件不合格,那么估计该厂这10万件产品中合格品约为( )
A.9.5万件 B.9万件
C.9500件 D.5000件
答案:A2.2013年因干旱影响,某市鼓励居民节约用水,为了解居民用水情况,在某小区随机抽查了20户家庭的月用水量,结果如下表:
则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6吨 B.平均数是5.8吨
C.众数是6吨 D.方差是4
答案:D 3.(嘉兴·中考)李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25㎏,200㎏ B.2.5㎏,100㎏
C.0.25㎏,100㎏ D.2.5㎏,200㎏
答案:C1.一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确.相应地,搜集、整理、计算数据的工作量也就越大.因此,在实际工作中,样本容量既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价的大小.
2.随机抽样是经过数学证明了的可靠的方法,它对于估计总体特征是很有帮助的.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
