华师大版八年级数学上册课件:14.2 勾股定理的应用(共21张PPT)
文档属性
| 名称 | 华师大版八年级数学上册课件:14.2 勾股定理的应用(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 403.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-23 22:29:09 | ||
图片预览






文档简介
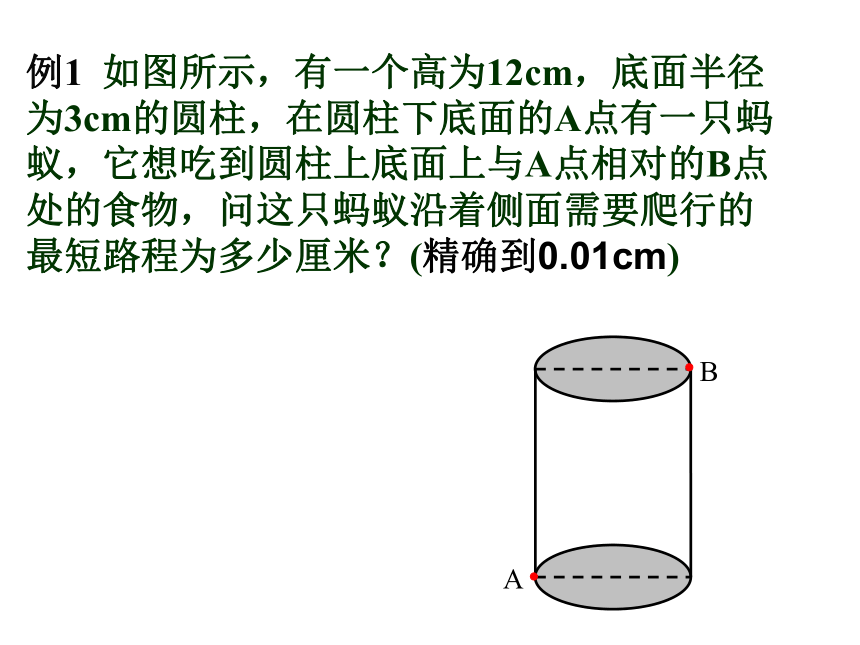
课件21张PPT。勾股定理的应用例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(精确到0.01cm)例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(精确到0.01cm)小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
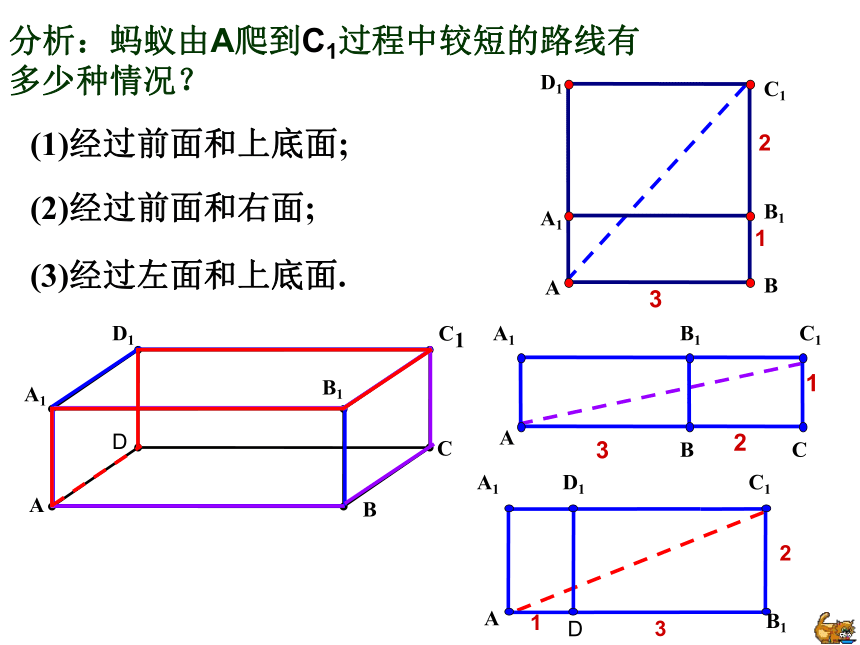
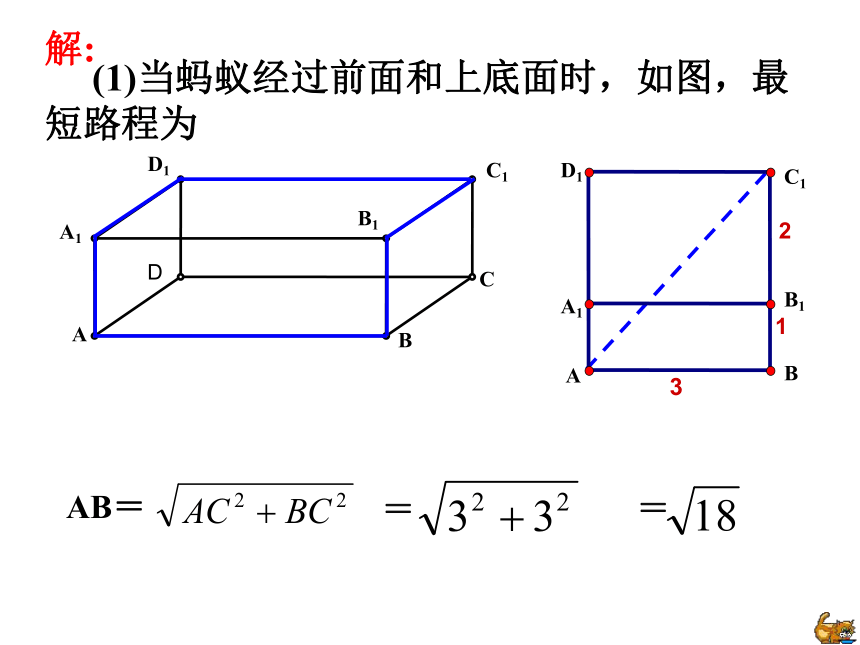
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?变式一: 如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?变式一: 如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面由A爬到C1需要爬行的最短路程又是多少呢?变式二:BCDB1C1D1A1分析:蚂蚁由A爬到C1过程中较短的路线有 多少种情况?(1)经过前面和上底面;(2)经过前面和右面;(3)经过左面和上底面.BCDB1C1D1A1 (1)当蚂蚁经过前面和上底面时,如图,最短路程为解:AB===BCDB1C1D1A1(2)当蚂蚁经过前面和右面时,如图,最短路程为AB===BCDB1C1D1A1(3)当蚂蚁经过左面和上底面时,如图,最短路程为AC1===BCDB1C1D1A1练习1:如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.
练习2:如图,长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.例2:在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?DABC练习:
教材P63. T12解:设水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
在Rt△ABC中,∠ACB=90°
AB2=BC2+AC2
(X+1)2=52+X2
X=12
X+1 =12+1=13(米)
经检验,符合题意
答:水池的深度为12米,芦苇高为13米.例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 2米2.3米OC┏D分析:H2米2.3米 由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 解CD=CH=0.6+2.3=2.9(米)>2.5(米).答:卡车能通过厂门.在Rt△OCD中,∠CDO=90°由勾股定理得==0.6米,2米2.3米例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 练习1:在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?.DBCA练习2: 两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?甲(A)乙(B)┏
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?变式一: 如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?变式一: 如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面由A爬到C1需要爬行的最短路程又是多少呢?变式二:BCDB1C1D1A1分析:蚂蚁由A爬到C1过程中较短的路线有 多少种情况?(1)经过前面和上底面;(2)经过前面和右面;(3)经过左面和上底面.BCDB1C1D1A1 (1)当蚂蚁经过前面和上底面时,如图,最短路程为解:AB===BCDB1C1D1A1(2)当蚂蚁经过前面和右面时,如图,最短路程为AB===BCDB1C1D1A1(3)当蚂蚁经过左面和上底面时,如图,最短路程为AC1===BCDB1C1D1A1练习1:如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.
练习2:如图,长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.例2:在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?DABC练习:
教材P63. T12解:设水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
在Rt△ABC中,∠ACB=90°
AB2=BC2+AC2
(X+1)2=52+X2
X=12
X+1 =12+1=13(米)
经检验,符合题意
答:水池的深度为12米,芦苇高为13米.例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 2米2.3米OC┏D分析:H2米2.3米 由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 解CD=CH=0.6+2.3=2.9(米)>2.5(米).答:卡车能通过厂门.在Rt△OCD中,∠CDO=90°由勾股定理得==0.6米,2米2.3米例3:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 练习1:在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?.DBCA练习2: 两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?甲(A)乙(B)┏
