人教版九年级数学上册课件:23.2 中心对称
文档属性
| 名称 | 人教版九年级数学上册课件:23.2 中心对称 |  | |
| 格式 | ppt | ||
| 文件大小 | 582.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-24 09:10:19 | ||
图片预览


文档简介
(共17张PPT)
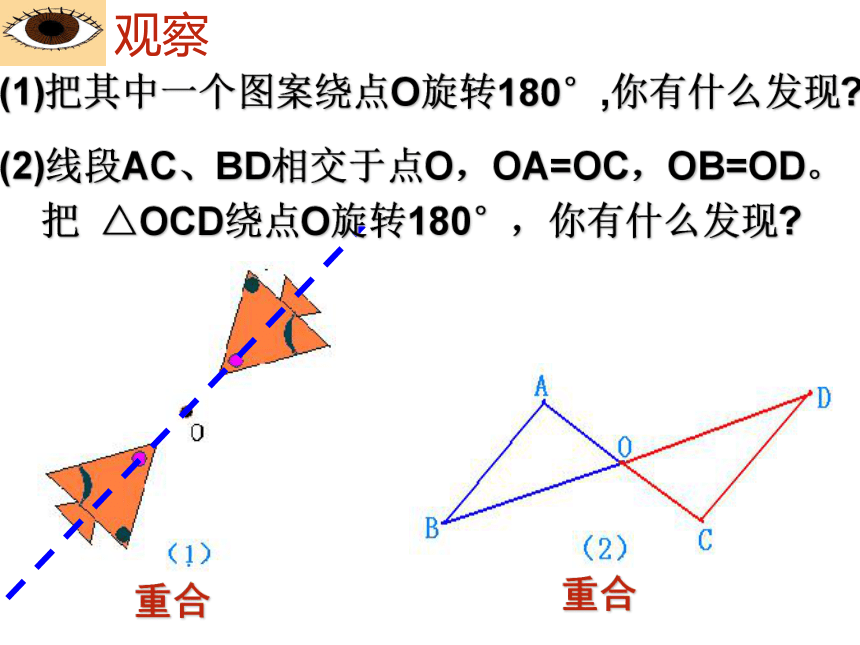
(1)把其中一个图案绕点O旋转180°,你有什么发现
重合
重合
观察
(2)线段AC、BD相交于点O,OA=OC,OB=OD。
把 △OCD绕点O旋转180°,你有什么发现
A
C
B
A
C
B
A
C
B
A
D
E
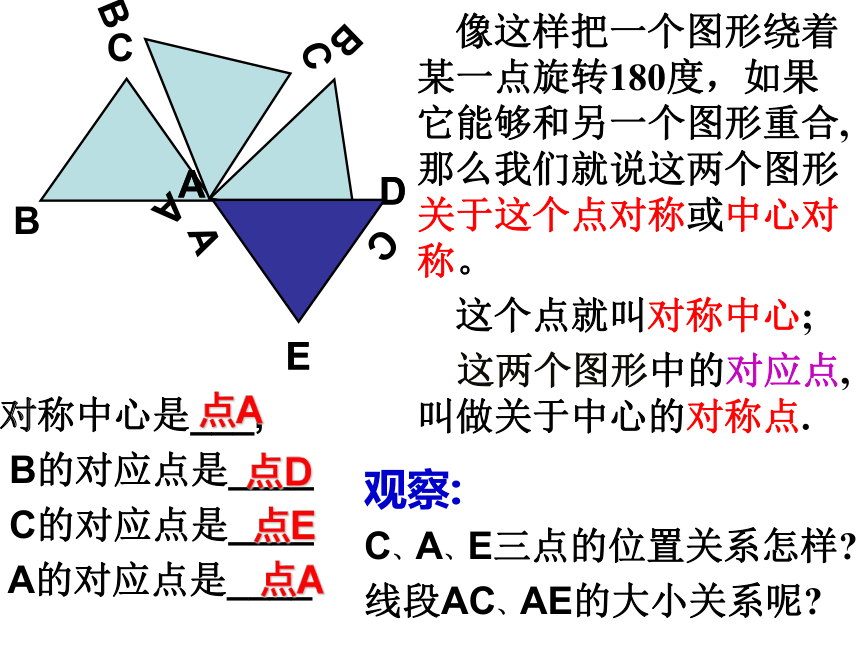
像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么我们就说这两个图形关于这个点对称或中心对称。
这个点就叫对称中心;
这两个图形中的对应点,叫做关于中心的对称点.
A
D
E
对称中心是___,
B的对应点是____
C的对应点是____
A的对应点是____
点A
点D
点E
点A
观察:
C、A、E三点的位置关系怎样
线段AC、AE的大小关系呢
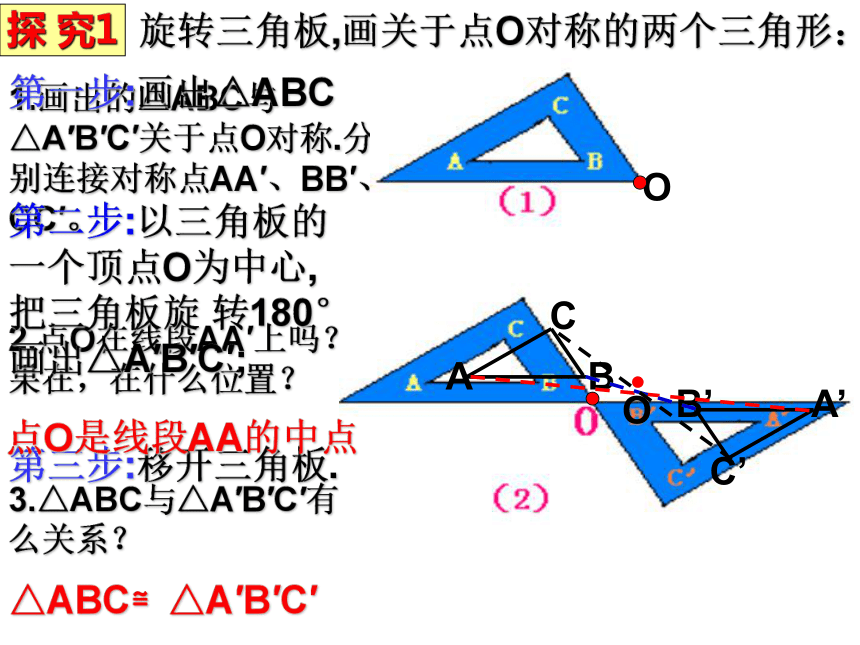
探 究1
旋转三角板,画关于点O对称的两个三角形:
1.画出的△ABC与△A′B′C′关于点O对称.分别连接对称点AA′、BB′、CC′。
2.点O在线段AA′上吗?如果在,在什么位置?
3.△ABC与△A′B′C′有什么关系?
第一步:画出△ABC
第二步:以三角板的一个顶点O为中心,
把三角板旋 转180°,画出△A′B′C′;
第三步:移开三角板.
O
.
A
A’
C
C’
O
B
B’
点O是线段AA的中点
△ABC≌△A′B′C′
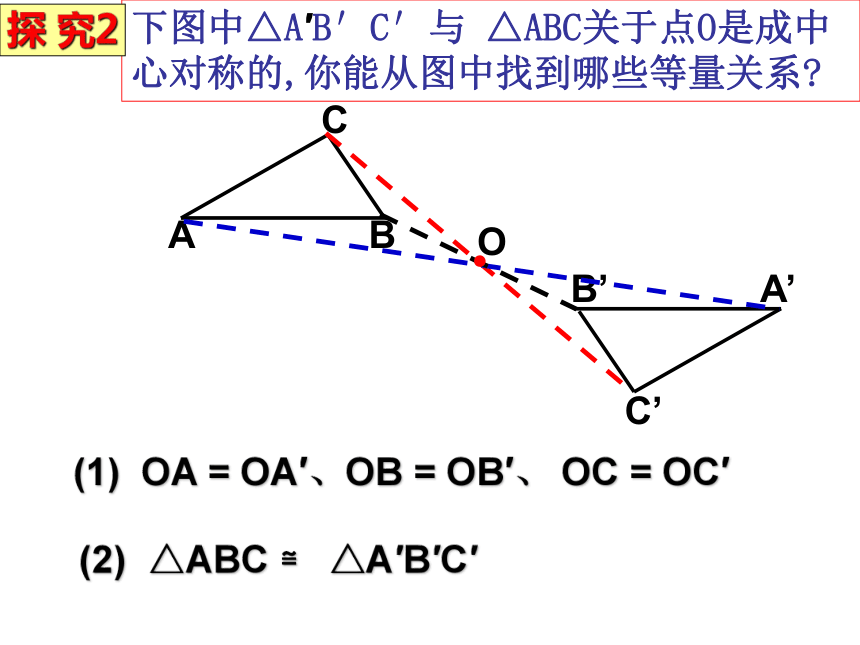
下图中△A′B′C′与 △ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
A
A’
C
C’
O
B
B’
.
(1) OA = OA′、OB = OB′、 OC = OC′
(2) △ABC ≌ △A′B′C′
探 究2
归纳中心对称的性质:
(1)关于中心对称的两个图形,对称点所连线段都经过_______,并且被对称中心_____。
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称。
(2)关于中心对称的两个图形是_____。
全等形
对称中心
平分
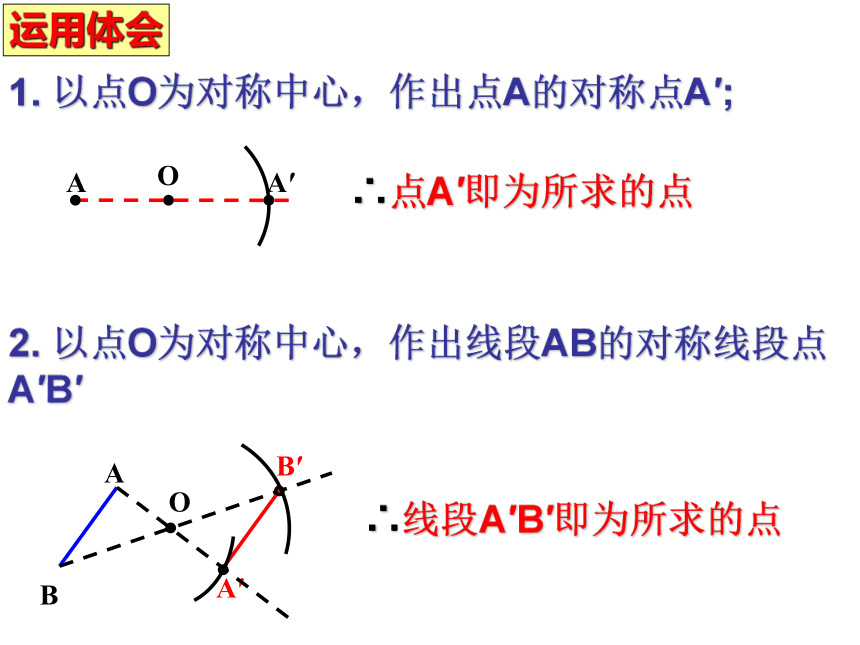
运用体会
1. 以点O为对称中心,作出点A的对称点A′;
A
O
A′
∴点A′即为所求的点
2. 以点O为对称中心,作出线段AB的对称线段点A′B′
A
A′
B′
B
O
∴线段A′B′即为所求的点
例1 如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
∴ △A′B′C′即为所求的三角形。
例2. 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。
A
B
A’
C’
B’
D’
D
O
C
∴四边形A1B1C1D1即为所求的图形。
1.画一个与已知四边形ABCD中心对称图形
(1) 以顶点A为对称中心;
(2) 以BC边的中点O为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
N
提高
练习
A’
B’
C’
O
A
B
C
2.如图,已知等边三角形ABC和点O,画△A’B’C’,使△A’B’C’和△ABC关于点O成中心对称。
A
B
C
A’
B’
C’
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
解法一:连结BB’,用刻度尺找出BB’的中点O,则点O即为所求.
A
B
C
A’
B’
C’
O
A
B
C
A’
B’
C’
O
解法二:连结BB’,CC’交于点O,则点O即为所求.
练习
1.分别画出下列图形关于点O的中心对称图形
2.图中的两个四边形关于某点中心对称,找出
它们的对称中心.
想一想
中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折
(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
聚焦中考.如图是某设计师在方格纸中设计图案
的一部分,请你帮他完成余下的工作 :
(1)作出关于直线AB的轴对称图形
(2)将你画出的部分连同原图形绕点O逆时
针旋转90°.
(3)发挥你的想象,给得到的图案适当涂上阴影,让图案变得更加美丽
A
B
O
小结
1.中心对称是旋转的特殊形式,旋转角
是180°.
2.中心对称的性质
(1) 成中心对称的两个图形全等,
(2) 连接对应点的的线段经过对称中心,
并且被对称中心平分.
(1)把其中一个图案绕点O旋转180°,你有什么发现
重合
重合
观察
(2)线段AC、BD相交于点O,OA=OC,OB=OD。
把 △OCD绕点O旋转180°,你有什么发现
A
C
B
A
C
B
A
C
B
A
D
E
像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么我们就说这两个图形关于这个点对称或中心对称。
这个点就叫对称中心;
这两个图形中的对应点,叫做关于中心的对称点.
A
D
E
对称中心是___,
B的对应点是____
C的对应点是____
A的对应点是____
点A
点D
点E
点A
观察:
C、A、E三点的位置关系怎样
线段AC、AE的大小关系呢
探 究1
旋转三角板,画关于点O对称的两个三角形:
1.画出的△ABC与△A′B′C′关于点O对称.分别连接对称点AA′、BB′、CC′。
2.点O在线段AA′上吗?如果在,在什么位置?
3.△ABC与△A′B′C′有什么关系?
第一步:画出△ABC
第二步:以三角板的一个顶点O为中心,
把三角板旋 转180°,画出△A′B′C′;
第三步:移开三角板.
O
.
A
A’
C
C’
O
B
B’
点O是线段AA的中点
△ABC≌△A′B′C′
下图中△A′B′C′与 △ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
A
A’
C
C’
O
B
B’
.
(1) OA = OA′、OB = OB′、 OC = OC′
(2) △ABC ≌ △A′B′C′
探 究2
归纳中心对称的性质:
(1)关于中心对称的两个图形,对称点所连线段都经过_______,并且被对称中心_____。
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称。
(2)关于中心对称的两个图形是_____。
全等形
对称中心
平分
运用体会
1. 以点O为对称中心,作出点A的对称点A′;
A
O
A′
∴点A′即为所求的点
2. 以点O为对称中心,作出线段AB的对称线段点A′B′
A
A′
B′
B
O
∴线段A′B′即为所求的点
例1 如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
∴ △A′B′C′即为所求的三角形。
例2. 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。
A
B
A’
C’
B’
D’
D
O
C
∴四边形A1B1C1D1即为所求的图形。
1.画一个与已知四边形ABCD中心对称图形
(1) 以顶点A为对称中心;
(2) 以BC边的中点O为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
N
提高
练习
A’
B’
C’
O
A
B
C
2.如图,已知等边三角形ABC和点O,画△A’B’C’,使△A’B’C’和△ABC关于点O成中心对称。
A
B
C
A’
B’
C’
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
解法一:连结BB’,用刻度尺找出BB’的中点O,则点O即为所求.
A
B
C
A’
B’
C’
O
A
B
C
A’
B’
C’
O
解法二:连结BB’,CC’交于点O,则点O即为所求.
练习
1.分别画出下列图形关于点O的中心对称图形
2.图中的两个四边形关于某点中心对称,找出
它们的对称中心.
想一想
中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折
(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
聚焦中考.如图是某设计师在方格纸中设计图案
的一部分,请你帮他完成余下的工作 :
(1)作出关于直线AB的轴对称图形
(2)将你画出的部分连同原图形绕点O逆时
针旋转90°.
(3)发挥你的想象,给得到的图案适当涂上阴影,让图案变得更加美丽
A
B
O
小结
1.中心对称是旋转的特殊形式,旋转角
是180°.
2.中心对称的性质
(1) 成中心对称的两个图形全等,
(2) 连接对应点的的线段经过对称中心,
并且被对称中心平分.
同课章节目录
