沪教版八年级数学下册试题 22.3特殊平行四边形试卷(含答案)
文档属性
| 名称 | 沪教版八年级数学下册试题 22.3特殊平行四边形试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览

文档简介
22.3特殊平行四边形
一、单选题
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别相等 B.两组对边分别平行
C.两条对角线相等 D.两条对角线互相垂直
2.如图,在菱形中,对角线,相交于点,若,则的度数为( )
A. B. C. D.
3.下列四个命题中,真命题是( )
A.对角线垂直且相等的四边形是菱形
B.对角线互相垂直平分的四边形是正方形
C.一组邻边相等的平行四边形是正方形
D.对角线相等且互相平分的四边形是矩形
4.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )
A. B. C.9 D.12
5.如图,E是矩形的边上一点,,则等于( )
A. B. C. D.
6.如图,在正方形 中, 是 上的一点,且 ,则 的度数是()
A.20° B.22.5° C.30° D.45°
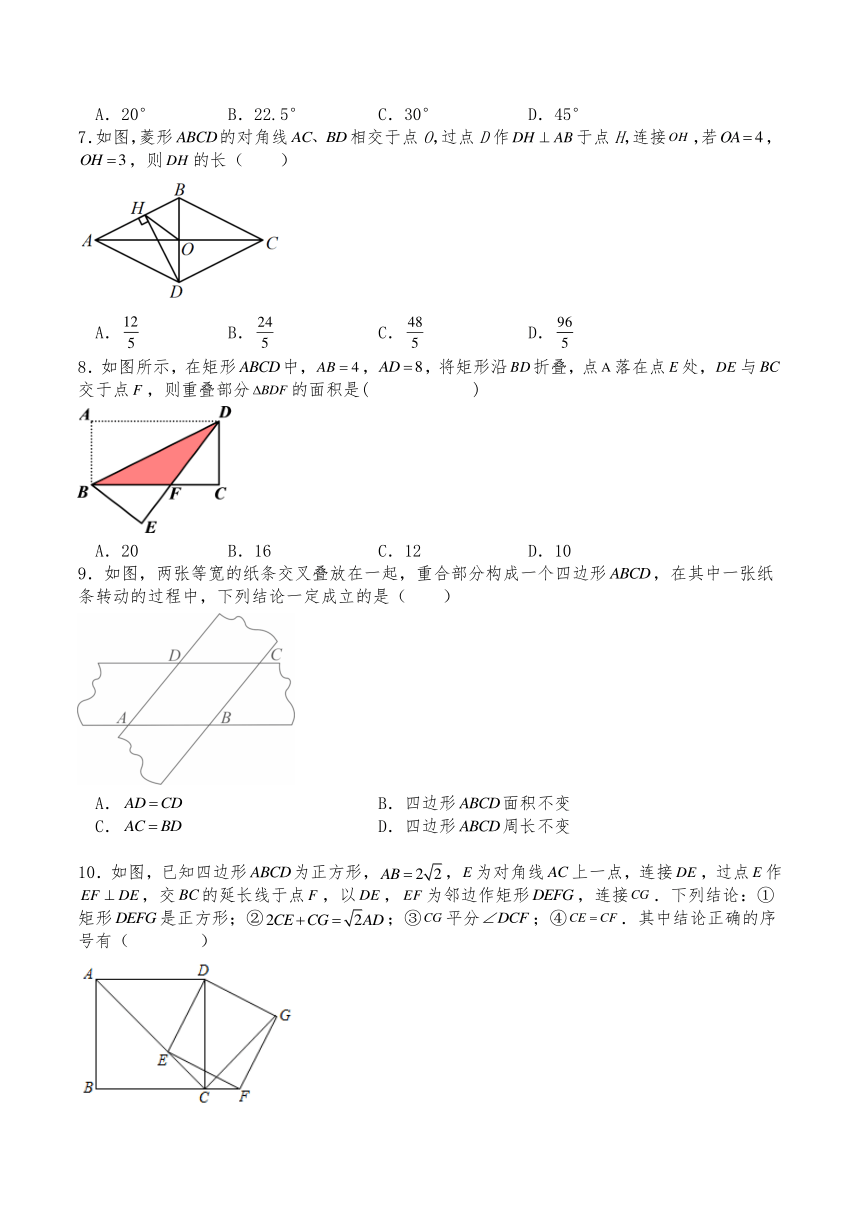
7.如图,菱形的对角线相交于点O,过点D作于点H,连接,若,,则的长( )
A. B. C. D.
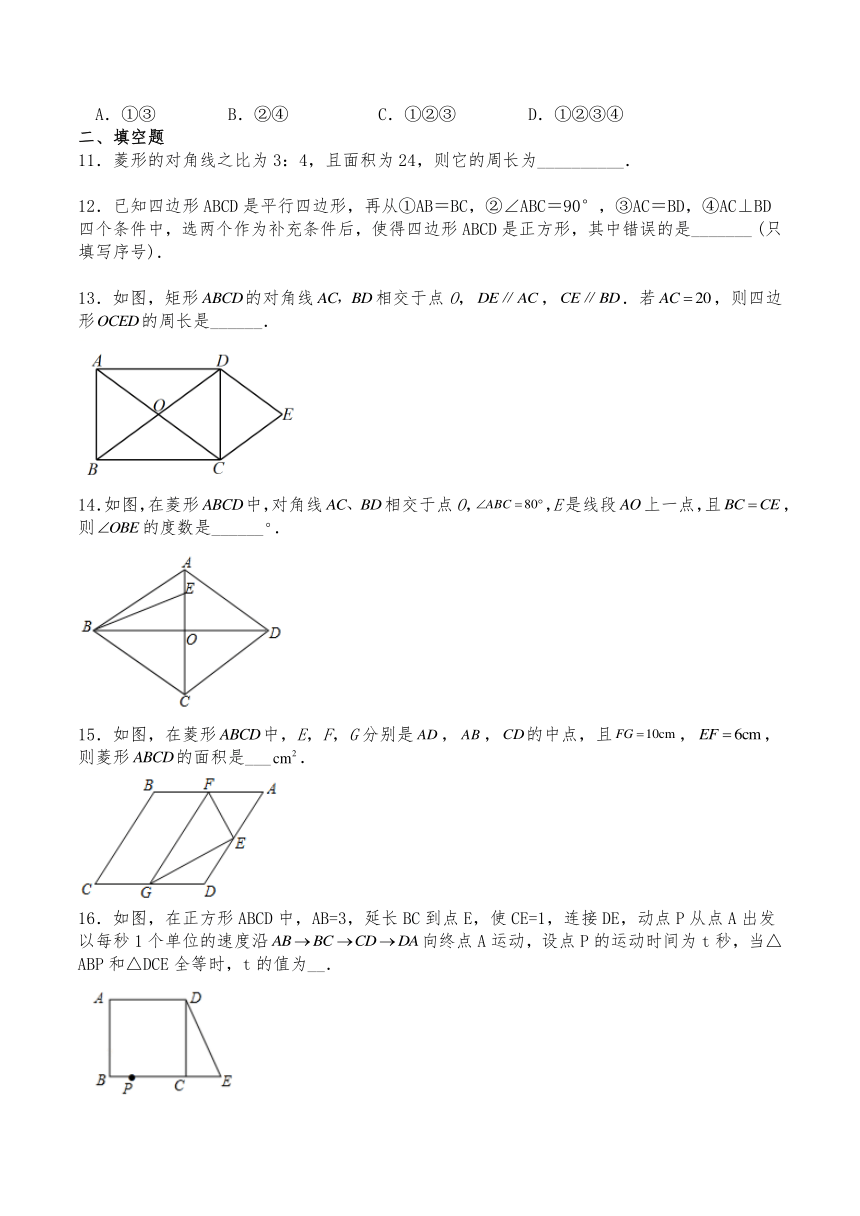
8.如图所示,在矩形中,,,将矩形沿折叠,点落在点处,与交于点,则重叠部分的面积是( )
A.20 B.16 C.12 D.10
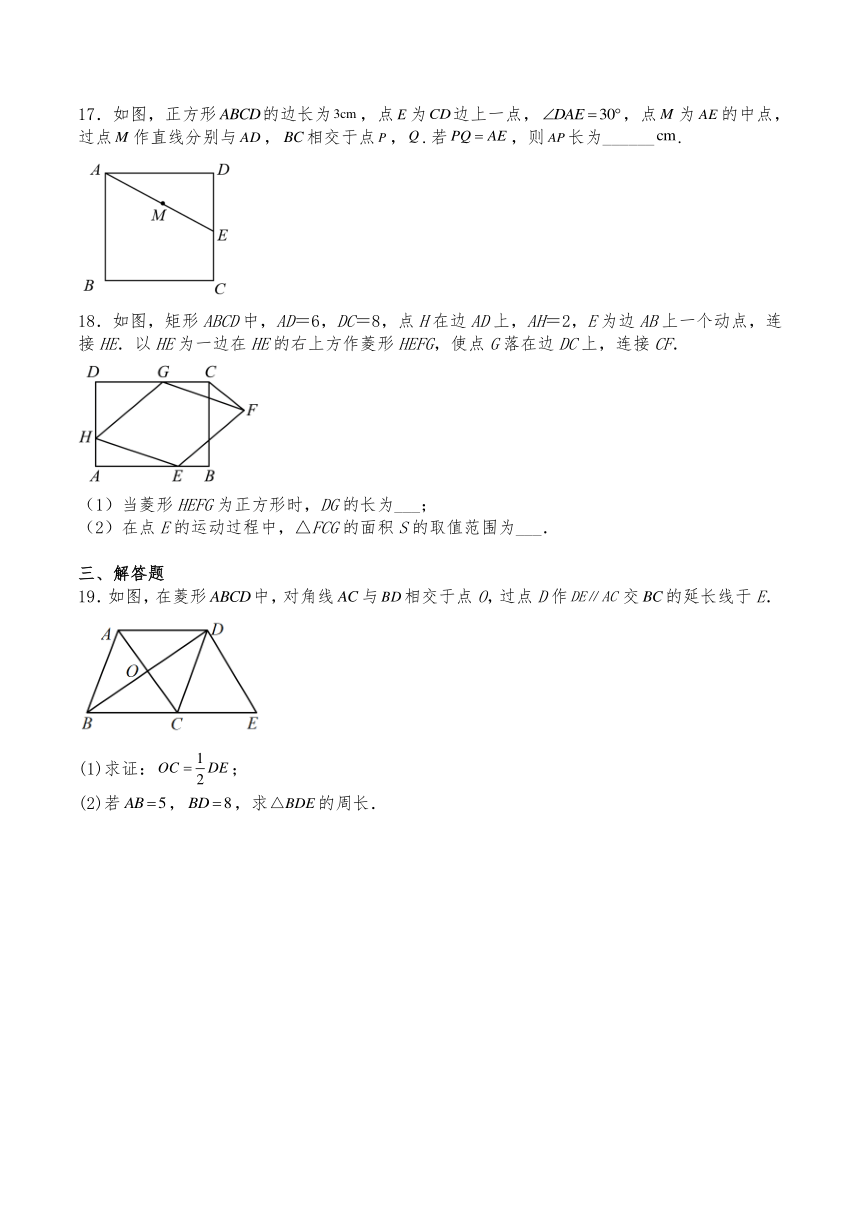
9.如图,两张等宽的纸条交叉叠放在一起,重合部分构成一个四边形,在其中一张纸条转动的过程中,下列结论一定成立的是( )
A. B.四边形面积不变
C. D.四边形周长不变
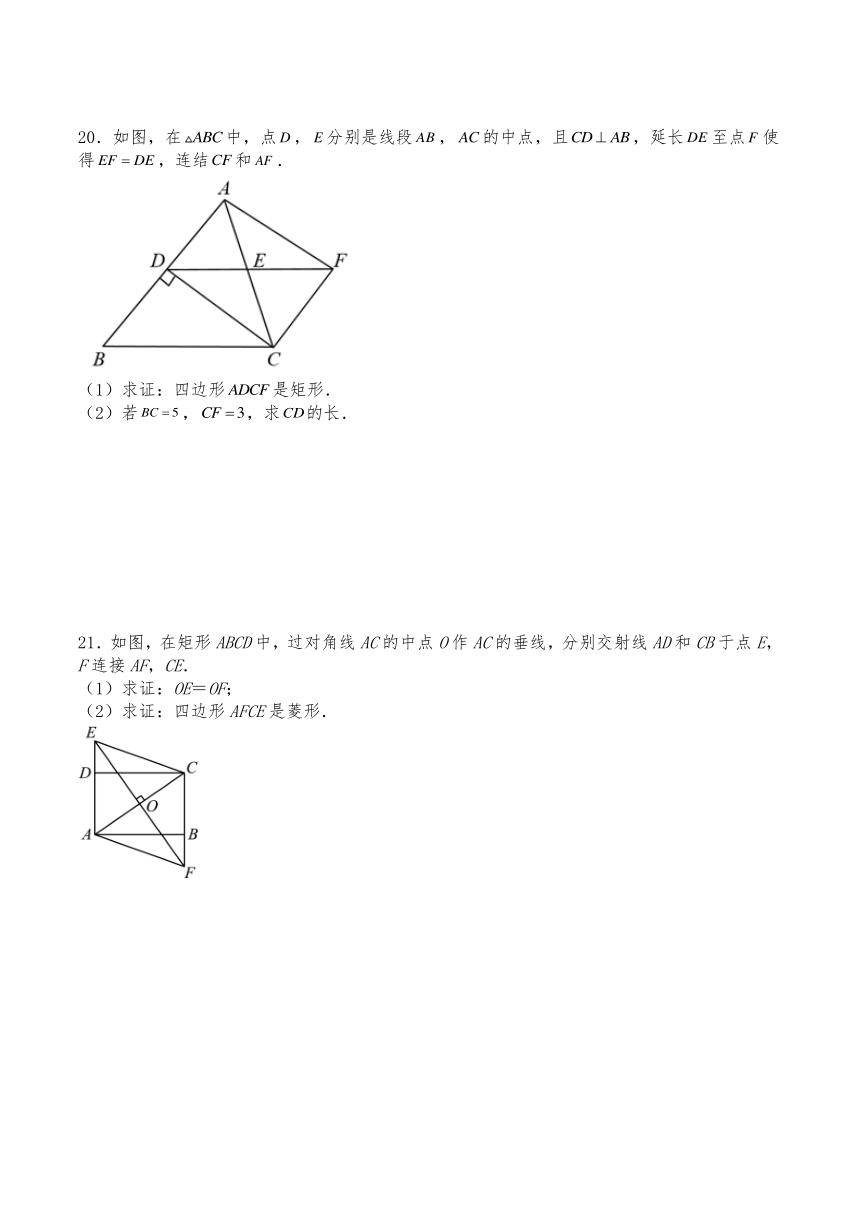
10.如图,已知四边形为正方形,,为对角线上一点,连接,过点作,交的延长线于点,以,为邻边作矩形,连接.下列结论:①矩形是正方形;②;③平分;④.其中结论正确的序号有( )
A.①③ B.②④ C.①②③ D.①②③④
二、填空题
11.菱形的对角线之比为3:4,且面积为24,则它的周长为__________.
12.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_______ (只填写序号).
13.如图,矩形的对角线相交于点O,,.若,则四边形的周长是______.
14.如图,在菱形中,对角线相交于点O,,E是线段上一点,且,则的度数是______.
15.如图,在菱形中,E,F,G分别是,,的中点,且,,则菱形的面积是___.
16.如图,在正方形ABCD中,AB=3,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为__.
17.如图,正方形的边长为,点为边上一点,,点为的中点,过点作直线分别与,相交于点,.若,则长为______.
18.如图,矩形ABCD中,AD=6,DC=8,点H在边AD上,AH=2,E为边AB上一个动点,连接HE.以HE为一边在HE的右上方作菱形HEFG,使点G落在边DC上,连接CF.
(1)当菱形HEFG为正方形时,DG的长为___;
(2)在点E的运动过程中,△FCG的面积S的取值范围为___.
三、解答题
19.如图,在菱形中,对角线与相交于点O,过点D作交的延长线于E.
(1)求证:;
(2)若,,求的周长.
20.如图,在中,点,分别是线段,的中点,且,延长至点使得,连结和.
(1)求证:四边形是矩形.
(2)若,,求的长.
21.如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E,F连接AF,CE.
(1)求证:OE=OF;
(2)求证:四边形AFCE是菱形.
22.如图,菱形ABCD的对角线AC,BD相交于点,过点D作,且,连接,连接交于点.
(1)求证:;
(2)若菱形ABCD的边长为4,,求的长.
23.如图,正方形中,点分别在边上,且,连接相交于点,作,垂足是.
(1)求证:;
(2)求证:.
24.已知,如图,矩形中,,,菱形的三个顶点,,分别在矩形的边,,上,,连接.
(1)若,求证四边形为正方形;
(2)若,求的面积.
25.已知正方形的边长为4,E是上一个动点,以点E为直角顶点,在正方形外侧等腰直角三角形,连结、、.
(1)与的位置关系是__________.
(2)①如图1,当(即点E与点D重合)时,的面积为_________.
②如图2,当(即点E为的中点)时,的面积为________.
③如图3,当时,的面积为_______.
(3)如图4,根据上述计算的结果,当E是上任意一点时,请提出你对面积与正方形的面积之间关系的猜想,并证明你的猜想.
26.如图,在平行四边形 ABCD中,,E,F分别为,的中点,作于点G,的延长线交的延长线于点H.
(1)求证:四边形是菱形.
(2)当时,
①求的长.
②如图2,交于点P,记的面积为,的面积为,则的值为________.
27.如图,已知四边形是正方形,,点E为对角线上一动点,连接.过点E作,交射线点F,以为邻边作矩形.连接.
(1)连接,求证:.
(2)求证:矩形是正方形.
(3)探究:的值是否为定值?若是,请求出这个定值,若不是,请说明理由.
答案
一、单选题
1.C
【分析】分别根据矩形和菱形的性质可得出其对角线性质的不同,可得到答案.
【解析】解:矩形的对角线相等且平分,菱形的对角线垂直且平分,
所以矩形具有而菱形不具有的为对角线相等,
故选:C.
2.B
【分析】根据菱形的性质得到,,再进一步求解即可.
【解析】解:四边形是菱形,
,,
,
,
,
故选B.
3.D
【分析】根据菱形、矩形、正方形的判定定理等知识逐项判定即可.
【解析】解:选项,对角线相等且互相垂直的四边形是菱形,若对角线不互相平分,则不是菱形,故原命题为假命题;
选项,对角线互相平分说明是平行四边形,菱形的判定定理:对角线垂直的平行四边形是菱形,故原命题为假命题;
选项,有一组邻边相等的平行四边形是菱形,故原命题为假命题;
选项,对角线相等且互相平分的四边形是矩形,为真命题;
故选:.
4.B
【分析】根据矩形对角线相等且互相平分的性质和题中的条件易得△AOB为等边三角形,即可得到矩形对角线的长,进而求解即可.
【解析】
如图:AB=6,∠AOB=60°,
∵四边形是矩形,AC,BD是对角线,
∴OA=OB=OC=OD=BD=AC,
在△AOB中,OA=OB,∠AOB=60°,
∴OA=OB=AB=6,BD=2OB=12,
∴BC=.
故选:B.
5.C
【分析】先由矩形证得,从而得,再由等腰三角形的性质求出等腰三角形的底角,再由平行线性质得出结论.
【解析】解:四边形是矩形,
∴
∴
∵,
∴
∴,
∵
∴,
故选:C
6.B
【分析】在正方形中可知∠BAC=45°,由AB=AE,进而求出∠ABE,又知∠ABE+∠EBC=90°,故能求出∠EBC.
【解析】解:在正方形ABCD中,∠BAC=45°,
∵AB=AE,
∴∠ABE=∠AEB=67.5°,
∵∠ABE+∠EBC=90°,
∴∠EBC=22.5°,
故选B.
【点睛】本题主要考查正方形的性质,等腰三角形的性质等知识点,熟练掌握基础知识是解题关键.
7.如图,菱形的对角线相交于点O,过点D作于点H,连接,若,,则的长( )
A. B. C. D.
【答案】B
【分析】根据菱形的性质得O为的中点,再由直角三角形斜边上的中线等于斜边的一半,得的长度,利用勾股定理求得的长,最后由菱形的面积公式求解.
【解析】解:∵四边形是菱形,
∴,
∵,
∴,
∴,
∵,
∴,,
∵,
∴,,
∵,即,
∴.
故选:B.
8.D
【分析】根据折叠的性质可得∠ADB=∠EDB,由平行可得∠ADB=∠CBD,推出∠CBD=∠EDB,设BF为x,在Rt△DCF中,根据勾股定理列出方程求出x,再根据面积公式求出△BDF的面积即可.
【解析】∵AD∥BC,
∴∠ADB=∠CBD,
∵△BDE是△BDA折叠后的图形,
∴∠ADB=∠EDB,
∴∠CBD=∠EDB,
设BF为x,则DF为x,CF为8-x,
在Rt△DCF中,
解得:x=5,
∴S△BDF=.
故选D.
9.A
【分析】两张等宽的纸条的宽为h,根据题意可得,从而得到四边形是平行四边形,再由,可得,进而得到四边形是菱形,即可.
【解析】解∶ 设两张等宽的纸条的宽为h,
∵纸条的对边平行,
∴,
∴四边形是平行四边形,
又∵,
∴,
∴四边形是菱形,
∴,故A选项正确,符合题意,C选项错误,不符合题意;
∵在旋转的过程中,在变化,
∴四边形面积和周长也在变化,故B、D选项错误,不符合题意;
故选:A.
10.A
【分析】过作,过作于,如图所示,根据正方形性质得,,推出四边形是正方形,由矩形性质得,,根据全等三角形的性质得,推出矩形是正方形,故①正确;根据正方形性质得,推出,得到,,由此推出平分,故③正确;进而求得,故②错误;当时,点与点重合,得到不一定等于,故④错误;故选A.
【解析】过作,过作于,如图所示,
∵四边形是正方形,
∴,,
∴,
∴,
∴四边形是正方形,
∴,
∵四边形是矩形,
∴,
∴,
在和中,
,
∴,
∴,
∴矩形是正方形,故①正确;
∴,
∵四边形是正方形
∴,
∴
在和中
∴
∴,
∵
∴平分,故③正确;
∴,故②错误;
当时,点与点重合,
∴不一定等于,故④错误.
故选:A
二、填空题
11.20
【分析】依题意,已知菱形的面积以及对角线之比,首先根据面积公式求出菱形的对角线长,然后利用勾股定理求出菱形的边长.
【解析】解:如图:
由题:,
∴可设,,
∵菱形ABCD的面积为,
∴(舍去),
∴,,
∴,,
∴中,由勾股定理得:,
∴菱形的周长是:.
故答案是:20.
12.②③或①④
【分析】要判定是正方形,则需能判定它既是菱形又是矩形.
【解析】有6种选法:(1)①②:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(2)②③:由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误;
(3)①③:由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(4)②④:由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
(5)①④:由①得有一组邻边相等的平行四边形是菱形,由④得对角线互相垂直的平行四边形是菱形,所以不能得出平行四边形ABCD是正方形,错误;
(6)③④:由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
综上所述:错误的是:②③或①④.
故答案为②③或①④.
13.40
【分析】根据矩形的对角线互相平分且相等,得到,再利用两对边平行的四边形为平行四边形得到四边形为平行四边形,利用邻边相等的平行四边形为菱形得到四边形为菱形,即可求出其周长.
【解析】∵四边形为矩形,
,,且,
∴,
,
∴四边形为平行四边形,
,
∴四边形为菱形,
.
故答案为:40
14.
【分析】由菱形的性质可得,,可得,由三角形内角和定理求得的度数,据此即可求解.
【解析】解:∵四边形是菱形,,
∴,,
∴,
∵,
∴,
∴,
故答案为:.
15.96
【分析】连接,,交点为,与交于点,与交于点,由三角形中位线定理得出,,,,得出,由勾股定理求出的长,根据菱形的面积公式可得出答案.
【解析】解:如图,连接,,交点为,与交于点,与交于点,
四边形是菱形,
,
,,分别是,,的中点,
,,,,
四边形是矩形,
,
,,
,
,,
菱形的面积是.
故答案为96.
16.4或11
【分析】根据运动过程,根据点P运动的位置和全等情况分类讨论,根据全等三角形的性质即可分别求解.
【解析】解:当点P在AB上运动时,显然A、B、P构不成三角形
∴此时不符合题意;
当点P在BC上运动时,
由AB=CD, ∠ABP=∠DCE=90°,显然此时存在△ABP≌△DCE
∴BP=CE
∴t-3=1,即t=4;
当点P在CD上运动时,如下图所示,显然不存在点P,使得△ABP和△DCE全等;
当点P在DA上运动时,如下图所示
由AB=CD, ∠A=∠DCE=90°,显然此时存在△ABP≌△CDE
∴AP=CE=1
∴3×4-t=1
解得t=11.
综上:当△ABP和△DCE全等时,t的值为4或11.
故答案为:4或11.
17.1或2
【分析】根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.
【解析】根据题意画出图形,过点作,交于点,交于点,四边形为正方形,.
在中,,cm,
cm.
根据勾股定理得cm.
为的中点,
cm,
在和中,
,
,.
PN//DC,
,
,即.
在中,,
cm.
由对称性得到 cm,
综上,等于1cm或2cm.
故答案为1或2.
18. 2
【分析】(1)由于四边形ABCD为矩形,四边形HEFG为正方形,那么∠D=∠A=∠GHE=,HG=HE,易证△GDH≌△HAE,得DG=AH=2;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于ABCD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2,进而可求△FCG的面积S的最大值和最小值,从而确定S的取值范围.
【解析】解:(1)如图1,当菱形为正方形时,,,
四边形为矩形,
,
,
,
在和中,
,
,
;
故答案为:2;
(2)如图2,过作,交延长线于,连接,
∵ABCD,
,
∵HEGF,
,
,
在和中,
,
,即无论菱形如何变化,点到直线的距离始终为定值2,
∴,
设,则,
在中,,
,
,
即,
,
,
的最小值为,此时,
的最大值为8时,,
在点的运动过程中,的面积的取值范围为:;
故答案为:;
三、解答题
19.(1)证明:四边形是菱形,
,,,
∵,
∴四边形是平行四边形,
∴,
,
.
(2)解:在菱形中,,
在中,,,
,
,
,
周长.
20.解:(1)∵E是AC中点,
∴,
∵,
∴四边形ADCF是平行四边形,
∵,
∴,
∴四边形ADCF是矩形.
(2)∵四边形ADCF是矩形,
∴,
∵D是AB中点,
∴,
∵,
∴,
∴.
21.解:(1)∵四边形ABCD是矩形,
∴AD//BC,
∴∠EAO=∠FCO,
∵AC的中点是O,
∴OA=OC,
在和中,
,
,
∴OE=OF;
(2)∵OE=OF,AO=CO,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
22.(1)证明:在菱形ABCD中
OC=AC,AC⊥BD,
∵DE=AC,
∴DE=OC,
∵DE∥OC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴□OCED是矩形,
∴OE=CD.
(2) 在菱形ABCD中,AB=BC=4,
∵∠ABC=60 ,
∴△ABC是等边三角形,
∴AC=AB=4,OA=AC=2,
在Rt△AOB中,,
∵四边形OCED是矩形,
∴OD=CE=OB=,
在Rt△ACE中,.
23.(1)四边形是正方形,
,
又,
,
在和中,
,
,
,
,
;
(2)由(1)知,
,
,
又,
,
.
24.解:(1)∵四边形ABCD为矩形,四边形HEFG为菱形,
∴∠D=∠A=90°,HG=HE,又AH=DG=2,
∴Rt△AHE≌Rt△DGH(HL),
∴∠DHG=∠HEA,
∵∠AHE+∠HEA=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形HEFG为正方形;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,
∵AB//CD,
∴∠AEG=∠MGE,
∵HE//GF,
∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG,
∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,
因此S△FCG=×FM×GC=×2×(7 6)=1.
25.
解:(1)正方形,等腰直角三角形,
,
,
即、、三点共线,
,,
四边形是平行四边形,
,
故答案为:平行.
(2)①的面积是,
故答案为:8.
②的面积是:
,
故答案为:8.
③与②求法类似:的面积是
,
故答案为:8.
(3)面积与正方形的面积之间关系是S正方形ABCD.
证明:,
S正方形ABCD,
∴S正方形ABCD.
26.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E、F分别为BC、AD中点,
∴AF=AD,BE=BC,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AD=2AB,AD=2AF,
∴AB=AF,
∴四边形ABEF是菱形;
(2)①连接AE交BF于点O,
∵四边形ABEF是菱形,
∴AE⊥BF,OB=OF=BE=4,OA=OE=AE,
∴∠AOB=90°,
在Rt△AOB中,OA==3,
∴AE=2OA=6,
∴S菱形ABEF=AE·BF=×6×8=24,
∵E、F分别是BC、AD中点,
∴BE=EC,AF=FD,
∵AD∥BC,
∴四边形ABEF,四边形EFDC都是平行四边形,且底和高相等,
∴S四边形ABEF=S四边形EFDC=24,
∴S四边形ABCD=S四边形ABEF+S四边形EFDC=48,
∵CG⊥AB,
∴S四边形ABEF=AB·CG=5CG=48,∠BGC=90°,
∴CG=,
∵AD=BC=2AB=10,
∴BG=,
∴AG=AB-BG=5-=,
∵四边形ABCD是平行四边形,
∴AB=CD=5,AB∥CD,
∴∠A=∠FDH,∠GCH=∠BGC=90°,
∵F是AD中点,
∴AF=DF,
在△AFG和△DFH中,
,
∴△AFG≌△DFH(ASA),
∴AG=DH=,
∴CH=CD+DH=5+=,
在Rt△GCH中,GH==12;
②过F作FK⊥AB交BA延长线于K,
∴S四边形ABEF=AB·FK=5FK=24,
∴FK=,
∴S△BGF=BG·FK==,
S△BGC=BG·CG==,
∵S2=S△BGC-S△BGP=-S△BGP,
S1=S△BGF-S△BGP=-S△BGP,
∴S2-S1=-=.
27.(1)证明:∵点E是正方形对角线上的点,
∴,,,
∴,
∴;
(2)证明:如图,作,
∴,
∵点E是正方形对角线上的点,
∴,
∵,
∴,
在和中,,
∴,
∴.
∴矩形是正方形;
(3)解:的值是定值,定值为4.
理由:∵四边形、都是正方形,
∴,
∵,
∴,
∴,
∴.
∴.
一、单选题
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别相等 B.两组对边分别平行
C.两条对角线相等 D.两条对角线互相垂直
2.如图,在菱形中,对角线,相交于点,若,则的度数为( )
A. B. C. D.
3.下列四个命题中,真命题是( )
A.对角线垂直且相等的四边形是菱形
B.对角线互相垂直平分的四边形是正方形
C.一组邻边相等的平行四边形是正方形
D.对角线相等且互相平分的四边形是矩形
4.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )
A. B. C.9 D.12
5.如图,E是矩形的边上一点,,则等于( )
A. B. C. D.
6.如图,在正方形 中, 是 上的一点,且 ,则 的度数是()
A.20° B.22.5° C.30° D.45°
7.如图,菱形的对角线相交于点O,过点D作于点H,连接,若,,则的长( )
A. B. C. D.
8.如图所示,在矩形中,,,将矩形沿折叠,点落在点处,与交于点,则重叠部分的面积是( )
A.20 B.16 C.12 D.10
9.如图,两张等宽的纸条交叉叠放在一起,重合部分构成一个四边形,在其中一张纸条转动的过程中,下列结论一定成立的是( )
A. B.四边形面积不变
C. D.四边形周长不变
10.如图,已知四边形为正方形,,为对角线上一点,连接,过点作,交的延长线于点,以,为邻边作矩形,连接.下列结论:①矩形是正方形;②;③平分;④.其中结论正确的序号有( )
A.①③ B.②④ C.①②③ D.①②③④
二、填空题
11.菱形的对角线之比为3:4,且面积为24,则它的周长为__________.
12.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_______ (只填写序号).
13.如图,矩形的对角线相交于点O,,.若,则四边形的周长是______.
14.如图,在菱形中,对角线相交于点O,,E是线段上一点,且,则的度数是______.
15.如图,在菱形中,E,F,G分别是,,的中点,且,,则菱形的面积是___.
16.如图,在正方形ABCD中,AB=3,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为__.
17.如图,正方形的边长为,点为边上一点,,点为的中点,过点作直线分别与,相交于点,.若,则长为______.
18.如图,矩形ABCD中,AD=6,DC=8,点H在边AD上,AH=2,E为边AB上一个动点,连接HE.以HE为一边在HE的右上方作菱形HEFG,使点G落在边DC上,连接CF.
(1)当菱形HEFG为正方形时,DG的长为___;
(2)在点E的运动过程中,△FCG的面积S的取值范围为___.
三、解答题
19.如图,在菱形中,对角线与相交于点O,过点D作交的延长线于E.
(1)求证:;
(2)若,,求的周长.
20.如图,在中,点,分别是线段,的中点,且,延长至点使得,连结和.
(1)求证:四边形是矩形.
(2)若,,求的长.
21.如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E,F连接AF,CE.
(1)求证:OE=OF;
(2)求证:四边形AFCE是菱形.
22.如图,菱形ABCD的对角线AC,BD相交于点,过点D作,且,连接,连接交于点.
(1)求证:;
(2)若菱形ABCD的边长为4,,求的长.
23.如图,正方形中,点分别在边上,且,连接相交于点,作,垂足是.
(1)求证:;
(2)求证:.
24.已知,如图,矩形中,,,菱形的三个顶点,,分别在矩形的边,,上,,连接.
(1)若,求证四边形为正方形;
(2)若,求的面积.
25.已知正方形的边长为4,E是上一个动点,以点E为直角顶点,在正方形外侧等腰直角三角形,连结、、.
(1)与的位置关系是__________.
(2)①如图1,当(即点E与点D重合)时,的面积为_________.
②如图2,当(即点E为的中点)时,的面积为________.
③如图3,当时,的面积为_______.
(3)如图4,根据上述计算的结果,当E是上任意一点时,请提出你对面积与正方形的面积之间关系的猜想,并证明你的猜想.
26.如图,在平行四边形 ABCD中,,E,F分别为,的中点,作于点G,的延长线交的延长线于点H.
(1)求证:四边形是菱形.
(2)当时,
①求的长.
②如图2,交于点P,记的面积为,的面积为,则的值为________.
27.如图,已知四边形是正方形,,点E为对角线上一动点,连接.过点E作,交射线点F,以为邻边作矩形.连接.
(1)连接,求证:.
(2)求证:矩形是正方形.
(3)探究:的值是否为定值?若是,请求出这个定值,若不是,请说明理由.
答案
一、单选题
1.C
【分析】分别根据矩形和菱形的性质可得出其对角线性质的不同,可得到答案.
【解析】解:矩形的对角线相等且平分,菱形的对角线垂直且平分,
所以矩形具有而菱形不具有的为对角线相等,
故选:C.
2.B
【分析】根据菱形的性质得到,,再进一步求解即可.
【解析】解:四边形是菱形,
,,
,
,
,
故选B.
3.D
【分析】根据菱形、矩形、正方形的判定定理等知识逐项判定即可.
【解析】解:选项,对角线相等且互相垂直的四边形是菱形,若对角线不互相平分,则不是菱形,故原命题为假命题;
选项,对角线互相平分说明是平行四边形,菱形的判定定理:对角线垂直的平行四边形是菱形,故原命题为假命题;
选项,有一组邻边相等的平行四边形是菱形,故原命题为假命题;
选项,对角线相等且互相平分的四边形是矩形,为真命题;
故选:.
4.B
【分析】根据矩形对角线相等且互相平分的性质和题中的条件易得△AOB为等边三角形,即可得到矩形对角线的长,进而求解即可.
【解析】
如图:AB=6,∠AOB=60°,
∵四边形是矩形,AC,BD是对角线,
∴OA=OB=OC=OD=BD=AC,
在△AOB中,OA=OB,∠AOB=60°,
∴OA=OB=AB=6,BD=2OB=12,
∴BC=.
故选:B.
5.C
【分析】先由矩形证得,从而得,再由等腰三角形的性质求出等腰三角形的底角,再由平行线性质得出结论.
【解析】解:四边形是矩形,
∴
∴
∵,
∴
∴,
∵
∴,
故选:C
6.B
【分析】在正方形中可知∠BAC=45°,由AB=AE,进而求出∠ABE,又知∠ABE+∠EBC=90°,故能求出∠EBC.
【解析】解:在正方形ABCD中,∠BAC=45°,
∵AB=AE,
∴∠ABE=∠AEB=67.5°,
∵∠ABE+∠EBC=90°,
∴∠EBC=22.5°,
故选B.
【点睛】本题主要考查正方形的性质,等腰三角形的性质等知识点,熟练掌握基础知识是解题关键.
7.如图,菱形的对角线相交于点O,过点D作于点H,连接,若,,则的长( )
A. B. C. D.
【答案】B
【分析】根据菱形的性质得O为的中点,再由直角三角形斜边上的中线等于斜边的一半,得的长度,利用勾股定理求得的长,最后由菱形的面积公式求解.
【解析】解:∵四边形是菱形,
∴,
∵,
∴,
∴,
∵,
∴,,
∵,
∴,,
∵,即,
∴.
故选:B.
8.D
【分析】根据折叠的性质可得∠ADB=∠EDB,由平行可得∠ADB=∠CBD,推出∠CBD=∠EDB,设BF为x,在Rt△DCF中,根据勾股定理列出方程求出x,再根据面积公式求出△BDF的面积即可.
【解析】∵AD∥BC,
∴∠ADB=∠CBD,
∵△BDE是△BDA折叠后的图形,
∴∠ADB=∠EDB,
∴∠CBD=∠EDB,
设BF为x,则DF为x,CF为8-x,
在Rt△DCF中,
解得:x=5,
∴S△BDF=.
故选D.
9.A
【分析】两张等宽的纸条的宽为h,根据题意可得,从而得到四边形是平行四边形,再由,可得,进而得到四边形是菱形,即可.
【解析】解∶ 设两张等宽的纸条的宽为h,
∵纸条的对边平行,
∴,
∴四边形是平行四边形,
又∵,
∴,
∴四边形是菱形,
∴,故A选项正确,符合题意,C选项错误,不符合题意;
∵在旋转的过程中,在变化,
∴四边形面积和周长也在变化,故B、D选项错误,不符合题意;
故选:A.
10.A
【分析】过作,过作于,如图所示,根据正方形性质得,,推出四边形是正方形,由矩形性质得,,根据全等三角形的性质得,推出矩形是正方形,故①正确;根据正方形性质得,推出,得到,,由此推出平分,故③正确;进而求得,故②错误;当时,点与点重合,得到不一定等于,故④错误;故选A.
【解析】过作,过作于,如图所示,
∵四边形是正方形,
∴,,
∴,
∴,
∴四边形是正方形,
∴,
∵四边形是矩形,
∴,
∴,
在和中,
,
∴,
∴,
∴矩形是正方形,故①正确;
∴,
∵四边形是正方形
∴,
∴
在和中
∴
∴,
∵
∴平分,故③正确;
∴,故②错误;
当时,点与点重合,
∴不一定等于,故④错误.
故选:A
二、填空题
11.20
【分析】依题意,已知菱形的面积以及对角线之比,首先根据面积公式求出菱形的对角线长,然后利用勾股定理求出菱形的边长.
【解析】解:如图:
由题:,
∴可设,,
∵菱形ABCD的面积为,
∴(舍去),
∴,,
∴,,
∴中,由勾股定理得:,
∴菱形的周长是:.
故答案是:20.
12.②③或①④
【分析】要判定是正方形,则需能判定它既是菱形又是矩形.
【解析】有6种选法:(1)①②:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(2)②③:由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误;
(3)①③:由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(4)②④:由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
(5)①④:由①得有一组邻边相等的平行四边形是菱形,由④得对角线互相垂直的平行四边形是菱形,所以不能得出平行四边形ABCD是正方形,错误;
(6)③④:由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
综上所述:错误的是:②③或①④.
故答案为②③或①④.
13.40
【分析】根据矩形的对角线互相平分且相等,得到,再利用两对边平行的四边形为平行四边形得到四边形为平行四边形,利用邻边相等的平行四边形为菱形得到四边形为菱形,即可求出其周长.
【解析】∵四边形为矩形,
,,且,
∴,
,
∴四边形为平行四边形,
,
∴四边形为菱形,
.
故答案为:40
14.
【分析】由菱形的性质可得,,可得,由三角形内角和定理求得的度数,据此即可求解.
【解析】解:∵四边形是菱形,,
∴,,
∴,
∵,
∴,
∴,
故答案为:.
15.96
【分析】连接,,交点为,与交于点,与交于点,由三角形中位线定理得出,,,,得出,由勾股定理求出的长,根据菱形的面积公式可得出答案.
【解析】解:如图,连接,,交点为,与交于点,与交于点,
四边形是菱形,
,
,,分别是,,的中点,
,,,,
四边形是矩形,
,
,,
,
,,
菱形的面积是.
故答案为96.
16.4或11
【分析】根据运动过程,根据点P运动的位置和全等情况分类讨论,根据全等三角形的性质即可分别求解.
【解析】解:当点P在AB上运动时,显然A、B、P构不成三角形
∴此时不符合题意;
当点P在BC上运动时,
由AB=CD, ∠ABP=∠DCE=90°,显然此时存在△ABP≌△DCE
∴BP=CE
∴t-3=1,即t=4;
当点P在CD上运动时,如下图所示,显然不存在点P,使得△ABP和△DCE全等;
当点P在DA上运动时,如下图所示
由AB=CD, ∠A=∠DCE=90°,显然此时存在△ABP≌△CDE
∴AP=CE=1
∴3×4-t=1
解得t=11.
综上:当△ABP和△DCE全等时,t的值为4或11.
故答案为:4或11.
17.1或2
【分析】根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.
【解析】根据题意画出图形,过点作,交于点,交于点,四边形为正方形,.
在中,,cm,
cm.
根据勾股定理得cm.
为的中点,
cm,
在和中,
,
,.
PN//DC,
,
,即.
在中,,
cm.
由对称性得到 cm,
综上,等于1cm或2cm.
故答案为1或2.
18. 2
【分析】(1)由于四边形ABCD为矩形,四边形HEFG为正方形,那么∠D=∠A=∠GHE=,HG=HE,易证△GDH≌△HAE,得DG=AH=2;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于ABCD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2,进而可求△FCG的面积S的最大值和最小值,从而确定S的取值范围.
【解析】解:(1)如图1,当菱形为正方形时,,,
四边形为矩形,
,
,
,
在和中,
,
,
;
故答案为:2;
(2)如图2,过作,交延长线于,连接,
∵ABCD,
,
∵HEGF,
,
,
在和中,
,
,即无论菱形如何变化,点到直线的距离始终为定值2,
∴,
设,则,
在中,,
,
,
即,
,
,
的最小值为,此时,
的最大值为8时,,
在点的运动过程中,的面积的取值范围为:;
故答案为:;
三、解答题
19.(1)证明:四边形是菱形,
,,,
∵,
∴四边形是平行四边形,
∴,
,
.
(2)解:在菱形中,,
在中,,,
,
,
,
周长.
20.解:(1)∵E是AC中点,
∴,
∵,
∴四边形ADCF是平行四边形,
∵,
∴,
∴四边形ADCF是矩形.
(2)∵四边形ADCF是矩形,
∴,
∵D是AB中点,
∴,
∵,
∴,
∴.
21.解:(1)∵四边形ABCD是矩形,
∴AD//BC,
∴∠EAO=∠FCO,
∵AC的中点是O,
∴OA=OC,
在和中,
,
,
∴OE=OF;
(2)∵OE=OF,AO=CO,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
22.(1)证明:在菱形ABCD中
OC=AC,AC⊥BD,
∵DE=AC,
∴DE=OC,
∵DE∥OC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴□OCED是矩形,
∴OE=CD.
(2) 在菱形ABCD中,AB=BC=4,
∵∠ABC=60 ,
∴△ABC是等边三角形,
∴AC=AB=4,OA=AC=2,
在Rt△AOB中,,
∵四边形OCED是矩形,
∴OD=CE=OB=,
在Rt△ACE中,.
23.(1)四边形是正方形,
,
又,
,
在和中,
,
,
,
,
;
(2)由(1)知,
,
,
又,
,
.
24.解:(1)∵四边形ABCD为矩形,四边形HEFG为菱形,
∴∠D=∠A=90°,HG=HE,又AH=DG=2,
∴Rt△AHE≌Rt△DGH(HL),
∴∠DHG=∠HEA,
∵∠AHE+∠HEA=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形HEFG为正方形;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,
∵AB//CD,
∴∠AEG=∠MGE,
∵HE//GF,
∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG,
∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,
因此S△FCG=×FM×GC=×2×(7 6)=1.
25.
解:(1)正方形,等腰直角三角形,
,
,
即、、三点共线,
,,
四边形是平行四边形,
,
故答案为:平行.
(2)①的面积是,
故答案为:8.
②的面积是:
,
故答案为:8.
③与②求法类似:的面积是
,
故答案为:8.
(3)面积与正方形的面积之间关系是S正方形ABCD.
证明:,
S正方形ABCD,
∴S正方形ABCD.
26.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E、F分别为BC、AD中点,
∴AF=AD,BE=BC,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AD=2AB,AD=2AF,
∴AB=AF,
∴四边形ABEF是菱形;
(2)①连接AE交BF于点O,
∵四边形ABEF是菱形,
∴AE⊥BF,OB=OF=BE=4,OA=OE=AE,
∴∠AOB=90°,
在Rt△AOB中,OA==3,
∴AE=2OA=6,
∴S菱形ABEF=AE·BF=×6×8=24,
∵E、F分别是BC、AD中点,
∴BE=EC,AF=FD,
∵AD∥BC,
∴四边形ABEF,四边形EFDC都是平行四边形,且底和高相等,
∴S四边形ABEF=S四边形EFDC=24,
∴S四边形ABCD=S四边形ABEF+S四边形EFDC=48,
∵CG⊥AB,
∴S四边形ABEF=AB·CG=5CG=48,∠BGC=90°,
∴CG=,
∵AD=BC=2AB=10,
∴BG=,
∴AG=AB-BG=5-=,
∵四边形ABCD是平行四边形,
∴AB=CD=5,AB∥CD,
∴∠A=∠FDH,∠GCH=∠BGC=90°,
∵F是AD中点,
∴AF=DF,
在△AFG和△DFH中,
,
∴△AFG≌△DFH(ASA),
∴AG=DH=,
∴CH=CD+DH=5+=,
在Rt△GCH中,GH==12;
②过F作FK⊥AB交BA延长线于K,
∴S四边形ABEF=AB·FK=5FK=24,
∴FK=,
∴S△BGF=BG·FK==,
S△BGC=BG·CG==,
∵S2=S△BGC-S△BGP=-S△BGP,
S1=S△BGF-S△BGP=-S△BGP,
∴S2-S1=-=.
27.(1)证明:∵点E是正方形对角线上的点,
∴,,,
∴,
∴;
(2)证明:如图,作,
∴,
∵点E是正方形对角线上的点,
∴,
∵,
∴,
在和中,,
∴,
∴.
∴矩形是正方形;
(3)解:的值是定值,定值为4.
理由:∵四边形、都是正方形,
∴,
∵,
∴,
∴,
∴.
∴.
