沪教版八年级数学下册第20章一次函数与四边形专题试卷(含答案)
文档属性
| 名称 | 沪教版八年级数学下册第20章一次函数与四边形专题试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览




文档简介
《一次函数与四边形》
(含存在性问题、最值问题、动态问题)
一、解答题
1.在平面直角坐标系xOy中,已知直线分别与x轴、y轴交于点A、B,直线的图像与y轴交于点C,与已知直线交于点D,点D的横坐标是2
(1)求直线的解析式;
(2)将直线的图像向上或向下平移,交直线于点E,设平移所得函数图像的截距为b,如果交点E始终落在线段AB上,求b的取值范围.
(3)在x轴上是否存在点P,使点P与点A、B、C构成的四边形为梯形,如果存在,请求出点P的坐标;如果不存在,请说明理由.
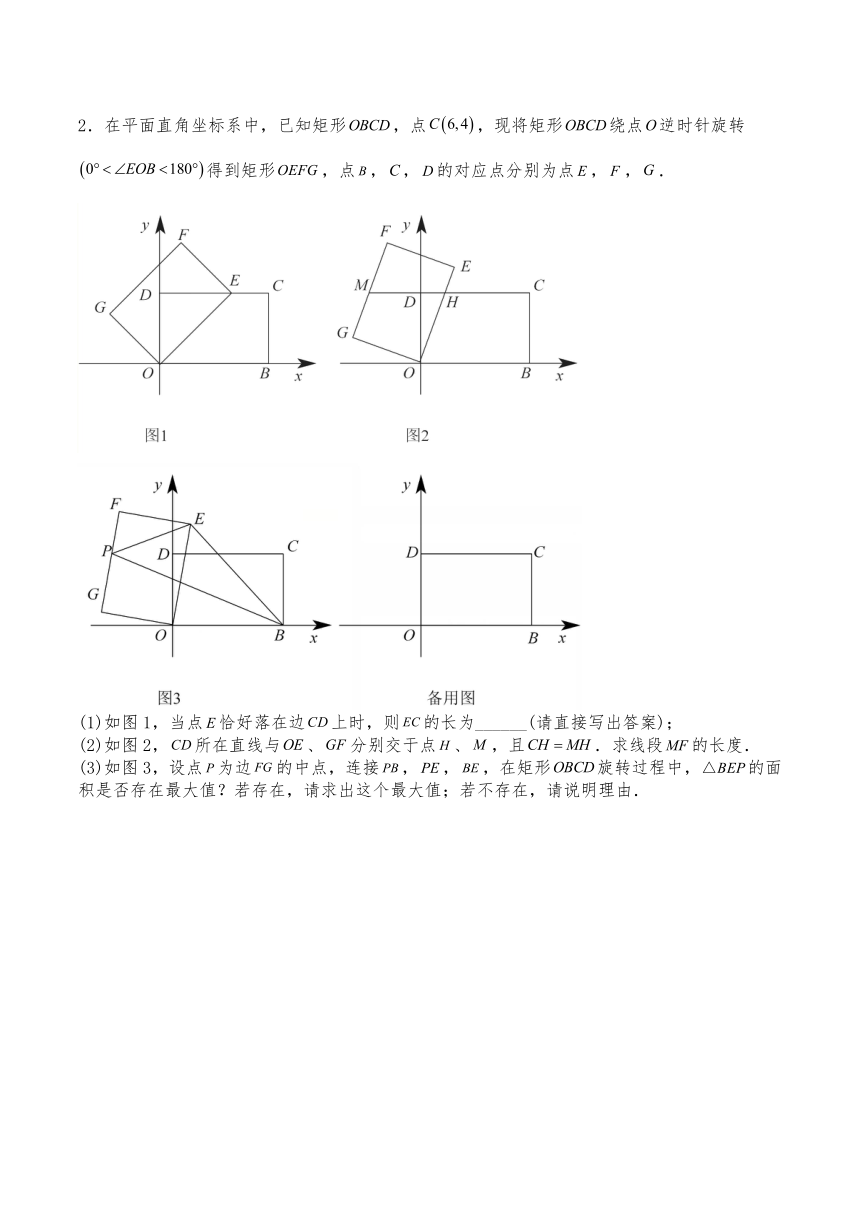
2.在平面直角坐标系中,已知矩形,点,现将矩形绕点逆时针旋转得到矩形,点,,的对应点分别为点,,.
(1)如图1,当点恰好落在边上时,则的长为______(请直接写出答案);
(2)如图2,所在直线与、分别交于点、,且.求线段的长度.
(3)如图3,设点为边的中点,连接,,,在矩形旋转过程中,的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
3.点为平面直角坐标系中的任意一点,记(分别为点的横、纵坐标),把称为点的特征数.
(1)当点的坐标为时,求的值.
(2)若点的特征数是5,点的特征数是6,求点的坐标.
(3)如图,在平面直角坐标系中,的顶点的坐标分别为、、.
点的坐标为_____.
当且点在内部(不包含边界)时,直接写出的取值范围.
当点在内部(不包含边界)时,直接写出的取值范围.
4.在平面直角坐标系中,对于两个点,和图形,如果在图形上存在点,,可以重合)使得,那么称点与点是图形的一对平衡点.
(1)如图1,已知点,.
①设点与线段上一点的距离为,则的最小值是 ,最大值是 ;
②在,,这三个点中,与点是线段的一对平衡点的是 ;
(2)如图2,已知正方形的边长为2,一边平行于轴,对角线的交点为点,点的坐标为.若点在第一象限,且点与点是正方形的一对平衡点,求的取值范围;
(3)已知点,,某正方形对角线的交点为坐标原点,边长为.若线段上的任意两个点都是此正方形的一对平衡点,直接写出的取值范围.
5.在平面直角坐标系中,点的坐标是,过点作直线轴于,作直线轴于,点、分别是直线和直线上的点,且.
(1)如图,当点、分别在线段和线段上时,求的周长;
(2)如图,当点在线段的延长线上,点在线段的延长线上时,猜想线段、和之间的数量关系,并证明你的猜想;
(3)若,直接写出的长.
6.在平面直角坐标系中,对于点P和正方形,给出如下定义:若点P关于y轴的对称点到正方形的边所在直线的最大距离是最小距离的k倍,则称点P是正方形的“k倍距离点”.已知:点A(a,0),B(a,a).
(1)当时,
①点C的坐标是 ;
②在三个点中, 是正方形的“3倍距离点”;
(2)当时,点(其中)是正方形的“2倍距离点”,求n的取值范围;
(3)点.当时,线段上存在正方形的“2倍距离点”,直接写出a的取值范围.
7.如图,在平面直角坐标系中,点A、C的坐标分别为,(4,1),以,为邻边作平行四边形,一次函数(k、b为常数,且)的图象过点B.
(1)点B的坐标为 .
(2)求用含k的代数式表示b.
(3)当一次函数的图象将平行四边形分成面积相等的两部分时,求k的值.
(4)直接写出一次函数的图象与平行四边形的边只有两个公共点时k的取值范围.
8.如图,在平面直角坐标系中,A(0,4),以OA为一边在第一象限内作矩形OABC,直线CD:交AB于点E,与y轴交于点D,.
(1)求点B的坐标.
(2)点P为线段CE上的一个动点,过点P作轴,交AB于点F,交x轴于点G,连接FD,设点p的横坐标为m,△DFP的面积为S,求S关于m的函数关系式.
(3)在(2)的条件下,连接BP并延长与x轴交于点M,过点P作,与x轴交于点,当时,在直线CD上是否存在一点R,过点作轴交直线于点Q,得,若存在,求出点R的坐标;若不存在,请说明理由.
9.已知如图,直线与两坐标轴分别交于点、,点关于轴的对称点是点,直线经过点,且与轴相交于点,点是直线上一动点,过点作轴的平行线交直线于点,再以为边向右边作正方形.
(1)①求的值;
②判断的形状,并说明理由;
(2)连接、,当的周长最短时,求点的坐标;
(3)在(2)的条件下,在轴上是否存在一点,使得是等腰三角形,若存在,请直接写出点的坐标,若不存在,请说明理由.
10.如图,平面直角坐标系中直线:分别与轴,轴交于点和点,过点的直线与轴交于点,.
(1)求直线的解析式;
(2)若为线段上一点,为线段上一点,当时,求的最小值,并求出此时点的坐标;
(3)在(2)的结论下,将沿射线方向平移得,使落在直线上,若为直线上一点,为平面内一点,当以点为顶点的四边形为菱形时,请直接写出点的坐标.
11.如图,直角三角形在平面直角坐标系中,直角边在y轴上,的长分别是一元二次方程的两个根,A,且,P为上一点,且.
(1)求点A的坐标;
(2)求过点P的反比例函数解析式;
(3)点M在第二象限内,在平面内是否存在点N,使以A,C,M,N为顶点的四边形为正方形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
12.在平面直角坐标系中,矩形,为原点,,将绕点逆时针旋转,点旋转后的对应点为.
(1)如图(1),当时,求的坐标;
(2)如图(2),当点恰好落在轴上时,与交于点.
①此时与是否相等,说明理由;
②求点的坐标;
(3)求面积的最大值.(直接写出答案即可)
13.在平面直角坐标系中,四边形是矩形,点,点,点.以点A为中心,顺时针旋转矩形,得到矩形,点O,B,C的对应点分别为D,E,F,记旋转角为.
(1)如图1,当时,求点D的坐标;
(2)如图2,当点E落在的延长线上时,求点D的坐标;
(3)当点D落在线段上时,直接写出点E的坐标.
14.如图,平面直角坐标系中,长方形的边在轴上,边在轴上,且,.
(1)在长方形的边上找一点,使得直线将长方形的面积分成1:3两部分,则点的坐标为 .
(2)如图,已知点在边上,且,请你在边上找一点,将沿翻折,使得点恰好落在轴上的点处.
求线段所在直线的函数表达式;
在线段上是否存在一点,使得直线将四边形的面积分成2:3两部分?若存在,求出符合条件的所有点坐标;若不存在,请说明理由.
15.如图,在平面直角坐标系中,点的坐标分别是,,动点从点出发,沿轴正方向以每秒个单位的速度移动,同时动点从点出发,沿射线方向以每秒个单位的速度运动.以为邻边构造,在线段延长线上取点,使,设点运动的时间为秒.
(1)当点运动到线段的中点时,求的值及点的坐标;
(2)当点在线段上时,求证:四边形为平行四边形;
(3)在线段上取点,使,过点作,截取,且点分别在第一、四象限,在运动过程中,当点中,有一点落在四边形的边上时,直接写出所有满足条件的t的值.
16.在平面直角坐标系中,如果点P的坐标为,那么把点(其中)称为点P的“位置点”.已知点.
(1)若点分别是点A,B的“位置点”,则线段 ;
(2)点M是线段上一点,点N是点M的一个“位置点”.
①当M在线段上运动时,若点M,N之间的距离的最小值为5,求k的值;
②如图,点,如果在线段上能找到至少一个点M,使点N在正方形的内部或边上,直接写出k的取值范围.
17.在平面直角坐标系中,已知点,,连接.将向下平移5个单位得线段.其中点的对应点为点,连接,.
(1)填空:点的坐标为 ,四边形的面积为 .
(2)若点是轴上的动点,连接.
①如图(1),当点在轴正半轴时,线段与线段相交于点.用等式表示三角形的面积与三角形的面积之间的关系,并说明理由;
②当将四边形的面积分成两部分时,直接写出点的坐标.
18.如图,平面直角坐标系中,矩形的对角线,
(1)求B、C两点的坐标;
(2)把矩形沿直线DE对折使点C落在点A处,与相交于点F,求四边形的面积;
(3)若点M在直线上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
19.如图,在平面直角坐标系中,边长为的正方形的边落在轴的正半轴上,边落在轴的正半轴上,点从点出发以每秒个单位长度的速度沿着射线的方向运动,点关于的对称点为点.运动时间为秒,连接,,,.
(1)如图,当时,求的度数.
(2)如图,当时,求证:.
(3)如图,过点作,且,连接,为的中点.连接,则当____时,有最小值,的最小值为_____.
20.如图,在平面直角坐标系中,直线与直线相交于点,直线与y轴交于点.
(1)求直线的函数解析式;
(2)将沿直线翻折得到,使点O与点C重合,与x轴交于点D.求证:;
(3)在直线下方是否存在点P,使为等腰直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由.
21.如图1,在平面直角坐标系中,直线与y轴交于点A,过的直线与直线交于点.
(1)求直线的解析式;
(2)若点D是第一象限位于直线上的一动点,过点D作轴交于点H.当时,试在x轴上找一点E,在直线上找一点F,使得的周长最小,求出周长的最小值;
(3)如图2,直线与x轴交于点M,与y轴交于点N,将直线绕点O逆时针旋转得到直线,点P是直线上一点,且横坐标为.在平面内是否存在一点Q,使得以点M,C,P,Q为项点的四边形是平行四边形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
22.正方形的边长为4,,交于点E.在点A处建立平面直角坐标系如图所示.
(1)如图(1),双曲线过点E,完成填空:点C的坐标是___________.点E的坐标是___________,双曲线的解析式是___________;
(2)如图(2),双曲线与,分别交于点M,N(反比例图像不一定过点E).求证;
(3)如图(3),将正方形向右平移个单位长度,使过点E的双曲线与交于点P.当是以为腰的等腰三角形时,求m的值.
23.如图,在平面直角坐标系中,于点,且点在的正半轴上,点和点分别在的负半轴和正半轴,,.
(1)求点的坐标;
(2)点点出发以1个单位/秒的速度向的负半轴方向运动,同时点从点出发向轴的正方向运动,连接交直线于点.设、两点运动时间为秒,若,连接,的面积为,请用的式子表示,并直接写出的式子表示,并直接写出的取值范围;
(3)在(2)的条件下,过点作,过点作轴的平行线交于于点,连接,是否存在,使的面积等于面积的2倍,如果存在,请求出的值,如果不存在,请说明理由.
24.如图,正方形的顶点在平面直角坐标系的原点处,,,其中点坐标为.
(1)求出点的坐标;
(2)在轴上有一点,连接,若,求的面积;
(3)在正方形的边上有一点,连接,将四边形沿所在直线翻折,当点刚好落在轴上时,求此时的长度.
25.如图,点为长方形的中心,轴,轴,,.
(1)直接写出、的坐标;
(2)如图,若点从点出发以每秒个单位长度向方向匀速移动不超过点,点从点出发以每秒个单位长度向方向匀速移动不超过点,连接、,在点、移动过程中,四边形的面积是否发生变化?若不变,求其值;若变化,求其变化范围.
(3)如图,若矩形中,,,,在轴上,矩形以每秒个单位长度向右平移秒得到矩形,点、、、分别为、、、的对应点,与此同时,点从点出发,沿矩形的边以每秒个单位长度的速度顺时针方向运动即连接,,点为的中点,当的面积为时,请直接写出的值及对应的点坐标.
26.如图,在平面直角坐标系中,直线l经过点,且平行于y轴;给出如下定义:点先关于轴对称得点,再将点关于直线对称得点,则称点是点关于轴和直线的二次反射点.
(1)已知,则它们关于轴和直线的二次反射点的坐标分别是__________________;
(2)若点的坐标是,其中,点关于轴和直线的的二次反射点是点,求线段的长;
(3)已知点,点,以线段为边在轴上方作正方形,若点关于轴和直线的二次反射点分别为,且线段与正方形的边有公共点,直接写出的取值范围.
27.如图,在平面直角坐标系中,点O是坐标原点,四边形是菱形,点A的坐标为,点C在x轴的正半轴上,直线交y轴于点M,边交y轴于点H,连接.
(1)填空:菱形的边长______;
(2)求直线的解析式;
(3)动点P从点A出发,沿折线方向以3个单位/秒的速度向终点C匀速运动,设的面积为,点P的运动时间为t秒,
①当时,求S与t之间的函数关系式;
②在点P运动过程中,当,请直接写出t的值.
28.如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时点P的坐标?
29.如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A、B两点过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
(1)求直线AM的解析式.
(2)试在直线AM上找一点P,使得,请求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是直角梯形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
答案
一、解答题
1.解:(1)直线的图象与已知直线交于点,的横坐标是2,
当时,,
的坐标为,
将的坐标代入到直线得,,
直线的解析式为;
(2)令,则,
令,则,
,
直线分别与轴、轴交于点、,
的坐标为,的坐标为,
设直线经过平移后的解析式为,如图1,
当直线经过点时,,
当直线经过点时,,
由图可得,当交点始终落在线段上时,;
(3)直线的图象与轴交于点,
时,,
的坐标为,
①如图2,当时,四边形为梯形,
直线的解析式为,
令,则,
,
②如图3,当时,四边形为梯形,
设直线的解析式为,代入点得,
直线的解析式为,
,
直线的解析式为,
令,则,
,
所以存在这样的点,使点与点、、构成的四边形为梯形,坐标为或.
2.(1)解:∵四边形.点,),
,,,
矩形是由矩形旋转得到,
,
在中,,
;
故答案为:.
(2)如图,过点作于,过点作于,连接,
,,
四边形是矩形,
,
,,,
(),
,
又,
(),
,,
又,
点与点重合,
,,
,
点,点,点三点共线,
,
,
,
设
在中,,
,
,
,
,
,,
;
(3)解:依题意,,
,,
,
当边上的高最大时,面积最大,
如图,当轴于点时,则,此时面积最大,
连接,
,
的面积的最大值为.
3.(1)解:点坐标为,
,
;
(2)解:点的特征数是5,点的特征数是6,
,
解得,
点的坐标为;
(3)解:,,
的中点为,
设,
,
解得:,
,
故答案为:;
,
,
,
设直线的解析式为,
,
解得,
直线的解析式为,
联立方程组,
解得,
直线与直线的交点为,
同理可求得直线的解析式为,
联立方程组,
解得,
直线与直线的交点为,
在内部(不包含边界)时,的取值范围为;
,
,
当直线经过点时,,
当直线经过点时,,
当,点在内部(不包含边界).
4.(1)解:①由题意知:,,则的最小值是3,最大值是;
②如图1,过作于,
,
根据平衡点的定义,点与点是线段的一对平衡点;
故答案为:3,,;
(2)如图2中,,,
且,均在正方形上,符合平衡点的定义,
;
(3)如图2,正方形边长为2,
,上任意两点关于是一对平衡点,且,的交点是,
则,,
,
,
.
5.(1)解:如图,在线段的延长线上取一点D,使,连接.
点的坐标是,直线轴于,直线轴于,
,,
四边形是边长为4的正方形,
,
在和中,
,
,
,.
,,
,
,
在和中,
,
,
.
,
即的周长是8;
(2)解:,理由如下:
如图,在线段上取一点E,使,连接.
在和中,
,
,
,.
,,
,
,
在和中,
,
,
.
;
(3)解:当点在线段上时,如图:
,
,
由(1)知的周长是8,
,
在中,,
,
解得,
;
当点在线段的延长线上时,如图:
同(2)可证,
,
,
,
在中,,
,
解得,
,
综上,的长为或.
6.(1)解:①当时,如图1,点A(4,0),B(4,4).
∵四边形是正方形,
∴,
点C的坐标是(0,4),
故答案为:(0,4);
②∵点关于y轴的对称点坐标为(1,1),
而点(1,1)到正方形的边所在直线的最大距离是,到的最小距离为1,
∴点是正方形的“3倍距离点”;
同理可得点是正方形的“1倍距离点”;
同理可得点是正方形OABC的“3倍距离点”;
∴是正方形的“3倍距离点”,
故答案为:;
(2)当时,如图2,点A(6,0),B(6,6),C(0,6),
∵点关于y轴的对称点坐标为(2,n),,
当时,到的距离倍的到的距离,
当时,到的距离倍的到的距离,
当时,到的距离倍的到的距离,
当时,到的距离倍的到的距离,
∴,
∴,
综上所述:点(其中)是正方形的“2倍距离点”时,n的取值范围是或;
(3)解:∵点关于y轴的对称点坐标为,设直线的解析式为,
代入得,
,解得:,
∴直线的解析式为,
设线段上一点P(m,m),
则,
当P在正方形内时,
①,
∴,
∴(舍去);
②,
∴,
∴;
当P在正方形外时,
,
∴,
∴;
此时不存在的情况,
∴线段上存在正方形的“2倍距离点”,a的取值范围是或.
7.(1)解:∵四边形是平行四边形,
∴,,
∴可由平移得到,
∵点,点,,
∴,
即,
故答案为:;
(2)解:将代入,得:,
∴;
(3)解:一次函数(k、b为常数,且)的图象过点B,
∴当一次函数的图象将平行四边形分成面积相等的两部分时,图象必过点,
由(2)知:,
∴,
∴;
(4)当直线经过点时,得,
解得:,
当直线经过点时,得,
解得:,
∵一次函数的图象与平行四边形的边只有两个公共点,
∴或.
8.(1)解:由题意知,,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴直线,
当时,,
∴,
∴.
(2)解:如图所示,
∵,F(m,4),
∴,
∴;
(3)解:如图2所示:
由题意可知:,
整理得:,
解得或(舍去),
∴,
∵,,,
∴,
∴,,
∴,
∵直线解析式为:,
∵,
∴直线的解析式为:,
∴,
当点再点上方时,设,
则,
∵,
∴,
∴,
∴,
根据对称性可知,也满足条件,
∴或.
9.(1)解:①令,则,
,
直线经过点,
;
②是等边三角形,理由如下:
令,则,
解得,
,
点关于轴的对称点是点,
,
,,,
是等边三角形;
(2)解:,
直线,
令,则,
,
设点关于直线的对称点为,
,
,
,
,
,
连接,则与直线的交点为点,
,
的周长,
当、、三点共线时,的周长最小,
设直线的解析式为,
,
解得,
,
联立方程组,
解得,
,
轴,
,
,
四边形是正方形,
;
(3)解:在轴上存在一点,使得是等腰三角形,理由如下:
设,
,,,
当时,,
解得或,
或;
当时,,
解得,
;
当时,,
解得或舍,
;
综上所述:点坐标为或或或.
10.(1)解:在中,令,得,
,
令,得,
,
,
,
设直线的解析式为,将,代入得,
,解得,
直线的解析式为;
(2)解:由可得,
,
,
设点是轴上一点,且满足,
,
,
过点作直线的平行线,与直线的交点就是点,
记直线的解析式为,将代入可得,
直线的解析式为,
联立,解得,
则,显然点为的中点,
如图,作点关于轴的对称点,则,作直线,则直线的解析式为:,
过点作于点,交轴于点,点即为所求,
易得直线的解析式为:,则;
(3)Ⅰ.如图,当为菱形的一条边时,
时,如图所示,过点作轴于点,
根据题意可得,,则,
则,
易得,则,
由,可得,
在Rt中,,,
,
,
同理可得,;
时,如图所示,
根据题意可得,,轴,
;
Ⅱ.如图,当为菱形的一条对角线时,
根据题意可得,,轴,
又,
可得;
综上,当以点为顶点的四边形为菱形时,的坐标分别为:,,,.
11.(1),
,
,.
∵,
∴.
∴.
(2)∵,
∴.
∴点P的坐标为.
设过点P的反比例函数解析式为.将点代入,得.
∴过点P的反比例函数解析式为.
(3)存在.
如图1,当为正方形的对角线时,
过点M作交的延长线于点E,过点C作交直线于点F.
∵四边形是正方形,
∴.
∵,
∴.
∵,
∴,
∴.
,
∴.
设,则,
∴.
∵,
∴,
∴,
∴,(舍去),
∴,
∴.
∵把先向右平移7个单位,再向上平移1个单位得,
∴把先向右平移7个单位,再向上平移1个单位得;
如图2,当为正方形的边时,
过点N作于点H,
∵四边形是正方形,
∴.
∵,
∴.
∵,
∴,
∴,
∴,
∴;
如图3,当为正方形的边时,
由图2可知,,
∵把先向右平移6个单位,再向上平移8个单位得,
∴把先向右平移6个单位,再向上平移8个单位得;
综上可知,点N的坐标为:,,.
12.(1)如图①中,过点作于点.
四边形是矩形,,
,,
在中,,,
,,
,
∴;
(2)①结论:.
理由:,,
,
,
,
,
;
②,,
,
设,
在中,,
,
,
,
.
(3)如图③中,当点值的延长线上时,此时点到的距离最大,即的面积最大.
的面积的最大值.
13.(1)解:过点作轴于,如图所示:
∵点,点,
∴,,
∵以点为中心,顺时针旋转矩形,得到矩形,
∴,,,
在Rt中,,,
∴,
∴点的坐标为;
(2)过点作轴于,,于,如图所示:
则,,
∵,,
∴,
∵,
∴,
∴,,
∴点的坐标为;
(3)连接,作轴于,如图所示:
由旋转的性质得:,,
∴,
∴,
∴,
∴,
∴,
在和中,
,
∴(),
∴,,
∴,
∴点的坐标为.
14.(1)解:,
,
,
点在上,
设,
,
直线将长方形的面积分成1:3两部分,
或,
解得或(舍),
,
故答案为:;
(2)解:,
,
过点作轴交于点,
由折叠可知,
,
,
,
,
,
在Rt 中,,
解得,
点与点重合,
,
设直线的解析式为,
,
解得,
;
存在一点,使得直线将四边形的面积分成2:3,理由如下:
设 ,
,
,
,
,
,
或,
解得或,
或.
15.(1)解:,
则 , ,
则,
则的坐标是;
(2)解:连接,如图所示:
∵四边形是平行四边形,
∴,,
∵,
∴,
即:
∴四边形是平行四边形;
(3)解:的坐标是,的坐标是,则的坐标是,的坐标是,的坐标是.
设的解析式是,
则,
解得:,
则的解析式是,
同理的解析式是,
当在上时,的坐标是,,
则 ,
解得:;
当在上时,的坐标是,
则 ,
解得:,
综合可得: ,.
16.(1)解:由题意,
∴
故答案为:8
(2)解:①点M,N之间的距离的最小时,点M,N在y轴上,此时,
∴;
②如图,当点M与A重合时,连接,延长交于点N,交于点.
观察图像 可知,
当N是M的K位置时,,
当是M的K位置时,,
观察图像 可知.
17.(1)点,将向下平移5个单位得线段,
,
即,
由平移得,,四边形是矩形,
,,
,
.
故答案为:,20;
(2)①,理由如下:
如图1,过点作于,
由平移知,轴,
,
,
由平移知,,
,,
,
即;
②如图2,当交线段于,且将四边形分成面积为两部分时,
连接,延长交轴于点,则,
,
连接,则,
将四边形的面积分成两部分,
,
由①知,,
,
,
,
,
.
(Ⅱ)如图3,当交于点,将四边形分成面积为两部分时,
连接,延长交轴于点,则,
.
连接,则,
将四边形的面积分成两部分,
,
,
.
过点作交的延长线于点,
,
,
,
,
,
,
,
,
即:点坐标为或.
18.(1),,
由勾股定理得:
∴,;
(2)由折叠的性质得:,
四边形是矩形
四边形是平行四边形
设,则
∵在中,
∴
解得:
(3)若以为边,如图
∵F是中点
由(1)知,
∴
设直线的解析式为
把点与点的坐标分别代入得:
解得:
∴直线解析式
∵四边形是菱形
∴
∴的解析式
设
∴
解得:
∴
若为边,为对角线,如图
∵四边形是平行四边形,
∴四边形是菱形
∴
∴
∴
∴
∴
∴
∴是的垂直平分线
∵四边形是菱形
∴是的垂直平分线
∴M与D重合,即
设
∵与互相平分
∴
∴,
∴
若为边,为对角线
如图
∵直线解析式
∴直线与y轴的交点为
∵,
∴
∵四边形是菱形,
∴
∴M是直线与y轴的交点
∵四边形是菱形,
∴,且
∴
综上所述,,
19.(1)解:如图,连接,
由翻折的性质可知:,,
,
是等边三角形,
,,
四边形是正方形,
,,
,
,
,
,
∴;
(2)证明:如图,作于,交于,
由翻折的性质可知:,,
设,.
,
四边形是矩形,
,,,
在中,由勾股定理得,即,
在中,由勾股定理得,即,
解得,
,
,,
,
,即;
(3)解:如图3,在的延长线上截取,连接,,,,
∵,,
∴,,
∴
,
∵,
∴,
∴,
∴,
在和中,,
∴,
∴,
∵,,
∴,
∴当点M落在线段上时,最小,最小值为(如图4中,连接),
此时,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
故答案为:,.
20.(1)解:直线与直线相交于点,
,
解得,
,
将,代入,得:
,
解得,
直线的函数解析式为;
(2)解:,,
,,
,
.
沿直线翻折得到,
,
,
;
(3)解:如图,过C作于M,
,,
,
.
由折叠的性质可知,
,
,
.
过点作,,过点作,,连接,,,与交于,
则四边形是正方形,
,,均为等腰直角三角形.
作轴于N,
,
,,
,
又,,
,
,,
,
;
四边形是正方形,
是的中点,也是的中点,
,,
的横坐标为,纵坐标为,
,
,
的横坐标为,纵坐标为,
,
综上,点P的坐标为:,,.
21.(1)解:把点代入,得:
,
∴,
∴,
设直线的解析式为∶,
把,代入得:
∴,解得:,
∴直线的解析式为;
(2)解∶如图,
设点D的坐标为,
∵轴,
∴点,
∵,
∴,解得:,
∴,,
作点D关于x轴的对称点,关于的对称点,连接,交x轴于E,交于F,则,,的周长最小,最小值为∶ ,
∵直线由直线沿y轴向上平移1个单位得到的,且直线为第一三象限的角平分线,
∴直线与坐标的夹角都为,
∴,
∴,
∵轴,
∴点的横坐标为,
∴点的坐标为,
∴,
∴的周长最小值为∶;
(3)如图,
∵点,
∴点M和点N旋转后的对应点,
∴直线的解析式为∶,
当时,,
∴,
当时,
∵,
∴,
当时,
∵,
∴,
当时,
∵,,
∴,
综上所述∶点或或.
22.(1)解:∵正方形的边长为4,,交于点E,
∴,
将E点坐标代入双曲线,
得,
解得,
∴双曲线的解析式为,
故答案为:,;
(2)∵双曲线与,分别交于点M,N,
∴设,
∴,
∴,
∴,
由正方形可知,,
∴,
∴,
∴;
(3)解:∵正方形边长为4,
由(1)知,
∴,
∵AE为腰,分两种情况:
①当 时,
∵,,点P、E在反比例数图象上,
,
∴,
②当时,点P与点B重合,
∵,点P、E在反比例数图象上,
∴,
∴;
综上所述,满足条件的m的值为2或.
23.(1)解:∵,,
∴,
∵,,
∴.
∵,
∴,
∵点C在y的正半轴上,
∴;
(2)解:如图,连接,
∵,
∴,
∵,,
∴,
∴,
∴,即是斜边的中线,
过点D作轴交直线于点H,
∵轴,,.
∴,, ,
∴,
在和中,
,
∴,
∴,
∴D,G两点速度相同,
当时,如图1,
∵,
∴,
∴,
当时,D点与O点重合,此时,
如图2,当时,
∵,
∴;
故 .
(3)解:如图3,
连接、、,过点F作于点E,过点P作交x轴于点I,
∴为等腰直角三角形,且,
∴点,.
过点F作交于点M,
则四边形为正方形,
由(2)可得,
∴,
∴,
∵四边形为正方形,
∴
当时,,
∴,
解得,
当时,,
∴,
解得.
∴存在t,使的面积等于面积的2倍,或.
24.(1)解:作轴交轴于点,轴交轴于点,轴交轴于,交于,延长交轴于,
轴,
,
,
在和中,
,
,
,
点坐标为,
,
点坐标为,
同理可得,
,
,
,
四边形为矩形,
,
,
点坐标为,
点坐标为,点坐标为;
(2)解:设点的坐标为,
由(1)得,点坐标为,点坐标为,
,
,
解得,
点的坐标为,
作轴交轴于点,轴交轴于点,
点坐标为,点坐标为,点的坐标为,
则,
,
的面积为;
(3)解:要使四边形沿所在直线翻折,当点刚好落在轴上,则轴,画出图如图所示,
与轴的交点为点,与轴的交点为点,
,,
,
在和中,
,
(AAS),
,
设,则,
,
,
解得,
为的长,
,
的长为.
25.(1)解:,,
,;
(2)四边形的面积不发生变化,理由如下:
由题可知,,,
,
,
,
,
,
四边形的面积不发生变化;
(3),△的面积为12,
点到的距离是6,
,
,,
当时,在轴的左侧,
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得;
,,,,
是的中点,
,;
当时,在轴的右侧,
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得;
,,,,
是的中点,
,;
综上所述:点坐标为,或,.
26.(1)解:∵
∴点关于轴对称点的坐标为,
∵关于直线对称的点
∴关于轴和直线的二次反射点的坐标
∵
∴点关于轴对称点的坐标为,
∵关于直线对称的点
∴关于轴和直线的二次反射点的坐标
∵
∴点关于轴对称点的坐标为,
∵关于直线对称的点
∴关于轴和直线的二次反射点的坐标
故答案为:、、
(2)∵点的坐标是,
∴点关于轴对称点的坐标为,
∴关于直线对称的点,
∴;
(3)∵点
∴点关于轴和直线的二次反射点分别为,
当与有公共点时,
,
解得
当与有公共点时,
解得
综上:或
27.(1)解:∵点A的坐标为,
∴
在中,,
故答案为:5;
(2)解:∵四边形是菱形,
∴,即.
设直线的解析式,函数图象过点,
则,
解得,
∴直线的解析式为:;
(3)解:由,令,,则,则,
①当时,如图所示,
,,
∴,
∴,
②设M到直线的距离为h,
∴
则,
解得,
当时,如图所示,
,,
,
当时,代入,
解得,
代入,
解得,
综上所述或.
28.(1)
解:点坐标为,,
,
梯形的周长为:,
根据PD将梯形COAB的周长平分,
由,
得.
此时点在上;
(2)
解:作于,于,于,
则.
,
,
,
,
,.
;
(3)
解:点只能在或上,
(ⅰ)当点在上时,设点的坐标为.
由,
得,得,
此时.
由,得.
即在7秒时有点(,);
(ⅱ)当点在上时,设点的坐标为.
由,
得,得,
此时.
即在秒时,有点(,).
故在7秒时有点(,),在秒时有点(,),使将梯形的面积分成的两部分.
29.(1)
解:∵交x轴于A,
∴,解得,
∴,
∵交y轴于B,
∴当x=0时,
∴,
∵M为OB中点,
∴,
设过,,
得到,解得,
∴直线AM的解析式是.
(2)
解:过O作直线,为与AM交点,如图1,
∴ 点P1到直线AB的距离等于点O到直线AB的距离
∴此时,
设直线,
∵,
∴
∴,
∵直线AM的解析式是
∴,解得,
此时
∴,
由是直线AB:向下平移8个单位得到的,
把直线AB:向上平移8个单位得到
交直线AM于,此时,
∴由,得,
∴.
综上所述,点P的坐标为,
(3)
解:①过点B作BHAM,过点A作AH⊥BH于点H,如图2,
如图,则,
设直线BH的表达式为:
∵
∴
∵直线BH经过点
∴
∴直线BH的表达式为,
设直线AH的表达式为,
∵,
∴,得到,
又∵直线AH过点
∴,解得
∴直线AH的表达式为,
由 解得
∴此时点H的坐标为;
②过点A作,作BH⊥AH,垂足为点H,则,如图3,
∵,,
∴此时点H的坐标为,
③过点M作AB的平行线,分别过点A、B向AB的平行线作垂线,垂足分别为H1、H2,如图4,此时,
设直线MH1的表达式为
∵
∴
∵直线MH1经过点
∴
∴直线MH1的表达式为,
设直线AH1的表达式为
∵,
则,,
∵过点
∴
解得
∴直线AH1的表达式为
由 解得
∴,
当时,
∵为矩形,
把点经过向左平移4个单位,向上平移8个单位即可得到点H2
∴点H的坐标为,,,.
(含存在性问题、最值问题、动态问题)
一、解答题
1.在平面直角坐标系xOy中,已知直线分别与x轴、y轴交于点A、B,直线的图像与y轴交于点C,与已知直线交于点D,点D的横坐标是2
(1)求直线的解析式;
(2)将直线的图像向上或向下平移,交直线于点E,设平移所得函数图像的截距为b,如果交点E始终落在线段AB上,求b的取值范围.
(3)在x轴上是否存在点P,使点P与点A、B、C构成的四边形为梯形,如果存在,请求出点P的坐标;如果不存在,请说明理由.
2.在平面直角坐标系中,已知矩形,点,现将矩形绕点逆时针旋转得到矩形,点,,的对应点分别为点,,.
(1)如图1,当点恰好落在边上时,则的长为______(请直接写出答案);
(2)如图2,所在直线与、分别交于点、,且.求线段的长度.
(3)如图3,设点为边的中点,连接,,,在矩形旋转过程中,的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
3.点为平面直角坐标系中的任意一点,记(分别为点的横、纵坐标),把称为点的特征数.
(1)当点的坐标为时,求的值.
(2)若点的特征数是5,点的特征数是6,求点的坐标.
(3)如图,在平面直角坐标系中,的顶点的坐标分别为、、.
点的坐标为_____.
当且点在内部(不包含边界)时,直接写出的取值范围.
当点在内部(不包含边界)时,直接写出的取值范围.
4.在平面直角坐标系中,对于两个点,和图形,如果在图形上存在点,,可以重合)使得,那么称点与点是图形的一对平衡点.
(1)如图1,已知点,.
①设点与线段上一点的距离为,则的最小值是 ,最大值是 ;
②在,,这三个点中,与点是线段的一对平衡点的是 ;
(2)如图2,已知正方形的边长为2,一边平行于轴,对角线的交点为点,点的坐标为.若点在第一象限,且点与点是正方形的一对平衡点,求的取值范围;
(3)已知点,,某正方形对角线的交点为坐标原点,边长为.若线段上的任意两个点都是此正方形的一对平衡点,直接写出的取值范围.
5.在平面直角坐标系中,点的坐标是,过点作直线轴于,作直线轴于,点、分别是直线和直线上的点,且.
(1)如图,当点、分别在线段和线段上时,求的周长;
(2)如图,当点在线段的延长线上,点在线段的延长线上时,猜想线段、和之间的数量关系,并证明你的猜想;
(3)若,直接写出的长.
6.在平面直角坐标系中,对于点P和正方形,给出如下定义:若点P关于y轴的对称点到正方形的边所在直线的最大距离是最小距离的k倍,则称点P是正方形的“k倍距离点”.已知:点A(a,0),B(a,a).
(1)当时,
①点C的坐标是 ;
②在三个点中, 是正方形的“3倍距离点”;
(2)当时,点(其中)是正方形的“2倍距离点”,求n的取值范围;
(3)点.当时,线段上存在正方形的“2倍距离点”,直接写出a的取值范围.
7.如图,在平面直角坐标系中,点A、C的坐标分别为,(4,1),以,为邻边作平行四边形,一次函数(k、b为常数,且)的图象过点B.
(1)点B的坐标为 .
(2)求用含k的代数式表示b.
(3)当一次函数的图象将平行四边形分成面积相等的两部分时,求k的值.
(4)直接写出一次函数的图象与平行四边形的边只有两个公共点时k的取值范围.
8.如图,在平面直角坐标系中,A(0,4),以OA为一边在第一象限内作矩形OABC,直线CD:交AB于点E,与y轴交于点D,.
(1)求点B的坐标.
(2)点P为线段CE上的一个动点,过点P作轴,交AB于点F,交x轴于点G,连接FD,设点p的横坐标为m,△DFP的面积为S,求S关于m的函数关系式.
(3)在(2)的条件下,连接BP并延长与x轴交于点M,过点P作,与x轴交于点,当时,在直线CD上是否存在一点R,过点作轴交直线于点Q,得,若存在,求出点R的坐标;若不存在,请说明理由.
9.已知如图,直线与两坐标轴分别交于点、,点关于轴的对称点是点,直线经过点,且与轴相交于点,点是直线上一动点,过点作轴的平行线交直线于点,再以为边向右边作正方形.
(1)①求的值;
②判断的形状,并说明理由;
(2)连接、,当的周长最短时,求点的坐标;
(3)在(2)的条件下,在轴上是否存在一点,使得是等腰三角形,若存在,请直接写出点的坐标,若不存在,请说明理由.
10.如图,平面直角坐标系中直线:分别与轴,轴交于点和点,过点的直线与轴交于点,.
(1)求直线的解析式;
(2)若为线段上一点,为线段上一点,当时,求的最小值,并求出此时点的坐标;
(3)在(2)的结论下,将沿射线方向平移得,使落在直线上,若为直线上一点,为平面内一点,当以点为顶点的四边形为菱形时,请直接写出点的坐标.
11.如图,直角三角形在平面直角坐标系中,直角边在y轴上,的长分别是一元二次方程的两个根,A,且,P为上一点,且.
(1)求点A的坐标;
(2)求过点P的反比例函数解析式;
(3)点M在第二象限内,在平面内是否存在点N,使以A,C,M,N为顶点的四边形为正方形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
12.在平面直角坐标系中,矩形,为原点,,将绕点逆时针旋转,点旋转后的对应点为.
(1)如图(1),当时,求的坐标;
(2)如图(2),当点恰好落在轴上时,与交于点.
①此时与是否相等,说明理由;
②求点的坐标;
(3)求面积的最大值.(直接写出答案即可)
13.在平面直角坐标系中,四边形是矩形,点,点,点.以点A为中心,顺时针旋转矩形,得到矩形,点O,B,C的对应点分别为D,E,F,记旋转角为.
(1)如图1,当时,求点D的坐标;
(2)如图2,当点E落在的延长线上时,求点D的坐标;
(3)当点D落在线段上时,直接写出点E的坐标.
14.如图,平面直角坐标系中,长方形的边在轴上,边在轴上,且,.
(1)在长方形的边上找一点,使得直线将长方形的面积分成1:3两部分,则点的坐标为 .
(2)如图,已知点在边上,且,请你在边上找一点,将沿翻折,使得点恰好落在轴上的点处.
求线段所在直线的函数表达式;
在线段上是否存在一点,使得直线将四边形的面积分成2:3两部分?若存在,求出符合条件的所有点坐标;若不存在,请说明理由.
15.如图,在平面直角坐标系中,点的坐标分别是,,动点从点出发,沿轴正方向以每秒个单位的速度移动,同时动点从点出发,沿射线方向以每秒个单位的速度运动.以为邻边构造,在线段延长线上取点,使,设点运动的时间为秒.
(1)当点运动到线段的中点时,求的值及点的坐标;
(2)当点在线段上时,求证:四边形为平行四边形;
(3)在线段上取点,使,过点作,截取,且点分别在第一、四象限,在运动过程中,当点中,有一点落在四边形的边上时,直接写出所有满足条件的t的值.
16.在平面直角坐标系中,如果点P的坐标为,那么把点(其中)称为点P的“位置点”.已知点.
(1)若点分别是点A,B的“位置点”,则线段 ;
(2)点M是线段上一点,点N是点M的一个“位置点”.
①当M在线段上运动时,若点M,N之间的距离的最小值为5,求k的值;
②如图,点,如果在线段上能找到至少一个点M,使点N在正方形的内部或边上,直接写出k的取值范围.
17.在平面直角坐标系中,已知点,,连接.将向下平移5个单位得线段.其中点的对应点为点,连接,.
(1)填空:点的坐标为 ,四边形的面积为 .
(2)若点是轴上的动点,连接.
①如图(1),当点在轴正半轴时,线段与线段相交于点.用等式表示三角形的面积与三角形的面积之间的关系,并说明理由;
②当将四边形的面积分成两部分时,直接写出点的坐标.
18.如图,平面直角坐标系中,矩形的对角线,
(1)求B、C两点的坐标;
(2)把矩形沿直线DE对折使点C落在点A处,与相交于点F,求四边形的面积;
(3)若点M在直线上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
19.如图,在平面直角坐标系中,边长为的正方形的边落在轴的正半轴上,边落在轴的正半轴上,点从点出发以每秒个单位长度的速度沿着射线的方向运动,点关于的对称点为点.运动时间为秒,连接,,,.
(1)如图,当时,求的度数.
(2)如图,当时,求证:.
(3)如图,过点作,且,连接,为的中点.连接,则当____时,有最小值,的最小值为_____.
20.如图,在平面直角坐标系中,直线与直线相交于点,直线与y轴交于点.
(1)求直线的函数解析式;
(2)将沿直线翻折得到,使点O与点C重合,与x轴交于点D.求证:;
(3)在直线下方是否存在点P,使为等腰直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由.
21.如图1,在平面直角坐标系中,直线与y轴交于点A,过的直线与直线交于点.
(1)求直线的解析式;
(2)若点D是第一象限位于直线上的一动点,过点D作轴交于点H.当时,试在x轴上找一点E,在直线上找一点F,使得的周长最小,求出周长的最小值;
(3)如图2,直线与x轴交于点M,与y轴交于点N,将直线绕点O逆时针旋转得到直线,点P是直线上一点,且横坐标为.在平面内是否存在一点Q,使得以点M,C,P,Q为项点的四边形是平行四边形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
22.正方形的边长为4,,交于点E.在点A处建立平面直角坐标系如图所示.
(1)如图(1),双曲线过点E,完成填空:点C的坐标是___________.点E的坐标是___________,双曲线的解析式是___________;
(2)如图(2),双曲线与,分别交于点M,N(反比例图像不一定过点E).求证;
(3)如图(3),将正方形向右平移个单位长度,使过点E的双曲线与交于点P.当是以为腰的等腰三角形时,求m的值.
23.如图,在平面直角坐标系中,于点,且点在的正半轴上,点和点分别在的负半轴和正半轴,,.
(1)求点的坐标;
(2)点点出发以1个单位/秒的速度向的负半轴方向运动,同时点从点出发向轴的正方向运动,连接交直线于点.设、两点运动时间为秒,若,连接,的面积为,请用的式子表示,并直接写出的式子表示,并直接写出的取值范围;
(3)在(2)的条件下,过点作,过点作轴的平行线交于于点,连接,是否存在,使的面积等于面积的2倍,如果存在,请求出的值,如果不存在,请说明理由.
24.如图,正方形的顶点在平面直角坐标系的原点处,,,其中点坐标为.
(1)求出点的坐标;
(2)在轴上有一点,连接,若,求的面积;
(3)在正方形的边上有一点,连接,将四边形沿所在直线翻折,当点刚好落在轴上时,求此时的长度.
25.如图,点为长方形的中心,轴,轴,,.
(1)直接写出、的坐标;
(2)如图,若点从点出发以每秒个单位长度向方向匀速移动不超过点,点从点出发以每秒个单位长度向方向匀速移动不超过点,连接、,在点、移动过程中,四边形的面积是否发生变化?若不变,求其值;若变化,求其变化范围.
(3)如图,若矩形中,,,,在轴上,矩形以每秒个单位长度向右平移秒得到矩形,点、、、分别为、、、的对应点,与此同时,点从点出发,沿矩形的边以每秒个单位长度的速度顺时针方向运动即连接,,点为的中点,当的面积为时,请直接写出的值及对应的点坐标.
26.如图,在平面直角坐标系中,直线l经过点,且平行于y轴;给出如下定义:点先关于轴对称得点,再将点关于直线对称得点,则称点是点关于轴和直线的二次反射点.
(1)已知,则它们关于轴和直线的二次反射点的坐标分别是__________________;
(2)若点的坐标是,其中,点关于轴和直线的的二次反射点是点,求线段的长;
(3)已知点,点,以线段为边在轴上方作正方形,若点关于轴和直线的二次反射点分别为,且线段与正方形的边有公共点,直接写出的取值范围.
27.如图,在平面直角坐标系中,点O是坐标原点,四边形是菱形,点A的坐标为,点C在x轴的正半轴上,直线交y轴于点M,边交y轴于点H,连接.
(1)填空:菱形的边长______;
(2)求直线的解析式;
(3)动点P从点A出发,沿折线方向以3个单位/秒的速度向终点C匀速运动,设的面积为,点P的运动时间为t秒,
①当时,求S与t之间的函数关系式;
②在点P运动过程中,当,请直接写出t的值.
28.如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(1)求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上;
(2)动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围;
(3)几秒后线段PD将梯形COAB的面积分成1:3的两部分?求出此时点P的坐标?
29.如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A、B两点过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
(1)求直线AM的解析式.
(2)试在直线AM上找一点P,使得,请求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是直角梯形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
答案
一、解答题
1.解:(1)直线的图象与已知直线交于点,的横坐标是2,
当时,,
的坐标为,
将的坐标代入到直线得,,
直线的解析式为;
(2)令,则,
令,则,
,
直线分别与轴、轴交于点、,
的坐标为,的坐标为,
设直线经过平移后的解析式为,如图1,
当直线经过点时,,
当直线经过点时,,
由图可得,当交点始终落在线段上时,;
(3)直线的图象与轴交于点,
时,,
的坐标为,
①如图2,当时,四边形为梯形,
直线的解析式为,
令,则,
,
②如图3,当时,四边形为梯形,
设直线的解析式为,代入点得,
直线的解析式为,
,
直线的解析式为,
令,则,
,
所以存在这样的点,使点与点、、构成的四边形为梯形,坐标为或.
2.(1)解:∵四边形.点,),
,,,
矩形是由矩形旋转得到,
,
在中,,
;
故答案为:.
(2)如图,过点作于,过点作于,连接,
,,
四边形是矩形,
,
,,,
(),
,
又,
(),
,,
又,
点与点重合,
,,
,
点,点,点三点共线,
,
,
,
设
在中,,
,
,
,
,
,,
;
(3)解:依题意,,
,,
,
当边上的高最大时,面积最大,
如图,当轴于点时,则,此时面积最大,
连接,
,
的面积的最大值为.
3.(1)解:点坐标为,
,
;
(2)解:点的特征数是5,点的特征数是6,
,
解得,
点的坐标为;
(3)解:,,
的中点为,
设,
,
解得:,
,
故答案为:;
,
,
,
设直线的解析式为,
,
解得,
直线的解析式为,
联立方程组,
解得,
直线与直线的交点为,
同理可求得直线的解析式为,
联立方程组,
解得,
直线与直线的交点为,
在内部(不包含边界)时,的取值范围为;
,
,
当直线经过点时,,
当直线经过点时,,
当,点在内部(不包含边界).
4.(1)解:①由题意知:,,则的最小值是3,最大值是;
②如图1,过作于,
,
根据平衡点的定义,点与点是线段的一对平衡点;
故答案为:3,,;
(2)如图2中,,,
且,均在正方形上,符合平衡点的定义,
;
(3)如图2,正方形边长为2,
,上任意两点关于是一对平衡点,且,的交点是,
则,,
,
,
.
5.(1)解:如图,在线段的延长线上取一点D,使,连接.
点的坐标是,直线轴于,直线轴于,
,,
四边形是边长为4的正方形,
,
在和中,
,
,
,.
,,
,
,
在和中,
,
,
.
,
即的周长是8;
(2)解:,理由如下:
如图,在线段上取一点E,使,连接.
在和中,
,
,
,.
,,
,
,
在和中,
,
,
.
;
(3)解:当点在线段上时,如图:
,
,
由(1)知的周长是8,
,
在中,,
,
解得,
;
当点在线段的延长线上时,如图:
同(2)可证,
,
,
,
在中,,
,
解得,
,
综上,的长为或.
6.(1)解:①当时,如图1,点A(4,0),B(4,4).
∵四边形是正方形,
∴,
点C的坐标是(0,4),
故答案为:(0,4);
②∵点关于y轴的对称点坐标为(1,1),
而点(1,1)到正方形的边所在直线的最大距离是,到的最小距离为1,
∴点是正方形的“3倍距离点”;
同理可得点是正方形的“1倍距离点”;
同理可得点是正方形OABC的“3倍距离点”;
∴是正方形的“3倍距离点”,
故答案为:;
(2)当时,如图2,点A(6,0),B(6,6),C(0,6),
∵点关于y轴的对称点坐标为(2,n),,
当时,到的距离倍的到的距离,
当时,到的距离倍的到的距离,
当时,到的距离倍的到的距离,
当时,到的距离倍的到的距离,
∴,
∴,
综上所述:点(其中)是正方形的“2倍距离点”时,n的取值范围是或;
(3)解:∵点关于y轴的对称点坐标为,设直线的解析式为,
代入得,
,解得:,
∴直线的解析式为,
设线段上一点P(m,m),
则,
当P在正方形内时,
①,
∴,
∴(舍去);
②,
∴,
∴;
当P在正方形外时,
,
∴,
∴;
此时不存在的情况,
∴线段上存在正方形的“2倍距离点”,a的取值范围是或.
7.(1)解:∵四边形是平行四边形,
∴,,
∴可由平移得到,
∵点,点,,
∴,
即,
故答案为:;
(2)解:将代入,得:,
∴;
(3)解:一次函数(k、b为常数,且)的图象过点B,
∴当一次函数的图象将平行四边形分成面积相等的两部分时,图象必过点,
由(2)知:,
∴,
∴;
(4)当直线经过点时,得,
解得:,
当直线经过点时,得,
解得:,
∵一次函数的图象与平行四边形的边只有两个公共点,
∴或.
8.(1)解:由题意知,,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴直线,
当时,,
∴,
∴.
(2)解:如图所示,
∵,F(m,4),
∴,
∴;
(3)解:如图2所示:
由题意可知:,
整理得:,
解得或(舍去),
∴,
∵,,,
∴,
∴,,
∴,
∵直线解析式为:,
∵,
∴直线的解析式为:,
∴,
当点再点上方时,设,
则,
∵,
∴,
∴,
∴,
根据对称性可知,也满足条件,
∴或.
9.(1)解:①令,则,
,
直线经过点,
;
②是等边三角形,理由如下:
令,则,
解得,
,
点关于轴的对称点是点,
,
,,,
是等边三角形;
(2)解:,
直线,
令,则,
,
设点关于直线的对称点为,
,
,
,
,
,
连接,则与直线的交点为点,
,
的周长,
当、、三点共线时,的周长最小,
设直线的解析式为,
,
解得,
,
联立方程组,
解得,
,
轴,
,
,
四边形是正方形,
;
(3)解:在轴上存在一点,使得是等腰三角形,理由如下:
设,
,,,
当时,,
解得或,
或;
当时,,
解得,
;
当时,,
解得或舍,
;
综上所述:点坐标为或或或.
10.(1)解:在中,令,得,
,
令,得,
,
,
,
设直线的解析式为,将,代入得,
,解得,
直线的解析式为;
(2)解:由可得,
,
,
设点是轴上一点,且满足,
,
,
过点作直线的平行线,与直线的交点就是点,
记直线的解析式为,将代入可得,
直线的解析式为,
联立,解得,
则,显然点为的中点,
如图,作点关于轴的对称点,则,作直线,则直线的解析式为:,
过点作于点,交轴于点,点即为所求,
易得直线的解析式为:,则;
(3)Ⅰ.如图,当为菱形的一条边时,
时,如图所示,过点作轴于点,
根据题意可得,,则,
则,
易得,则,
由,可得,
在Rt中,,,
,
,
同理可得,;
时,如图所示,
根据题意可得,,轴,
;
Ⅱ.如图,当为菱形的一条对角线时,
根据题意可得,,轴,
又,
可得;
综上,当以点为顶点的四边形为菱形时,的坐标分别为:,,,.
11.(1),
,
,.
∵,
∴.
∴.
(2)∵,
∴.
∴点P的坐标为.
设过点P的反比例函数解析式为.将点代入,得.
∴过点P的反比例函数解析式为.
(3)存在.
如图1,当为正方形的对角线时,
过点M作交的延长线于点E,过点C作交直线于点F.
∵四边形是正方形,
∴.
∵,
∴.
∵,
∴,
∴.
,
∴.
设,则,
∴.
∵,
∴,
∴,
∴,(舍去),
∴,
∴.
∵把先向右平移7个单位,再向上平移1个单位得,
∴把先向右平移7个单位,再向上平移1个单位得;
如图2,当为正方形的边时,
过点N作于点H,
∵四边形是正方形,
∴.
∵,
∴.
∵,
∴,
∴,
∴,
∴;
如图3,当为正方形的边时,
由图2可知,,
∵把先向右平移6个单位,再向上平移8个单位得,
∴把先向右平移6个单位,再向上平移8个单位得;
综上可知,点N的坐标为:,,.
12.(1)如图①中,过点作于点.
四边形是矩形,,
,,
在中,,,
,,
,
∴;
(2)①结论:.
理由:,,
,
,
,
,
;
②,,
,
设,
在中,,
,
,
,
.
(3)如图③中,当点值的延长线上时,此时点到的距离最大,即的面积最大.
的面积的最大值.
13.(1)解:过点作轴于,如图所示:
∵点,点,
∴,,
∵以点为中心,顺时针旋转矩形,得到矩形,
∴,,,
在Rt中,,,
∴,
∴点的坐标为;
(2)过点作轴于,,于,如图所示:
则,,
∵,,
∴,
∵,
∴,
∴,,
∴点的坐标为;
(3)连接,作轴于,如图所示:
由旋转的性质得:,,
∴,
∴,
∴,
∴,
∴,
在和中,
,
∴(),
∴,,
∴,
∴点的坐标为.
14.(1)解:,
,
,
点在上,
设,
,
直线将长方形的面积分成1:3两部分,
或,
解得或(舍),
,
故答案为:;
(2)解:,
,
过点作轴交于点,
由折叠可知,
,
,
,
,
,
在Rt 中,,
解得,
点与点重合,
,
设直线的解析式为,
,
解得,
;
存在一点,使得直线将四边形的面积分成2:3,理由如下:
设 ,
,
,
,
,
,
或,
解得或,
或.
15.(1)解:,
则 , ,
则,
则的坐标是;
(2)解:连接,如图所示:
∵四边形是平行四边形,
∴,,
∵,
∴,
即:
∴四边形是平行四边形;
(3)解:的坐标是,的坐标是,则的坐标是,的坐标是,的坐标是.
设的解析式是,
则,
解得:,
则的解析式是,
同理的解析式是,
当在上时,的坐标是,,
则 ,
解得:;
当在上时,的坐标是,
则 ,
解得:,
综合可得: ,.
16.(1)解:由题意,
∴
故答案为:8
(2)解:①点M,N之间的距离的最小时,点M,N在y轴上,此时,
∴;
②如图,当点M与A重合时,连接,延长交于点N,交于点.
观察图像 可知,
当N是M的K位置时,,
当是M的K位置时,,
观察图像 可知.
17.(1)点,将向下平移5个单位得线段,
,
即,
由平移得,,四边形是矩形,
,,
,
.
故答案为:,20;
(2)①,理由如下:
如图1,过点作于,
由平移知,轴,
,
,
由平移知,,
,,
,
即;
②如图2,当交线段于,且将四边形分成面积为两部分时,
连接,延长交轴于点,则,
,
连接,则,
将四边形的面积分成两部分,
,
由①知,,
,
,
,
,
.
(Ⅱ)如图3,当交于点,将四边形分成面积为两部分时,
连接,延长交轴于点,则,
.
连接,则,
将四边形的面积分成两部分,
,
,
.
过点作交的延长线于点,
,
,
,
,
,
,
,
,
即:点坐标为或.
18.(1),,
由勾股定理得:
∴,;
(2)由折叠的性质得:,
四边形是矩形
四边形是平行四边形
设,则
∵在中,
∴
解得:
(3)若以为边,如图
∵F是中点
由(1)知,
∴
设直线的解析式为
把点与点的坐标分别代入得:
解得:
∴直线解析式
∵四边形是菱形
∴
∴的解析式
设
∴
解得:
∴
若为边,为对角线,如图
∵四边形是平行四边形,
∴四边形是菱形
∴
∴
∴
∴
∴
∴
∴是的垂直平分线
∵四边形是菱形
∴是的垂直平分线
∴M与D重合,即
设
∵与互相平分
∴
∴,
∴
若为边,为对角线
如图
∵直线解析式
∴直线与y轴的交点为
∵,
∴
∵四边形是菱形,
∴
∴M是直线与y轴的交点
∵四边形是菱形,
∴,且
∴
综上所述,,
19.(1)解:如图,连接,
由翻折的性质可知:,,
,
是等边三角形,
,,
四边形是正方形,
,,
,
,
,
,
∴;
(2)证明:如图,作于,交于,
由翻折的性质可知:,,
设,.
,
四边形是矩形,
,,,
在中,由勾股定理得,即,
在中,由勾股定理得,即,
解得,
,
,,
,
,即;
(3)解:如图3,在的延长线上截取,连接,,,,
∵,,
∴,,
∴
,
∵,
∴,
∴,
∴,
在和中,,
∴,
∴,
∵,,
∴,
∴当点M落在线段上时,最小,最小值为(如图4中,连接),
此时,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
故答案为:,.
20.(1)解:直线与直线相交于点,
,
解得,
,
将,代入,得:
,
解得,
直线的函数解析式为;
(2)解:,,
,,
,
.
沿直线翻折得到,
,
,
;
(3)解:如图,过C作于M,
,,
,
.
由折叠的性质可知,
,
,
.
过点作,,过点作,,连接,,,与交于,
则四边形是正方形,
,,均为等腰直角三角形.
作轴于N,
,
,,
,
又,,
,
,,
,
;
四边形是正方形,
是的中点,也是的中点,
,,
的横坐标为,纵坐标为,
,
,
的横坐标为,纵坐标为,
,
综上,点P的坐标为:,,.
21.(1)解:把点代入,得:
,
∴,
∴,
设直线的解析式为∶,
把,代入得:
∴,解得:,
∴直线的解析式为;
(2)解∶如图,
设点D的坐标为,
∵轴,
∴点,
∵,
∴,解得:,
∴,,
作点D关于x轴的对称点,关于的对称点,连接,交x轴于E,交于F,则,,的周长最小,最小值为∶ ,
∵直线由直线沿y轴向上平移1个单位得到的,且直线为第一三象限的角平分线,
∴直线与坐标的夹角都为,
∴,
∴,
∵轴,
∴点的横坐标为,
∴点的坐标为,
∴,
∴的周长最小值为∶;
(3)如图,
∵点,
∴点M和点N旋转后的对应点,
∴直线的解析式为∶,
当时,,
∴,
当时,
∵,
∴,
当时,
∵,
∴,
当时,
∵,,
∴,
综上所述∶点或或.
22.(1)解:∵正方形的边长为4,,交于点E,
∴,
将E点坐标代入双曲线,
得,
解得,
∴双曲线的解析式为,
故答案为:,;
(2)∵双曲线与,分别交于点M,N,
∴设,
∴,
∴,
∴,
由正方形可知,,
∴,
∴,
∴;
(3)解:∵正方形边长为4,
由(1)知,
∴,
∵AE为腰,分两种情况:
①当 时,
∵,,点P、E在反比例数图象上,
,
∴,
②当时,点P与点B重合,
∵,点P、E在反比例数图象上,
∴,
∴;
综上所述,满足条件的m的值为2或.
23.(1)解:∵,,
∴,
∵,,
∴.
∵,
∴,
∵点C在y的正半轴上,
∴;
(2)解:如图,连接,
∵,
∴,
∵,,
∴,
∴,
∴,即是斜边的中线,
过点D作轴交直线于点H,
∵轴,,.
∴,, ,
∴,
在和中,
,
∴,
∴,
∴D,G两点速度相同,
当时,如图1,
∵,
∴,
∴,
当时,D点与O点重合,此时,
如图2,当时,
∵,
∴;
故 .
(3)解:如图3,
连接、、,过点F作于点E,过点P作交x轴于点I,
∴为等腰直角三角形,且,
∴点,.
过点F作交于点M,
则四边形为正方形,
由(2)可得,
∴,
∴,
∵四边形为正方形,
∴
当时,,
∴,
解得,
当时,,
∴,
解得.
∴存在t,使的面积等于面积的2倍,或.
24.(1)解:作轴交轴于点,轴交轴于点,轴交轴于,交于,延长交轴于,
轴,
,
,
在和中,
,
,
,
点坐标为,
,
点坐标为,
同理可得,
,
,
,
四边形为矩形,
,
,
点坐标为,
点坐标为,点坐标为;
(2)解:设点的坐标为,
由(1)得,点坐标为,点坐标为,
,
,
解得,
点的坐标为,
作轴交轴于点,轴交轴于点,
点坐标为,点坐标为,点的坐标为,
则,
,
的面积为;
(3)解:要使四边形沿所在直线翻折,当点刚好落在轴上,则轴,画出图如图所示,
与轴的交点为点,与轴的交点为点,
,,
,
在和中,
,
(AAS),
,
设,则,
,
,
解得,
为的长,
,
的长为.
25.(1)解:,,
,;
(2)四边形的面积不发生变化,理由如下:
由题可知,,,
,
,
,
,
,
四边形的面积不发生变化;
(3),△的面积为12,
点到的距离是6,
,
,,
当时,在轴的左侧,
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得;
,,,,
是的中点,
,;
当时,在轴的右侧,
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得(舍);
当点在上时,,解得;
,,,,
是的中点,
,;
综上所述:点坐标为,或,.
26.(1)解:∵
∴点关于轴对称点的坐标为,
∵关于直线对称的点
∴关于轴和直线的二次反射点的坐标
∵
∴点关于轴对称点的坐标为,
∵关于直线对称的点
∴关于轴和直线的二次反射点的坐标
∵
∴点关于轴对称点的坐标为,
∵关于直线对称的点
∴关于轴和直线的二次反射点的坐标
故答案为:、、
(2)∵点的坐标是,
∴点关于轴对称点的坐标为,
∴关于直线对称的点,
∴;
(3)∵点
∴点关于轴和直线的二次反射点分别为,
当与有公共点时,
,
解得
当与有公共点时,
解得
综上:或
27.(1)解:∵点A的坐标为,
∴
在中,,
故答案为:5;
(2)解:∵四边形是菱形,
∴,即.
设直线的解析式,函数图象过点,
则,
解得,
∴直线的解析式为:;
(3)解:由,令,,则,则,
①当时,如图所示,
,,
∴,
∴,
②设M到直线的距离为h,
∴
则,
解得,
当时,如图所示,
,,
,
当时,代入,
解得,
代入,
解得,
综上所述或.
28.(1)
解:点坐标为,,
,
梯形的周长为:,
根据PD将梯形COAB的周长平分,
由,
得.
此时点在上;
(2)
解:作于,于,于,
则.
,
,
,
,
,.
;
(3)
解:点只能在或上,
(ⅰ)当点在上时,设点的坐标为.
由,
得,得,
此时.
由,得.
即在7秒时有点(,);
(ⅱ)当点在上时,设点的坐标为.
由,
得,得,
此时.
即在秒时,有点(,).
故在7秒时有点(,),在秒时有点(,),使将梯形的面积分成的两部分.
29.(1)
解:∵交x轴于A,
∴,解得,
∴,
∵交y轴于B,
∴当x=0时,
∴,
∵M为OB中点,
∴,
设过,,
得到,解得,
∴直线AM的解析式是.
(2)
解:过O作直线,为与AM交点,如图1,
∴ 点P1到直线AB的距离等于点O到直线AB的距离
∴此时,
设直线,
∵,
∴
∴,
∵直线AM的解析式是
∴,解得,
此时
∴,
由是直线AB:向下平移8个单位得到的,
把直线AB:向上平移8个单位得到
交直线AM于,此时,
∴由,得,
∴.
综上所述,点P的坐标为,
(3)
解:①过点B作BHAM,过点A作AH⊥BH于点H,如图2,
如图,则,
设直线BH的表达式为:
∵
∴
∵直线BH经过点
∴
∴直线BH的表达式为,
设直线AH的表达式为,
∵,
∴,得到,
又∵直线AH过点
∴,解得
∴直线AH的表达式为,
由 解得
∴此时点H的坐标为;
②过点A作,作BH⊥AH,垂足为点H,则,如图3,
∵,,
∴此时点H的坐标为,
③过点M作AB的平行线,分别过点A、B向AB的平行线作垂线,垂足分别为H1、H2,如图4,此时,
设直线MH1的表达式为
∵
∴
∵直线MH1经过点
∴
∴直线MH1的表达式为,
设直线AH1的表达式为
∵,
则,,
∵过点
∴
解得
∴直线AH1的表达式为
由 解得
∴,
当时,
∵为矩形,
把点经过向左平移4个单位,向上平移8个单位即可得到点H2
∴点H的坐标为,,,.
