沪教版八年级数学下册试题 第20章 《一次函数》 解答题(含答案)
文档属性
| 名称 | 沪教版八年级数学下册试题 第20章 《一次函数》 解答题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 08:25:17 | ||
图片预览




文档简介
第20章 《一次函数》 解答题
一、解答题
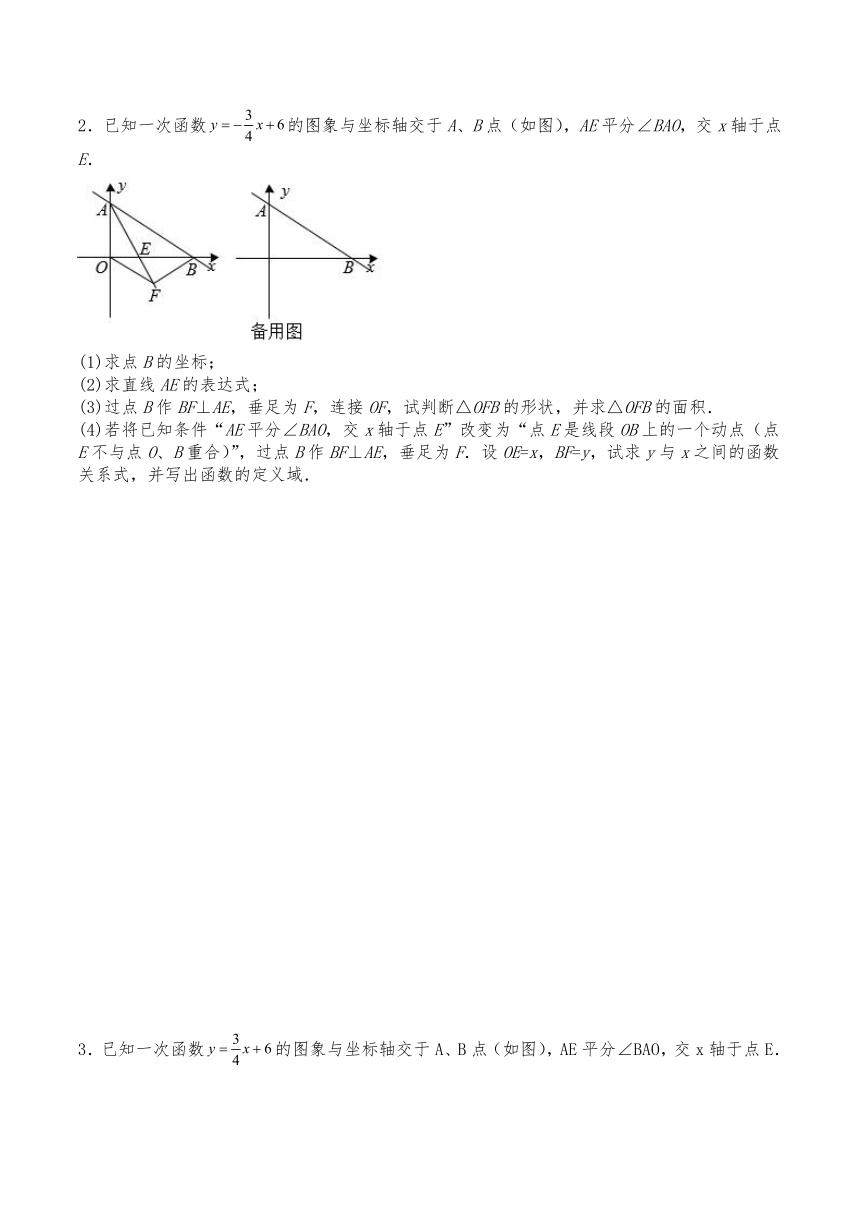
1.已知:如图,在中,,,,AD平分,交BC边于点D.点E是边AB上一动点(与点A、B不重合).过点E作,垂足为点G,与射线AC交于点F.
(1)当点F在边AC上时,
①求证:;
②设,,求y与x之间的函数解析式并写出定义域.
(2)当是等腰三角形时,求BE的长.
2.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
3.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
4.将直角坐标系中一次函数的图像与坐标轴围成的三角形,叫做此一次函数的坐标三角形(也称为直线的坐标三角形).如图,一次函数y=kx-7的图像与x、y轴分别交于点A、B,那么为此一次函数的坐标三角形(也称为直线AB的坐标三角形).
(1)如果点C在x轴上,将沿着直线AB翻折,使点C落在点上,求直线BC的坐标三角形的面积;
(2)如果一次函数y=kx-7的坐标三角形的周长是21,求k值;
(3)在(1)(2)条件下,如果点E的坐标是,直线AB上有一点P,使得周长最小,且点P正好落在某一个反比例函数的图像上,求这个反比例函数的解析式.
5.如图,在中, , ,,点 D 是边 上的动点(点 D 与点 A、B 不重合),过点 D 作 交射线 于点 E,联结 ,点 F是 的中点,联结、、 .
(1)当点 E在边 上(点 E与点C不重合)时,
①设, ,求出y关于x的函数关系式及定义域;
②当平分时,求出的长;
③求证: 是等边三角形.
(2)如果,请直接写出的长
6.如图,直线与轴交于点,与轴交于点,点与点关于轴对称,线与直线、分别交于、.
(1)求直线的函数表达式;
(2)设点是直线上的一动点,过点作轴的平行线,交直线于点,交直线于点,若,则的坐标_______________.
(3)在(2)问条件下,且动点在轴左侧,连接,是轴上的一动点,且,直接写出线段的长.
7.在平面直角坐标系中,给出以下定义:对于x轴上点(其中a为正整数)与坐标平面内一点N,若y轴上存在点T,使得,且,则称点N为a宝点,如示例图,我们可知点为1宝点,理由如下:在x轴上取点,以为斜边作等腰直角三角形,可以算得一个点,它是在y轴上的,因此点为1宝点.
(1)如图①,在点,,,中,2宝点是点___________.(填“A”“B”“C”或“D”)
(2)如图①,点,,若N为4宝点,求点N的坐标.
(3)如图②,若一次函数的图象上存在2宝点,求这个2宝点的坐标.
(4)若一次函数图象上存在无数个3宝点,请直接写出该一次函数的解析式.
8.如图,直线与轴,轴分别交于,两点,直线与轴,轴分别交于,两点,两直线相交于点,已知点的坐标为,点的横坐标为2.
(1)直接写出点、、的坐标;
(2)求出直线的函数表达式;
(3)如图1,求的面积;
(4)如图2,点是线段上任一点,过点作轴的平行线交直线于点,设点的横坐标为,则:
①用表示点、的坐标: , ;
②线段的长度用表示,写出与的函数关系式;
③的面积用表示,写出与的函数关系式.
9.已知:如图,在中,,,,点是边的中点.点是射线上的一动点(点不与点重合),点在的延长线上,且,,垂足为点,交边于点
(1)求证:;
(2)当点在线段上时,设,,求关于的函数解析式,并指出函数的定义域;
(3)当时,直接写出的长
10.【了解概念】对于给定的一次函数(其中k,b为常数,且),则称函数为一次函数(其中k,b为常数,且)的关联函数.
【理解运用】例如:一次函数,它的关联函数为.
(1)点在一次函数的关联函数的图像上,则m的值为______;
(2)已知一次函数.我们可以根据学习函数的经验,对一次函数,它的关联函数为的图像与性质进行探究.下面是小明的探究过程:
①填表,
x … 0 1 2 …
y … 5 3 1 3 5 …
②根据(1)中的结果,请在所给坐标系中画出一次函数的关联函数的图像;
③若,则y的取值范围为______;
【拓展提升】
(3)在平面直角坐标系中,点M、N的坐标分别为、,连接.直接写出线段MN与一次函数的关联函数的图像有1个交点时,b的取值范围为______.
11.(1)问题:如图①,在中,,D为边上一点(不与点B,C重合),将线段绕点A逆时针旋转90°得到,连接,则线段,,之间满足的等量关系式为 ;
(2)探索:如图②,在平面直角坐标系中,的斜边在x轴上,,中,,,将绕点A旋转,使点D落在边上,,试求直线的解析式;
(3)应用:如图③,在平面直角坐标系中,直线交x轴于点B,交y轴于点C,点D在第二象限,,若,,求b的值.
12.如图①,图形l外一点P与图形l上各点连接的所有线段中,若线段最短,则线段的长度称为点P到图形l的距离.例如:图②中,线段的长度是点到线段的距离;线段的长度是点到线段的距离.如图③,在平面直角坐标系中,点A、B、D的坐标分别为,直线与x轴相交于点C.点为x轴上一动点,设点P到线段的距离为d.
(1)① ;
②若,求d的值;
(2)若,求a的值;
(3)若点P在线段上运动,且d为整数,求a的值.
13.设函数(为常数,且),函数和的图象的交点为点.
(1)求证:点在轴的右侧;
(2)已知点在第一象限,函数的值随的增大而增大;
当时,求的取值范围.
若点的坐标是且求证:当时,.
14.如图,在平面直角坐标系中,直线与x轴,y轴分别交于,两点,直线y=-x+1与x轴,y轴分别交于C,D两点,这两条直线相交于点P.
(1)求直线的关系式;
(2)求四边形的面积:
(3)E在直线上,F在直线上,当轴,轴于H,轴于G,
①设E点横坐标为a,当时,四边形的周长L与a之间的关系式为______;
②当时,a=______.
15.如图,在中,,,,将一个角的顶点放在边上移动,使这个角的两边分别与的边、交于点、,且.
(1)如图,当点与点重合时,求的长.
(2)如图,设,,求关于的函数解析式,并写出定义域.
(3)连接,若是直角三角形,直接写出的长.
16.问题发现.
(1)如图,等腰直角置于平面直角坐标系中,点,的坐标分别为,,是上一点,,则点的坐标为______.
(2)问题探究:如图,若点,的坐标分别为,,其余条件与相同,求经过,两点的直线表达式.
(3)问题解决:国庆前夕,某景区为了提高服务质量,想尽可能美化每一个角落,给游客美的享受.如图,是景区东门的广场一角,,两面墙互相垂直,景区管理部门设计将,墙面布置成历史故事宣传墙,边上用建筑隔板搭出段将该角落与广场其他区域隔开,段布置成时事政治宣传墙,剩余部分为广场角出入口,内部空间放置一些绿植和供游人休息的桌椅,考虑到防疫安全,还需在靠近出入口的处建一个体温检测点.已知,,平分,体温检测点在与的交点处.求点分别到,墙面的距离.
17.函数图象是研究函数的重要工具,类比一次函数的学习,对函数的图象与性质进行探究.下表是探究过程中的部分信息:
x … 0 1 2 …
… 4 a 1 4 …
请按要求完成下列各小题:
(1)a的值为______;
(2)在图中画出该函数的图象;
(3)结合函数的图象,解决下列问题:
①下列说法正确的是:______.(填所有正确选项)
A.函数图像关于x轴对称
B.当时,函数有最小值,最小值为
C.当时,y随x的增大而增大
②直接写出不等式的解集为______.
(4)将该函数图像在直线上方的部分保持不变,下方的部分图像沿直线进行翻折,得到新函数图像,若经过点的一次函数图像与新函数图像W只有1个交点时,请直接写出k满足的条件______.
18.在中,,点P为边上的动点,速度为.
(1)如图1,点D为边上一点,,动点P从点D出发,在的边上沿D→B→C的路径匀速运动,当到达点C时停止运动.设的面积为(cm2),的面积为(),点P运动的时间为t(). ,与t之间的函数关系如图2所示,根据题意解答下列问题:
①在图1中, , ;
②在图2中,求和的交点H的坐标;
(2)在(1)的条件下,如图3,若点P,点Q同时从点A出发,在的边上沿A→B→C的路径匀速运动,点Q运动的速度为,当点P到达点C时,点P与点Q同时停止运动.求t为何值时,最大?最大值为多少?
答案
一、解答题
1.(1)①∵,,
∴∠BAC=60°,
∵AD平分,
∴∠FAG=∠EAG,
∵,
∴∠AGF=∠AGE=90°,
又∵AG=AG,
∴ AGF AGE,
∴FG=EG,
∴AD垂直平分FE,
∴DE=DF;
②∵在中,,,,
∴AB=2AC=12,
(a)当点F在线段AC上时,如图,
∵,,
∴AE=12-x,
∵ AGF AGE,
∴AF=AE=12-x,
∴y=6-(12-x)=x-6,
∵0<AF≤6,
∴0<12-x≤6,
∴6≤x<12;
(b)当点F在AC的延长线上时,如图,
∵,,
∴AF=AE=12-x,
∴y=12-x-6=6-x,
∵6<AF,
∴6<12-x,
∴0<x<6;
综上所述:y与x之间的函数解析式为:;
(2)①当是等腰三角形时,∠AFD是顶角,即FA=FD时,如图
∵,
∴AF=FD=6-y,
∵∠FAG=∠EAG=∠BAC=30°,
∴∠FDG=∠FAG=30°,
∵∠C=90°,∠ADC=90°-30°=60°,
∴∠CDF=30°,
∴DF=2CF,
∴6-y=2y,解得:y=2,
∴AF=6-2=4,
∴AE=AF=4,
∴BE=12-4=8;
②当是等腰三角形时,∠FAD是顶角,即FA=DA时,如图,
∵∠ACD=90°,∠CAD=30°,AC=6,
∴AD=2CD=2×(6÷)=4,
∴AE=AF=4,
∴BE=12-4;
③当是等腰三角形时,∠ADF是顶角,即DF=DA时,如图,
∵DC⊥AF,
∴CF=CA=6,
∴AF=12,
∴AE=AF=12,此时,点E与点B重合,舍去,
综上所述:BE=8或12-4.
2.
(1)
解:对于,
当时,;当时,,
,,
在中,根据勾股定理得:,
则,;
(2)
解:过点作,垂足为(如图1所示),
平分,,,
,
在和中,
,
,
,
设,则有,,
在中,,,,
根据勾股定理得:,
解得:,
,
设直线的表达式为,
将,代入得:
,
解得:,
则直线的表达式为;
(3)
解:延长交轴于点(如图2所示),
平分,
,
又,
,
在和中,
,
,
,即为的中点,
又为直角三角形,
,
为等腰三角形,
过点作,垂足为(如图2所示),
,,
,
点的横坐标为,
设,将代入,得:,
,
则;
(4)
解:在中,,,
根据勾股定理得:,
又,(等积法),
,又,
则.
3.解: (1)如图1中,
∵一次函数y=-x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,
,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8-x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b则
,解得,
∴直线AE的解析式为y=-2x+6.
(2)由(1)可知OE=3,AE=,EB=5,
∵S△AEB= EB OA= AE BF,
∴BF=.
(3)如图2中,
在Rt△AOE中,,
∴AE=,
∵S△AEB= EB OA= AE BF,
∴BF=,
∴y=(0<x<8).
4.(1)∵将代入,得:,
∴点B(0,-7),
∴,
又∵点D(0,18),即,
∴,
由翻折的性质可得:,
在Rt△BOC中,由勾股定理可得:,
∴直线BC的坐标三角形的面积;
(2)设,,
∵在Rt△AOB中,由勾股定理可得:,即,
解得:,
∴点A(,0),
∵将点A(,0)代入,得:,
∴,
(3)如图,连接CE交AB于点P,
∵点C与点D关于直线AB对称,
∴,
∴,
∴当点P、C、E在一条直线上时,有最小值,
又∵DE的长度不变,
∴当点P、C、E在一条直线上时,△DPE的周长最小,
设直线CE的解析式,
将点C(-24,0)、E(0,8)代入上式,得:,
解得:,
∴直线CE的解析式,
联立,
解得:,
∴点P(-9,5),
设反比例函数解析式为,
∴,
∴反比例函数解析式为.
5.(1)解:①∵,
∴,
∴,
∵,
∴,
∴,
∵ ,
∴;
②∵平分,,
∴,
在中,,
∴ ,
∴ ,
解得,
∴;
③证明:在和中,,
∵点F是的中点,
∴, ,
∴,
∴,.
∴,
即.
∵,
∴,
∴,
∴是等边三角形.
(2)∵,,,
∴,,
在中,,
当点E在上时,,
当点E在射线上时,如图,
∴,
∴的长是1或2.
6.(1)解:直线与轴交于点,与轴交于点,
∴,,则,,
∵点与点关于轴对称,
∴,
设直线的函数表达式为,
∴,则,
∴直线的函数表达式为.
(2)解:根据题意画图如下所示,
∵点在直线上,点在直线于,
∴设,,则,
∵,即,解方程得,,
∴或.
(3)解:∵点,关于轴对称,
∴,,
∵轴,
∴,
∴在中,,
设交于轴于,则,
∴,,
∵,
∴,
作于,则,
∴,,
如图所示,过点作轴的平行线交轴于,过作的垂线交的延长线于,
∴,
∴,
∴,
∴,
∴,,
设,
∴,且,,
∴,则,
∴,设直线为,
∴,解方程组得,,
∴直线为,
∴,
当在点下方时,设为,
∵,作于,
同理可得:,
同理可得直线为,
令,,
∴,
∴的长为或.
7.(1)解:在x轴上取点,由宝点的定义可知,
点D符合,如图,此时y轴上存在点,符合题意,
故答案为D;
(2)解:如图,连接,将线段绕点T分别逆时针和顺时针旋转,可得点N的坐标,由图可得,点N的坐标为或;
(3)解:设2宝点为点
①当在x轴上方时,过作轴于F,如图所示:
∵是2的宝点,
∴
∴
∵
∴
∴,
设,则
∴
将代入得:
,解得,∴
②当在x轴下方时,过作轴于H,如图所示:
同①可证明,
∴,
设,则
∴,
将代入得:
,解得
∴
综上所述,点的坐标为(2,4)或(0,-2)
(4)解:如图,由题意可得,
①如左图,当点N在第一象限时,设点,则点,
所以符合条件的一次函数解析式为;
②如右图,当点N在第二象限时,设点,则点,
所以符合条件的一次函数解析式为.
8.(1)解:在直线中,
令可得,令可得,令可得,
,,;
(2)解:设直线的解析式为,
∴,解得
直线的解析式为;
(3)解:直线的解析式为,
点,
;
(4)解:①点是线段上任一点,过点作轴的平行线交直线于点,设点的横坐标为,
则:,,
故答案为:,;
②线段的长度,
与的函数关系式为;
③,
与的函数关系式为.
9.(1)证明:∵点是边的中点.
∴,
在和中,
,
∴,
∴,
∴;
(2)连接, ∵,
∴,
∵,,
∴是的垂直平分线,
∴,
∵,,,
∴,
∴,
由勾股定理得,,,
∴,
∵,,
即,
整理得,;
当,重合时,如图,
此时,,
∴,
解得:,,
当,重合时,如图,
此时,,,
同理可得:,,
∴,
∴.
(3)当点E在线段上时,,即,
∴ ,
解得,,即,
当点E在线段的延长线上时,如图2,连接,,
由(1)得,, ,
∴,
即,
解得,, 即
综上所述,当时,或.
10.(1)解∶由题意得的关联函数为,
∵点在一次函数的关联函数的图像上,且,
∴把代入,得, ,
解得,
故答案为∶5;
(2)解:②作图如下,
③∵当时,,当x=0时,
∴时,,
∵当x=0时,当时,,
∴时,,
∴时,;
(3)解:如图,
设直线为,
∵点M、N的坐标分别为、,
∴,
解得,
∴直线为,
令,则,
∴直线为与y轴的交点为,
由题意得,一次函数的关联函数为.
当y轴右侧部分与有交点时,把和代入,得,
当y轴左侧部分与MN有交点时,把和,代入,得,
当,,
∴或者,
∴关联函数与有1个交点时, b的取值范围为∶或者,
故答案为∶ 或者.
11.解:(1)∵,
∴,
即,
∵,,
∴,
∴,
∴;
故答案为:;
(2)连接,如图所示:
∵,
∴,
∴,
∵,,
∴,
∴,,
∵,,
∴,
∴,
∴,
∴,
∴,
∴,
∴,,
设直线的解析式为,把,代入得:
,解得:,
∴直线的解析式为:;
(3)过点O作,交的延长线于点E,连接,
∵,,
∴,
∴,
∴,
把代入得:,即,
把代入得:,即,
∴,
∵,
∴,
即,
∴,
∴,,
∴,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
解得:或(舍去),
∴b的值为5.
12.(1)①设直线的解析式为,
∴,
解得:.
∴直线的解析式为.
令,则,
∴,
∴.
∴.
过点A作于点E,如图,
则.
∴.
∴.
∴.
∴.
故答案为:45;
②若,点P与点E重合,
∴线段的长度为点P到线段的距离d,
∴;
(2)①当点P在点E的左侧时,的长为P到线段的距离d,
∵,,
∴点P与点C重合.
∴①.
②当点P在点E的右侧时,点P到线段的垂线段的长度为P到线段的距离d,
过点A作交x轴于点F,如图,
∵,
∴,.
∴点P与点F重合.
∵,
∴.
∴.
综上,若,a的值为1或3;
(3)①当点P在点E的左侧时,的长为P到线段的距离d,
∵,d为整数,
∴当,即,如图,
∴.
∴.
∴.
∴.
②当点P与点E重合时,,符合题意,
∴.
∴.
③当点P在点E的右侧时,点P到线段的垂线段的长度为P到线段的距离d,
过点P作于点H,如图,
当时,即,
∵,
∴.
∴.
∴.
当时,即,
∵,
∴.
∴,不合题意.
综上,若点P在线段上运动,且d为整数,则a的值为或1或.
13.(1)证明:令,解得,
函数和的图象的交点的横坐标为1,
点在轴的右侧;
(2)解:函数的值随的增大而增大,
由(1)知
点在第一象限,
当时,,
即
,
此时满足
的取值范围是;
证明:点的坐标是,
且
,
当时,
,
,
,
,
,
.
14.(1)解:由已知得:,代入中得:
解得:
∴直线的关系式为
(2)解:如图,过点P作轴,交x轴于点Q,
点P为直线与直线的交点,联立两直线关系式得:
解得:
即
∴梯形的面积
∵三角形为直角三角形
∴三角形的面积
∴四边形面积
(3)解:①由题意可知,四边形为矩形,
∵E在直线上,且设E点横坐标为a
∴
∵F在直线上,当轴,轴于H,轴于G
∴,,
当时,E点位于F点上方
∴,
∴
故答案为:.
②当时,,解得:,不符合题意,舍去
当时,通过画图观察,四边形分为E点在F点上方和F点在E点上方两种情况
当E点在F点上方时
,
此时
若,解得:,符合题意
当F点在E点上方时,
,
此时
若,解得:,符合题意
综上所述:当时,或
故答案为:或.
15.(1),
,
,,
,
,
,
,
,
,
,
,
,,
,
;
(2),,
,
是等边三角形,
,
,
,
,
,
,
,
角的两边分别与的边、交于点、,
过作于,最后只能到点,
此时是,
函数的定义域即的取值范围是:;
(3)如图中,当时,
,,,
,
,
,
,
解得:,
即;
当时,如图2,
,
,
解得:,
即;
综上所述:或.
16.(1)如图,过作于,
∴,
∵是等腰直角三角形,点,的坐标分别为,,
∴,,
∴是等腰直角三角形,
∴,
∵,
∴,
∴,
∴点的坐标为,
故答案为:;
(2)如图,过作于,
∴,
∵点,的坐标分别为,,
∴,,
∴,
∵
∴,
设直线的解析式为,
则,
∴,
∴直线的解析式为,
设,
∴,,
∴,
∵,
∴,
解得或(不合题意舍去),
∴,
设直线的解析式为,
∴,
∴,
∴直线的解析式为;
(3)如图,以点为坐标原点建立平面直角坐标系,
由得直线的解析式为,
过作于,
∵平分,,
∴,
∵,
∴,
∴,
由知,,
∴,
∵,
∴,
∴,
∴,
设直线的解析式为,
则,
∴
∴直线的解析式为,
∴,
解得,,
∴点分别到,墙面的距离分别为,
17.(1)解:把代入得:
,
即,
故答案为:1.
(2)解:该函数的图象,如图所示:
(3)解:①A.函数图像关于y轴对称,故A错误;
B.当时,函数有最小值,最小值为,故B正确;
C.当时,y随x的增大而增大,故C正确;
故答案为:BC;
②根据函数图象可知,当或时,;
故答案为:或;
(4)解:如图所示:
设点,,,,,
设的解析式为,把,代入得:
,
解得:,
的解析式为:,
设的解析式为,把,代入得:
,
解得:,
的解析式为:,
设的解析式为,把,代入得:
,
解得:,
的解析式为:,
根据图像可知,当直线经过和点时,直线与图像W只有一个交点,
把,代入得:,
解得:;
∵,
∴,
根据图像可知,当直线与平行时,直线与图像W只有一个交点,且此时直线绕点继续逆时针旋转,直到与平行之前,直线与图像W只有一个交点,
∴当或时,直线与图像W只有一个交点;
综上分析可知,当或或时直线与图像W只有一个交点.
故答案为:或或.
18.(1)①由图2可知,,,
∴(),
故答案为:5,6;
②如图1,过点A作于T,
∵,,
∴(),
∴(),
∴(),
∴当时,即,
此时点P是的中点,
∴,
∴,
∴点;
(2)①当时,P,Q均在上,
∴当时,最大,
②当时,P在上,Q在上,
∴,
∴当时,最大,
③当时,P,Q均在上,
∴,
∴当时,最大,
∴综上,时,最大值为5.5.
一、解答题
1.已知:如图,在中,,,,AD平分,交BC边于点D.点E是边AB上一动点(与点A、B不重合).过点E作,垂足为点G,与射线AC交于点F.
(1)当点F在边AC上时,
①求证:;
②设,,求y与x之间的函数解析式并写出定义域.
(2)当是等腰三角形时,求BE的长.
2.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
3.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
4.将直角坐标系中一次函数的图像与坐标轴围成的三角形,叫做此一次函数的坐标三角形(也称为直线的坐标三角形).如图,一次函数y=kx-7的图像与x、y轴分别交于点A、B,那么为此一次函数的坐标三角形(也称为直线AB的坐标三角形).
(1)如果点C在x轴上,将沿着直线AB翻折,使点C落在点上,求直线BC的坐标三角形的面积;
(2)如果一次函数y=kx-7的坐标三角形的周长是21,求k值;
(3)在(1)(2)条件下,如果点E的坐标是,直线AB上有一点P,使得周长最小,且点P正好落在某一个反比例函数的图像上,求这个反比例函数的解析式.
5.如图,在中, , ,,点 D 是边 上的动点(点 D 与点 A、B 不重合),过点 D 作 交射线 于点 E,联结 ,点 F是 的中点,联结、、 .
(1)当点 E在边 上(点 E与点C不重合)时,
①设, ,求出y关于x的函数关系式及定义域;
②当平分时,求出的长;
③求证: 是等边三角形.
(2)如果,请直接写出的长
6.如图,直线与轴交于点,与轴交于点,点与点关于轴对称,线与直线、分别交于、.
(1)求直线的函数表达式;
(2)设点是直线上的一动点,过点作轴的平行线,交直线于点,交直线于点,若,则的坐标_______________.
(3)在(2)问条件下,且动点在轴左侧,连接,是轴上的一动点,且,直接写出线段的长.
7.在平面直角坐标系中,给出以下定义:对于x轴上点(其中a为正整数)与坐标平面内一点N,若y轴上存在点T,使得,且,则称点N为a宝点,如示例图,我们可知点为1宝点,理由如下:在x轴上取点,以为斜边作等腰直角三角形,可以算得一个点,它是在y轴上的,因此点为1宝点.
(1)如图①,在点,,,中,2宝点是点___________.(填“A”“B”“C”或“D”)
(2)如图①,点,,若N为4宝点,求点N的坐标.
(3)如图②,若一次函数的图象上存在2宝点,求这个2宝点的坐标.
(4)若一次函数图象上存在无数个3宝点,请直接写出该一次函数的解析式.
8.如图,直线与轴,轴分别交于,两点,直线与轴,轴分别交于,两点,两直线相交于点,已知点的坐标为,点的横坐标为2.
(1)直接写出点、、的坐标;
(2)求出直线的函数表达式;
(3)如图1,求的面积;
(4)如图2,点是线段上任一点,过点作轴的平行线交直线于点,设点的横坐标为,则:
①用表示点、的坐标: , ;
②线段的长度用表示,写出与的函数关系式;
③的面积用表示,写出与的函数关系式.
9.已知:如图,在中,,,,点是边的中点.点是射线上的一动点(点不与点重合),点在的延长线上,且,,垂足为点,交边于点
(1)求证:;
(2)当点在线段上时,设,,求关于的函数解析式,并指出函数的定义域;
(3)当时,直接写出的长
10.【了解概念】对于给定的一次函数(其中k,b为常数,且),则称函数为一次函数(其中k,b为常数,且)的关联函数.
【理解运用】例如:一次函数,它的关联函数为.
(1)点在一次函数的关联函数的图像上,则m的值为______;
(2)已知一次函数.我们可以根据学习函数的经验,对一次函数,它的关联函数为的图像与性质进行探究.下面是小明的探究过程:
①填表,
x … 0 1 2 …
y … 5 3 1 3 5 …
②根据(1)中的结果,请在所给坐标系中画出一次函数的关联函数的图像;
③若,则y的取值范围为______;
【拓展提升】
(3)在平面直角坐标系中,点M、N的坐标分别为、,连接.直接写出线段MN与一次函数的关联函数的图像有1个交点时,b的取值范围为______.
11.(1)问题:如图①,在中,,D为边上一点(不与点B,C重合),将线段绕点A逆时针旋转90°得到,连接,则线段,,之间满足的等量关系式为 ;
(2)探索:如图②,在平面直角坐标系中,的斜边在x轴上,,中,,,将绕点A旋转,使点D落在边上,,试求直线的解析式;
(3)应用:如图③,在平面直角坐标系中,直线交x轴于点B,交y轴于点C,点D在第二象限,,若,,求b的值.
12.如图①,图形l外一点P与图形l上各点连接的所有线段中,若线段最短,则线段的长度称为点P到图形l的距离.例如:图②中,线段的长度是点到线段的距离;线段的长度是点到线段的距离.如图③,在平面直角坐标系中,点A、B、D的坐标分别为,直线与x轴相交于点C.点为x轴上一动点,设点P到线段的距离为d.
(1)① ;
②若,求d的值;
(2)若,求a的值;
(3)若点P在线段上运动,且d为整数,求a的值.
13.设函数(为常数,且),函数和的图象的交点为点.
(1)求证:点在轴的右侧;
(2)已知点在第一象限,函数的值随的增大而增大;
当时,求的取值范围.
若点的坐标是且求证:当时,.
14.如图,在平面直角坐标系中,直线与x轴,y轴分别交于,两点,直线y=-x+1与x轴,y轴分别交于C,D两点,这两条直线相交于点P.
(1)求直线的关系式;
(2)求四边形的面积:
(3)E在直线上,F在直线上,当轴,轴于H,轴于G,
①设E点横坐标为a,当时,四边形的周长L与a之间的关系式为______;
②当时,a=______.
15.如图,在中,,,,将一个角的顶点放在边上移动,使这个角的两边分别与的边、交于点、,且.
(1)如图,当点与点重合时,求的长.
(2)如图,设,,求关于的函数解析式,并写出定义域.
(3)连接,若是直角三角形,直接写出的长.
16.问题发现.
(1)如图,等腰直角置于平面直角坐标系中,点,的坐标分别为,,是上一点,,则点的坐标为______.
(2)问题探究:如图,若点,的坐标分别为,,其余条件与相同,求经过,两点的直线表达式.
(3)问题解决:国庆前夕,某景区为了提高服务质量,想尽可能美化每一个角落,给游客美的享受.如图,是景区东门的广场一角,,两面墙互相垂直,景区管理部门设计将,墙面布置成历史故事宣传墙,边上用建筑隔板搭出段将该角落与广场其他区域隔开,段布置成时事政治宣传墙,剩余部分为广场角出入口,内部空间放置一些绿植和供游人休息的桌椅,考虑到防疫安全,还需在靠近出入口的处建一个体温检测点.已知,,平分,体温检测点在与的交点处.求点分别到,墙面的距离.
17.函数图象是研究函数的重要工具,类比一次函数的学习,对函数的图象与性质进行探究.下表是探究过程中的部分信息:
x … 0 1 2 …
… 4 a 1 4 …
请按要求完成下列各小题:
(1)a的值为______;
(2)在图中画出该函数的图象;
(3)结合函数的图象,解决下列问题:
①下列说法正确的是:______.(填所有正确选项)
A.函数图像关于x轴对称
B.当时,函数有最小值,最小值为
C.当时,y随x的增大而增大
②直接写出不等式的解集为______.
(4)将该函数图像在直线上方的部分保持不变,下方的部分图像沿直线进行翻折,得到新函数图像,若经过点的一次函数图像与新函数图像W只有1个交点时,请直接写出k满足的条件______.
18.在中,,点P为边上的动点,速度为.
(1)如图1,点D为边上一点,,动点P从点D出发,在的边上沿D→B→C的路径匀速运动,当到达点C时停止运动.设的面积为(cm2),的面积为(),点P运动的时间为t(). ,与t之间的函数关系如图2所示,根据题意解答下列问题:
①在图1中, , ;
②在图2中,求和的交点H的坐标;
(2)在(1)的条件下,如图3,若点P,点Q同时从点A出发,在的边上沿A→B→C的路径匀速运动,点Q运动的速度为,当点P到达点C时,点P与点Q同时停止运动.求t为何值时,最大?最大值为多少?
答案
一、解答题
1.(1)①∵,,
∴∠BAC=60°,
∵AD平分,
∴∠FAG=∠EAG,
∵,
∴∠AGF=∠AGE=90°,
又∵AG=AG,
∴ AGF AGE,
∴FG=EG,
∴AD垂直平分FE,
∴DE=DF;
②∵在中,,,,
∴AB=2AC=12,
(a)当点F在线段AC上时,如图,
∵,,
∴AE=12-x,
∵ AGF AGE,
∴AF=AE=12-x,
∴y=6-(12-x)=x-6,
∵0<AF≤6,
∴0<12-x≤6,
∴6≤x<12;
(b)当点F在AC的延长线上时,如图,
∵,,
∴AF=AE=12-x,
∴y=12-x-6=6-x,
∵6<AF,
∴6<12-x,
∴0<x<6;
综上所述:y与x之间的函数解析式为:;
(2)①当是等腰三角形时,∠AFD是顶角,即FA=FD时,如图
∵,
∴AF=FD=6-y,
∵∠FAG=∠EAG=∠BAC=30°,
∴∠FDG=∠FAG=30°,
∵∠C=90°,∠ADC=90°-30°=60°,
∴∠CDF=30°,
∴DF=2CF,
∴6-y=2y,解得:y=2,
∴AF=6-2=4,
∴AE=AF=4,
∴BE=12-4=8;
②当是等腰三角形时,∠FAD是顶角,即FA=DA时,如图,
∵∠ACD=90°,∠CAD=30°,AC=6,
∴AD=2CD=2×(6÷)=4,
∴AE=AF=4,
∴BE=12-4;
③当是等腰三角形时,∠ADF是顶角,即DF=DA时,如图,
∵DC⊥AF,
∴CF=CA=6,
∴AF=12,
∴AE=AF=12,此时,点E与点B重合,舍去,
综上所述:BE=8或12-4.
2.
(1)
解:对于,
当时,;当时,,
,,
在中,根据勾股定理得:,
则,;
(2)
解:过点作,垂足为(如图1所示),
平分,,,
,
在和中,
,
,
,
设,则有,,
在中,,,,
根据勾股定理得:,
解得:,
,
设直线的表达式为,
将,代入得:
,
解得:,
则直线的表达式为;
(3)
解:延长交轴于点(如图2所示),
平分,
,
又,
,
在和中,
,
,
,即为的中点,
又为直角三角形,
,
为等腰三角形,
过点作,垂足为(如图2所示),
,,
,
点的横坐标为,
设,将代入,得:,
,
则;
(4)
解:在中,,,
根据勾股定理得:,
又,(等积法),
,又,
则.
3.解: (1)如图1中,
∵一次函数y=-x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,
,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8-x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b则
,解得,
∴直线AE的解析式为y=-2x+6.
(2)由(1)可知OE=3,AE=,EB=5,
∵S△AEB= EB OA= AE BF,
∴BF=.
(3)如图2中,
在Rt△AOE中,,
∴AE=,
∵S△AEB= EB OA= AE BF,
∴BF=,
∴y=(0<x<8).
4.(1)∵将代入,得:,
∴点B(0,-7),
∴,
又∵点D(0,18),即,
∴,
由翻折的性质可得:,
在Rt△BOC中,由勾股定理可得:,
∴直线BC的坐标三角形的面积;
(2)设,,
∵在Rt△AOB中,由勾股定理可得:,即,
解得:,
∴点A(,0),
∵将点A(,0)代入,得:,
∴,
(3)如图,连接CE交AB于点P,
∵点C与点D关于直线AB对称,
∴,
∴,
∴当点P、C、E在一条直线上时,有最小值,
又∵DE的长度不变,
∴当点P、C、E在一条直线上时,△DPE的周长最小,
设直线CE的解析式,
将点C(-24,0)、E(0,8)代入上式,得:,
解得:,
∴直线CE的解析式,
联立,
解得:,
∴点P(-9,5),
设反比例函数解析式为,
∴,
∴反比例函数解析式为.
5.(1)解:①∵,
∴,
∴,
∵,
∴,
∴,
∵ ,
∴;
②∵平分,,
∴,
在中,,
∴ ,
∴ ,
解得,
∴;
③证明:在和中,,
∵点F是的中点,
∴, ,
∴,
∴,.
∴,
即.
∵,
∴,
∴,
∴是等边三角形.
(2)∵,,,
∴,,
在中,,
当点E在上时,,
当点E在射线上时,如图,
∴,
∴的长是1或2.
6.(1)解:直线与轴交于点,与轴交于点,
∴,,则,,
∵点与点关于轴对称,
∴,
设直线的函数表达式为,
∴,则,
∴直线的函数表达式为.
(2)解:根据题意画图如下所示,
∵点在直线上,点在直线于,
∴设,,则,
∵,即,解方程得,,
∴或.
(3)解:∵点,关于轴对称,
∴,,
∵轴,
∴,
∴在中,,
设交于轴于,则,
∴,,
∵,
∴,
作于,则,
∴,,
如图所示,过点作轴的平行线交轴于,过作的垂线交的延长线于,
∴,
∴,
∴,
∴,
∴,,
设,
∴,且,,
∴,则,
∴,设直线为,
∴,解方程组得,,
∴直线为,
∴,
当在点下方时,设为,
∵,作于,
同理可得:,
同理可得直线为,
令,,
∴,
∴的长为或.
7.(1)解:在x轴上取点,由宝点的定义可知,
点D符合,如图,此时y轴上存在点,符合题意,
故答案为D;
(2)解:如图,连接,将线段绕点T分别逆时针和顺时针旋转,可得点N的坐标,由图可得,点N的坐标为或;
(3)解:设2宝点为点
①当在x轴上方时,过作轴于F,如图所示:
∵是2的宝点,
∴
∴
∵
∴
∴,
设,则
∴
将代入得:
,解得,∴
②当在x轴下方时,过作轴于H,如图所示:
同①可证明,
∴,
设,则
∴,
将代入得:
,解得
∴
综上所述,点的坐标为(2,4)或(0,-2)
(4)解:如图,由题意可得,
①如左图,当点N在第一象限时,设点,则点,
所以符合条件的一次函数解析式为;
②如右图,当点N在第二象限时,设点,则点,
所以符合条件的一次函数解析式为.
8.(1)解:在直线中,
令可得,令可得,令可得,
,,;
(2)解:设直线的解析式为,
∴,解得
直线的解析式为;
(3)解:直线的解析式为,
点,
;
(4)解:①点是线段上任一点,过点作轴的平行线交直线于点,设点的横坐标为,
则:,,
故答案为:,;
②线段的长度,
与的函数关系式为;
③,
与的函数关系式为.
9.(1)证明:∵点是边的中点.
∴,
在和中,
,
∴,
∴,
∴;
(2)连接, ∵,
∴,
∵,,
∴是的垂直平分线,
∴,
∵,,,
∴,
∴,
由勾股定理得,,,
∴,
∵,,
即,
整理得,;
当,重合时,如图,
此时,,
∴,
解得:,,
当,重合时,如图,
此时,,,
同理可得:,,
∴,
∴.
(3)当点E在线段上时,,即,
∴ ,
解得,,即,
当点E在线段的延长线上时,如图2,连接,,
由(1)得,, ,
∴,
即,
解得,, 即
综上所述,当时,或.
10.(1)解∶由题意得的关联函数为,
∵点在一次函数的关联函数的图像上,且,
∴把代入,得, ,
解得,
故答案为∶5;
(2)解:②作图如下,
③∵当时,,当x=0时,
∴时,,
∵当x=0时,当时,,
∴时,,
∴时,;
(3)解:如图,
设直线为,
∵点M、N的坐标分别为、,
∴,
解得,
∴直线为,
令,则,
∴直线为与y轴的交点为,
由题意得,一次函数的关联函数为.
当y轴右侧部分与有交点时,把和代入,得,
当y轴左侧部分与MN有交点时,把和,代入,得,
当,,
∴或者,
∴关联函数与有1个交点时, b的取值范围为∶或者,
故答案为∶ 或者.
11.解:(1)∵,
∴,
即,
∵,,
∴,
∴,
∴;
故答案为:;
(2)连接,如图所示:
∵,
∴,
∴,
∵,,
∴,
∴,,
∵,,
∴,
∴,
∴,
∴,
∴,
∴,
∴,,
设直线的解析式为,把,代入得:
,解得:,
∴直线的解析式为:;
(3)过点O作,交的延长线于点E,连接,
∵,,
∴,
∴,
∴,
把代入得:,即,
把代入得:,即,
∴,
∵,
∴,
即,
∴,
∴,,
∴,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
解得:或(舍去),
∴b的值为5.
12.(1)①设直线的解析式为,
∴,
解得:.
∴直线的解析式为.
令,则,
∴,
∴.
∴.
过点A作于点E,如图,
则.
∴.
∴.
∴.
∴.
故答案为:45;
②若,点P与点E重合,
∴线段的长度为点P到线段的距离d,
∴;
(2)①当点P在点E的左侧时,的长为P到线段的距离d,
∵,,
∴点P与点C重合.
∴①.
②当点P在点E的右侧时,点P到线段的垂线段的长度为P到线段的距离d,
过点A作交x轴于点F,如图,
∵,
∴,.
∴点P与点F重合.
∵,
∴.
∴.
综上,若,a的值为1或3;
(3)①当点P在点E的左侧时,的长为P到线段的距离d,
∵,d为整数,
∴当,即,如图,
∴.
∴.
∴.
∴.
②当点P与点E重合时,,符合题意,
∴.
∴.
③当点P在点E的右侧时,点P到线段的垂线段的长度为P到线段的距离d,
过点P作于点H,如图,
当时,即,
∵,
∴.
∴.
∴.
当时,即,
∵,
∴.
∴,不合题意.
综上,若点P在线段上运动,且d为整数,则a的值为或1或.
13.(1)证明:令,解得,
函数和的图象的交点的横坐标为1,
点在轴的右侧;
(2)解:函数的值随的增大而增大,
由(1)知
点在第一象限,
当时,,
即
,
此时满足
的取值范围是;
证明:点的坐标是,
且
,
当时,
,
,
,
,
,
.
14.(1)解:由已知得:,代入中得:
解得:
∴直线的关系式为
(2)解:如图,过点P作轴,交x轴于点Q,
点P为直线与直线的交点,联立两直线关系式得:
解得:
即
∴梯形的面积
∵三角形为直角三角形
∴三角形的面积
∴四边形面积
(3)解:①由题意可知,四边形为矩形,
∵E在直线上,且设E点横坐标为a
∴
∵F在直线上,当轴,轴于H,轴于G
∴,,
当时,E点位于F点上方
∴,
∴
故答案为:.
②当时,,解得:,不符合题意,舍去
当时,通过画图观察,四边形分为E点在F点上方和F点在E点上方两种情况
当E点在F点上方时
,
此时
若,解得:,符合题意
当F点在E点上方时,
,
此时
若,解得:,符合题意
综上所述:当时,或
故答案为:或.
15.(1),
,
,,
,
,
,
,
,
,
,
,
,,
,
;
(2),,
,
是等边三角形,
,
,
,
,
,
,
,
角的两边分别与的边、交于点、,
过作于,最后只能到点,
此时是,
函数的定义域即的取值范围是:;
(3)如图中,当时,
,,,
,
,
,
,
解得:,
即;
当时,如图2,
,
,
解得:,
即;
综上所述:或.
16.(1)如图,过作于,
∴,
∵是等腰直角三角形,点,的坐标分别为,,
∴,,
∴是等腰直角三角形,
∴,
∵,
∴,
∴,
∴点的坐标为,
故答案为:;
(2)如图,过作于,
∴,
∵点,的坐标分别为,,
∴,,
∴,
∵
∴,
设直线的解析式为,
则,
∴,
∴直线的解析式为,
设,
∴,,
∴,
∵,
∴,
解得或(不合题意舍去),
∴,
设直线的解析式为,
∴,
∴,
∴直线的解析式为;
(3)如图,以点为坐标原点建立平面直角坐标系,
由得直线的解析式为,
过作于,
∵平分,,
∴,
∵,
∴,
∴,
由知,,
∴,
∵,
∴,
∴,
∴,
设直线的解析式为,
则,
∴
∴直线的解析式为,
∴,
解得,,
∴点分别到,墙面的距离分别为,
17.(1)解:把代入得:
,
即,
故答案为:1.
(2)解:该函数的图象,如图所示:
(3)解:①A.函数图像关于y轴对称,故A错误;
B.当时,函数有最小值,最小值为,故B正确;
C.当时,y随x的增大而增大,故C正确;
故答案为:BC;
②根据函数图象可知,当或时,;
故答案为:或;
(4)解:如图所示:
设点,,,,,
设的解析式为,把,代入得:
,
解得:,
的解析式为:,
设的解析式为,把,代入得:
,
解得:,
的解析式为:,
设的解析式为,把,代入得:
,
解得:,
的解析式为:,
根据图像可知,当直线经过和点时,直线与图像W只有一个交点,
把,代入得:,
解得:;
∵,
∴,
根据图像可知,当直线与平行时,直线与图像W只有一个交点,且此时直线绕点继续逆时针旋转,直到与平行之前,直线与图像W只有一个交点,
∴当或时,直线与图像W只有一个交点;
综上分析可知,当或或时直线与图像W只有一个交点.
故答案为:或或.
18.(1)①由图2可知,,,
∴(),
故答案为:5,6;
②如图1,过点A作于T,
∵,,
∴(),
∴(),
∴(),
∴当时,即,
此时点P是的中点,
∴,
∴,
∴点;
(2)①当时,P,Q均在上,
∴当时,最大,
②当时,P在上,Q在上,
∴,
∴当时,最大,
③当时,P,Q均在上,
∴,
∴当时,最大,
∴综上,时,最大值为5.5.
