人教版六年级下册立体图形的表面积和体积 课件(共19张PPT)
文档属性
| 名称 | 人教版六年级下册立体图形的表面积和体积 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 657.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 11:35:25 | ||
图片预览


文档简介
(共19张PPT)
立体图形的表面积和体积
总复习
学习目标:
1、掌握长方体、正方体、圆柱体表面积公式
2、掌握长方体正方体圆柱体圆锥体体积公式
3、熟练运用公式解决立体图形问题
整理反思
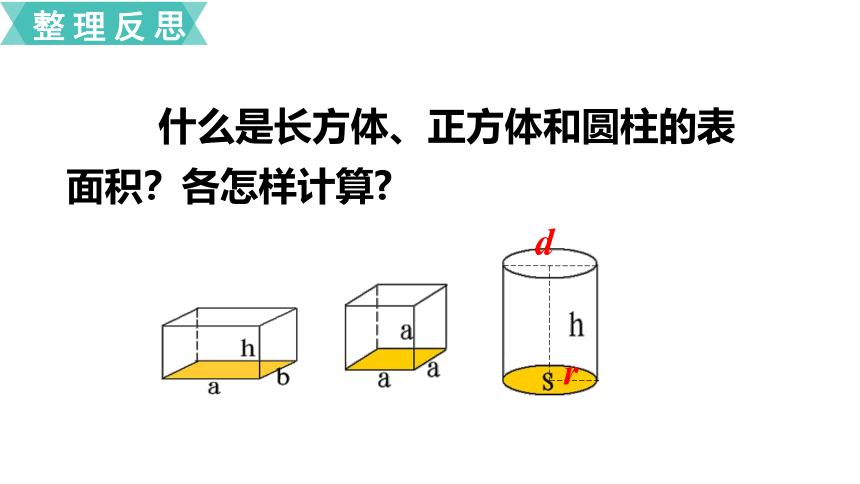
什么是长方体、正方体和圆柱的表面积?各怎样计算
d
r
整理反思
上
下
前
后
左
右
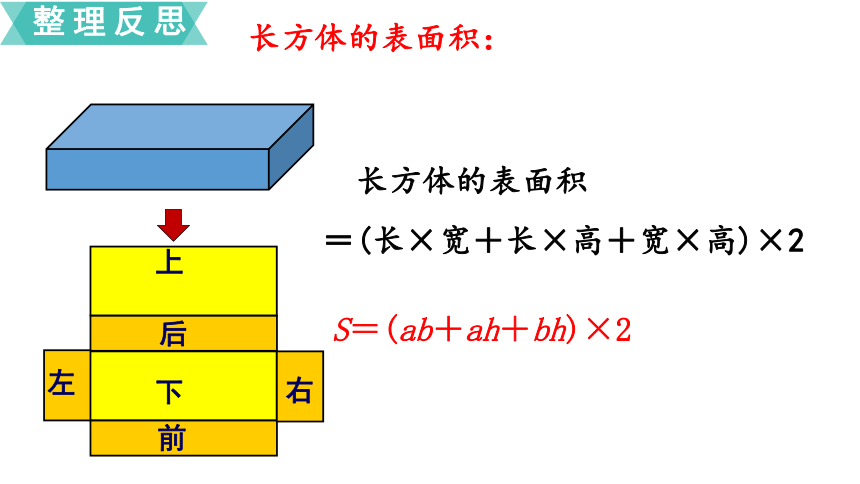
长方体的表面积:
长方体的表面积
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
整理反思
上
下
前
后
左
右
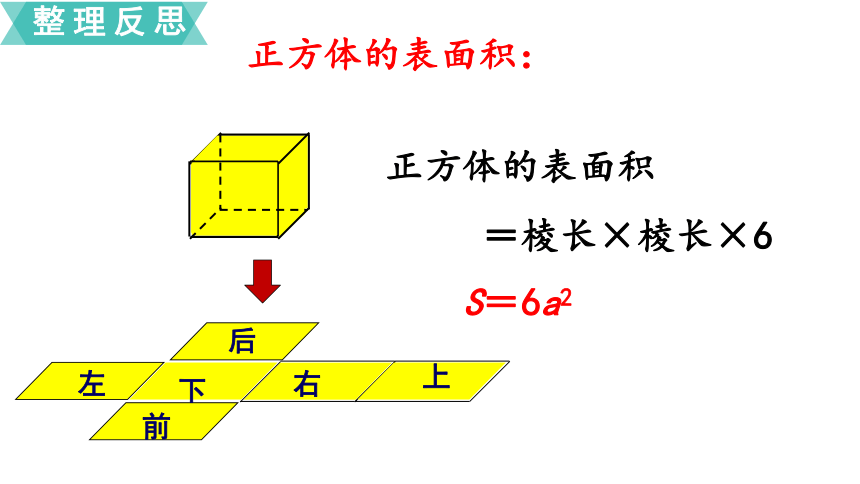
正方体的表面积:
正方体的表面积
=棱长×棱长×6
S=6a2
整理反思
底面
底面
侧面
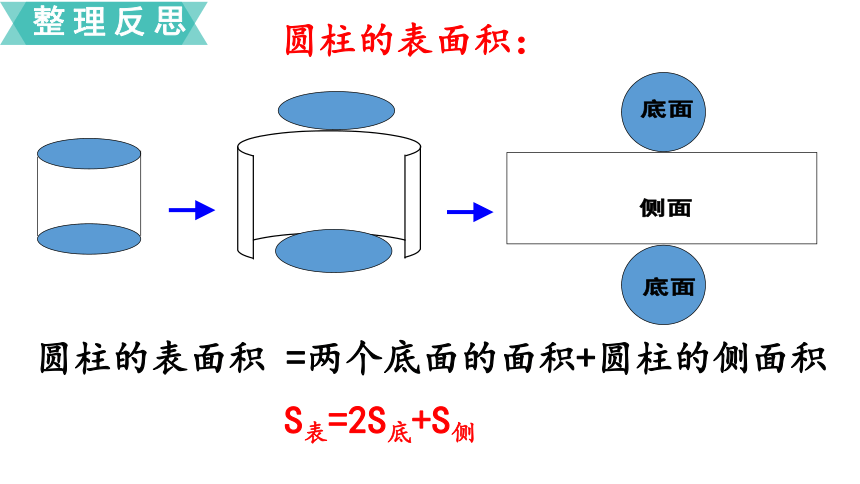
S表=2S底+S侧
圆柱的表面积:
圆柱的表面积 =两个底面的面积+圆柱的侧面积
整理反思
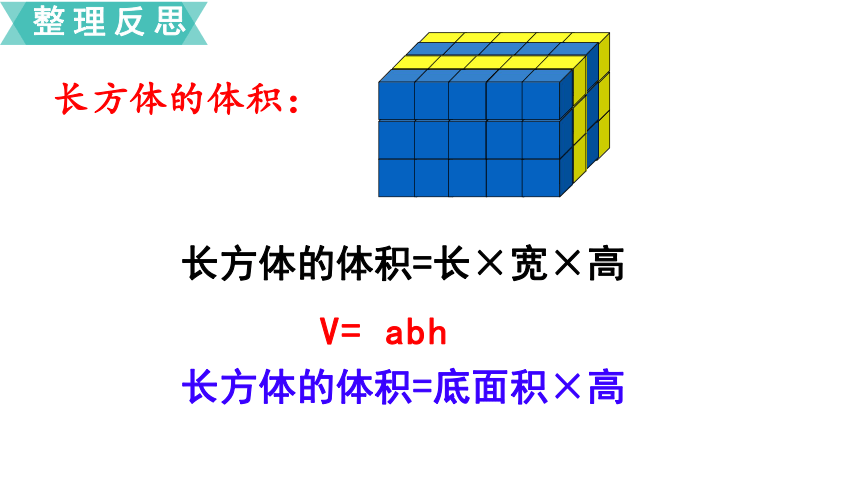
长方体的体积=长×宽×高
V= abh
长方体的体积=底面积×高
长方体的体积:
整理反思
正方体的体积=棱长×棱长×棱长
V=a3
正方体的体积=底面积×高
正方体的体积:
整理反思
圆柱的体积= 底面积 × 高
V =
Sh
圆柱的体积:
V= sh
整理反思
1
3
圆柱的体积= ×底面积 × 高
1
3
圆锥的体积:
整理反思
回忆各立体图形体积公式的推导过程,想一想它们之间的联系,完成下面的填空,与同学交流。
练习实践
表面积:
42 x 6 = 96 (平方厘米)
体 积:
43 = 64 (立方厘米)
1.
练习实践
表面积:
(5x3+4x3+5x4)x2
= (15+12 +20) x 2
= 47 x 2
= 94 (平方厘米)
体积:
5x4x3=60(立方厘米)
2.
练习实践
表面积:
3.14 x 10 x 5=157 (平方厘米)
3.14 x (10÷2) x 2 =157 (平方厘米)
157 + 157 = 314 (平方厘米)
体积:
3.14 x (10÷2)2 x 5= 392.5 (立方厘米)
3.
练习实践
4.
练习实践
侧 面 积 3.14 x 4 x 2 x 12 = 301.44 (平方分米)
两个底面积 3.14 x 42 x 2 = 100.48 (平方分米)
表 面 积 301.44 + 100.48 = 401.92 (平方分米)
答:制作这个油桶至少需要401.92 平方分米铁皮。
5.
练习实践
侧面积 3.14 x 40 x 50 = 6280 (平方厘米)
底面积 3.14 x (40÷2)2 = 1256 (平方厘米)
表面积 6280 + 1256 = 7536 (平方厘米)
答:制作这个水桶至少需要7536平方厘米铁皮。
6.
练习实践
课堂小结
同学们:
通过这节课的学习,你有什么收获?
立体图形的表面积和体积
总复习
学习目标:
1、掌握长方体、正方体、圆柱体表面积公式
2、掌握长方体正方体圆柱体圆锥体体积公式
3、熟练运用公式解决立体图形问题
整理反思
什么是长方体、正方体和圆柱的表面积?各怎样计算
d
r
整理反思
上
下
前
后
左
右
长方体的表面积:
长方体的表面积
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
整理反思
上
下
前
后
左
右
正方体的表面积:
正方体的表面积
=棱长×棱长×6
S=6a2
整理反思
底面
底面
侧面
S表=2S底+S侧
圆柱的表面积:
圆柱的表面积 =两个底面的面积+圆柱的侧面积
整理反思
长方体的体积=长×宽×高
V= abh
长方体的体积=底面积×高
长方体的体积:
整理反思
正方体的体积=棱长×棱长×棱长
V=a3
正方体的体积=底面积×高
正方体的体积:
整理反思
圆柱的体积= 底面积 × 高
V =
Sh
圆柱的体积:
V= sh
整理反思
1
3
圆柱的体积= ×底面积 × 高
1
3
圆锥的体积:
整理反思
回忆各立体图形体积公式的推导过程,想一想它们之间的联系,完成下面的填空,与同学交流。
练习实践
表面积:
42 x 6 = 96 (平方厘米)
体 积:
43 = 64 (立方厘米)
1.
练习实践
表面积:
(5x3+4x3+5x4)x2
= (15+12 +20) x 2
= 47 x 2
= 94 (平方厘米)
体积:
5x4x3=60(立方厘米)
2.
练习实践
表面积:
3.14 x 10 x 5=157 (平方厘米)
3.14 x (10÷2) x 2 =157 (平方厘米)
157 + 157 = 314 (平方厘米)
体积:
3.14 x (10÷2)2 x 5= 392.5 (立方厘米)
3.
练习实践
4.
练习实践
侧 面 积 3.14 x 4 x 2 x 12 = 301.44 (平方分米)
两个底面积 3.14 x 42 x 2 = 100.48 (平方分米)
表 面 积 301.44 + 100.48 = 401.92 (平方分米)
答:制作这个油桶至少需要401.92 平方分米铁皮。
5.
练习实践
侧面积 3.14 x 40 x 50 = 6280 (平方厘米)
底面积 3.14 x (40÷2)2 = 1256 (平方厘米)
表面积 6280 + 1256 = 7536 (平方厘米)
答:制作这个水桶至少需要7536平方厘米铁皮。
6.
练习实践
课堂小结
同学们:
通过这节课的学习,你有什么收获?
同课章节目录
