江苏省常州市新北区实验学校苏科版七年级数学上册《2-6 有理数的乘法》课件
文档属性
| 名称 | 江苏省常州市新北区实验学校苏科版七年级数学上册《2-6 有理数的乘法》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 598.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-23 09:11:58 | ||
图片预览










文档简介
课件35张PPT。2.6 有理数的乘法
学习了负数以后,如何进行下列有理数乘法的运算呢?计算:
5 × 3 ×
0 ×= 0= 15(1):(2):一只蜗牛沿直线l爬行, 它现在的位置恰在l上的点O 活动1l 我们把向右记为正,向左记为负;
几分钟后记为正,几分钟前记为负。按照此
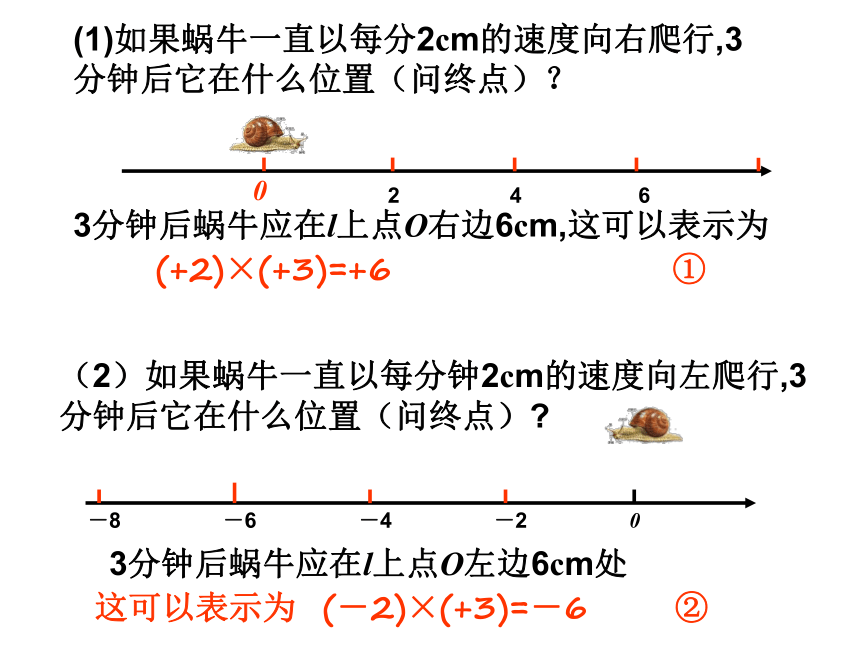
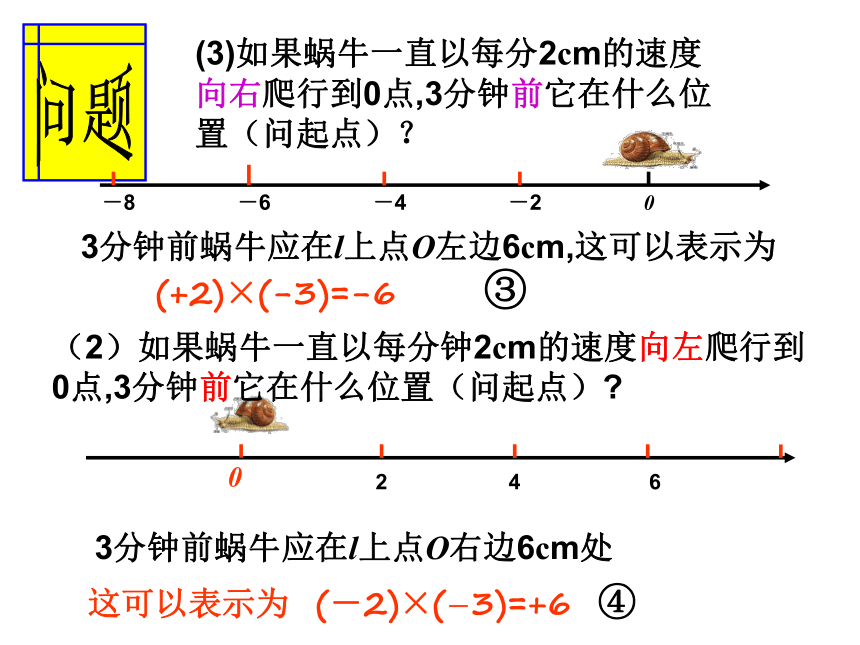
规定,你能用算式表示下列4个问题吗?(1)如果蜗牛一直以每分2cm的速度向右爬行,3分钟后它在什么位置(问终点)?3分钟后蜗牛应在l上点O右边6cm,这可以表示为 3分钟后蜗牛应在l上点O左边6cm处 (2)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置(问终点)? (+2)×(+3)=+6 ① 这可以表示为 (-2)×(+3)=-6 ② (3)如果蜗牛一直以每分2cm的速度向右爬行到0点,3分钟前它在什么位置(问起点)?3分钟前蜗牛应在l上点O左边6cm,这可以表示为 3分钟前蜗牛应在l上点O右边6cm处 (2)如果蜗牛一直以每分钟2cm的速度向左爬行到0点,3分钟前它在什么位置(问起点)? (+2)×(-3)=-6 ③ 这可以表示为 (-2)×(-3)=+6 ④ (+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
仿照上例的情景,探求新知(+4)×(+5) (-5)×(-3)
(-1)×(+6) (+8)×(-2)=+20=+15=-6=-16然后尝试计算下列各题两个有理数相乘的积有哪几种情况?
怎样确定两个有理数的积?议一议?正数×正数=_______正数×负数=_______负数×正数=_______负数×负数=_______正数负数负数正数同号得正,
异号得负。绝对值相乘 0×5=___ , (-5)×0=____
0×(+6)=___
(+6) × 0=____任何数同0相乘,结果有什么特点?想一想?有理数乘法法则(1)两数相乘,同号得正,
异号得负,(2)任何数同0相乘,都得0。并把绝对值相乘。
例 题 解 析例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)解:(1) (?4)×5 (2) (?4)×(?7)
=?(4×5) =+(4×7)
=?20 ; =35;=1 ;=1 ;求解第一步是 ;确定积的符号 第二步
是 ;绝对值相乘例2 计算:
(1) (?4)×5×(?0.25); (2)
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25) =+(20×0.25)=5.=(?20)×(?0.25) 三个有理数相乘,先把前两个相乘, 再把 所得结果与另一数相乘。三个有理数相乘,你会计算吗? 几个有理数相乘,因数都不为 0 时,
积的符号怎样确定? 有一因数为 0 时,积是多少?乘积 的符号 的确定 几个有理数相乘,因数都不为 0 时,
积的符号由 确定:负因数的个数奇数个为负,偶数个为正。 有一因数为 0 时,积是0 。 不计算,只确定积的符号
(1)(-3)× 8 × 2.5
(2)(-3)×(-8)× 2.5看谁说得快用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.<<>>=看谁算得准(1)(﹣5)×8×(﹣7)×(﹣0.25)
(2)(﹣ )× × ×(﹣ )
(3)(﹣1)×(﹣ ) × × ×( ﹣ )
(﹣6) ×0×(﹣1):
本节课我们学习了哪些知识?课时小结2.乘积 的符号 的确定 几个有理数相乘,因数都不为 0 时,
积的符号由 确定:负因数的个数奇数个为负,偶数个为正。 有一因数为 0 时,积是0 。谢谢指导!
课后的整理和消化,是你走向成功的必经之路!
你,做到了吗??
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?解:(-5) ×60=-300
答:销售额减少300元 如果某天空气的温度是:高度每增加1千米, 温度下降5℃,当地面温度是15℃时,求4千米山顶的温度?
用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3km后,气温有什么变化?解:(-6)×3=-18 答:气温下降18°c应用生活数学游戏:1、在整数-5、-3、-1、2、4、6中任取两个数相乘,所得积的最大值与最小值分别是多少?15 1、若|a |=3, |b |=5,则a×b= 。
-15或15 若a,b都是整数,且a×b=2,则a+b的值是 . 已知 a,b 互为相反数, c,d 互为倒数, m 的绝对值为2,求 (a+b)-cd+m的值。
三思而行(1) 若 ab>0,则必有 ( )A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0(2)若ab=0,则一定有( ) a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0DB(3)一个有理数和它的相反数之积( )A. 必为正数 B. 必为负数
C. 一定不大于零 D. 一定等于1(4)若ab=|ab|,则必有( ) a与b同号 B. a与b异号
C. a与b中至少有一个等于0 D. 以上都不对CD三思而行1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?? 小结 ? 思考 ? 同学们,再 见!
学习了负数以后,如何进行下列有理数乘法的运算呢?计算:
5 × 3 ×
0 ×= 0= 15(1):(2):一只蜗牛沿直线l爬行, 它现在的位置恰在l上的点O 活动1l 我们把向右记为正,向左记为负;
几分钟后记为正,几分钟前记为负。按照此
规定,你能用算式表示下列4个问题吗?(1)如果蜗牛一直以每分2cm的速度向右爬行,3分钟后它在什么位置(问终点)?3分钟后蜗牛应在l上点O右边6cm,这可以表示为 3分钟后蜗牛应在l上点O左边6cm处 (2)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置(问终点)? (+2)×(+3)=+6 ① 这可以表示为 (-2)×(+3)=-6 ② (3)如果蜗牛一直以每分2cm的速度向右爬行到0点,3分钟前它在什么位置(问起点)?3分钟前蜗牛应在l上点O左边6cm,这可以表示为 3分钟前蜗牛应在l上点O右边6cm处 (2)如果蜗牛一直以每分钟2cm的速度向左爬行到0点,3分钟前它在什么位置(问起点)? (+2)×(-3)=-6 ③ 这可以表示为 (-2)×(-3)=+6 ④ (+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
仿照上例的情景,探求新知(+4)×(+5) (-5)×(-3)
(-1)×(+6) (+8)×(-2)=+20=+15=-6=-16然后尝试计算下列各题两个有理数相乘的积有哪几种情况?
怎样确定两个有理数的积?议一议?正数×正数=_______正数×负数=_______负数×正数=_______负数×负数=_______正数负数负数正数同号得正,
异号得负。绝对值相乘 0×5=___ , (-5)×0=____
0×(+6)=___
(+6) × 0=____任何数同0相乘,结果有什么特点?想一想?有理数乘法法则(1)两数相乘,同号得正,
异号得负,(2)任何数同0相乘,都得0。并把绝对值相乘。
例 题 解 析例1 计算:
(1) (?4)×5 ; (2) (?4)×(?7) ;
(3) (4)解:(1) (?4)×5 (2) (?4)×(?7)
=?(4×5) =+(4×7)
=?20 ; =35;=1 ;=1 ;求解第一步是 ;确定积的符号 第二步
是 ;绝对值相乘例2 计算:
(1) (?4)×5×(?0.25); (2)
解:(1) (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25) =+(20×0.25)=5.=(?20)×(?0.25) 三个有理数相乘,先把前两个相乘, 再把 所得结果与另一数相乘。三个有理数相乘,你会计算吗? 几个有理数相乘,因数都不为 0 时,
积的符号怎样确定? 有一因数为 0 时,积是多少?乘积 的符号 的确定 几个有理数相乘,因数都不为 0 时,
积的符号由 确定:负因数的个数奇数个为负,偶数个为正。 有一因数为 0 时,积是0 。 不计算,只确定积的符号
(1)(-3)× 8 × 2.5
(2)(-3)×(-8)× 2.5看谁说得快用“>” “<”或“=”号填空:
1﹑如果 a<0, b>0, 那么ab( )0;
2﹑如果 a>0, b<0, 那么ab( )0;
3﹑如果 a<0, b<0, 那么ab( )0;
4﹑如果 a>0, b>0, 那么ab( )0;
5﹑如果 a = 0, b≠0, 那么ab( )0.<<>>=看谁算得准(1)(﹣5)×8×(﹣7)×(﹣0.25)
(2)(﹣ )× × ×(﹣ )
(3)(﹣1)×(﹣ ) × × ×( ﹣ )
(﹣6) ×0×(﹣1):
本节课我们学习了哪些知识?课时小结2.乘积 的符号 的确定 几个有理数相乘,因数都不为 0 时,
积的符号由 确定:负因数的个数奇数个为负,偶数个为正。 有一因数为 0 时,积是0 。谢谢指导!
课后的整理和消化,是你走向成功的必经之路!
你,做到了吗??
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?解:(-5) ×60=-300
答:销售额减少300元 如果某天空气的温度是:高度每增加1千米, 温度下降5℃,当地面温度是15℃时,求4千米山顶的温度?
用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3km后,气温有什么变化?解:(-6)×3=-18 答:气温下降18°c应用生活数学游戏:1、在整数-5、-3、-1、2、4、6中任取两个数相乘,所得积的最大值与最小值分别是多少?15 1、若|a |=3, |b |=5,则a×b= 。
-15或15 若a,b都是整数,且a×b=2,则a+b的值是 . 已知 a,b 互为相反数, c,d 互为倒数, m 的绝对值为2,求 (a+b)-cd+m的值。
三思而行(1) 若 ab>0,则必有 ( )A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0(2)若ab=0,则一定有( ) a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0DB(3)一个有理数和它的相反数之积( )A. 必为正数 B. 必为负数
C. 一定不大于零 D. 一定等于1(4)若ab=|ab|,则必有( ) a与b同号 B. a与b异号
C. a与b中至少有一个等于0 D. 以上都不对CD三思而行1、本节课你最大的收获是什么?
2、有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
3、小学所学的乘法的有关运算律及相关技巧能否用到有理数的乘法中来?? 小结 ? 思考 ? 同学们,再 见!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
