第八章 二元一次方程组单元同步检测试题(含答案)
文档属性
| 名称 | 第八章 二元一次方程组单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 251.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 12:14:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章《二元一次方程组》单元检测题
一、选择题(每题3分,共30分)
1.下面各组数值中,二元一次方程2x+y=10的解是( )
A. B. C. D.
2.解方程组 的最好解法是( )
A.由①得y=3x﹣2,再代入② B.由②得3x=11﹣2y,再代入①
C.由①×2+②消去y D.由②﹣①,消去x
3.已知 是方程 的一组解,那么m的值是( )
4.二元一次方程3x+y=8的正整数解有( )
A.2个 B.3个 C.4个 D.5个
5.若二元一次方程3x﹣y=7,3x+5y=1,y=kx﹣9有公共解,则k的取值为( )
A.5 B.﹣3 C.﹣4 D.4
6.若关于x,y的方程组的解互为相反数,则m的值等于( )
A.1 B.0 C.﹣1 D.2
7.若和是方程的两组解,则m,n的值分别为( )
A., B.2,4 C.4,2 D.,
8.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.从茂名电白到湛江赤坎全长约为105km,一辆小汽车、一辆货车同时从茂名电白、湛江赤坎两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6km,设小汽车和货车的速度分别为xkm/h,ykm/h,则下列方程组正确的是( )
A. B.
C. D.
10.某学校体育场的环形跑道长250m,甲、乙分别以一定的速度练习长跑和骑自行车,同时同地出发,如果反向而行,那么他们每隔20s相遇一次.如果同向而行,那么每隔50s乙就追上甲一次,设甲的速度为xm/s,乙的速度为ym/s,则可列方程组为( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11. 若a-3b=2,3a-b=6,则b-a的值为__ __.
12. 若是关于x,y的二元一次方程ax+y=3的解,则a=__ _.
13. 试写出一个关于x,y的二元一次方程组,使它的解是 这个方程组可以是________________.
14.已知方程组的解为,则的值为__________.
15.已知是方程3mx﹣y=﹣1的解,则m=_____.
16.若关于的二元一次方程组的解是互为相反数,则的值是_________.
17.欢欢对乐乐说“当我的年龄是你现在年龄时,你才2岁”;乐乐对欢欢说:“当我的年龄是你现在的年龄时,你将23岁”.求两人现在的年龄.设欢欢现在为x岁,乐乐现在年龄为y岁.列出的二元一次方程组是 .(要求所列方程组保留原来的数量关系,不要化简)
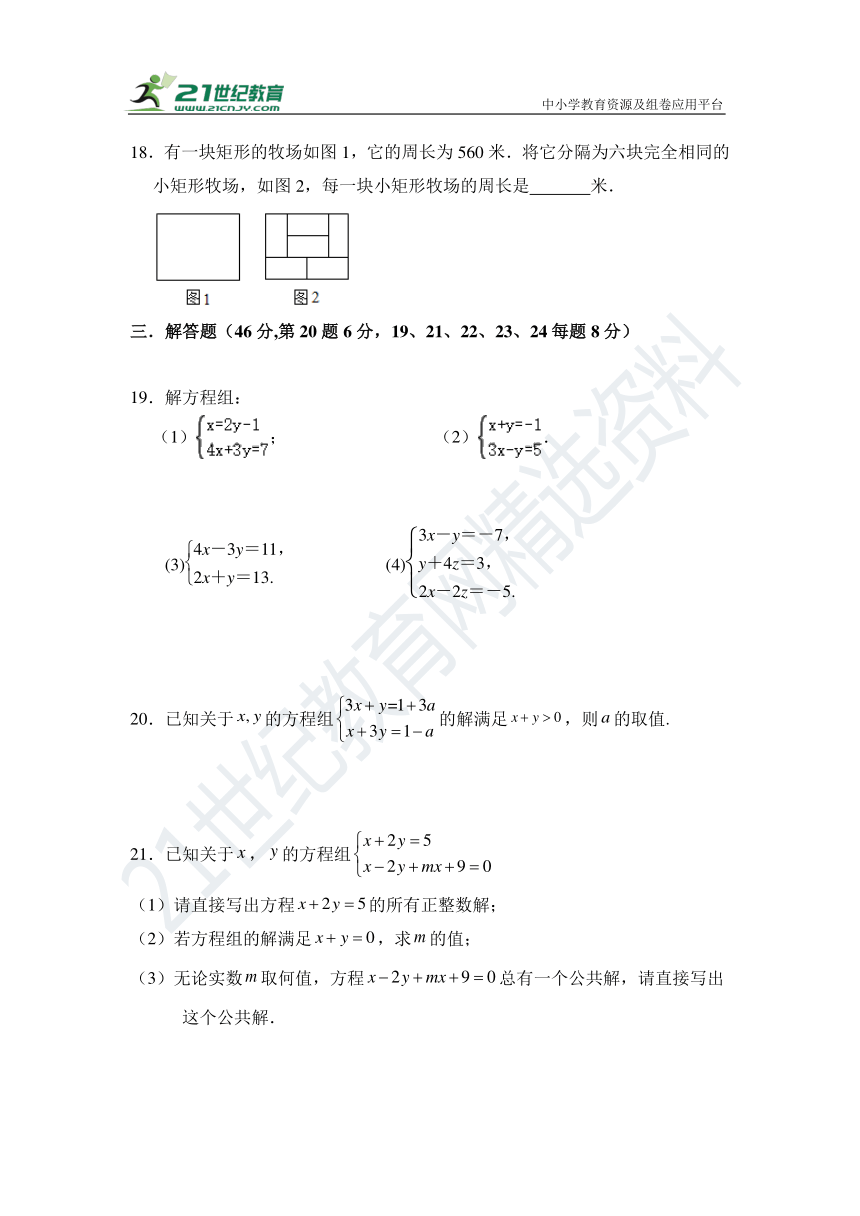
18.有一块矩形的牧场如图1,它的周长为560米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是 米.
三.解答题(46分,第20题6分,19、21、22、23、24每题8分)
19.解方程组:
(1); (2).
(3) (4)
20.已知关于的方程组的解满足,则的取值.
21.已知关于,的方程组
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论实数取何值,方程总有一个公共解,请直接写出这个公共解.
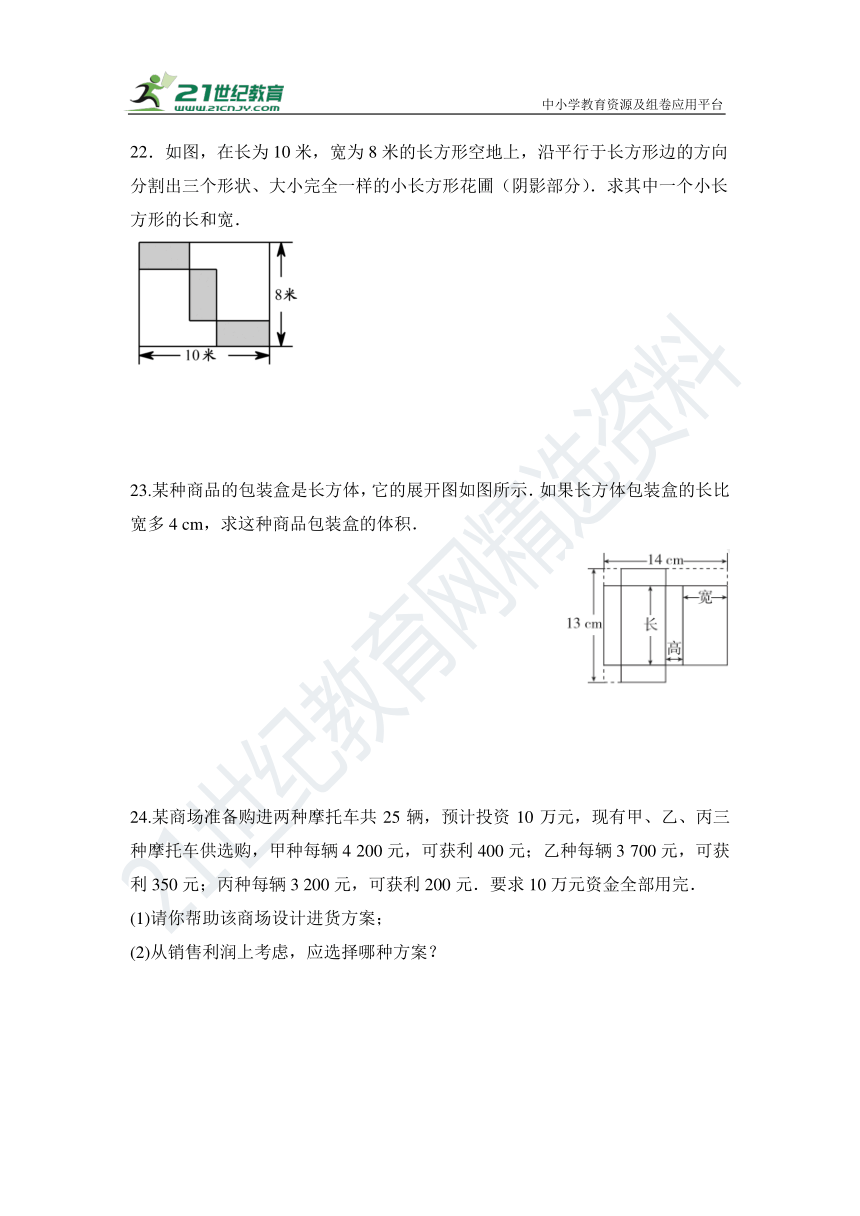
22.如图,在长为10米,宽为8米的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
23.某种商品的包装盒是长方体,它的展开图如图所示.如果长方体包装盒的长比宽多4 cm,求这种商品包装盒的体积.
24.某商场准备购进两种摩托车共25辆,预计投资10万元,现有甲、乙、丙三种摩托车供选购,甲种每辆4 200元,可获利400元;乙种每辆3 700元,可获利350元;丙种每辆3 200元,可获利200元.要求10万元资金全部用完.
(1)请你帮助该商场设计进货方案;
(2)从销售利润上考虑,应选择哪种方案?
【答案】
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C A D B C B A C
二、填空题:
11.解:方程移项,得y=﹣2x+3.
故答案为:y=﹣2x+3.
12.解:根据题意得:|n|=1,m﹣2=1,
解得:n=±1,m=3,
∴m+n=3+1=4,m+n=3﹣1=2,
∴m+n的值是2或4,
故答案为:2或4.
13.解:把代入方程ax﹣y=4,
得2a﹣3=4,
解得a=.
故答案为:.
14.6
15.
16.9
17.解:设甲的速度为xm/s,乙的速度为ym/s,
依题意,得:,
解得:.
故答案为:.
18.解:设鸡有x只,兔有y只,
根据题意,可列方程组为,
故答案是:.
三.解答题
19.解:(1)
,
把①代入②得:4(2y﹣1)+3y=7,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为;
(2)
,
①+②得:4x=4,
解得:x=1,
把x=1代入①得:y=﹣2,
则方程组的解为.
(3)
①+②×3,得10x=50,
解得x=5.
把x=5代入②,
得2×5+y=13,解得y=3.
于是,得方程组的解为
(4)
①+②得3x+4z=-4.④
④+③×2得x=-2.
把x=-2代入①得y=1.
把x=-2代入③得z=.
所以
20.a> 1
21.(1);(2);(3).
22. 8
【解析】
设小长方形的长为 x 米,宽为y米. 依题意有:解方程组即可.
解: 设小长方形的长为 x 米,宽为y米.
依题意有:
解此方程组得:
故,小长方形的长为 4米,宽为2米.
【点睛】
本题考核知识点:列方程组解应用题.解题关键点:根据已知列出方程组.
23. 解:设这种商品包装盒的宽为x cm,高为y cm,则长为(x+4)cm.根据题意,得解得所以x+4=9,故这种商品包装盒的长为9 cm,宽为5 cm,高为2 cm,所以其体积为9×5×2=90(cm3).答:这种商品包装盒的体积为90 cm3.
24. 解:(1)有三种方案:第一种购甲、乙两种摩托,设购进甲种摩托车为x辆,乙种摩托车为y辆,则解得
第二种购甲、丙两种摩托,设购进甲种摩托车为x辆,丙种摩托车为y辆,则解得
第三种购乙、丙两种摩托,设购进乙种摩托车为x辆,丙种摩托车为y辆,则解得∵x,y均为正整数,∴这种方案不成立,∴只有两种方案.
(2)第一种方案赢利400×15+350×10=9 500(元),第二种方案赢利400×20+200×5=9 000(元).∴选择第一种方案.
第八章《二元一次方程组》单元检测题
一、选择题(每题3分,共30分)
1.下面各组数值中,二元一次方程2x+y=10的解是( )
A. B. C. D.
2.解方程组 的最好解法是( )
A.由①得y=3x﹣2,再代入② B.由②得3x=11﹣2y,再代入①
C.由①×2+②消去y D.由②﹣①,消去x
3.已知 是方程 的一组解,那么m的值是( )
4.二元一次方程3x+y=8的正整数解有( )
A.2个 B.3个 C.4个 D.5个
5.若二元一次方程3x﹣y=7,3x+5y=1,y=kx﹣9有公共解,则k的取值为( )
A.5 B.﹣3 C.﹣4 D.4
6.若关于x,y的方程组的解互为相反数,则m的值等于( )
A.1 B.0 C.﹣1 D.2
7.若和是方程的两组解,则m,n的值分别为( )
A., B.2,4 C.4,2 D.,
8.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.从茂名电白到湛江赤坎全长约为105km,一辆小汽车、一辆货车同时从茂名电白、湛江赤坎两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6km,设小汽车和货车的速度分别为xkm/h,ykm/h,则下列方程组正确的是( )
A. B.
C. D.
10.某学校体育场的环形跑道长250m,甲、乙分别以一定的速度练习长跑和骑自行车,同时同地出发,如果反向而行,那么他们每隔20s相遇一次.如果同向而行,那么每隔50s乙就追上甲一次,设甲的速度为xm/s,乙的速度为ym/s,则可列方程组为( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11. 若a-3b=2,3a-b=6,则b-a的值为__ __.
12. 若是关于x,y的二元一次方程ax+y=3的解,则a=__ _.
13. 试写出一个关于x,y的二元一次方程组,使它的解是 这个方程组可以是________________.
14.已知方程组的解为,则的值为__________.
15.已知是方程3mx﹣y=﹣1的解,则m=_____.
16.若关于的二元一次方程组的解是互为相反数,则的值是_________.
17.欢欢对乐乐说“当我的年龄是你现在年龄时,你才2岁”;乐乐对欢欢说:“当我的年龄是你现在的年龄时,你将23岁”.求两人现在的年龄.设欢欢现在为x岁,乐乐现在年龄为y岁.列出的二元一次方程组是 .(要求所列方程组保留原来的数量关系,不要化简)
18.有一块矩形的牧场如图1,它的周长为560米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是 米.
三.解答题(46分,第20题6分,19、21、22、23、24每题8分)
19.解方程组:
(1); (2).
(3) (4)
20.已知关于的方程组的解满足,则的取值.
21.已知关于,的方程组
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论实数取何值,方程总有一个公共解,请直接写出这个公共解.
22.如图,在长为10米,宽为8米的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
23.某种商品的包装盒是长方体,它的展开图如图所示.如果长方体包装盒的长比宽多4 cm,求这种商品包装盒的体积.
24.某商场准备购进两种摩托车共25辆,预计投资10万元,现有甲、乙、丙三种摩托车供选购,甲种每辆4 200元,可获利400元;乙种每辆3 700元,可获利350元;丙种每辆3 200元,可获利200元.要求10万元资金全部用完.
(1)请你帮助该商场设计进货方案;
(2)从销售利润上考虑,应选择哪种方案?
【答案】
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C A D B C B A C
二、填空题:
11.解:方程移项,得y=﹣2x+3.
故答案为:y=﹣2x+3.
12.解:根据题意得:|n|=1,m﹣2=1,
解得:n=±1,m=3,
∴m+n=3+1=4,m+n=3﹣1=2,
∴m+n的值是2或4,
故答案为:2或4.
13.解:把代入方程ax﹣y=4,
得2a﹣3=4,
解得a=.
故答案为:.
14.6
15.
16.9
17.解:设甲的速度为xm/s,乙的速度为ym/s,
依题意,得:,
解得:.
故答案为:.
18.解:设鸡有x只,兔有y只,
根据题意,可列方程组为,
故答案是:.
三.解答题
19.解:(1)
,
把①代入②得:4(2y﹣1)+3y=7,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为;
(2)
,
①+②得:4x=4,
解得:x=1,
把x=1代入①得:y=﹣2,
则方程组的解为.
(3)
①+②×3,得10x=50,
解得x=5.
把x=5代入②,
得2×5+y=13,解得y=3.
于是,得方程组的解为
(4)
①+②得3x+4z=-4.④
④+③×2得x=-2.
把x=-2代入①得y=1.
把x=-2代入③得z=.
所以
20.a> 1
21.(1);(2);(3).
22. 8
【解析】
设小长方形的长为 x 米,宽为y米. 依题意有:解方程组即可.
解: 设小长方形的长为 x 米,宽为y米.
依题意有:
解此方程组得:
故,小长方形的长为 4米,宽为2米.
【点睛】
本题考核知识点:列方程组解应用题.解题关键点:根据已知列出方程组.
23. 解:设这种商品包装盒的宽为x cm,高为y cm,则长为(x+4)cm.根据题意,得解得所以x+4=9,故这种商品包装盒的长为9 cm,宽为5 cm,高为2 cm,所以其体积为9×5×2=90(cm3).答:这种商品包装盒的体积为90 cm3.
24. 解:(1)有三种方案:第一种购甲、乙两种摩托,设购进甲种摩托车为x辆,乙种摩托车为y辆,则解得
第二种购甲、丙两种摩托,设购进甲种摩托车为x辆,丙种摩托车为y辆,则解得
第三种购乙、丙两种摩托,设购进乙种摩托车为x辆,丙种摩托车为y辆,则解得∵x,y均为正整数,∴这种方案不成立,∴只有两种方案.
(2)第一种方案赢利400×15+350×10=9 500(元),第二种方案赢利400×20+200×5=9 000(元).∴选择第一种方案.
