第十九章 一次函数单元同步检测试题(含答案)
文档属性
| 名称 | 第十九章 一次函数单元同步检测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 12:07:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.下列函数中,y随x的增大而减小的有( )
①y=﹣2x+1;②y=6﹣x;③y=;④y=(1﹣)x.
A.1个 B.2个 C.3个 D.4个
2.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是( )
A. B. C. D.
3.对于一次函数y=2x+4,下列结论正确的是( )
A.函数值随自变量的增大而减小
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得y=﹣2x的图象
D.函数的图象与y轴的交点坐标是(0,4)
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5. 如果每盒羽毛球有20个,每盒售价为24元,那么羽毛球的售价(元)与羽毛球个数(个)之间的关系式为( )
A. B.
C. D.
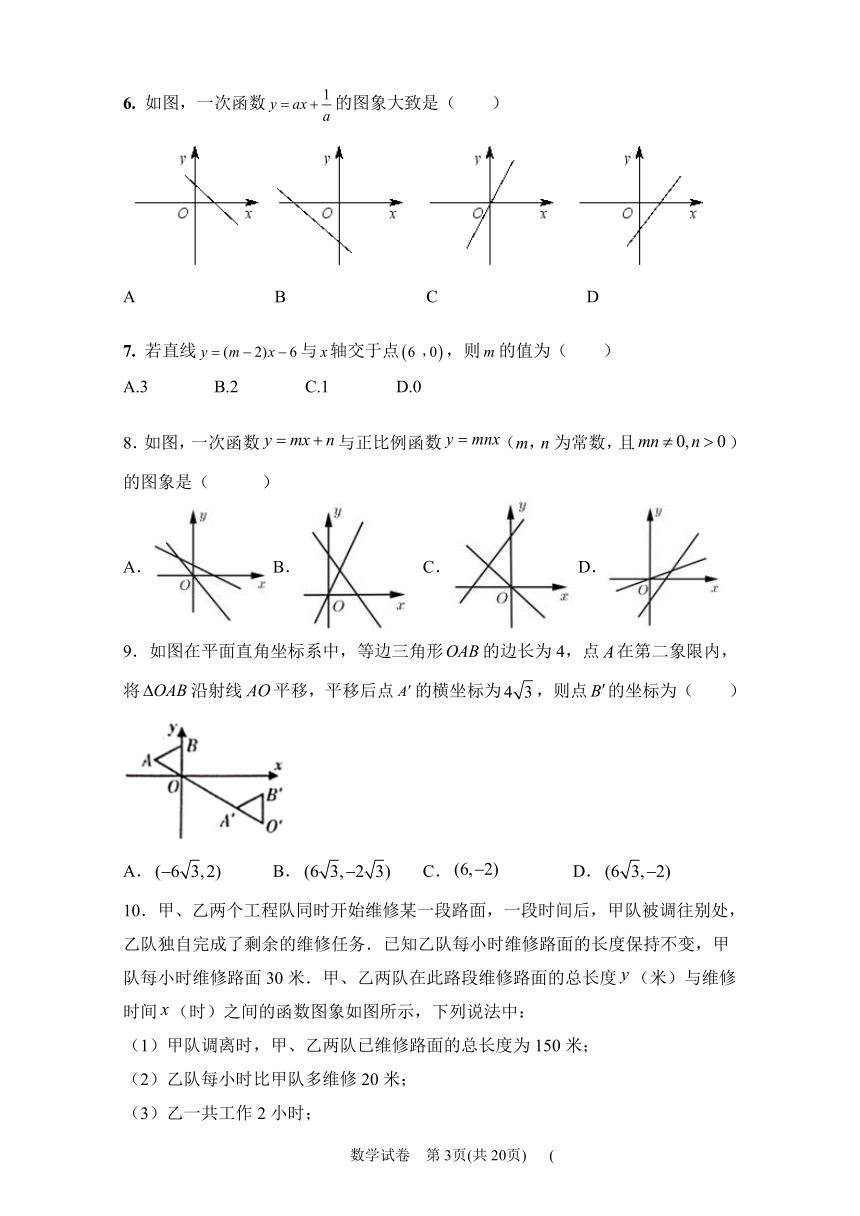
6. 如图,一次函数的图象大致是( )
A B C D
7. 若直线与轴交于点,则的值为( )
A.3 B.2 C.1 D.0
8.如图,一次函数与正比例函数(m,n为常数,且)的图象是( )
A. B. C. D.
9.如图在平面直角坐标系中,等边三角形的边长为4,点在第二象限内,将沿射线平移,平移后点的横坐标为,则点的坐标为( )
A. B. C. D.
10.甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队独自完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度(米)与维修时间(时)之间的函数图象如图所示,下列说法中:
(1)甲队调离时,甲、乙两队已维修路面的总长度为150米;
(2)乙队每小时比甲队多维修20米;
(3)乙一共工作2小时;
(4).
正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题(每题3分,共30分)
11.函数中自变量x的取值范围是________.
12.已知 ,与成正比例,与成反比例,且当x=1时,y=-1,当x=3时,y=5,求y与x之间的函数关系式_______________.
13.已知一次函数的图象经过第一、二、三象限,则b的取值范围是___________.
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17. 如图所示的是函数与的图象,求方程组 的解关于原点对称的点的坐标是________.
18. 已知,是方程组的解,那么一次函数________和________的交点是________.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知一次函数y=(4m+1)x﹣(m+1).
(1)m为何值时,y随x的增大而减小?
(2)m为何值时,直线与y轴的交点在x轴下方?
(3)m为何值时,直线位于第二、三、四象限?
20.如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6,相应函数值是﹣11≤y≤9,求此函数解析式.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.甲、已两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按折出售,乙商场对一次购物中超过200元后的价格部分打折. 设原价购物金额累计为元().
根据题意,填写下表: (单位:元)
原价购物金额累计/元. 130 300 700 ···
甲商场实际购物金额/元 104 560 ···
乙商场实际购物金额/元 130 270 ···
设在甲商场实际购物金额为元,在乙商场实际购物金额为元,分别写出,关于的函数解析式;
根据题意填空:
①若在同甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为______元 ;
②若在同一商场购物,商品原价购物金额累计为 元,则在甲、乙.两家商场中的 商场实际购物花费金少.
③若在同一商场实际购物金额为元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
24.某市地铁1号线全长约60km,市政府通过招标,甲、乙两家地铁工程公司承担了施工任务,根据招标合同可知,甲公司每月计划施工效率是乙公司的1.2倍,则乙公司单独施工比甲公司单独施工多用10个月,且市政府需要支付给甲公司的施工费用为6亿元/km,乙公司的施工费用为5亿元/km.
(1)甲、乙两家地铁工程公司每月计划施工各为多少km?
(2)由于设备和施工现场只能供一家地铁工程公司单独施工的原因,现计划甲、乙两家公司共用55个月恰好完成施工任务(每家公司施工时间不足一个月按照一个整月计算),且甲公司施工时间不得少于乙公司的两倍,应如何安排才能使市政府支付给两家地铁工程公司的总费用最少?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D D A C B C A
二、填空题(每题3分,共24分)
11.且
,
根据题意得:x≥0 ,,
解得:且.
故答案为:且.
12.
由题意设
则
将时,和时,代入得:
解得:
故与之间的函数关系为.
故答案为:.
13.b>0
解:如图,已知一次函数经过一、二、三象限,
∴k>0,b>0
∵k=2>0
∴只需b>0
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知一次函数y=(4m+1)x﹣(m+1).
(1)m为何值时,y随x的增大而减小?
(2)m为何值时,直线与y轴的交点在x轴下方?
(3)m为何值时,直线位于第二、三、四象限?
【考点】一次函数的性质;不等式的性质;解一元一次不等式;解一元一次不等式组.版权所有
【专题】计算题.
【分析】(1)根据一次函数的性质得出不等式4m+1<0,求出不等式的解集即可;
(2)根据一次函数的性质得出不等式﹣(m+1)<0,求出不等式的解集即可;
(3)根据一次函数的性质得出不等式4m+1<0和﹣(m+1)<0,求出不等式组的解集即可.
【解答】解:(1)一次函数y=(4m+1)x﹣(m+1),
∵y随x的增大而减小,
∴4m+1<0,
解得:m<﹣,
答:当m<﹣时,y随x的增大而减小.
(2)一次函数y=(4m+1)x﹣(m+1),
∵直线与y轴的交点在x轴下方,
∴﹣(m+1)<0,
解得:m>﹣1,且m≠﹣,
答:当m>﹣1且m≠﹣时,直线与y轴的交点在x轴下方.
(3)一次函数y=(4m+1)x﹣(m+1),
∵直线位于第二、三、四象限,
∴4m+1<0且﹣(m+1)<0,
解得:﹣1<m<﹣,
答:当:﹣1<m<﹣时,直线位于第二、三、四象限.
【点评】本题主要考查对解一元一次不等式(组),不等式的性质,一次函数的性质等知识点的理解和掌握,能熟练地根据一次函数的性质和已知得出不等式是解此题的关键.
20.如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6,相应函数值是﹣11≤y≤9,求此函数解析式.
【考点】待定系数法求一次函数解析式.版权所有
【专题】分类讨论;待定系数法.
【分析】因为函数增减性不明确,所以分①k>0时,函数值随x的增大而增大,此时当x=﹣2时,y=﹣11,x=6时,y=9;
②k<0时,函数值随x增大而减小,此时当x=﹣2时,y=9,x=6时,y=﹣11;两种情况讨论.
【解答】解:根据题意,①当k>0时,y随x增大而增大,
∴当x=﹣2时,y=﹣11,x=6时,y=9
∴解得,
∴函数解析式为y=x﹣6;
②当k<0时,函数值随x增大而减小,
∴当x=﹣2时,y=9,x=6时,y=﹣11,
∴解得,
∴函数解析式为y=﹣x+4.
因此,函数解析式为y=x﹣6或y=﹣x+4.
【点评】本题主要考查一次函数的性质,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小,注意要分情况讨论.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.(1)240,550;(2) ,,; (3) ①,②乙;③甲
24.(1)甲公司每月计划施工1.2km,乙公司每月施工1km;(2)甲公司施工37个月,乙公司施工18个月,总费用最少
数学试卷 第19页(共22页) ( 数学试卷 第20页(共22页)
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.下列函数中,y随x的增大而减小的有( )
①y=﹣2x+1;②y=6﹣x;③y=;④y=(1﹣)x.
A.1个 B.2个 C.3个 D.4个
2.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是( )
A. B. C. D.
3.对于一次函数y=2x+4,下列结论正确的是( )
A.函数值随自变量的增大而减小
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得y=﹣2x的图象
D.函数的图象与y轴的交点坐标是(0,4)
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5. 如果每盒羽毛球有20个,每盒售价为24元,那么羽毛球的售价(元)与羽毛球个数(个)之间的关系式为( )
A. B.
C. D.
6. 如图,一次函数的图象大致是( )
A B C D
7. 若直线与轴交于点,则的值为( )
A.3 B.2 C.1 D.0
8.如图,一次函数与正比例函数(m,n为常数,且)的图象是( )
A. B. C. D.
9.如图在平面直角坐标系中,等边三角形的边长为4,点在第二象限内,将沿射线平移,平移后点的横坐标为,则点的坐标为( )
A. B. C. D.
10.甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队独自完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度(米)与维修时间(时)之间的函数图象如图所示,下列说法中:
(1)甲队调离时,甲、乙两队已维修路面的总长度为150米;
(2)乙队每小时比甲队多维修20米;
(3)乙一共工作2小时;
(4).
正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题(每题3分,共30分)
11.函数中自变量x的取值范围是________.
12.已知 ,与成正比例,与成反比例,且当x=1时,y=-1,当x=3时,y=5,求y与x之间的函数关系式_______________.
13.已知一次函数的图象经过第一、二、三象限,则b的取值范围是___________.
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17. 如图所示的是函数与的图象,求方程组 的解关于原点对称的点的坐标是________.
18. 已知,是方程组的解,那么一次函数________和________的交点是________.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知一次函数y=(4m+1)x﹣(m+1).
(1)m为何值时,y随x的增大而减小?
(2)m为何值时,直线与y轴的交点在x轴下方?
(3)m为何值时,直线位于第二、三、四象限?
20.如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6,相应函数值是﹣11≤y≤9,求此函数解析式.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.甲、已两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按折出售,乙商场对一次购物中超过200元后的价格部分打折. 设原价购物金额累计为元().
根据题意,填写下表: (单位:元)
原价购物金额累计/元. 130 300 700 ···
甲商场实际购物金额/元 104 560 ···
乙商场实际购物金额/元 130 270 ···
设在甲商场实际购物金额为元,在乙商场实际购物金额为元,分别写出,关于的函数解析式;
根据题意填空:
①若在同甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为______元 ;
②若在同一商场购物,商品原价购物金额累计为 元,则在甲、乙.两家商场中的 商场实际购物花费金少.
③若在同一商场实际购物金额为元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
24.某市地铁1号线全长约60km,市政府通过招标,甲、乙两家地铁工程公司承担了施工任务,根据招标合同可知,甲公司每月计划施工效率是乙公司的1.2倍,则乙公司单独施工比甲公司单独施工多用10个月,且市政府需要支付给甲公司的施工费用为6亿元/km,乙公司的施工费用为5亿元/km.
(1)甲、乙两家地铁工程公司每月计划施工各为多少km?
(2)由于设备和施工现场只能供一家地铁工程公司单独施工的原因,现计划甲、乙两家公司共用55个月恰好完成施工任务(每家公司施工时间不足一个月按照一个整月计算),且甲公司施工时间不得少于乙公司的两倍,应如何安排才能使市政府支付给两家地铁工程公司的总费用最少?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D D A C B C A
二、填空题(每题3分,共24分)
11.且
,
根据题意得:x≥0 ,,
解得:且.
故答案为:且.
12.
由题意设
则
将时,和时,代入得:
解得:
故与之间的函数关系为.
故答案为:.
13.b>0
解:如图,已知一次函数经过一、二、三象限,
∴k>0,b>0
∵k=2>0
∴只需b>0
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知一次函数y=(4m+1)x﹣(m+1).
(1)m为何值时,y随x的增大而减小?
(2)m为何值时,直线与y轴的交点在x轴下方?
(3)m为何值时,直线位于第二、三、四象限?
【考点】一次函数的性质;不等式的性质;解一元一次不等式;解一元一次不等式组.版权所有
【专题】计算题.
【分析】(1)根据一次函数的性质得出不等式4m+1<0,求出不等式的解集即可;
(2)根据一次函数的性质得出不等式﹣(m+1)<0,求出不等式的解集即可;
(3)根据一次函数的性质得出不等式4m+1<0和﹣(m+1)<0,求出不等式组的解集即可.
【解答】解:(1)一次函数y=(4m+1)x﹣(m+1),
∵y随x的增大而减小,
∴4m+1<0,
解得:m<﹣,
答:当m<﹣时,y随x的增大而减小.
(2)一次函数y=(4m+1)x﹣(m+1),
∵直线与y轴的交点在x轴下方,
∴﹣(m+1)<0,
解得:m>﹣1,且m≠﹣,
答:当m>﹣1且m≠﹣时,直线与y轴的交点在x轴下方.
(3)一次函数y=(4m+1)x﹣(m+1),
∵直线位于第二、三、四象限,
∴4m+1<0且﹣(m+1)<0,
解得:﹣1<m<﹣,
答:当:﹣1<m<﹣时,直线位于第二、三、四象限.
【点评】本题主要考查对解一元一次不等式(组),不等式的性质,一次函数的性质等知识点的理解和掌握,能熟练地根据一次函数的性质和已知得出不等式是解此题的关键.
20.如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6,相应函数值是﹣11≤y≤9,求此函数解析式.
【考点】待定系数法求一次函数解析式.版权所有
【专题】分类讨论;待定系数法.
【分析】因为函数增减性不明确,所以分①k>0时,函数值随x的增大而增大,此时当x=﹣2时,y=﹣11,x=6时,y=9;
②k<0时,函数值随x增大而减小,此时当x=﹣2时,y=9,x=6时,y=﹣11;两种情况讨论.
【解答】解:根据题意,①当k>0时,y随x增大而增大,
∴当x=﹣2时,y=﹣11,x=6时,y=9
∴解得,
∴函数解析式为y=x﹣6;
②当k<0时,函数值随x增大而减小,
∴当x=﹣2时,y=9,x=6时,y=﹣11,
∴解得,
∴函数解析式为y=﹣x+4.
因此,函数解析式为y=x﹣6或y=﹣x+4.
【点评】本题主要考查一次函数的性质,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小,注意要分情况讨论.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23.(1)240,550;(2) ,,; (3) ①,②乙;③甲
24.(1)甲公司每月计划施工1.2km,乙公司每月施工1km;(2)甲公司施工37个月,乙公司施工18个月,总费用最少
数学试卷 第19页(共22页) ( 数学试卷 第20页(共22页)
