4.3 探索三角形全等的条件 课件(共19张PPT) 2023-2024学年北师大版七年级数学下册
文档属性
| 名称 | 4.3 探索三角形全等的条件 课件(共19张PPT) 2023-2024学年北师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 151.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
4.3探索三角形全等的条件
主讲人:###
三角形全等的性质与判定条件
01
02
03
04
05
三角形全等的性质
三角形全等判定——SSS
三角形全等判定——SAS
三角形全等判定——AAS
三角形全等判定——SAS
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
三角形全等的定义:
[ 能够完全重合的两个三角形称为全等三角形 ]
两个三角形全等的性质:
(1)全等三角形的形状和大小都相同
(2)全等三角形的对应边,对应角相等
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
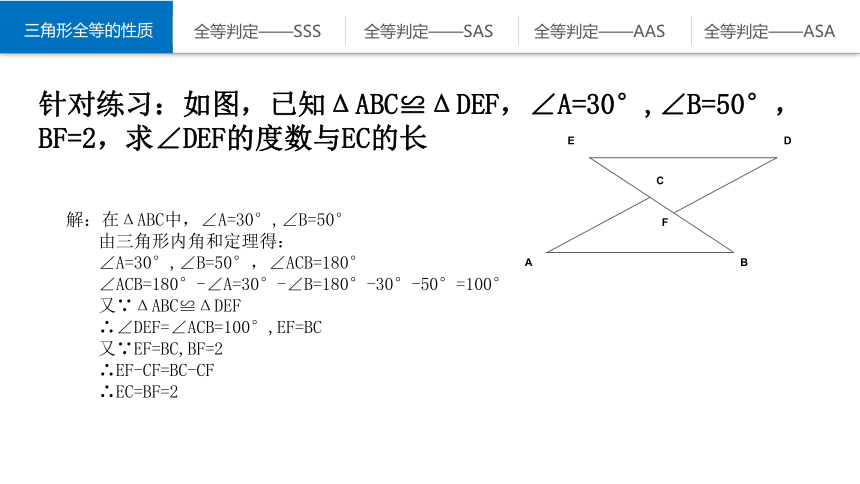
针对练习:如图,已知ΔABC≌ΔDEF,∠A=30°,∠B=50°,
BF=2,求∠DEF的度数与EC的长
A
B
F
C
E
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知ΔABC≌ΔDEF,∠A=30°,∠B=50°,
BF=2,求∠DEF的度数与EC的长
解:在ΔABC中,∠A=30°,∠B=50°
由三角形内角和定理得:
∠A=30°,∠B=50°,∠ACB=180°
∠ACB=180°-∠A=30°-∠B=180°-30°-50°=100°
又∵ΔABC≌ΔDEF
∴∠DEF=∠ACB=100°,EF=BC
又∵EF=BC,BF=2
∴EF-CF=BC-CF
∴EC=BF=2
A
B
F
C
E
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法一:
三边分别相等的两个三角形全等【三角形具有稳定性】
( 简写为“边边边”或“SSS”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
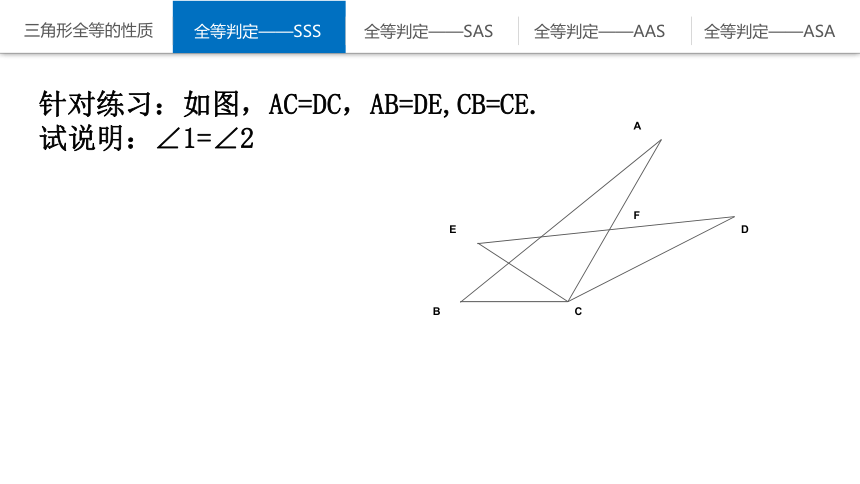
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
B
A
E
C
F
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
解:∠1=∠2,理由如下:
在ΔABC与ΔDEC中
AC=DC
AB=DE
CB=CE
∴ΔABC≌ΔDEC
∴∠A=∠D
由三角形内角和定理得:
∠1+∠A+∠AFE=180°
∠2+∠D+∠DFC=180°
又∵∠A=∠D,∠AFE=∠DFC(对顶角相等)
∴∠1=∠2
B
A
E
C
F
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法二:
两边及其夹角分别相等的两个三角形全等
( 简写成“边角边”或“SAS”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD,
试说明:ΔAOB≌ΔCOD
O
D
C
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD,
试说明:ΔAOB≌ΔCOD
解:ΔAOB≌ΔCOD,理由如下:
∴∠AOC=∠BOD
∴∠AOC-∠AOD=∠BOD-∠AOD
∴∠COD=∠AOB
在ΔAOB与ΔCOD中
OA=OC
∠COD=∠AOB
OB=OD
∴ΔAOB≌ΔCOD
O
D
C
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法三:
两角分别相等且其中一组等角的对边相等的两个三角形全等
( 简写成“角角边”或“AAS”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,D是AC上一点,AE=BC,DE//AB,
∠B=∠DAE,试说明:ΔABC≌ΔDAE
E
C
D
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,D是AC上一点,AE=BC,DE//AB,
∠B=∠DAE,试说明:ΔABC≌ΔDAE
解:ΔABC≌ΔDAE,理由如下:
∵DE//AB
∴∠ADE=∠BAC
在ΔABC与ΔDAE中
∠ADE=∠BAC
∠B=∠DAE
AE=BC
∴ΔABC≌ΔDAE
E
C
D
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法四:
两角及其夹边分别相等的两个三角形全等
( 简写成“边角边”或“ASA”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE,
试说明:BD=CE
B
A
D
E
C
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE,
试说明:BD=CE
解:ΔAOB≌ΔCOD,理由如下:
∵AB⊥AC,AD⊥AE
∴∠DAE=∠BAC
∴∠DAE-∠BAE=∠BAC-∠BAE
∴∠DAB=∠EAC
在ΔABD与ΔACE中
∠DAB=∠EAC
AB=AC
∠ABD=∠ACE
∴ΔABD≌ΔACE
∴BD=CE
B
A
D
E
C
01
02
03
04
三角形全等判定——SSS
三角形全等判定——SAS
三角形全等判定——AAS
三角形全等判定——SAS
三角形全等的判定条件
反思总结
判定两个三角形全等的思路:
(1)已知两边对应相等判定两个三角形全等,有“SAS”“SSS”,所以可以从两个方面进行考虑.
(2)已知两角对应相等判定两个三角形全等有“ASA”“AAS”,所以可以从两个方面进行考虑.
(3)已知一边与其对角对应相等,与之相对应的判定只有“AAS”,所以只能从这个方面进行考虑.
(4)已知一边及与其相邻的一个内角对应相等,判定两个三角形全等,有“SAS”“ASA”“AAS”,所以可以从三个方面进行考虑.
4.3探索三角形全等的条件
主讲人:###
三角形全等的性质与判定条件
01
02
03
04
05
三角形全等的性质
三角形全等判定——SSS
三角形全等判定——SAS
三角形全等判定——AAS
三角形全等判定——SAS
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
三角形全等的定义:
[ 能够完全重合的两个三角形称为全等三角形 ]
两个三角形全等的性质:
(1)全等三角形的形状和大小都相同
(2)全等三角形的对应边,对应角相等
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知ΔABC≌ΔDEF,∠A=30°,∠B=50°,
BF=2,求∠DEF的度数与EC的长
A
B
F
C
E
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知ΔABC≌ΔDEF,∠A=30°,∠B=50°,
BF=2,求∠DEF的度数与EC的长
解:在ΔABC中,∠A=30°,∠B=50°
由三角形内角和定理得:
∠A=30°,∠B=50°,∠ACB=180°
∠ACB=180°-∠A=30°-∠B=180°-30°-50°=100°
又∵ΔABC≌ΔDEF
∴∠DEF=∠ACB=100°,EF=BC
又∵EF=BC,BF=2
∴EF-CF=BC-CF
∴EC=BF=2
A
B
F
C
E
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法一:
三边分别相等的两个三角形全等【三角形具有稳定性】
( 简写为“边边边”或“SSS”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
B
A
E
C
F
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
解:∠1=∠2,理由如下:
在ΔABC与ΔDEC中
AC=DC
AB=DE
CB=CE
∴ΔABC≌ΔDEC
∴∠A=∠D
由三角形内角和定理得:
∠1+∠A+∠AFE=180°
∠2+∠D+∠DFC=180°
又∵∠A=∠D,∠AFE=∠DFC(对顶角相等)
∴∠1=∠2
B
A
E
C
F
D
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法二:
两边及其夹角分别相等的两个三角形全等
( 简写成“边角边”或“SAS”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD,
试说明:ΔAOB≌ΔCOD
O
D
C
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD,
试说明:ΔAOB≌ΔCOD
解:ΔAOB≌ΔCOD,理由如下:
∴∠AOC=∠BOD
∴∠AOC-∠AOD=∠BOD-∠AOD
∴∠COD=∠AOB
在ΔAOB与ΔCOD中
OA=OC
∠COD=∠AOB
OB=OD
∴ΔAOB≌ΔCOD
O
D
C
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法三:
两角分别相等且其中一组等角的对边相等的两个三角形全等
( 简写成“角角边”或“AAS”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,D是AC上一点,AE=BC,DE//AB,
∠B=∠DAE,试说明:ΔABC≌ΔDAE
E
C
D
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,D是AC上一点,AE=BC,DE//AB,
∠B=∠DAE,试说明:ΔABC≌ΔDAE
解:ΔABC≌ΔDAE,理由如下:
∵DE//AB
∴∠ADE=∠BAC
在ΔABC与ΔDAE中
∠ADE=∠BAC
∠B=∠DAE
AE=BC
∴ΔABC≌ΔDAE
E
C
D
A
B
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
判定方法四:
两角及其夹边分别相等的两个三角形全等
( 简写成“边角边”或“ASA”)
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE,
试说明:BD=CE
B
A
D
E
C
选题背景
全等判定——AAS
三角形全等的性质
全等判定——SAS
全等判定——SSS
全等判定——ASA
针对练习:如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE,
试说明:BD=CE
解:ΔAOB≌ΔCOD,理由如下:
∵AB⊥AC,AD⊥AE
∴∠DAE=∠BAC
∴∠DAE-∠BAE=∠BAC-∠BAE
∴∠DAB=∠EAC
在ΔABD与ΔACE中
∠DAB=∠EAC
AB=AC
∠ABD=∠ACE
∴ΔABD≌ΔACE
∴BD=CE
B
A
D
E
C
01
02
03
04
三角形全等判定——SSS
三角形全等判定——SAS
三角形全等判定——AAS
三角形全等判定——SAS
三角形全等的判定条件
反思总结
判定两个三角形全等的思路:
(1)已知两边对应相等判定两个三角形全等,有“SAS”“SSS”,所以可以从两个方面进行考虑.
(2)已知两角对应相等判定两个三角形全等有“ASA”“AAS”,所以可以从两个方面进行考虑.
(3)已知一边与其对角对应相等,与之相对应的判定只有“AAS”,所以只能从这个方面进行考虑.
(4)已知一边及与其相邻的一个内角对应相等,判定两个三角形全等,有“SAS”“ASA”“AAS”,所以可以从三个方面进行考虑.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
