人教版七年级数学上册第二章《整式的加减》单元复习课件
文档属性
| 名称 | 人教版七年级数学上册第二章《整式的加减》单元复习课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-22 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
第二章 《整式的加减》复习
人教版七年级数学上册
教学目标
1.教学目标
(1)梳理整式的相关概念,通过回顾单项式、多项式、整式及有关的概念,归纳概念之间的区别与联系;
(2)在正确合并同类项、准确运用去括号时的符号变化规律的基础上,达到可以熟练地进行整式的加减运算;
(3)通过分析实际问题中的数量关系,进一步体会用字母表示数的意义,通过对数与式运算的分析,体会“数式通性”,体会蕴含在具体问题中的数学思想和规律,以及数学知识之间“具体”与“抽象”的内在联系和数学的内在统一性.
目标解析
2.目标解析
达成目标(1)的标志:清晰地知道单项式、多项式、整式的概念,理解单项式的系数、次数,多项式的项、次数等,可以建立概念之间的联系;
达成目标(2)的标志:更加清晰地认识到进行整式的加减实际上就是将整式化简,化简的主要方法是合并多项式中的同类项和去括号,并体会整式的运算在解决有关计算问题中的作用;
目标(3)是“内容所蕴含的思想方法”,利用所熟悉的数的运算来学习式的运算,充分利用类比的思想方法,是贯穿于全章的重要的思想方法,感悟“数式通性”,并迁移到解决相关的问题之中,需要不断地在应用中提高认识水平.
复习导航
1.举出一些用单项式、多项式表示数量关系的实例.
2 .合并同类项和去括号是整式加减的基础,举例说明合并同类项和去括号的依据?
3.举例说明整式加减的运算法则.
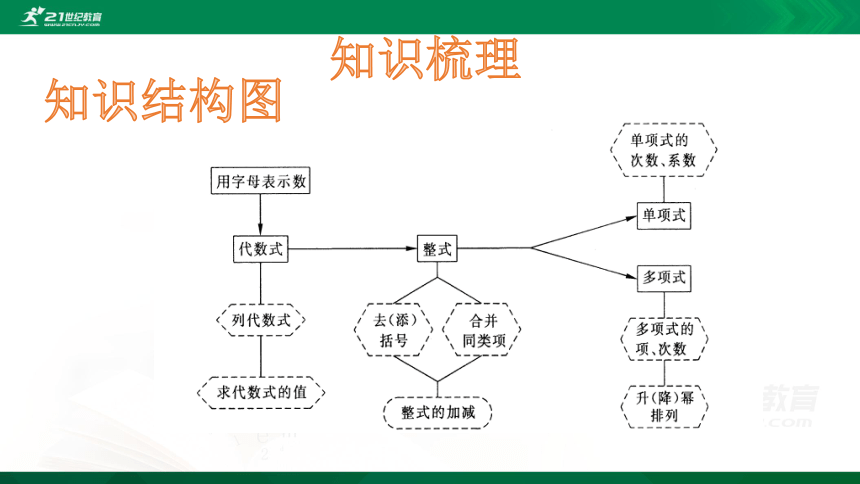
知识梳理
知识结构图
一、整式的相关概念
1.单项式:
由数字或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
要点诠释:(1)单项式的系数是指单项式中的数字因数.
(2)单项式的次数是指单项式中所有字母的指数和.
2.多项式:
几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
要点诠释:(1)在多项式中,不含字母的项叫做常数项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
知识梳理
一、整式的相关概念
3. 多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
要点诠释:
(1)利用加法交换律重新排列时,各项应带着它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
4.整式:
单项式和多项式统称为整式.
知识梳理
二、整式的加减
1.同类项:
所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.
要点诠释:辨别同类项要把准“两相同,两无关”:
(1)“两相同”是指:①所含字母相同;②相同字母的指数相同;
(2)“两无关”是指:①与系数无关;②与字母的排列顺序无关.
2.合并同类项:
把多项式中的同类项合并成一项,叫做合并同类项.
要点诠释:合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.
知识梳理
一、整式的相关概念
3.去括号法则:
括号前面是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前面是“-”,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
4.添括号法则:
添括号后,括号前面是“+”,括号内各项的符号都不改变;添括号后,括号前面是“-”,括号内各项的符号都要改变.
知识梳理
5.整式的加减运算法则:
几个整式相加减,通常用括号把每一个整式括起来,再用加、减号连接,然后去括号,合并同类项.
典例解析
【例1】指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.
【考点】整式.
(1) a-3 (2) 5 (3) (4)
(5) 3xy (6) (7)
【分析】①分母中出现字母的式子不是整式,故 不是整式;
②π是常数而不是字母,故 是整式,也是单项式;
③(7)表示的是加、减关系而不是乘积关系,而单项式中不能有加减.
如 其实质为 .
典例解析
【例1】指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.
(1) a-3 (2) 5 (3) (4)
(5) 3xy (6) (7)
【解答】解:整式:(1)、(2)、(4)、(5)、(6)、(7)
单项式:(2)、(5)、(6),
其中:5的系数是5,次数是0;3xy的系数是3,次数是2; 的系数是 次数是1,多项式(1)、(4)、(7)且它们都是一次二项式.
典例解析
【例2】合并同类项.
【分析】同类项的定义中强调,除所含字母相同外,相同字母的指数也要相同.其中,常数项也是同类项.
合并同类项时,若不是同类项,则不需合并.
解:原式
解:原式
典例解析
【例3】计算:
【分析】根据多重括号的去括号法则,可由里向外,也可由外向里逐层推进,在计算过程中要注意符号的变化.若括号前是“-”号,在去括号时,括号里各项都应变号,若括号前有数字因数,应把数字因数乘到括号里,再去括号.
解法1:原式
解法2:原式
典例解析
【例4】求比多项式5a2-2a-3ab+b2少5a2-ab的多项式.
【考点】整式的加减.
【分析】当整式是一个多项式,不是一个单项式时,应用括号把一个整式作为一个整体来加减.
解:依题意,列式为:
典例解析
【例5】化简求值:
(1)直接化简代入 已知x=1,y=-1,求5(2x2y)-2(4x-3x2y)的值.
(2)条件求值 (烟台)若3xm+5y2与x3yn的和是单项式,则mn_____.
(3)整体代入 已知x2-2y=1,那么2x2-4y+3=________.
【分析】先对多项式进行化简:根据整式的加减法则进行运算,再把未知数的值代入求解即可.
解:(1)5(2x2y-3x)-2(4x-3x2y)
=10x2y-15x-8x+6x2y =16x2y-23x
当x=1,y=-1时,原式 =16×12×(-1)-23×1
= -39
典例解析
【例5】化简求值:
(1)直接化简代入 已知x=1,y=-1,求5(2x2y)-2(4x-3x2y)的值.
(2)条件求值 (烟台)若3xm+5y2与x3yn的和是单项式,则mn_____.
(3)整体代入 已知x2-2y=1,那么2x2-4y+3=________.
【分析】根据和是单项式,从而可以得到两单项式必须为同类项,根据同类项的合并法则解题.
解:(2) 由题意知:3xm+5y2与x3yn是同类项
所以 m+5=3,n=2,解得,m=-2,n=2,
所以mn=(-2)2=4
典例解析
【例5】化简求值:
(1)直接化简代入 已知x=1,y=-1,求5(2x2y)-2(4x-3x2y)的值.
(2)条件求值 (烟台)若3xm+5y2与x3yn的和是单项式,则mn_____.
(3)整体代入 已知x2-2y=1,那么2x2-4y+3=________.
【分析】整体代入的一般做法是对代数式先进行化简,然后找到化简结果与已知条件之间的联系.
解:(3)因为2x2-4y+3=2(x2-2y)+3
而x2-2y=1
所以2x2-4y+3=2×1+3=5
典例解析
【例6】 已知多项式
是否存在m ,使此多项式与x无关?若不存在,说明理由;若存在,求出m 的值.
【分析】先对多项式进行化简,再进行判断,若要使原式与x无关,则需该项的系数为0,即有2m-6=0,所以m=3
解:原式
据题意得:2m-6=0,
即m=3
真题演练
一、选择题
1.(2015 崇左)下列各组中,不是同类项的是( )
A.52与25 B.﹣ab与ba
C.0.2a2b与﹣a2b D.a2b3与﹣a3b2
D
2.(2015 玉林)下列运算中,正确的是( )
A.3a+2b=5ab B.2a3+3a2=5a5
C.3a2b﹣3ba2=0 D.5a2﹣4a2=1
C
3.(2015 济宁)化简﹣16(x﹣0.5)的结果是( )
A.﹣16x﹣0.5 B.﹣16x+0.5
C.16x﹣8 D.﹣16x+8
D
真题演练
一、选择题
4.(2015 石城县模拟)如果单项式﹣xa+1y3与x2yb是同类项,那么a、b的值分别为( )
A.a=2,b=3 B.a=1,b=2
C.a=1,b=3 D.a=2,b=2
C
5.(2015秋 河南期中)若7x3y2和﹣11x3my2的和是单项式,则式子12m﹣24的值是( )
A.﹣3 B.﹣4 C.﹣5 D.﹣12
D
一、选择题
6.(2015 石峰区模拟)若﹣x3ym与xny是同类项,则m+n的值为( )
A.1 B.2 C.3 D.4
D
7.(2015 廊坊二模)如图1,将一个边长为a的正方形纸片剪去两个矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
A.2a﹣3b B.2a﹣4b C.4a﹣8b D.4a﹣10b
C
真题演练
3.(2015 湖州模拟)计算 2a﹣(﹣1+2a)= .
二、填空题
5
1
3
2.(2015 牡丹江)一列单项式:﹣x2,3x3,﹣5x4,7x5,…,按此规律排列,则第7个单项式为 .
﹣13x8
1.(2015 岳阳)单项式﹣ x2y3的次数是 .
4.(2015秋 开封校级月考)多项式﹣2m2+3m﹣ 的各项系数之积为 .
真题演练
7.(2015 临沂)观察下列关于x的单项式,探究其规律:
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是 .
6.(2015秋 海宁市校级期中)关于x,y的多项式4xy3﹣2ax2﹣3xy+x2﹣1不含x2的项,则a= .
二、填空题
5.(2015秋 无锡期中)已知多项式(4x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1),若多项式的值与字母x的取值无关,则ab= .
9
4029x2015
真题演练
三、解答题
1.(2015春 潜江校级期中)列式计算:
(1)﹣1减去 与 的和所得差是多少?
(2)一个多项式加上2x2﹣x+5等于4x2﹣6x﹣3,求这个多项式?
解:(2)根据题意得:
(4x2﹣6x﹣3)﹣(2x2﹣x+5)=4x2﹣6x﹣3﹣2x2+x﹣5
=2x2﹣5x﹣8.
解:(1)根据题意得:
真题演练
三、解答题
解:原式=4x﹣4﹣2x2﹣2﹣2x2+x
=﹣4x2+5x﹣6,
当x=2时,
原式=﹣16+10﹣6
=﹣12.
2.(2015春 绥阳县校级期末)化简并求值.
4(x﹣1)﹣2(x2+1)﹣(4x2﹣2x),其中x=2.
真题演练
三、解答题
3.(2015秋 东台市期中)多项式7xm+(k﹣1)x2﹣(2n+4)x﹣6是关于x的三次三项式,并且二次项系数为1,求m+n﹣k的值.
解:由7xm+(k﹣1)x2﹣(2n+4)x﹣6是关于x的三次三项式,二次项系数为1,得
解得
当
时,
m+n﹣k=3+(﹣2)﹣2=﹣1.
真题演练
三、解答题
4.(2015秋 和平区期中)已知关于x、y的
多项式5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1
(1)若该多项式不含三次项,求m的值;
(2)在(1)的条件下,当x2+y2=13,xy=﹣6时,求这个多项式的值.
解:(1)5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1
=5x2﹣2xy2﹣(3xy+4y2+9xy﹣2y2﹣2mxy2+7x2)﹣1
=5x2﹣2xy2﹣(12xy+2y2﹣2mxy2+7x2)﹣1
=5x2﹣2xy2﹣12xy﹣2y2+2mxy2﹣7x2﹣1
=﹣2x2﹣2y2﹣12xy+(﹣2+2m)xy2﹣1,
∵该多项式不含三次项,∴﹣2+2m=0,故m的值为:1
真题演练
三、解答题
4.(2015秋 和平区期中)已知关于x、y的
多项式5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1
(1)若该多项式不含三次项,求m的值;
(2)在(1)的条件下,当x2+y2=13,xy=﹣6时,求这个多项式的值.
解(2)∵原式=﹣2x2﹣2y2﹣12xy+(﹣2+2m)xy2﹣1
=﹣2(x2+y2)﹣12xy﹣1
=﹣2×13﹣12×(﹣6)﹣1
=45.
真题演练
三、解答题
5.(2015秋 商河县校级期中)(1)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简|a﹣c|+|b﹣c|+|a+b|.
(2)﹣2a2by+1与7b3a2是同类项,求代数式:3x2﹣6y2+3(xy﹣3y2)﹣(3x2+3xy+7y2)的值.
解(1)根据数轴上点的位置得:
a﹣c<0,b﹣c>0,a+b=0,
则原式=c﹣a+b﹣c+0
=b﹣a
真题演练
三、解答题
5.(2015秋 商河县校级期中)(1)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简|a﹣c|+|b﹣c|+|a+b|.
(2)﹣2a2by+1与7b3a2是同类项,求代数式:3x2﹣6y2+3(xy﹣3y2)﹣(3x2+3xy+7y2)的值.
解(2)∵﹣2a2by+1与7b3a2是同类项,
∴y+1=3,即y=2,
则原式=3x2﹣6y2+3xy﹣9y2﹣3x2﹣3xy﹣7y2
=﹣22y2=﹣88.
真题演练
再 见
下 课
第二章 《整式的加减》复习
人教版七年级数学上册
教学目标
1.教学目标
(1)梳理整式的相关概念,通过回顾单项式、多项式、整式及有关的概念,归纳概念之间的区别与联系;
(2)在正确合并同类项、准确运用去括号时的符号变化规律的基础上,达到可以熟练地进行整式的加减运算;
(3)通过分析实际问题中的数量关系,进一步体会用字母表示数的意义,通过对数与式运算的分析,体会“数式通性”,体会蕴含在具体问题中的数学思想和规律,以及数学知识之间“具体”与“抽象”的内在联系和数学的内在统一性.
目标解析
2.目标解析
达成目标(1)的标志:清晰地知道单项式、多项式、整式的概念,理解单项式的系数、次数,多项式的项、次数等,可以建立概念之间的联系;
达成目标(2)的标志:更加清晰地认识到进行整式的加减实际上就是将整式化简,化简的主要方法是合并多项式中的同类项和去括号,并体会整式的运算在解决有关计算问题中的作用;
目标(3)是“内容所蕴含的思想方法”,利用所熟悉的数的运算来学习式的运算,充分利用类比的思想方法,是贯穿于全章的重要的思想方法,感悟“数式通性”,并迁移到解决相关的问题之中,需要不断地在应用中提高认识水平.
复习导航
1.举出一些用单项式、多项式表示数量关系的实例.
2 .合并同类项和去括号是整式加减的基础,举例说明合并同类项和去括号的依据?
3.举例说明整式加减的运算法则.
知识梳理
知识结构图
一、整式的相关概念
1.单项式:
由数字或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
要点诠释:(1)单项式的系数是指单项式中的数字因数.
(2)单项式的次数是指单项式中所有字母的指数和.
2.多项式:
几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
要点诠释:(1)在多项式中,不含字母的项叫做常数项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
知识梳理
一、整式的相关概念
3. 多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
要点诠释:
(1)利用加法交换律重新排列时,各项应带着它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
4.整式:
单项式和多项式统称为整式.
知识梳理
二、整式的加减
1.同类项:
所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.
要点诠释:辨别同类项要把准“两相同,两无关”:
(1)“两相同”是指:①所含字母相同;②相同字母的指数相同;
(2)“两无关”是指:①与系数无关;②与字母的排列顺序无关.
2.合并同类项:
把多项式中的同类项合并成一项,叫做合并同类项.
要点诠释:合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.
知识梳理
一、整式的相关概念
3.去括号法则:
括号前面是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前面是“-”,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
4.添括号法则:
添括号后,括号前面是“+”,括号内各项的符号都不改变;添括号后,括号前面是“-”,括号内各项的符号都要改变.
知识梳理
5.整式的加减运算法则:
几个整式相加减,通常用括号把每一个整式括起来,再用加、减号连接,然后去括号,合并同类项.
典例解析
【例1】指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.
【考点】整式.
(1) a-3 (2) 5 (3) (4)
(5) 3xy (6) (7)
【分析】①分母中出现字母的式子不是整式,故 不是整式;
②π是常数而不是字母,故 是整式,也是单项式;
③(7)表示的是加、减关系而不是乘积关系,而单项式中不能有加减.
如 其实质为 .
典例解析
【例1】指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.
(1) a-3 (2) 5 (3) (4)
(5) 3xy (6) (7)
【解答】解:整式:(1)、(2)、(4)、(5)、(6)、(7)
单项式:(2)、(5)、(6),
其中:5的系数是5,次数是0;3xy的系数是3,次数是2; 的系数是 次数是1,多项式(1)、(4)、(7)且它们都是一次二项式.
典例解析
【例2】合并同类项.
【分析】同类项的定义中强调,除所含字母相同外,相同字母的指数也要相同.其中,常数项也是同类项.
合并同类项时,若不是同类项,则不需合并.
解:原式
解:原式
典例解析
【例3】计算:
【分析】根据多重括号的去括号法则,可由里向外,也可由外向里逐层推进,在计算过程中要注意符号的变化.若括号前是“-”号,在去括号时,括号里各项都应变号,若括号前有数字因数,应把数字因数乘到括号里,再去括号.
解法1:原式
解法2:原式
典例解析
【例4】求比多项式5a2-2a-3ab+b2少5a2-ab的多项式.
【考点】整式的加减.
【分析】当整式是一个多项式,不是一个单项式时,应用括号把一个整式作为一个整体来加减.
解:依题意,列式为:
典例解析
【例5】化简求值:
(1)直接化简代入 已知x=1,y=-1,求5(2x2y)-2(4x-3x2y)的值.
(2)条件求值 (烟台)若3xm+5y2与x3yn的和是单项式,则mn_____.
(3)整体代入 已知x2-2y=1,那么2x2-4y+3=________.
【分析】先对多项式进行化简:根据整式的加减法则进行运算,再把未知数的值代入求解即可.
解:(1)5(2x2y-3x)-2(4x-3x2y)
=10x2y-15x-8x+6x2y =16x2y-23x
当x=1,y=-1时,原式 =16×12×(-1)-23×1
= -39
典例解析
【例5】化简求值:
(1)直接化简代入 已知x=1,y=-1,求5(2x2y)-2(4x-3x2y)的值.
(2)条件求值 (烟台)若3xm+5y2与x3yn的和是单项式,则mn_____.
(3)整体代入 已知x2-2y=1,那么2x2-4y+3=________.
【分析】根据和是单项式,从而可以得到两单项式必须为同类项,根据同类项的合并法则解题.
解:(2) 由题意知:3xm+5y2与x3yn是同类项
所以 m+5=3,n=2,解得,m=-2,n=2,
所以mn=(-2)2=4
典例解析
【例5】化简求值:
(1)直接化简代入 已知x=1,y=-1,求5(2x2y)-2(4x-3x2y)的值.
(2)条件求值 (烟台)若3xm+5y2与x3yn的和是单项式,则mn_____.
(3)整体代入 已知x2-2y=1,那么2x2-4y+3=________.
【分析】整体代入的一般做法是对代数式先进行化简,然后找到化简结果与已知条件之间的联系.
解:(3)因为2x2-4y+3=2(x2-2y)+3
而x2-2y=1
所以2x2-4y+3=2×1+3=5
典例解析
【例6】 已知多项式
是否存在m ,使此多项式与x无关?若不存在,说明理由;若存在,求出m 的值.
【分析】先对多项式进行化简,再进行判断,若要使原式与x无关,则需该项的系数为0,即有2m-6=0,所以m=3
解:原式
据题意得:2m-6=0,
即m=3
真题演练
一、选择题
1.(2015 崇左)下列各组中,不是同类项的是( )
A.52与25 B.﹣ab与ba
C.0.2a2b与﹣a2b D.a2b3与﹣a3b2
D
2.(2015 玉林)下列运算中,正确的是( )
A.3a+2b=5ab B.2a3+3a2=5a5
C.3a2b﹣3ba2=0 D.5a2﹣4a2=1
C
3.(2015 济宁)化简﹣16(x﹣0.5)的结果是( )
A.﹣16x﹣0.5 B.﹣16x+0.5
C.16x﹣8 D.﹣16x+8
D
真题演练
一、选择题
4.(2015 石城县模拟)如果单项式﹣xa+1y3与x2yb是同类项,那么a、b的值分别为( )
A.a=2,b=3 B.a=1,b=2
C.a=1,b=3 D.a=2,b=2
C
5.(2015秋 河南期中)若7x3y2和﹣11x3my2的和是单项式,则式子12m﹣24的值是( )
A.﹣3 B.﹣4 C.﹣5 D.﹣12
D
一、选择题
6.(2015 石峰区模拟)若﹣x3ym与xny是同类项,则m+n的值为( )
A.1 B.2 C.3 D.4
D
7.(2015 廊坊二模)如图1,将一个边长为a的正方形纸片剪去两个矩形,得到一个“S”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
A.2a﹣3b B.2a﹣4b C.4a﹣8b D.4a﹣10b
C
真题演练
3.(2015 湖州模拟)计算 2a﹣(﹣1+2a)= .
二、填空题
5
1
3
2.(2015 牡丹江)一列单项式:﹣x2,3x3,﹣5x4,7x5,…,按此规律排列,则第7个单项式为 .
﹣13x8
1.(2015 岳阳)单项式﹣ x2y3的次数是 .
4.(2015秋 开封校级月考)多项式﹣2m2+3m﹣ 的各项系数之积为 .
真题演练
7.(2015 临沂)观察下列关于x的单项式,探究其规律:
x,3x2,5x3,7x4,9x5,11x6,…
按照上述规律,第2015个单项式是 .
6.(2015秋 海宁市校级期中)关于x,y的多项式4xy3﹣2ax2﹣3xy+x2﹣1不含x2的项,则a= .
二、填空题
5.(2015秋 无锡期中)已知多项式(4x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1),若多项式的值与字母x的取值无关,则ab= .
9
4029x2015
真题演练
三、解答题
1.(2015春 潜江校级期中)列式计算:
(1)﹣1减去 与 的和所得差是多少?
(2)一个多项式加上2x2﹣x+5等于4x2﹣6x﹣3,求这个多项式?
解:(2)根据题意得:
(4x2﹣6x﹣3)﹣(2x2﹣x+5)=4x2﹣6x﹣3﹣2x2+x﹣5
=2x2﹣5x﹣8.
解:(1)根据题意得:
真题演练
三、解答题
解:原式=4x﹣4﹣2x2﹣2﹣2x2+x
=﹣4x2+5x﹣6,
当x=2时,
原式=﹣16+10﹣6
=﹣12.
2.(2015春 绥阳县校级期末)化简并求值.
4(x﹣1)﹣2(x2+1)﹣(4x2﹣2x),其中x=2.
真题演练
三、解答题
3.(2015秋 东台市期中)多项式7xm+(k﹣1)x2﹣(2n+4)x﹣6是关于x的三次三项式,并且二次项系数为1,求m+n﹣k的值.
解:由7xm+(k﹣1)x2﹣(2n+4)x﹣6是关于x的三次三项式,二次项系数为1,得
解得
当
时,
m+n﹣k=3+(﹣2)﹣2=﹣1.
真题演练
三、解答题
4.(2015秋 和平区期中)已知关于x、y的
多项式5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1
(1)若该多项式不含三次项,求m的值;
(2)在(1)的条件下,当x2+y2=13,xy=﹣6时,求这个多项式的值.
解:(1)5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1
=5x2﹣2xy2﹣(3xy+4y2+9xy﹣2y2﹣2mxy2+7x2)﹣1
=5x2﹣2xy2﹣(12xy+2y2﹣2mxy2+7x2)﹣1
=5x2﹣2xy2﹣12xy﹣2y2+2mxy2﹣7x2﹣1
=﹣2x2﹣2y2﹣12xy+(﹣2+2m)xy2﹣1,
∵该多项式不含三次项,∴﹣2+2m=0,故m的值为:1
真题演练
三、解答题
4.(2015秋 和平区期中)已知关于x、y的
多项式5x2﹣2xy2﹣[3xy+4y2+(9xy﹣2y2﹣2mxy2)+7x2]﹣1
(1)若该多项式不含三次项,求m的值;
(2)在(1)的条件下,当x2+y2=13,xy=﹣6时,求这个多项式的值.
解(2)∵原式=﹣2x2﹣2y2﹣12xy+(﹣2+2m)xy2﹣1
=﹣2(x2+y2)﹣12xy﹣1
=﹣2×13﹣12×(﹣6)﹣1
=45.
真题演练
三、解答题
5.(2015秋 商河县校级期中)(1)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简|a﹣c|+|b﹣c|+|a+b|.
(2)﹣2a2by+1与7b3a2是同类项,求代数式:3x2﹣6y2+3(xy﹣3y2)﹣(3x2+3xy+7y2)的值.
解(1)根据数轴上点的位置得:
a﹣c<0,b﹣c>0,a+b=0,
则原式=c﹣a+b﹣c+0
=b﹣a
真题演练
三、解答题
5.(2015秋 商河县校级期中)(1)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简|a﹣c|+|b﹣c|+|a+b|.
(2)﹣2a2by+1与7b3a2是同类项,求代数式:3x2﹣6y2+3(xy﹣3y2)﹣(3x2+3xy+7y2)的值.
解(2)∵﹣2a2by+1与7b3a2是同类项,
∴y+1=3,即y=2,
则原式=3x2﹣6y2+3xy﹣9y2﹣3x2﹣3xy﹣7y2
=﹣22y2=﹣88.
真题演练
再 见
下 课
