河北省张家口市桥西区2023-2024学年七年级下学期期中数学试题(含答案)
文档属性
| 名称 | 河北省张家口市桥西区2023-2024学年七年级下学期期中数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 13:58:31 | ||
图片预览


文档简介
2023—2024学年度第二学期期中学情诊断测试
七年级 数学试卷
考生注意:
1.本试卷共4页,总分100分,考试时间90分钟;
2.请务必在答题纸上作答,写在试卷上的答案无效.考试结束,只收答题纸.
3.答卷前,请在答题纸上将姓名、班级、考场、座位号、准考证号填写清楚.
4.客观题答题,必须使用2B铅笔填涂,修改时用橡皮擦干净.
5.主观题答案须用黑色字迹钢笔、签字笔书写.
6.必须在答题纸上题号所对应的答题区域内作答,超出答题区域的书写,无效.
7.保持卷面清洁、完整.禁止对答题纸恶意折损,涂画,否则不能过扫描机器.
一、选择题(本大题共12个小题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算,则“?”为( )
A. B.2 C.3 D.9
2.如图,经过直线l外一点A画l的平行线,能画出( )
A.0条 B.1条 C.2条 D.无数条
3.若k为正整数,则表示的是( )
A.3个相乘 B.5个k相乘 C.2个相加 D.3个相加
4.研究表明,当每公顷氮肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量 0 34 67 101 135 202 259 336 404 471
土豆产量 15.2 21.4 25.7 32.3 34.1 39.5 43.2 43.5 40.8 30.8
根据表格中的数据,氮肥的施用量是( )kg时最适宜.
A.202 B.259 C.336 D.404
5.如图,用尺规作出,作图痕迹弧MN是( )
A.以点B为圆心,OD为半径的圆 B.以点B为圆心,DC为半径的圆
C.以点E为圆心,OD为半径的圆 D.以点E为圆心,DC为半径的圆
6.用简便方法计算时,变形正确的是( )
A. B.
C. D.
7.已知中,,,则的形状为( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
8.已知1纳米米,将纳米用科学记数法表示的结果是( )
A.米 B.米 C.米 D.米
9.如图,,对于结论Ⅰ和Ⅱ,下列判断正确的是结论Ⅰ:;结论Ⅱ:是的补角.( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
10.柿子熟了后会从树上落下来.下列图象可以大致刻画出柿子下落过程(即落地前)的速度变化情况的是( )
A. B.
C. D.
11.如图,,B、C、D在同一直线上,且,,则BD长( )
A.12 B.14 C.16 D.18
12.三边长度都是整数的三角形称为整数边三角形,若一个三角形的最长边长为8,则满足条件的整数边三角形共有( )
A.8个 B.10个 C.12个 D.20个
二、填空题(本大题共4个小题,每小题3分,共12分)
13.__________.
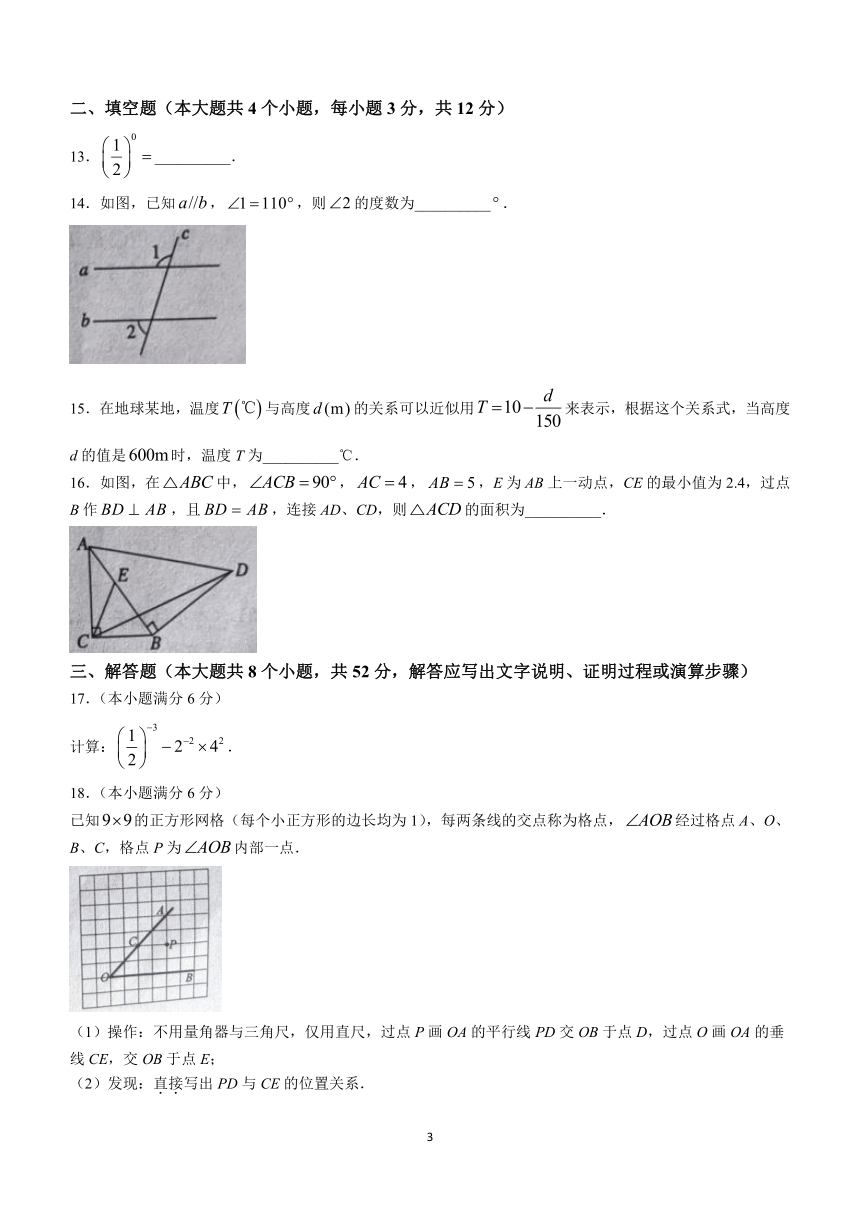
14.如图,已知,,则的度数为__________.
15.在地球某地,温度与高度的关系可以近似用来表示,根据这个关系式,当高度d的值是时,温度T为__________℃.
16.如图,在中,,,,E为AB上一动点,CE的最小值为2.4,过点B作,且,连接AD、CD,则的面积为__________.
三、解答题(本大题共8个小题,共52分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分6分)
计算:.
18.(本小题满分6分)
已知的正方形网格(每个小正方形的边长均为1),每两条线的交点称为格点,经过格点A、O、B、C,格点P为内部一点.
(1)操作:不用量角器与三角尺,仅用直尺,过点P画OA的平行线PD交OB于点D,过点O画OA的垂线CE,交OB于点E;
(2)发现:直接写出PD与CE的位置关系.
19.(本小题满分6分)
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
(1)求手掌捂住的多项式;
(2)若,,求所捂多项式的值.
20.(本小题满分6分)
共享单车为市民的绿色出行提供了方便.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,,,已知AM与CB平行,求的度数.
21.(本小题满分6分)
嘉嘉计算一道整式乘法的题:,由于嘉嘉在解题过程中,抄错了第一个多项式中a前面的符号,把“-”写成了“+”,得到的结果为.
(1)求a的值;
(2)计算这道整式乘法的正确结果.
22.(本小题满分6分)
如图①是琪琪制作的燕子风筝,燕子风筝的骨架图如图②所示,,,,,求的大小.
23.(本小题满分7分)
如图①,正方形ABCD的边长为,F为AB边上一点,动点P以的速度沿的路径向终点A运动.设运动时间为,的面积为,S与t的关系图象如图②所示.
(1)求线段BF的长及a的值;
(2)的面积S为时,直接写出t的值.
24.(本小题满分9分)
定义:从的顶点出发,在角的内部作一条射线,若该射线将分得的两个角中有一个角与互为补角,则称该射线为的“好线”.
如图,点O在直线AB上,OC、OD在直线AB上方,且,射线OE是的“好线”.
(1)若,且OE在内部,求的度数;
(2)若OE恰好平分,求的度数;
(3)若OF是的平分线,OG是的平分线,直接写出与的数量关系.
2023—2024学年度第二学期七年级期中学情诊断测试
数学参考答案及评分参考
一、选择题(每小题3分,共36分)
题号 1 2 3 4 5 6
答案 D B A C D B
题号 7 8 9 10 11 12
答案 A C A C B D
二、填空题(每空3分.共12分.)
13.1 14.70 15.6 16.14
三、解答题(本大题8个小题,共52分)
17.解:原式.
18.解:(1)如图所示:
(2)互相垂直()
19.解:
(1)设多项式为A,则.
(2),,原式.
20.解:
,CD都与地面平行,,,
,,
与CB平行,.
21.解:(1)根据题意可得,,
,解得;
(2).
22.解:,,即,
在与中,,,.
23.解:(1)当点P运动到点C时,结合图②可得:,
即:,,
由图②可得:点P运动后,,即:,
,解得:;
(2)或时,的面积S为.
①当点P在BC段时:
,,解得:;
②当点P在DA段时:,,解得:,
综上所述:或时,的面积S为10.
24.解:
(1)如图①,由于射线OE是的“好线”,
当时,,,
,,,
如图②,由于射线OE是的“好线”,
当时,,,
,因此或.
(2)若OE恰好平分,,;
(3)或.
七年级 数学试卷
考生注意:
1.本试卷共4页,总分100分,考试时间90分钟;
2.请务必在答题纸上作答,写在试卷上的答案无效.考试结束,只收答题纸.
3.答卷前,请在答题纸上将姓名、班级、考场、座位号、准考证号填写清楚.
4.客观题答题,必须使用2B铅笔填涂,修改时用橡皮擦干净.
5.主观题答案须用黑色字迹钢笔、签字笔书写.
6.必须在答题纸上题号所对应的答题区域内作答,超出答题区域的书写,无效.
7.保持卷面清洁、完整.禁止对答题纸恶意折损,涂画,否则不能过扫描机器.
一、选择题(本大题共12个小题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算,则“?”为( )
A. B.2 C.3 D.9
2.如图,经过直线l外一点A画l的平行线,能画出( )
A.0条 B.1条 C.2条 D.无数条
3.若k为正整数,则表示的是( )
A.3个相乘 B.5个k相乘 C.2个相加 D.3个相加
4.研究表明,当每公顷氮肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量 0 34 67 101 135 202 259 336 404 471
土豆产量 15.2 21.4 25.7 32.3 34.1 39.5 43.2 43.5 40.8 30.8
根据表格中的数据,氮肥的施用量是( )kg时最适宜.
A.202 B.259 C.336 D.404
5.如图,用尺规作出,作图痕迹弧MN是( )
A.以点B为圆心,OD为半径的圆 B.以点B为圆心,DC为半径的圆
C.以点E为圆心,OD为半径的圆 D.以点E为圆心,DC为半径的圆
6.用简便方法计算时,变形正确的是( )
A. B.
C. D.
7.已知中,,,则的形状为( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
8.已知1纳米米,将纳米用科学记数法表示的结果是( )
A.米 B.米 C.米 D.米
9.如图,,对于结论Ⅰ和Ⅱ,下列判断正确的是结论Ⅰ:;结论Ⅱ:是的补角.( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
10.柿子熟了后会从树上落下来.下列图象可以大致刻画出柿子下落过程(即落地前)的速度变化情况的是( )
A. B.
C. D.
11.如图,,B、C、D在同一直线上,且,,则BD长( )
A.12 B.14 C.16 D.18
12.三边长度都是整数的三角形称为整数边三角形,若一个三角形的最长边长为8,则满足条件的整数边三角形共有( )
A.8个 B.10个 C.12个 D.20个
二、填空题(本大题共4个小题,每小题3分,共12分)
13.__________.
14.如图,已知,,则的度数为__________.
15.在地球某地,温度与高度的关系可以近似用来表示,根据这个关系式,当高度d的值是时,温度T为__________℃.
16.如图,在中,,,,E为AB上一动点,CE的最小值为2.4,过点B作,且,连接AD、CD,则的面积为__________.
三、解答题(本大题共8个小题,共52分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分6分)
计算:.
18.(本小题满分6分)
已知的正方形网格(每个小正方形的边长均为1),每两条线的交点称为格点,经过格点A、O、B、C,格点P为内部一点.
(1)操作:不用量角器与三角尺,仅用直尺,过点P画OA的平行线PD交OB于点D,过点O画OA的垂线CE,交OB于点E;
(2)发现:直接写出PD与CE的位置关系.
19.(本小题满分6分)
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
(1)求手掌捂住的多项式;
(2)若,,求所捂多项式的值.
20.(本小题满分6分)
共享单车为市民的绿色出行提供了方便.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,,,已知AM与CB平行,求的度数.
21.(本小题满分6分)
嘉嘉计算一道整式乘法的题:,由于嘉嘉在解题过程中,抄错了第一个多项式中a前面的符号,把“-”写成了“+”,得到的结果为.
(1)求a的值;
(2)计算这道整式乘法的正确结果.
22.(本小题满分6分)
如图①是琪琪制作的燕子风筝,燕子风筝的骨架图如图②所示,,,,,求的大小.
23.(本小题满分7分)
如图①,正方形ABCD的边长为,F为AB边上一点,动点P以的速度沿的路径向终点A运动.设运动时间为,的面积为,S与t的关系图象如图②所示.
(1)求线段BF的长及a的值;
(2)的面积S为时,直接写出t的值.
24.(本小题满分9分)
定义:从的顶点出发,在角的内部作一条射线,若该射线将分得的两个角中有一个角与互为补角,则称该射线为的“好线”.
如图,点O在直线AB上,OC、OD在直线AB上方,且,射线OE是的“好线”.
(1)若,且OE在内部,求的度数;
(2)若OE恰好平分,求的度数;
(3)若OF是的平分线,OG是的平分线,直接写出与的数量关系.
2023—2024学年度第二学期七年级期中学情诊断测试
数学参考答案及评分参考
一、选择题(每小题3分,共36分)
题号 1 2 3 4 5 6
答案 D B A C D B
题号 7 8 9 10 11 12
答案 A C A C B D
二、填空题(每空3分.共12分.)
13.1 14.70 15.6 16.14
三、解答题(本大题8个小题,共52分)
17.解:原式.
18.解:(1)如图所示:
(2)互相垂直()
19.解:
(1)设多项式为A,则.
(2),,原式.
20.解:
,CD都与地面平行,,,
,,
与CB平行,.
21.解:(1)根据题意可得,,
,解得;
(2).
22.解:,,即,
在与中,,,.
23.解:(1)当点P运动到点C时,结合图②可得:,
即:,,
由图②可得:点P运动后,,即:,
,解得:;
(2)或时,的面积S为.
①当点P在BC段时:
,,解得:;
②当点P在DA段时:,,解得:,
综上所述:或时,的面积S为10.
24.解:
(1)如图①,由于射线OE是的“好线”,
当时,,,
,,,
如图②,由于射线OE是的“好线”,
当时,,,
,因此或.
(2)若OE恰好平分,,;
(3)或.
同课章节目录
