2.4.2 平面向量及运算的坐标表示 课件(共23张PPT)-2023-2024学年高一下学期数学北师版(2019)必修第二册
文档属性
| 名称 | 2.4.2 平面向量及运算的坐标表示 课件(共23张PPT)-2023-2024学年高一下学期数学北师版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 766.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第二章 平面向量及其应用
2.4.2 平面向量及
运算的坐标表示
课程导入入
新知探究
应用举例
课堂练习
课堂小结
布置作业
1.借助平面直角坐标系,掌握平面向量的正交分解及其坐标表示;
2.掌握两个向量和、差及数乘向量的坐标运算法则;
3.能用坐标表示平面向量共线的条件.
平面向量的坐标表示和运算.
平面向量线性运算和坐标表示下的共线关系表达.
课程导入入
新知探究
应用举例
课堂练习
课堂小结
布置作业
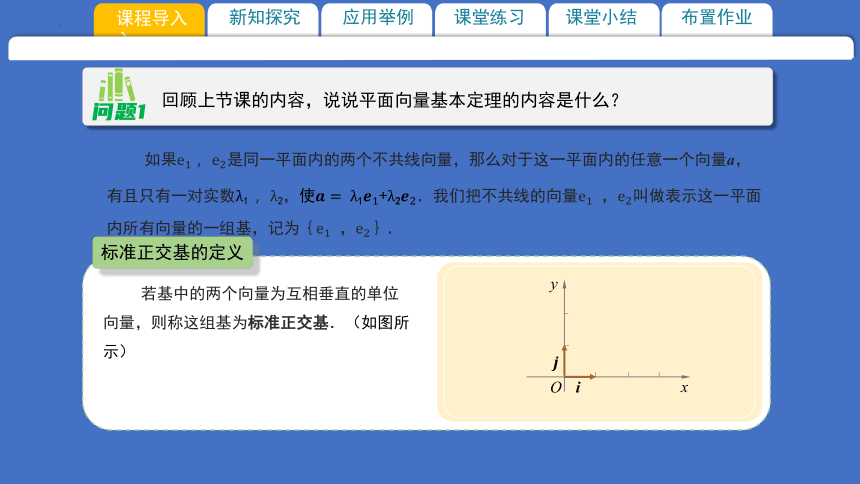
回顾上节课的内容,说说平面向量基本定理的内容是什么?
如果是同一平面内的两个不共线向量,那么对于这一平面内的任意一个向量a,有且只有一对实数1 2,使1+2.我们把不共线的向量 ,叫做表示这一平面内所有向量的一组基,记为{ ,}.
若基中的两个向量为互相垂直的单位向量,则称这组基为标准正交基.(如图所示)
标准正交基的定义
i
O
x
y
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
i
O
x
y
a
P(x,y)
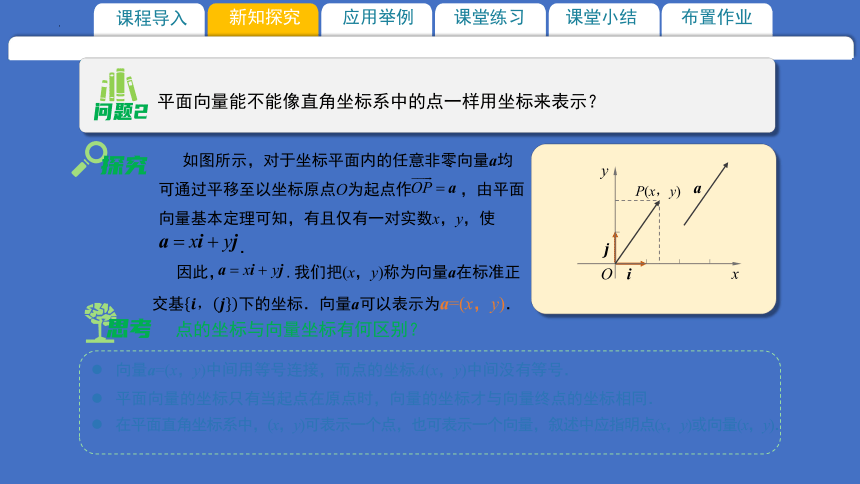
因此, . 我们把(x,y)称为向量a在标准正交基下的坐标.向量a可以表示为a=(x,y).
如图所示,对于坐标平面内的任意非零向量a均可通过平移至以坐标原点O为起点作 ,由平面向量基本定理可知,有且仅有一对实数x,y,使
.
点的坐标与向量坐标有何区别?
向量a=(x,y)中间用等号连接,而点的坐标A(x,y)中间没有等号.
平面向量的坐标只有当起点在原点时,向量的坐标才与向量终点的坐标相同.
在平面直角坐标系中,(x,y)可表示一个点,也可表示一个向量,叙述中应指明点(x,y)或向量(x,y).
平面向量能不能像直角坐标系中的点一样用坐标来表示?
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
平面向量可以用坐标表示,平面向量的运算可以用坐标来表示吗?
向量的加减法可否用坐标进行运算?
分步
第1步,设a=(x1,y1),b=(x2,y2),
则a=x1i+y1j,b= x2i+y2j.
第2步,根据向量的运算律,
可得 a+b=(x1i+ y1j)+(x2i+ y2j)=(x1+ x2)i+(y1+ y2)j,
向量的数乘运算,可以用坐标表示吗?
a+b=(x1+x2,y1+y2)
a-b=(x1-x2,y1-y2)
即 a+b=(x1+x2,y1+y2).
同理 a-b=(x1-x2,y1-y2).
设
即 ,) .
,)
向量和差坐标运算
数乘向量坐标运算
给出平面向量的起点和终点坐标,怎样求向量的坐标?
如图所示,设点A (x1,y1),B(x2,y2),
.
即
,
确定向量的坐标表示
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
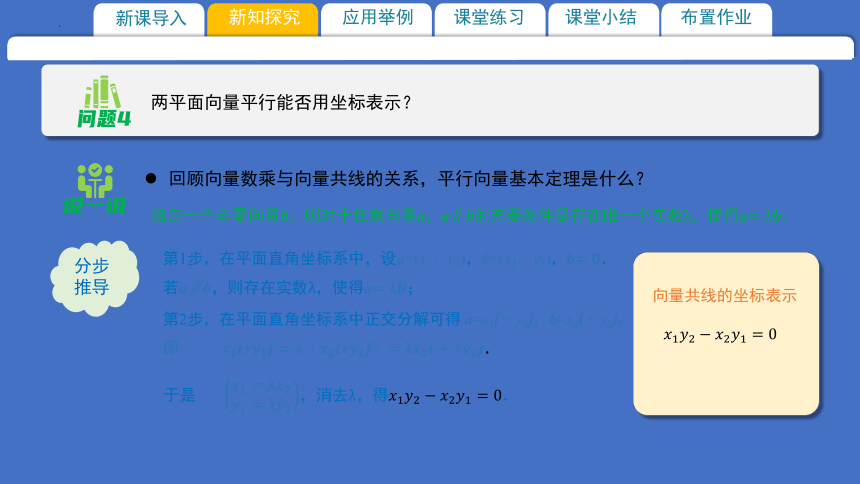
两平面向量平行能否用坐标表示?
第1步,在平面直角坐标系中,设a=(x1,y1),b=(x2,y2),b.
若a∥b,则存在实数,使得a;
第2步,在平面直角坐标系中正交分解可得 a=x1i + y1j,b=x2i + y2j,即+(+).
回顾向量数乘与向量共线的关系,平行向量基本定理是什么?
给定一个非零向量b,则对于任意向量a,a∥b的充要条件是存在唯一个实数,使得a.
分步推导
向量共线的坐标表示
于是 ,消去,得.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
前面的三个问题推导出了什么结果?
(2)向量能不能像平面坐标系中点一样给出坐标表示?
利用平面直角坐标系,通过建立标准正交基,可以实现平面向量的坐标表示.
平面内两个向量和、差、数乘及共线都拥有自己的坐标运算法则.
(3)平面向量可以用坐标表示,向量的运算可以用坐标来运算吗?
(4)平面向量平行能否用坐标表示?
通过这三个问题的探究,可以发现平面内任意向量都能与有序实数对一一对应,同时向量的坐标运算符合实数的运算规律,我们可以利用它求点的坐标,判断向量共线等问题,从而实现形与数的统一.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
和差
两个向量和与差的坐标分别等于这两个向量对应坐标的和与差.
坐标
一个向量的坐标等于其终点的坐标减去起点的坐标.
平行
向量ab(b)共线的充要条件是.
数乘
实数与向量数乘的坐标等于这个实数与向量的相应坐标的乘积.
平面向量坐标表示和坐标运算的概括
(1)向量 与向量 的坐标相同.
(2)两个向量的终点不同,则这两个向量
的坐标一定不同.
(3)两向量差的坐标与两向量的顺序无关.
(4)向量(2,4)与向量(-4,-6)反向.
(5)若a∥b,a=(x1,y1),b=(x2,y2),
则必有 .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
判断正误并说明理由:
平面向量的坐标表示、和差数乘运算法则.
平面向量共线的条件及应用.
判断依据
根据两向量差的运算,两向量差的坐标与两向量的顺序有关.
对于同一个向量,无论位置在哪里,坐标都一样.
因为(-4,-6)=-2(2,4),所以两个
向量相反.
若向量b为零向量,则不成立.
向量的坐标为点B的坐标减去点A的坐标,向量的坐标为点A的坐标减去点B的坐标.
你能用向量的坐标运算来推导出给定线段的中点坐标吗
建立直角坐标系,利用坐标运算进行推导.
分步
第1步,设A (x1,y1),B(x2,y2),M是线段AB的中点;
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
第2步, , ,由向量的线性运算可知 ;
第3步,所以中点M的坐标是 .
若点A (x1,y1),B(x2,y2), M是线段AB的中点坐标(x,y),则
中点坐标公式
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内作直线运动,先画出下列位移向量在基下的正交分解,再求出下列位移向量的坐标:
(1)向量a表示沿东北方向移动了2个单位长度;
(2)向量b表示沿北偏西30°方向移动了3个单位长度;
(3)向量c表示沿南偏东60°方向移动了4个单位长度.
解:第1步,建立直角坐标系,设a=(x1,y1),b=(x2,y2),c=(x3,y3) ,作出以上向量在基下的正交分解;
第2步, , ;
,
,
;
.
第3步,因此
,
,
.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
运用平面向量和、差、数乘的坐标运算法则直接计算
已知a=(2,1),b=(-3,4),求a+b,a-b,3a+4b的坐标.
解:a+b=(2,1)+ (-3,4)= (-1,5),
a-b=(2,1) - (-3,4)= (5,-3),
3a+4b=3(2,1)+4(-3,4)= (6,3)+ (-12,16)= (-6,19).
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
已知点A(1,0),B(0,2),C(-1,-2),用向量的方法求 的顶点D的坐标.
解:第1步,设点D的坐标为(x,y) ,建立直角坐标系;
第3步,所以点D的坐标为(0,-4).
第2步,由 ,得
(0,2)-(1,0)=(-1,-2)-(x,y),
即(-1,2)=(-1-x,-2-y),
所以, 解得
第2步,设点M的坐标为(x,y),则 =(x-3,y-4).
因此, 解得
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
所以点M的坐标为(,).
已知点A(2,-4),B(-1,3),C(3,4),且 ,求点M的坐标.
根据一个向量的坐标等于其终点的坐标减去起点的坐标,用坐标表示出已知向量,设未知点,再运用平面向量的坐标表示、和差数乘运算法则计算出未知量.
解:第1步,根据题意,得 = (2-3,-4-4) = (-1,-8), = (-1-3,3-4) = (-4,-1).
于是 =2 (-1,-8) + 3(-4,-1) = (-2,-16) + (-12,-3) = (-14,-19);
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
所以当k=-2或k=11时,A,B,C三点共线.
第2步,根据向量平行的坐标表示,得(4-k) ( k-5)-6-7)=0.
解得k=-2或k=11.
已知O是坐标原点, = (k,12), = (4,5), = (10,k).当k为何值时,
A,B,C三点共线?
要使A,B,C三点共线,只需 , 共线,运用坐标表示的平面向量共线公式即可.
解:第1步,根据题意, =(4,5) - (k,12)= (4-k,-7).
=(10,k) - (4,5) = (6,k-5).
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
解:由平面向量平行的坐标公式可得2=-6 .
A
故选B.
B
已知向量a=(2,6),b=(-1,),若a∥b,则= ( ).
A. 3 B. -3
C. D.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
解:设点D(m,n).由题意得(4,3)=2(m,n-2)= (2m,2n-4),
A
故选A.
A
已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且 , 则顶点D的坐标为 ( ).
A. B.
C. D.
故 ,解得 ,即点D(2, ) .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
A
故选A.
A
已知O(0,0),A(-1,3),B(2,-4), ,若点P在y轴上,则实数m的值为( ).
A. B.
C. D.
解:由题意可得 , ,所以 ,
又点P在y轴上,所以 ,得 .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
故选C.
C
如图所示,已知线段OA的长度为2,与x轴正半轴所成夹角为30°,OB的长度为2,
与x轴负半轴所成夹角为60°,C是AB的中点,则 的坐标是( ).
B.
C. D.
解:由题意知, , ,故A的坐标为 ( ,1);
同理 , ,
故B的坐标为 ( , ),
根据中点坐标公式可得C的坐标为 .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
1.向量的坐标表示是向量的另一种表示形式,也可以称之为向量的代数表示,其背景是平面向量基本定理;
2.向量的坐标表示为我们进行向量的运算提供了方便;
3.向量的坐标表示使得我们借助数的运算对图形的几何性质展开研究,体现了数形结合思想方法的应用.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
坐标表示
一个向量的坐标等于其终点的坐标减去起点的坐标.
运算法则
平面向量及运算的坐标表示
向量和差:两个向量和与差的坐标分别等于这两个向量对应坐标的和与差.
任意非零向量都能在平面直角坐标系中做标准正交基下的分解,从而得到向量的坐标表示.
结构框图
数乘:实数与向量数乘的坐标等于这个实数与向量的相应坐标的乘积.
共线:向量ab(b)共线的充要条件是
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
教材第99页练习第2,3 ,5题.
再 见
第二章 平面向量及其应用
2.4.2 平面向量及
运算的坐标表示
课程导入入
新知探究
应用举例
课堂练习
课堂小结
布置作业
1.借助平面直角坐标系,掌握平面向量的正交分解及其坐标表示;
2.掌握两个向量和、差及数乘向量的坐标运算法则;
3.能用坐标表示平面向量共线的条件.
平面向量的坐标表示和运算.
平面向量线性运算和坐标表示下的共线关系表达.
课程导入入
新知探究
应用举例
课堂练习
课堂小结
布置作业
回顾上节课的内容,说说平面向量基本定理的内容是什么?
如果是同一平面内的两个不共线向量,那么对于这一平面内的任意一个向量a,有且只有一对实数1 2,使1+2.我们把不共线的向量 ,叫做表示这一平面内所有向量的一组基,记为{ ,}.
若基中的两个向量为互相垂直的单位向量,则称这组基为标准正交基.(如图所示)
标准正交基的定义
i
O
x
y
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
i
O
x
y
a
P(x,y)
因此, . 我们把(x,y)称为向量a在标准正交基下的坐标.向量a可以表示为a=(x,y).
如图所示,对于坐标平面内的任意非零向量a均可通过平移至以坐标原点O为起点作 ,由平面向量基本定理可知,有且仅有一对实数x,y,使
.
点的坐标与向量坐标有何区别?
向量a=(x,y)中间用等号连接,而点的坐标A(x,y)中间没有等号.
平面向量的坐标只有当起点在原点时,向量的坐标才与向量终点的坐标相同.
在平面直角坐标系中,(x,y)可表示一个点,也可表示一个向量,叙述中应指明点(x,y)或向量(x,y).
平面向量能不能像直角坐标系中的点一样用坐标来表示?
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
平面向量可以用坐标表示,平面向量的运算可以用坐标来表示吗?
向量的加减法可否用坐标进行运算?
分步
第1步,设a=(x1,y1),b=(x2,y2),
则a=x1i+y1j,b= x2i+y2j.
第2步,根据向量的运算律,
可得 a+b=(x1i+ y1j)+(x2i+ y2j)=(x1+ x2)i+(y1+ y2)j,
向量的数乘运算,可以用坐标表示吗?
a+b=(x1+x2,y1+y2)
a-b=(x1-x2,y1-y2)
即 a+b=(x1+x2,y1+y2).
同理 a-b=(x1-x2,y1-y2).
设
即 ,) .
,)
向量和差坐标运算
数乘向量坐标运算
给出平面向量的起点和终点坐标,怎样求向量的坐标?
如图所示,设点A (x1,y1),B(x2,y2),
.
即
,
确定向量的坐标表示
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
两平面向量平行能否用坐标表示?
第1步,在平面直角坐标系中,设a=(x1,y1),b=(x2,y2),b.
若a∥b,则存在实数,使得a;
第2步,在平面直角坐标系中正交分解可得 a=x1i + y1j,b=x2i + y2j,即+(+).
回顾向量数乘与向量共线的关系,平行向量基本定理是什么?
给定一个非零向量b,则对于任意向量a,a∥b的充要条件是存在唯一个实数,使得a.
分步推导
向量共线的坐标表示
于是 ,消去,得.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
前面的三个问题推导出了什么结果?
(2)向量能不能像平面坐标系中点一样给出坐标表示?
利用平面直角坐标系,通过建立标准正交基,可以实现平面向量的坐标表示.
平面内两个向量和、差、数乘及共线都拥有自己的坐标运算法则.
(3)平面向量可以用坐标表示,向量的运算可以用坐标来运算吗?
(4)平面向量平行能否用坐标表示?
通过这三个问题的探究,可以发现平面内任意向量都能与有序实数对一一对应,同时向量的坐标运算符合实数的运算规律,我们可以利用它求点的坐标,判断向量共线等问题,从而实现形与数的统一.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
和差
两个向量和与差的坐标分别等于这两个向量对应坐标的和与差.
坐标
一个向量的坐标等于其终点的坐标减去起点的坐标.
平行
向量ab(b)共线的充要条件是.
数乘
实数与向量数乘的坐标等于这个实数与向量的相应坐标的乘积.
平面向量坐标表示和坐标运算的概括
(1)向量 与向量 的坐标相同.
(2)两个向量的终点不同,则这两个向量
的坐标一定不同.
(3)两向量差的坐标与两向量的顺序无关.
(4)向量(2,4)与向量(-4,-6)反向.
(5)若a∥b,a=(x1,y1),b=(x2,y2),
则必有 .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
判断正误并说明理由:
平面向量的坐标表示、和差数乘运算法则.
平面向量共线的条件及应用.
判断依据
根据两向量差的运算,两向量差的坐标与两向量的顺序有关.
对于同一个向量,无论位置在哪里,坐标都一样.
因为(-4,-6)=-2(2,4),所以两个
向量相反.
若向量b为零向量,则不成立.
向量的坐标为点B的坐标减去点A的坐标,向量的坐标为点A的坐标减去点B的坐标.
你能用向量的坐标运算来推导出给定线段的中点坐标吗
建立直角坐标系,利用坐标运算进行推导.
分步
第1步,设A (x1,y1),B(x2,y2),M是线段AB的中点;
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
第2步, , ,由向量的线性运算可知 ;
第3步,所以中点M的坐标是 .
若点A (x1,y1),B(x2,y2), M是线段AB的中点坐标(x,y),则
中点坐标公式
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内作直线运动,先画出下列位移向量在基下的正交分解,再求出下列位移向量的坐标:
(1)向量a表示沿东北方向移动了2个单位长度;
(2)向量b表示沿北偏西30°方向移动了3个单位长度;
(3)向量c表示沿南偏东60°方向移动了4个单位长度.
解:第1步,建立直角坐标系,设a=(x1,y1),b=(x2,y2),c=(x3,y3) ,作出以上向量在基下的正交分解;
第2步, , ;
,
,
;
.
第3步,因此
,
,
.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
运用平面向量和、差、数乘的坐标运算法则直接计算
已知a=(2,1),b=(-3,4),求a+b,a-b,3a+4b的坐标.
解:a+b=(2,1)+ (-3,4)= (-1,5),
a-b=(2,1) - (-3,4)= (5,-3),
3a+4b=3(2,1)+4(-3,4)= (6,3)+ (-12,16)= (-6,19).
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
已知点A(1,0),B(0,2),C(-1,-2),用向量的方法求 的顶点D的坐标.
解:第1步,设点D的坐标为(x,y) ,建立直角坐标系;
第3步,所以点D的坐标为(0,-4).
第2步,由 ,得
(0,2)-(1,0)=(-1,-2)-(x,y),
即(-1,2)=(-1-x,-2-y),
所以, 解得
第2步,设点M的坐标为(x,y),则 =(x-3,y-4).
因此, 解得
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
所以点M的坐标为(,).
已知点A(2,-4),B(-1,3),C(3,4),且 ,求点M的坐标.
根据一个向量的坐标等于其终点的坐标减去起点的坐标,用坐标表示出已知向量,设未知点,再运用平面向量的坐标表示、和差数乘运算法则计算出未知量.
解:第1步,根据题意,得 = (2-3,-4-4) = (-1,-8), = (-1-3,3-4) = (-4,-1).
于是 =2 (-1,-8) + 3(-4,-1) = (-2,-16) + (-12,-3) = (-14,-19);
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
所以当k=-2或k=11时,A,B,C三点共线.
第2步,根据向量平行的坐标表示,得(4-k) ( k-5)-6-7)=0.
解得k=-2或k=11.
已知O是坐标原点, = (k,12), = (4,5), = (10,k).当k为何值时,
A,B,C三点共线?
要使A,B,C三点共线,只需 , 共线,运用坐标表示的平面向量共线公式即可.
解:第1步,根据题意, =(4,5) - (k,12)= (4-k,-7).
=(10,k) - (4,5) = (6,k-5).
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
解:由平面向量平行的坐标公式可得2=-6 .
A
故选B.
B
已知向量a=(2,6),b=(-1,),若a∥b,则= ( ).
A. 3 B. -3
C. D.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
解:设点D(m,n).由题意得(4,3)=2(m,n-2)= (2m,2n-4),
A
故选A.
A
已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且 , 则顶点D的坐标为 ( ).
A. B.
C. D.
故 ,解得 ,即点D(2, ) .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
A
故选A.
A
已知O(0,0),A(-1,3),B(2,-4), ,若点P在y轴上,则实数m的值为( ).
A. B.
C. D.
解:由题意可得 , ,所以 ,
又点P在y轴上,所以 ,得 .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
故选C.
C
如图所示,已知线段OA的长度为2,与x轴正半轴所成夹角为30°,OB的长度为2,
与x轴负半轴所成夹角为60°,C是AB的中点,则 的坐标是( ).
B.
C. D.
解:由题意知, , ,故A的坐标为 ( ,1);
同理 , ,
故B的坐标为 ( , ),
根据中点坐标公式可得C的坐标为 .
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
1.向量的坐标表示是向量的另一种表示形式,也可以称之为向量的代数表示,其背景是平面向量基本定理;
2.向量的坐标表示为我们进行向量的运算提供了方便;
3.向量的坐标表示使得我们借助数的运算对图形的几何性质展开研究,体现了数形结合思想方法的应用.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
坐标表示
一个向量的坐标等于其终点的坐标减去起点的坐标.
运算法则
平面向量及运算的坐标表示
向量和差:两个向量和与差的坐标分别等于这两个向量对应坐标的和与差.
任意非零向量都能在平面直角坐标系中做标准正交基下的分解,从而得到向量的坐标表示.
结构框图
数乘:实数与向量数乘的坐标等于这个实数与向量的相应坐标的乘积.
共线:向量ab(b)共线的充要条件是
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
教材第99页练习第2,3 ,5题.
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
