陕西省西安市工业大学附属中学2023-2024学年高二下学期期中考试数学试题(含解析)
文档属性
| 名称 | 陕西省西安市工业大学附属中学2023-2024学年高二下学期期中考试数学试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 459.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览




文档简介
陕西省西安市工业大学附属中2023-2024学年高二下学期期中考试
数学试题
一、单选题:(本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的。
1.(5分)计算的值是( )
A.72 B.102 C.507 D.510
2.(5分)已知等比数列{an}的公比为正数,且a3 a9=4a52,a2=1,则a1=( )
A.4 B.2 C.1 D.
3.(5分)某校迎新晚会上有A,B,C,D,E,F共6个节目,为了考虑整体效果,对节目演出顺序有如下要求:节目A,B不相邻,节目D,F必须连在一起,则不同的节目编排方案种数为( )
A.60 B.72 C.120 D.144
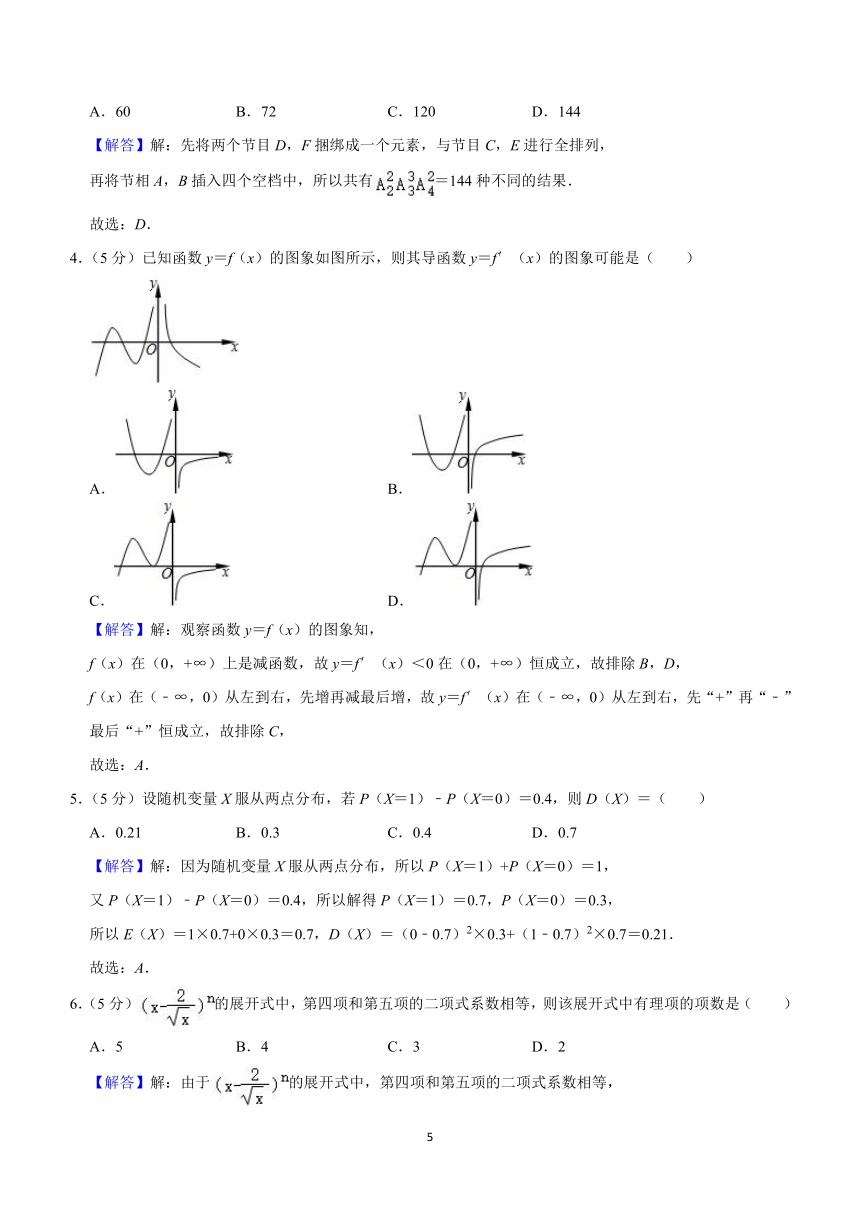
4.(5分)已知函数y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )
A. B.
C. D.
5.(5分)设随机变量X服从两点分布,若P(X=1)﹣P(X=0)=0.4,则D(X)=( )
A.0.21 B.0.3 C.0.4 D.0.7
6.(5分)的展开式中,第四项和第五项的二项式系数相等,则该展开式中有理项的项数是( )
A.5 B.4 C.3 D.2
7.(5分)将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( )
A.420 B.180 C.64 D.25
8.(5分)已知实数a,b,c成公差非零的等差数列,集合A={(x,y)|ax+by+c=0},P(﹣3,2),N(2,3),M∈A,若∥(a,b),则|MN|的最大值是( )
A.4 B.5 C. D.
二、多选题:(本大题共3小题,每个小题6分,共18分.全部选对得6分,部分选对得3分,有选错的得0分.)
(多选)9.(6分)若P(A)=,P(B)=,P(B|A)=,则下列说法正确的是( )
A. B.事件A与B相互独立
C. D.
(多选)10.(6分)在平面直角坐标系xOy中,过抛物线C:y2=4x的焦点F作直线l交抛物线C于A,B两点,则( )
A.|AB|的最小值为2
B.以线段AF为直径的圆与y轴相切
C.
D.
(多选)11.(6分)若,则下列等式正确的有( )
A.a0=1
B.a3=160
C.a0+a2+a4+a6=365
D.a1+2a2+3a3+ +6a6=12
三、填空题:(本大题共3小题,每小题5分,共15分把答案填在答题卡中的横线上.)
12.(5分)的展开式中x2y6的系数为 (用数字作答).
13.(5分)设F1,F2为椭圆的两个焦点,点P在椭圆C上,若,则|PF1| |PF2|= .
14.(5分)设函数(a,b∈R)在区间[1,3]上总存在零点,则a2+b2的最小值为 .
四、解答题:(本大题共5小题,共77分。解答应写出必要的文字说明、证明过程或演算步骤。)
15.(13分)中国传统文化中,过春节吃饺子,饺子是我国的传统美食,不仅味道鲜美而且寓意美好.现有甲、乙两个箱子装有大小、外观均相同的速冻饺子,已知甲箱中有3盒肉馅的“饺子”,2盒三鲜馅的“饺子”和5盒青菜馅的“饺子”,乙箱中有3盒肉馅的“饺子”,3个三鲜馅的“饺子”和4个青菜馅的“饺子”.问:
(1)从甲箱中取出一盒“饺子”是肉馅的概率是多少?
(2)若依次从甲箱中取出两盒“饺了”,求第一盒是肉馅的条件下,第二盒是三鲜馅的概率;
(3)若先从甲箱中随机取出一盒“饺子”放入乙箱,再从乙箱中随机取出一盒“饺子”,从乙箱取出的“饺子”是肉馅的概率.
16.(15分)已知函数.
(1)求f(x)的最值;
(2)求曲线y=f(x)过点(0,2)的切线方程.
17.(15分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的20件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图(如图).
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的20件产品中任取3件,设X为质量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取5件产品,设Y为质量超过505克的产品数量,求Y的数学期望和方差.
18.(17分)已知双曲线C:经过点,右焦点为F(c,0),且c2,a2,b2成等差数列.
(1)求C的方程;
(2)过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,证明:是定值.
19.(17分)已知函数y=f(x)的定义域为区间D,若对于给定的非零实数m,存在x0,使得f(x0)=f(x0+m),则称函数y=f(x)在区间D上具有性质P(m).
(1)判断函数f(x)=x2在区间[﹣1,1]上是否具有性质P(),并说明理由;
(2)若函数f(x)=sinx在区间(0,n)(n>0)上具有性质P(),求n的取值范围;
(3)已知函数y=f(x)的图像是连续不断的曲线,且f(0)=f(2),求证:函数y=f(x)在区间[0,2]上具有性质P().
参考答案与试题解析
一、单选题:(本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的。
1.(5分)计算的值是( )
A.72 B.102 C.507 D.510
【解答】解:2+3=2+3=2×21+3×20=102.
故选:B.
2.(5分)已知等比数列{an}的公比为正数,且a3 a9=4a52,a2=1,则a1=( )
A.4 B.2 C.1 D.
【解答】解:设等比数列{an}的公比为q(q>0),
由a3 a9=4a,得a1q2 a1q8=4(a1q4)2,则q2=4,解得q=2,
又a2=1,所以a1==.
故选:D.
3.(5分)某校迎新晚会上有A,B,C,D,E,F共6个节目,为了考虑整体效果,对节目演出顺序有如下要求:节目A,B不相邻,节目D,F必须连在一起,则不同的节目编排方案种数为( )
A.60 B.72 C.120 D.144
【解答】解:先将两个节目D,F捆绑成一个元素,与节目C,E进行全排列,
再将节相A,B插入四个空档中,所以共有=144种不同的结果.
故选:D.
4.(5分)已知函数y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )
A. B.
C. D.
【解答】解:观察函数y=f(x)的图象知,
f(x)在(0,+∞)上是减函数,故y=f′(x)<0在(0,+∞)恒成立,故排除B,D,
f(x)在(﹣∞,0)从左到右,先增再减最后增,故y=f′(x)在(﹣∞,0)从左到右,先“+”再“﹣”最后“+”恒成立,故排除C,
故选:A.
5.(5分)设随机变量X服从两点分布,若P(X=1)﹣P(X=0)=0.4,则D(X)=( )
A.0.21 B.0.3 C.0.4 D.0.7
【解答】解:因为随机变量X服从两点分布,所以P(X=1)+P(X=0)=1,
又P(X=1)﹣P(X=0)=0.4,所以解得P(X=1)=0.7,P(X=0)=0.3,
所以E(X)=1×0.7+0×0.3=0.7,D(X)=(0﹣0.7)2×0.3+(1﹣0.7)2×0.7=0.21.
故选:A.
6.(5分)的展开式中,第四项和第五项的二项式系数相等,则该展开式中有理项的项数是( )
A.5 B.4 C.3 D.2
【解答】解:由于的展开式中,第四项和第五项的二项式系数相等,
故,故n=7.
所以=,
当r=0,2,4,6时,展开式为有理项,
故有理项的项数为4.
故选:B.
7.(5分)将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( )
A.420 B.180 C.64 D.25
【解答】解:方法一:由题意,由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行,
区域A有5种涂法,B有4种涂法,
A,D不同色,D有3种,C有2种涂法,有5×4×3×2=120种,
A,D同色,D有4种涂法,C有3种涂法,有5×4×3=60种,
∴共有180种不同的涂色方案.
方法二:分步,比如先排BCD,两两不同色,有5×4×3=60种,再排A,只要与BC不同,有3种,故共180种
故选:B.
8.(5分)已知实数a,b,c成公差非零的等差数列,集合A={(x,y)|ax+by+c=0},P(﹣3,2),N(2,3),M∈A,若∥(a,b),则|MN|的最大值是( )
A.4 B.5 C. D.
【解答】解:a、b、c成公差非零的等差数列,则2b=a+c,
动直线l:ax+by+c=0变形为a(2x+y)+c(y+2)=0,
令,解得,动直线l过定点Q(1,﹣2),
直线l:ax+by+c=0的一个法向量为=(a,b),
若∥(a,b),则MP⊥直线l,M点在以PQ为直径的圆上,
圆心为PQ中点C(﹣1,0),半径r=|PC|==2,|NC|==3,
则|MN|的最大值为32=5.
故选:D.
二、多选题:(本大题共3小题,每个小题6分,共18分.全部选对得6分,部分选对得3分,有选错的得0分.)
(多选)9.(6分)若P(A)=,P(B)=,P(B|A)=,则下列说法正确的是( )
A. B.事件A与B相互独立
C. D.
【解答】解:根据题意,依次分析选项:
对于A,P(B|A)=,变形可得P(AB)=P(A)P(B|A)=×=,A正确;
对于B,P(AB)≠P(A)P(B),则事件A、B不相互独立,B错误;
对于C,P(A∪B)=P(A)+P(B)﹣P(AB)=+﹣=,C正确;
对于D,P(B)=,P(AB)=P(A)P(B|A)=×=,
∴P(A|B)===,D正确.
故选:ACD.
(多选)10.(6分)在平面直角坐标系xOy中,过抛物线C:y2=4x的焦点F作直线l交抛物线C于A,B两点,则( )
A.|AB|的最小值为2
B.以线段AF为直径的圆与y轴相切
C.
D.
【解答】解:由题意可知:抛物线C:y2=4x的焦点F(1,0),准线为x=﹣1,
且直线l的斜率可以不存在,但不为0,
设直线l:x=my+1,A(x1,y1),B(x2,y2),
联立方程,消去x可得y2﹣4my﹣4=0,
则Δ=16m2+16>0,可得y1+y2=4m,y1y2=﹣4,
可得,
,
对于选项A:因为|AB|=4(m2+1)≥4,当且仅当m=0时,等号成立,
所以|AB|的最小值为4,故A错误;
对于选项B:因为线段AF的中点为,
则M到y轴的距离,以线段AF为直径的圆的半径为,
即圆心到y轴的距离等于该圆半径,故y轴与该圆相切,故B正确;
对于选项C:因为
=,
所以,故C正确;
对于选项D:因为=x1x2+y1y2=(my1+1)(my2+1)+y1y2
=(m2+1)y1y2+m(y1+y2)+1=﹣4(m2+1)+4m2+1=﹣3≠0,故D错误.
故选:BC.
(多选)11.(6分)若,则下列等式正确的有( )
A.a0=1
B.a3=160
C.a0+a2+a4+a6=365
D.a1+2a2+3a3+ +6a6=12
【解答】解:对于A,令x=﹣1,则,故A正确,
对于B,,因此,故B错误,
对于C,令x=0,则a0+a1+a2+a3+a4+a5+a6=1,令x=﹣2,则,两式相加可得,故C正确,
对于D,对两边求导得,
令x=0得a1+2a2+3a3+ +6a6=12,故D正确.
故选:ACD.
三、填空题:(本大题共3小题,每小题5分,共15分把答案填在答题卡中的横线上.)
12.(5分)的展开式中x2y6的系数为 ﹣28 (用数字作答).
【解答】解:由已知可得,
所以由二项式定理可得多项式的展开式中含x2y6的项为,
的展开式中x2y6的系数为﹣28.
故答案为:﹣28.
13.(5分)设F1,F2为椭圆的两个焦点,点P在椭圆C上,若,则|PF1| |PF2|= 2 .
【解答】解:已知点P在椭圆C上,且,可得,
又由椭圆,得c2=5﹣1=4,
|PF1|+|PF2|=2a=2,
∴,
而,可得|PF1| |PF2|=2.
故答案为:2.
14.(5分)设函数(a,b∈R)在区间[1,3]上总存在零点,则a2+b2的最小值为 .
【解答】解:设t为函数f(x)在区间[1,3]上的零点,
∵函数(a,b∈R)在区间[1,3]上总存在零点,
∴+a(t﹣1)+b=0,即(t﹣1)a+b+=0,
∴点P(a,b)是直线(t﹣1)x+y+=0上的点,
∴≥,化为:a2+b2≥,
令g(t)=,t∈[1,3],
则g′(x)==,
∵1≤t<2时,g′(x)<0;2<t≤3时,g′(x)>0.
∴函数g(t)在[1,2)上单调递减.在(2,3]上单调递增.
∴t=2时,函数g(t)取得极小值即最小值,g(2)=,
∴a2+b2≥,.
则a2+b2的最小值为.
故答案为:.
四、解答题:(本大题共5小题,共77分。解答应写出必要的文字说明、证明过程或演算步骤。)
15.(13分)中国传统文化中,过春节吃饺子,饺子是我国的传统美食,不仅味道鲜美而且寓意美好.现有甲、乙两个箱子装有大小、外观均相同的速冻饺子,已知甲箱中有3盒肉馅的“饺子”,2盒三鲜馅的“饺子”和5盒青菜馅的“饺子”,乙箱中有3盒肉馅的“饺子”,3个三鲜馅的“饺子”和4个青菜馅的“饺子”.问:
(1)从甲箱中取出一盒“饺子”是肉馅的概率是多少?
(2)若依次从甲箱中取出两盒“饺了”,求第一盒是肉馅的条件下,第二盒是三鲜馅的概率;
(3)若先从甲箱中随机取出一盒“饺子”放入乙箱,再从乙箱中随机取出一盒“饺子”,从乙箱取出的“饺子”是肉馅的概率.
【解答】解:(1)设事件A=“取出饺子是肉馅”,,
(2)设事件B=“甲箱中取出的第一盒饺子是肉馅”,
事件C=“取出第二个盒饺子是三鲜馅”,
(3)设事件D=“从乙箱取出的“饺子”是肉馅”.
设事件A1,A2,A3分别是甲箱中取出肉馅的“饺子”,三鲜馅的“饺子”和青菜馅的“饺子”,
P(D)=P(A1)P(D|A1)+P(A2)P(D|A2)+P(A3)P(D|A3)
=
16.(15分)已知函数.
(1)求f(x)的最值;
(2)求曲线y=f(x)过点(0,2)的切线方程.
【解答】解:(1)由已知可得,f(x)的定义域为(0,+∞),
且.
当0<x<2时,f′(x)<0,则f(x)在(0,2)上单调递减;
当x>2时,f′(x)>0,则f(x)在(2,+∞)上单调递增.
所以f(x)在x=2处取得唯一极小值,也是最小值.
所以f(x)的最小值为,无最大值.
(2)设切点为A(x0,y0),则
根据导数的几何意义可知,
曲线y=f(x)在A(x0,y0)处的斜率,
则=,
所以,
整理可得,.
设g(x)=x2+4lnx﹣1,则在(0,+∞)上恒成立,
所以g(x)在(0,+∞)上单调递增.
又g(1)=1+0﹣1=0,所以g(x)存在唯一解x=1.
所以的解为x0=1,切点A(1,0),
此时斜率为k=f′(1)=﹣2,
切线方程为y=﹣2(x﹣1),整理可得切线方程为2x+y﹣2=0.
17.(15分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的20件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图(如图).
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的20件产品中任取3件,设X为质量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取5件产品,设Y为质量超过505克的产品数量,求Y的数学期望和方差.
【解答】解:(1)质量超过505克的产品的频率为5×0.05+5×0.01=0.3,
所以质量超过505克的产品数量为20×0.3=6(件);
(2)重量超过505的产品数量为6件,则重量未超过505克的产品数量为14件,
X的取值可能为0,1,2,3,X服从超几何分布,
,
,
故X的分布列为:
X 0 1 2 3
P
(3)由质量超过505克的产品的频率为0.3,
故可估计从该流水线上任取1件产品质量超过505克的产品的概率为0.3,
从流水线上任取5件产品互不影响,该问题可看成5次独立重复试验,
即Y~B(5,0.3),
则E(Y)=5×0.3=1.5,D(Y)=5×0.3×(1﹣0.3)=1.05.
18.(17分)已知双曲线C:经过点,右焦点为F(c,0),且c2,a2,b2成等差数列.
(1)求C的方程;
(2)过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,证明:是定值.
【解答】解:(1)因为c2,a2,b2成等差数列,所以2a2=c2+b2,
又c2=a2+b2,所以a2=2b2.
将点的坐标代入C的方程得,解得b2=3,
所以a2=6,所以C的方程为.
(2)证明:依题意可设PQ:x=my+3,
由,得(m2﹣2)y2+6my+3=0,
设P(x1,y1),Q(x2,y2),y1>y2,则.
,,
则=,
而,
所以=,
所以是定值.
19.(17分)已知函数y=f(x)的定义域为区间D,若对于给定的非零实数m,存在x0,使得f(x0)=f(x0+m),则称函数y=f(x)在区间D上具有性质P(m).
(1)判断函数f(x)=x2在区间[﹣1,1]上是否具有性质P(),并说明理由;
(2)若函数f(x)=sinx在区间(0,n)(n>0)上具有性质P(),求n的取值范围;
(3)已知函数y=f(x)的图像是连续不断的曲线,且f(0)=f(2),求证:函数y=f(x)在区间[0,2]上具有性质P().
【解答】解:(1)函数f(x)=x2在区间[﹣1,1]上具有性质P(),
若,则,
因为﹣∈[﹣1,1],且﹣=∈[﹣1,1],
所以函数f(x)=x2在区间[﹣1,1]上具有性质P().
(2)由题意,存在x0∈(0,n),使得,
由正弦线的定义得(舍)或(k∈Z),
则得,
因为>0,所以k∈N,
又因为∈(0,n)且∈(0,n)(k∈N),
所以n,即所求n的取值范围是(,+∞).
证明:(3)设g(x)=f(x)﹣f(x+),x∈[0,],
则有g(0)=f(0)﹣f(),g()=f()﹣f(),g()=f()﹣f(1),…,g()=f()﹣f(),…,g()=f()﹣f(2),(k∈{1,2,3,…,6}),
以上各式相加得g(0)+g()+…+g()+…+g()=f(2)﹣f(0),
即g(0)+g()+…+g()+…+g()=0,
(i)当g(0)、g()、…、g()、…、g()中有一个为0时,不妨设g()=0,i∈{1,2,3,…,6},
即g()=f()﹣f()=0,即f()=f(+),i∈{1,2,3,…,6},
所以函数y=f(x)在区间[0,2]上具有性质P().
(ii)当g(0)、g()、…、g()、…、g()中均不为0时,由于其和为0,
则其中必存在正数和负数,不妨设g()>0,g()<0,
其中i≠j,i,j∈{1,2,3,…,6},
由于函数y=g(x)的图像是连续不断的曲线,所以当i<j时,至少存在一个实数x0(当i>j时,至少存在一个实数),
其中i,j∈{1,2,3,…,6},使得g(x0)=0,即,
即存在x0,使得,
所以函数y=f(x)在区间[0,2]上也具有性质P(),
综上所述,函数y=f(x)在区间[0,2]上具有性质P().
数学试题
一、单选题:(本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的。
1.(5分)计算的值是( )
A.72 B.102 C.507 D.510
2.(5分)已知等比数列{an}的公比为正数,且a3 a9=4a52,a2=1,则a1=( )
A.4 B.2 C.1 D.
3.(5分)某校迎新晚会上有A,B,C,D,E,F共6个节目,为了考虑整体效果,对节目演出顺序有如下要求:节目A,B不相邻,节目D,F必须连在一起,则不同的节目编排方案种数为( )
A.60 B.72 C.120 D.144
4.(5分)已知函数y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )
A. B.
C. D.
5.(5分)设随机变量X服从两点分布,若P(X=1)﹣P(X=0)=0.4,则D(X)=( )
A.0.21 B.0.3 C.0.4 D.0.7
6.(5分)的展开式中,第四项和第五项的二项式系数相等,则该展开式中有理项的项数是( )
A.5 B.4 C.3 D.2
7.(5分)将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( )
A.420 B.180 C.64 D.25
8.(5分)已知实数a,b,c成公差非零的等差数列,集合A={(x,y)|ax+by+c=0},P(﹣3,2),N(2,3),M∈A,若∥(a,b),则|MN|的最大值是( )
A.4 B.5 C. D.
二、多选题:(本大题共3小题,每个小题6分,共18分.全部选对得6分,部分选对得3分,有选错的得0分.)
(多选)9.(6分)若P(A)=,P(B)=,P(B|A)=,则下列说法正确的是( )
A. B.事件A与B相互独立
C. D.
(多选)10.(6分)在平面直角坐标系xOy中,过抛物线C:y2=4x的焦点F作直线l交抛物线C于A,B两点,则( )
A.|AB|的最小值为2
B.以线段AF为直径的圆与y轴相切
C.
D.
(多选)11.(6分)若,则下列等式正确的有( )
A.a0=1
B.a3=160
C.a0+a2+a4+a6=365
D.a1+2a2+3a3+ +6a6=12
三、填空题:(本大题共3小题,每小题5分,共15分把答案填在答题卡中的横线上.)
12.(5分)的展开式中x2y6的系数为 (用数字作答).
13.(5分)设F1,F2为椭圆的两个焦点,点P在椭圆C上,若,则|PF1| |PF2|= .
14.(5分)设函数(a,b∈R)在区间[1,3]上总存在零点,则a2+b2的最小值为 .
四、解答题:(本大题共5小题,共77分。解答应写出必要的文字说明、证明过程或演算步骤。)
15.(13分)中国传统文化中,过春节吃饺子,饺子是我国的传统美食,不仅味道鲜美而且寓意美好.现有甲、乙两个箱子装有大小、外观均相同的速冻饺子,已知甲箱中有3盒肉馅的“饺子”,2盒三鲜馅的“饺子”和5盒青菜馅的“饺子”,乙箱中有3盒肉馅的“饺子”,3个三鲜馅的“饺子”和4个青菜馅的“饺子”.问:
(1)从甲箱中取出一盒“饺子”是肉馅的概率是多少?
(2)若依次从甲箱中取出两盒“饺了”,求第一盒是肉馅的条件下,第二盒是三鲜馅的概率;
(3)若先从甲箱中随机取出一盒“饺子”放入乙箱,再从乙箱中随机取出一盒“饺子”,从乙箱取出的“饺子”是肉馅的概率.
16.(15分)已知函数.
(1)求f(x)的最值;
(2)求曲线y=f(x)过点(0,2)的切线方程.
17.(15分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的20件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图(如图).
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的20件产品中任取3件,设X为质量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取5件产品,设Y为质量超过505克的产品数量,求Y的数学期望和方差.
18.(17分)已知双曲线C:经过点,右焦点为F(c,0),且c2,a2,b2成等差数列.
(1)求C的方程;
(2)过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,证明:是定值.
19.(17分)已知函数y=f(x)的定义域为区间D,若对于给定的非零实数m,存在x0,使得f(x0)=f(x0+m),则称函数y=f(x)在区间D上具有性质P(m).
(1)判断函数f(x)=x2在区间[﹣1,1]上是否具有性质P(),并说明理由;
(2)若函数f(x)=sinx在区间(0,n)(n>0)上具有性质P(),求n的取值范围;
(3)已知函数y=f(x)的图像是连续不断的曲线,且f(0)=f(2),求证:函数y=f(x)在区间[0,2]上具有性质P().
参考答案与试题解析
一、单选题:(本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的。
1.(5分)计算的值是( )
A.72 B.102 C.507 D.510
【解答】解:2+3=2+3=2×21+3×20=102.
故选:B.
2.(5分)已知等比数列{an}的公比为正数,且a3 a9=4a52,a2=1,则a1=( )
A.4 B.2 C.1 D.
【解答】解:设等比数列{an}的公比为q(q>0),
由a3 a9=4a,得a1q2 a1q8=4(a1q4)2,则q2=4,解得q=2,
又a2=1,所以a1==.
故选:D.
3.(5分)某校迎新晚会上有A,B,C,D,E,F共6个节目,为了考虑整体效果,对节目演出顺序有如下要求:节目A,B不相邻,节目D,F必须连在一起,则不同的节目编排方案种数为( )
A.60 B.72 C.120 D.144
【解答】解:先将两个节目D,F捆绑成一个元素,与节目C,E进行全排列,
再将节相A,B插入四个空档中,所以共有=144种不同的结果.
故选:D.
4.(5分)已知函数y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )
A. B.
C. D.
【解答】解:观察函数y=f(x)的图象知,
f(x)在(0,+∞)上是减函数,故y=f′(x)<0在(0,+∞)恒成立,故排除B,D,
f(x)在(﹣∞,0)从左到右,先增再减最后增,故y=f′(x)在(﹣∞,0)从左到右,先“+”再“﹣”最后“+”恒成立,故排除C,
故选:A.
5.(5分)设随机变量X服从两点分布,若P(X=1)﹣P(X=0)=0.4,则D(X)=( )
A.0.21 B.0.3 C.0.4 D.0.7
【解答】解:因为随机变量X服从两点分布,所以P(X=1)+P(X=0)=1,
又P(X=1)﹣P(X=0)=0.4,所以解得P(X=1)=0.7,P(X=0)=0.3,
所以E(X)=1×0.7+0×0.3=0.7,D(X)=(0﹣0.7)2×0.3+(1﹣0.7)2×0.7=0.21.
故选:A.
6.(5分)的展开式中,第四项和第五项的二项式系数相等,则该展开式中有理项的项数是( )
A.5 B.4 C.3 D.2
【解答】解:由于的展开式中,第四项和第五项的二项式系数相等,
故,故n=7.
所以=,
当r=0,2,4,6时,展开式为有理项,
故有理项的项数为4.
故选:B.
7.(5分)将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( )
A.420 B.180 C.64 D.25
【解答】解:方法一:由题意,由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行,
区域A有5种涂法,B有4种涂法,
A,D不同色,D有3种,C有2种涂法,有5×4×3×2=120种,
A,D同色,D有4种涂法,C有3种涂法,有5×4×3=60种,
∴共有180种不同的涂色方案.
方法二:分步,比如先排BCD,两两不同色,有5×4×3=60种,再排A,只要与BC不同,有3种,故共180种
故选:B.
8.(5分)已知实数a,b,c成公差非零的等差数列,集合A={(x,y)|ax+by+c=0},P(﹣3,2),N(2,3),M∈A,若∥(a,b),则|MN|的最大值是( )
A.4 B.5 C. D.
【解答】解:a、b、c成公差非零的等差数列,则2b=a+c,
动直线l:ax+by+c=0变形为a(2x+y)+c(y+2)=0,
令,解得,动直线l过定点Q(1,﹣2),
直线l:ax+by+c=0的一个法向量为=(a,b),
若∥(a,b),则MP⊥直线l,M点在以PQ为直径的圆上,
圆心为PQ中点C(﹣1,0),半径r=|PC|==2,|NC|==3,
则|MN|的最大值为32=5.
故选:D.
二、多选题:(本大题共3小题,每个小题6分,共18分.全部选对得6分,部分选对得3分,有选错的得0分.)
(多选)9.(6分)若P(A)=,P(B)=,P(B|A)=,则下列说法正确的是( )
A. B.事件A与B相互独立
C. D.
【解答】解:根据题意,依次分析选项:
对于A,P(B|A)=,变形可得P(AB)=P(A)P(B|A)=×=,A正确;
对于B,P(AB)≠P(A)P(B),则事件A、B不相互独立,B错误;
对于C,P(A∪B)=P(A)+P(B)﹣P(AB)=+﹣=,C正确;
对于D,P(B)=,P(AB)=P(A)P(B|A)=×=,
∴P(A|B)===,D正确.
故选:ACD.
(多选)10.(6分)在平面直角坐标系xOy中,过抛物线C:y2=4x的焦点F作直线l交抛物线C于A,B两点,则( )
A.|AB|的最小值为2
B.以线段AF为直径的圆与y轴相切
C.
D.
【解答】解:由题意可知:抛物线C:y2=4x的焦点F(1,0),准线为x=﹣1,
且直线l的斜率可以不存在,但不为0,
设直线l:x=my+1,A(x1,y1),B(x2,y2),
联立方程,消去x可得y2﹣4my﹣4=0,
则Δ=16m2+16>0,可得y1+y2=4m,y1y2=﹣4,
可得,
,
对于选项A:因为|AB|=4(m2+1)≥4,当且仅当m=0时,等号成立,
所以|AB|的最小值为4,故A错误;
对于选项B:因为线段AF的中点为,
则M到y轴的距离,以线段AF为直径的圆的半径为,
即圆心到y轴的距离等于该圆半径,故y轴与该圆相切,故B正确;
对于选项C:因为
=,
所以,故C正确;
对于选项D:因为=x1x2+y1y2=(my1+1)(my2+1)+y1y2
=(m2+1)y1y2+m(y1+y2)+1=﹣4(m2+1)+4m2+1=﹣3≠0,故D错误.
故选:BC.
(多选)11.(6分)若,则下列等式正确的有( )
A.a0=1
B.a3=160
C.a0+a2+a4+a6=365
D.a1+2a2+3a3+ +6a6=12
【解答】解:对于A,令x=﹣1,则,故A正确,
对于B,,因此,故B错误,
对于C,令x=0,则a0+a1+a2+a3+a4+a5+a6=1,令x=﹣2,则,两式相加可得,故C正确,
对于D,对两边求导得,
令x=0得a1+2a2+3a3+ +6a6=12,故D正确.
故选:ACD.
三、填空题:(本大题共3小题,每小题5分,共15分把答案填在答题卡中的横线上.)
12.(5分)的展开式中x2y6的系数为 ﹣28 (用数字作答).
【解答】解:由已知可得,
所以由二项式定理可得多项式的展开式中含x2y6的项为,
的展开式中x2y6的系数为﹣28.
故答案为:﹣28.
13.(5分)设F1,F2为椭圆的两个焦点,点P在椭圆C上,若,则|PF1| |PF2|= 2 .
【解答】解:已知点P在椭圆C上,且,可得,
又由椭圆,得c2=5﹣1=4,
|PF1|+|PF2|=2a=2,
∴,
而,可得|PF1| |PF2|=2.
故答案为:2.
14.(5分)设函数(a,b∈R)在区间[1,3]上总存在零点,则a2+b2的最小值为 .
【解答】解:设t为函数f(x)在区间[1,3]上的零点,
∵函数(a,b∈R)在区间[1,3]上总存在零点,
∴+a(t﹣1)+b=0,即(t﹣1)a+b+=0,
∴点P(a,b)是直线(t﹣1)x+y+=0上的点,
∴≥,化为:a2+b2≥,
令g(t)=,t∈[1,3],
则g′(x)==,
∵1≤t<2时,g′(x)<0;2<t≤3时,g′(x)>0.
∴函数g(t)在[1,2)上单调递减.在(2,3]上单调递增.
∴t=2时,函数g(t)取得极小值即最小值,g(2)=,
∴a2+b2≥,.
则a2+b2的最小值为.
故答案为:.
四、解答题:(本大题共5小题,共77分。解答应写出必要的文字说明、证明过程或演算步骤。)
15.(13分)中国传统文化中,过春节吃饺子,饺子是我国的传统美食,不仅味道鲜美而且寓意美好.现有甲、乙两个箱子装有大小、外观均相同的速冻饺子,已知甲箱中有3盒肉馅的“饺子”,2盒三鲜馅的“饺子”和5盒青菜馅的“饺子”,乙箱中有3盒肉馅的“饺子”,3个三鲜馅的“饺子”和4个青菜馅的“饺子”.问:
(1)从甲箱中取出一盒“饺子”是肉馅的概率是多少?
(2)若依次从甲箱中取出两盒“饺了”,求第一盒是肉馅的条件下,第二盒是三鲜馅的概率;
(3)若先从甲箱中随机取出一盒“饺子”放入乙箱,再从乙箱中随机取出一盒“饺子”,从乙箱取出的“饺子”是肉馅的概率.
【解答】解:(1)设事件A=“取出饺子是肉馅”,,
(2)设事件B=“甲箱中取出的第一盒饺子是肉馅”,
事件C=“取出第二个盒饺子是三鲜馅”,
(3)设事件D=“从乙箱取出的“饺子”是肉馅”.
设事件A1,A2,A3分别是甲箱中取出肉馅的“饺子”,三鲜馅的“饺子”和青菜馅的“饺子”,
P(D)=P(A1)P(D|A1)+P(A2)P(D|A2)+P(A3)P(D|A3)
=
16.(15分)已知函数.
(1)求f(x)的最值;
(2)求曲线y=f(x)过点(0,2)的切线方程.
【解答】解:(1)由已知可得,f(x)的定义域为(0,+∞),
且.
当0<x<2时,f′(x)<0,则f(x)在(0,2)上单调递减;
当x>2时,f′(x)>0,则f(x)在(2,+∞)上单调递增.
所以f(x)在x=2处取得唯一极小值,也是最小值.
所以f(x)的最小值为,无最大值.
(2)设切点为A(x0,y0),则
根据导数的几何意义可知,
曲线y=f(x)在A(x0,y0)处的斜率,
则=,
所以,
整理可得,.
设g(x)=x2+4lnx﹣1,则在(0,+∞)上恒成立,
所以g(x)在(0,+∞)上单调递增.
又g(1)=1+0﹣1=0,所以g(x)存在唯一解x=1.
所以的解为x0=1,切点A(1,0),
此时斜率为k=f′(1)=﹣2,
切线方程为y=﹣2(x﹣1),整理可得切线方程为2x+y﹣2=0.
17.(15分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的20件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图(如图).
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的20件产品中任取3件,设X为质量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取5件产品,设Y为质量超过505克的产品数量,求Y的数学期望和方差.
【解答】解:(1)质量超过505克的产品的频率为5×0.05+5×0.01=0.3,
所以质量超过505克的产品数量为20×0.3=6(件);
(2)重量超过505的产品数量为6件,则重量未超过505克的产品数量为14件,
X的取值可能为0,1,2,3,X服从超几何分布,
,
,
故X的分布列为:
X 0 1 2 3
P
(3)由质量超过505克的产品的频率为0.3,
故可估计从该流水线上任取1件产品质量超过505克的产品的概率为0.3,
从流水线上任取5件产品互不影响,该问题可看成5次独立重复试验,
即Y~B(5,0.3),
则E(Y)=5×0.3=1.5,D(Y)=5×0.3×(1﹣0.3)=1.05.
18.(17分)已知双曲线C:经过点,右焦点为F(c,0),且c2,a2,b2成等差数列.
(1)求C的方程;
(2)过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,证明:是定值.
【解答】解:(1)因为c2,a2,b2成等差数列,所以2a2=c2+b2,
又c2=a2+b2,所以a2=2b2.
将点的坐标代入C的方程得,解得b2=3,
所以a2=6,所以C的方程为.
(2)证明:依题意可设PQ:x=my+3,
由,得(m2﹣2)y2+6my+3=0,
设P(x1,y1),Q(x2,y2),y1>y2,则.
,,
则=,
而,
所以=,
所以是定值.
19.(17分)已知函数y=f(x)的定义域为区间D,若对于给定的非零实数m,存在x0,使得f(x0)=f(x0+m),则称函数y=f(x)在区间D上具有性质P(m).
(1)判断函数f(x)=x2在区间[﹣1,1]上是否具有性质P(),并说明理由;
(2)若函数f(x)=sinx在区间(0,n)(n>0)上具有性质P(),求n的取值范围;
(3)已知函数y=f(x)的图像是连续不断的曲线,且f(0)=f(2),求证:函数y=f(x)在区间[0,2]上具有性质P().
【解答】解:(1)函数f(x)=x2在区间[﹣1,1]上具有性质P(),
若,则,
因为﹣∈[﹣1,1],且﹣=∈[﹣1,1],
所以函数f(x)=x2在区间[﹣1,1]上具有性质P().
(2)由题意,存在x0∈(0,n),使得,
由正弦线的定义得(舍)或(k∈Z),
则得,
因为>0,所以k∈N,
又因为∈(0,n)且∈(0,n)(k∈N),
所以n,即所求n的取值范围是(,+∞).
证明:(3)设g(x)=f(x)﹣f(x+),x∈[0,],
则有g(0)=f(0)﹣f(),g()=f()﹣f(),g()=f()﹣f(1),…,g()=f()﹣f(),…,g()=f()﹣f(2),(k∈{1,2,3,…,6}),
以上各式相加得g(0)+g()+…+g()+…+g()=f(2)﹣f(0),
即g(0)+g()+…+g()+…+g()=0,
(i)当g(0)、g()、…、g()、…、g()中有一个为0时,不妨设g()=0,i∈{1,2,3,…,6},
即g()=f()﹣f()=0,即f()=f(+),i∈{1,2,3,…,6},
所以函数y=f(x)在区间[0,2]上具有性质P().
(ii)当g(0)、g()、…、g()、…、g()中均不为0时,由于其和为0,
则其中必存在正数和负数,不妨设g()>0,g()<0,
其中i≠j,i,j∈{1,2,3,…,6},
由于函数y=g(x)的图像是连续不断的曲线,所以当i<j时,至少存在一个实数x0(当i>j时,至少存在一个实数),
其中i,j∈{1,2,3,…,6},使得g(x0)=0,即,
即存在x0,使得,
所以函数y=f(x)在区间[0,2]上也具有性质P(),
综上所述,函数y=f(x)在区间[0,2]上具有性质P().
同课章节目录
