9.2 一元一次不等式 课件(共15张PPT)2023-2024学年人教版数学七年级下册
文档属性
| 名称 | 9.2 一元一次不等式 课件(共15张PPT)2023-2024学年人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第九章
不等式与不等式组
9.2一元一次不等式
学习目标
观察下面的等式,它们有哪些共同特征?
1.只含有1个未知数
2.未知数的次数都是1.
3.等式两边都是整式
的方程
复习与回顾
观察下面的不等式,它们有哪些共同特征?
1.只含有1个未知数
2.未知数的次数都是1.
3.不等式两边都是整 式
学习新知
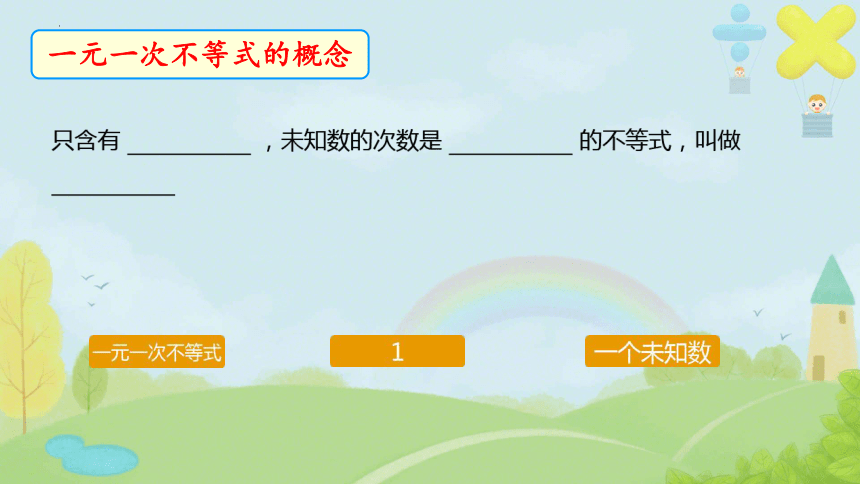
一元一次不等式的概念
自学检测
1、若是关于x的一元一次不等式 ,
则m=____。
∵|m|=1
又∵ m+1≠0
∴m≠-1
∴m=1
1
解一元一次不等式,要根据____________,将不等式逐步
化为___________的形式。
二
解一元一方程
依据:
等式的性质2
合并同类项法则
等式的性质2
解一元一次方程,要根据___________,将方程逐步化为x=a的形式。
等式的性质
不等式的性质
x>a或x解:去分母:
3(2+x)= 2(2x-1)
去括号:
6+3x=4x-2
移项:
3x-4x=-2-6
合并同类项:
-x=-8
系数化为1 :
x = 8
去括号法则
等式的性质1
解一元一不等式
解方程
解:
解一元一次不等式
依据:
等式的
性质2
合并同类项法则
等式的性质2
3(2+x)= 2(2x-1)
6+3x=4x-2
3x-4x=-2-6
-x=-8
x = 8
去括号法则
等式的性质1
3(2+x)> 2(2x-1)
6+3x > 4x-2
3x-4x > -2-6
-x > -8
x < 8
解:
自学检测
解一元一次不等式,要根据不等式的性质,将不等式逐步化为x>a或x解:
移项,得:
合并同类项,得:
系数化为1, 得:
解:
去括号,得:
移项,得:
合并同类项, 得:
系数化为1, 得:
2、解下列不等式:
3、解下列不等式,并在数轴上表示解集:
(1) (2)
自学检测
数轴表示不等式解集的口诀:1.有等号实心,无等号空心
2.大于号右转,小于号左转
3(x-1)< 7(2x+5)
3x-3<14x+35
3x-14x<35+3
-11x<38
x>
解:
2(x+1)≥3(2x-5)+1×12
2x+2≥6x-15+12
2x-6x≥-15+12-2
-4x ≥-5
x≤
解:
1.去分母
2.去括号
3.移项
4.合并同类项
5.系数化为1
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
注意:系数化为1时,遇到负数则要变号
更正讨论
解一元一次不等式的步骤是什么?解一元一次不等式的依据是什么?需要特别注意什么?
当堂训练
1、当x为何值时,式子 的值不小于 的值?
解:
由题意得
综上:
满足题意
当堂训练
2、求不等式 的非正整数解。
解:
∴满足条件的非正整数解有:
-4,-3,-2,-1。
思维拓展
1、已知关于x,y的方程组 的解满足x①
②
解:
由题意得
①+②得
x-y+2x+y=a+3+5a
3x=6a+3
x=2a+1
将x=2a+1带入①当中得
2a+1-y=a+3
y=a-2
∵ x < y
∴ 2a+1 < a-2
2a-a < -2-1
a < -3
综上: a<-3
第九章
不等式与不等式组
9.2一元一次不等式
学习目标
观察下面的等式,它们有哪些共同特征?
1.只含有1个未知数
2.未知数的次数都是1.
3.等式两边都是整式
的方程
复习与回顾
观察下面的不等式,它们有哪些共同特征?
1.只含有1个未知数
2.未知数的次数都是1.
3.不等式两边都是整 式
学习新知
一元一次不等式的概念
自学检测
1、若是关于x的一元一次不等式 ,
则m=____。
∵|m|=1
又∵ m+1≠0
∴m≠-1
∴m=1
1
解一元一次不等式,要根据____________,将不等式逐步
化为___________的形式。
二
解一元一方程
依据:
等式的性质2
合并同类项法则
等式的性质2
解一元一次方程,要根据___________,将方程逐步化为x=a的形式。
等式的性质
不等式的性质
x>a或x
3(2+x)= 2(2x-1)
去括号:
6+3x=4x-2
移项:
3x-4x=-2-6
合并同类项:
-x=-8
系数化为1 :
x = 8
去括号法则
等式的性质1
解一元一不等式
解方程
解:
解一元一次不等式
依据:
等式的
性质2
合并同类项法则
等式的性质2
3(2+x)= 2(2x-1)
6+3x=4x-2
3x-4x=-2-6
-x=-8
x = 8
去括号法则
等式的性质1
3(2+x)> 2(2x-1)
6+3x > 4x-2
3x-4x > -2-6
-x > -8
x < 8
解:
自学检测
解一元一次不等式,要根据不等式的性质,将不等式逐步化为x>a或x
移项,得:
合并同类项,得:
系数化为1, 得:
解:
去括号,得:
移项,得:
合并同类项, 得:
系数化为1, 得:
2、解下列不等式:
3、解下列不等式,并在数轴上表示解集:
(1) (2)
自学检测
数轴表示不等式解集的口诀:1.有等号实心,无等号空心
2.大于号右转,小于号左转
3(x-1)< 7(2x+5)
3x-3<14x+35
3x-14x<35+3
-11x<38
x>
解:
2(x+1)≥3(2x-5)+1×12
2x+2≥6x-15+12
2x-6x≥-15+12-2
-4x ≥-5
x≤
解:
1.去分母
2.去括号
3.移项
4.合并同类项
5.系数化为1
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
注意:系数化为1时,遇到负数则要变号
更正讨论
解一元一次不等式的步骤是什么?解一元一次不等式的依据是什么?需要特别注意什么?
当堂训练
1、当x为何值时,式子 的值不小于 的值?
解:
由题意得
综上:
满足题意
当堂训练
2、求不等式 的非正整数解。
解:
∴满足条件的非正整数解有:
-4,-3,-2,-1。
思维拓展
1、已知关于x,y的方程组 的解满足x
②
解:
由题意得
①+②得
x-y+2x+y=a+3+5a
3x=6a+3
x=2a+1
将x=2a+1带入①当中得
2a+1-y=a+3
y=a-2
∵ x < y
∴ 2a+1 < a-2
2a-a < -2-1
a < -3
综上: a<-3
