5.1 相交线 教学设计 2023--2024学年人教版七年级数学下册
文档属性
| 名称 | 5.1 相交线 教学设计 2023--2024学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 18:41:31 | ||
图片预览

文档简介
5.1 相交线
5.1.1 相交线
教学目标
1、 知识与技能:表述对顶角、邻补角的概念、性质,并能利用它进行简单
的推理和计算,通过对顶角性质的推理过程,提高推理和逻辑思维能力,通过变
式图形的识图训练,提高识图能力
2、过程与方法:经历实际操作,通过观察讨论等活动,能在具体的情境中
认识对顶角、邻补角。
3、情感态度价值观:从图形变化过程中,树立正确的辩证唯物主义观点,
认识儿何图形的位置美
教学重点 邻补角、对顶角的概念,对顶角性质与应用.
教学难点 理解对顶角相等的性质的探索
教学过程
情景导入(PPT展示图片)
纵横交错的道路,棋盘中的横线和竖线以及操场上的双杠----都给我们以相交线或平行线的形象,请大家再举出一些相交线和平行线的实例,小组内交流。
我们生活的世界中,蕴涵着大量的相交线和平行线,这节课我们就来研究两条直线相交所成的角的位置关系和数量关系。
出示学习目标
能准确识别邻补角与对顶角.
掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.
出示自学指导
自学课本2、3页内容
组内讨论、答疑
3. 领学人组织课堂学习
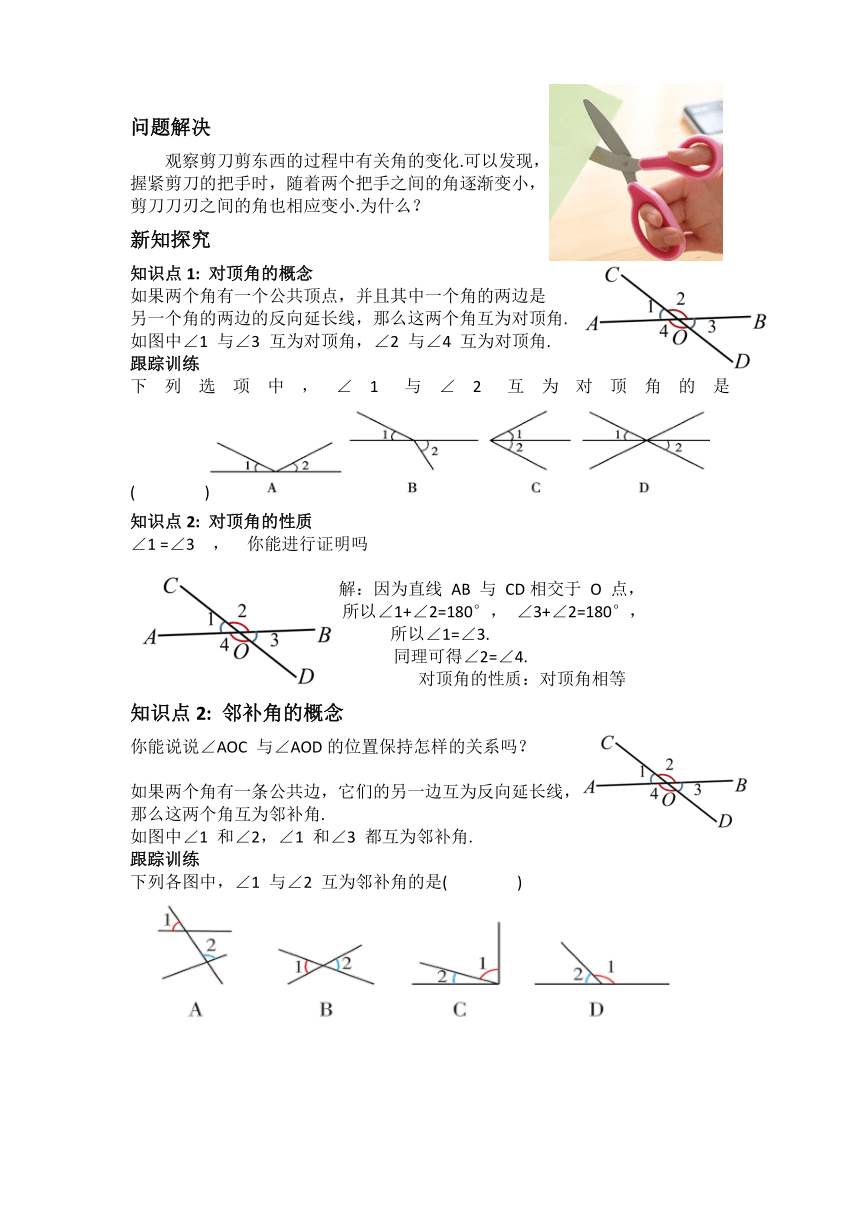
问题解决
观察剪刀剪东西的过程中有关角的变化.可以发现,
握紧剪刀的把手时,随着两个把手之间的角逐渐变小,
剪刀刀刃之间的角也相应变小.为什么?
新知探究
知识点1: 对顶角的概念
如果两个角有一个公共顶点,并且其中一个角的两边是
另一个角的两边的反向延长线,那么这两个角互为对顶角.
如图中∠1 与∠3 互为对顶角,∠2 与∠4 互为对顶角.
跟踪训练
下列选项中,∠1 与∠2 互为对顶角的是( )
知识点2: 对顶角的性质
∠1 =∠3 , 你能进行证明吗
解:因为直线 AB 与 CD相交于 O 点,
所以∠1+∠2=180°, ∠3+∠2=180°,
所以∠1=∠3.
同理可得∠2=∠4.
对顶角的性质:对顶角相等
知识点2: 邻补角的概念
你能说说∠AOC 与∠AOD的位置保持怎样的关系吗?
如果两个角有一条公共边,它们的另一边互为反向延长线,
那么这两个角互为邻补角.
如图中∠1 和∠2,∠1 和∠3 都互为邻补角.
跟踪训练
下列各图中,∠1 与∠2 互为邻补角的是( )
知识点3:区别对顶角与邻补角
对顶角 邻补角
相同点 ①都是两条直线相交而成的角②都有一个公共顶点③都是成对出现的
不同点 无公共边 有一条无公共边
两直线相交时,对顶角只有两对 两直线相交时,邻补角有四对
对顶角相等 邻补角互补
运用新知
1.图中是对顶角量角器,你能说出用它测量角的
度数的原理吗?
2. 如图,直线 a,b 相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
随堂练习
下列各图中1,∠1和∠2是邻补角吗?
(
图
2
) (
图
1
)
2.如图2,下列各组角中,互为对顶角的是( )
A. ∠1和∠2 B. ∠1和∠3 C. ∠2和∠4 D. ∠2和∠5
(
图
4
) (
图
3
)
3.如图3,三条直线 l1 ,l2,l3 相交于一点,则∠1+∠2+∠3 等于( )
A.90° B.120° C.180° D.360°
4.如图4,AB 与 CD 相交于点 O,OE 是 ∠AOC 的平分线,且 OC 恰好平分
∠EOB,则∠AOD = ( )度
课堂小结
回顾本节课的学习内容,想想都学习了哪些新知识?又是怎么运用的?运用时要注意什么?谈谈你的收获,小组内交流。
当堂测试
1.如图5.1.1-8,下列各组角中,是对顶角的一组是( )
A. ∠1和∠2 B. ∠3和∠5 C∠3和∠4 D. ∠1 和∠5
如图 5.1.1-9,点O在直线 AB 上,射线 OC平分∠DOB.若∠COB =35°,
则∠AOD 等于( )
A. 35° B.70° C.110° D.145°
3.如图5.1.1-10,已知∠a十∠B=80°,则∠a=——
4.如图 5.1.1-11,直线 AB,CD 相交于点O,若∠1-∠2=70°, ∠ BOC=——,∠2=——
5.如图 5.1.1-12 所示,直线 AB,CD,EF 相交于O,若∠1=20°,∠BOC=80°,求∠2的度数。
课后作业
必做题: 1.课本第7页习题5.1:1、2题
2.预习5.1.2 垂线
选做题:课本第8页第8题
教学反思
本节课的设计以学生熟悉的生活实例为情景引入课题,遵循了从具体到抽象,从感性到理性的渐进的认知规律,不仅可以增强学生的学习兴趣,还可以让学生增强对相交线和平行线的生活原型的认识,从而建立直观形象的数学模型
本节课是在学习了基本平面图形直线、射线、线段、角之后,进一步研究平面内两直线相交的情形,在教学过程中,给学生充分的合作交流、自主学习的时间和空间,让学生与学生的交流合作在探究过程中进行,使他们在自主探索的过程中理解和掌握邻补角、对顶角的概念、性质,并获得数学活动的经验,提高探究、发现和创新的能力。
5.1.1 相交线
教学目标
1、 知识与技能:表述对顶角、邻补角的概念、性质,并能利用它进行简单
的推理和计算,通过对顶角性质的推理过程,提高推理和逻辑思维能力,通过变
式图形的识图训练,提高识图能力
2、过程与方法:经历实际操作,通过观察讨论等活动,能在具体的情境中
认识对顶角、邻补角。
3、情感态度价值观:从图形变化过程中,树立正确的辩证唯物主义观点,
认识儿何图形的位置美
教学重点 邻补角、对顶角的概念,对顶角性质与应用.
教学难点 理解对顶角相等的性质的探索
教学过程
情景导入(PPT展示图片)
纵横交错的道路,棋盘中的横线和竖线以及操场上的双杠----都给我们以相交线或平行线的形象,请大家再举出一些相交线和平行线的实例,小组内交流。
我们生活的世界中,蕴涵着大量的相交线和平行线,这节课我们就来研究两条直线相交所成的角的位置关系和数量关系。
出示学习目标
能准确识别邻补角与对顶角.
掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.
出示自学指导
自学课本2、3页内容
组内讨论、答疑
3. 领学人组织课堂学习
问题解决
观察剪刀剪东西的过程中有关角的变化.可以发现,
握紧剪刀的把手时,随着两个把手之间的角逐渐变小,
剪刀刀刃之间的角也相应变小.为什么?
新知探究
知识点1: 对顶角的概念
如果两个角有一个公共顶点,并且其中一个角的两边是
另一个角的两边的反向延长线,那么这两个角互为对顶角.
如图中∠1 与∠3 互为对顶角,∠2 与∠4 互为对顶角.
跟踪训练
下列选项中,∠1 与∠2 互为对顶角的是( )
知识点2: 对顶角的性质
∠1 =∠3 , 你能进行证明吗
解:因为直线 AB 与 CD相交于 O 点,
所以∠1+∠2=180°, ∠3+∠2=180°,
所以∠1=∠3.
同理可得∠2=∠4.
对顶角的性质:对顶角相等
知识点2: 邻补角的概念
你能说说∠AOC 与∠AOD的位置保持怎样的关系吗?
如果两个角有一条公共边,它们的另一边互为反向延长线,
那么这两个角互为邻补角.
如图中∠1 和∠2,∠1 和∠3 都互为邻补角.
跟踪训练
下列各图中,∠1 与∠2 互为邻补角的是( )
知识点3:区别对顶角与邻补角
对顶角 邻补角
相同点 ①都是两条直线相交而成的角②都有一个公共顶点③都是成对出现的
不同点 无公共边 有一条无公共边
两直线相交时,对顶角只有两对 两直线相交时,邻补角有四对
对顶角相等 邻补角互补
运用新知
1.图中是对顶角量角器,你能说出用它测量角的
度数的原理吗?
2. 如图,直线 a,b 相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
随堂练习
下列各图中1,∠1和∠2是邻补角吗?
(
图
2
) (
图
1
)
2.如图2,下列各组角中,互为对顶角的是( )
A. ∠1和∠2 B. ∠1和∠3 C. ∠2和∠4 D. ∠2和∠5
(
图
4
) (
图
3
)
3.如图3,三条直线 l1 ,l2,l3 相交于一点,则∠1+∠2+∠3 等于( )
A.90° B.120° C.180° D.360°
4.如图4,AB 与 CD 相交于点 O,OE 是 ∠AOC 的平分线,且 OC 恰好平分
∠EOB,则∠AOD = ( )度
课堂小结
回顾本节课的学习内容,想想都学习了哪些新知识?又是怎么运用的?运用时要注意什么?谈谈你的收获,小组内交流。
当堂测试
1.如图5.1.1-8,下列各组角中,是对顶角的一组是( )
A. ∠1和∠2 B. ∠3和∠5 C∠3和∠4 D. ∠1 和∠5
如图 5.1.1-9,点O在直线 AB 上,射线 OC平分∠DOB.若∠COB =35°,
则∠AOD 等于( )
A. 35° B.70° C.110° D.145°
3.如图5.1.1-10,已知∠a十∠B=80°,则∠a=——
4.如图 5.1.1-11,直线 AB,CD 相交于点O,若∠1-∠2=70°, ∠ BOC=——,∠2=——
5.如图 5.1.1-12 所示,直线 AB,CD,EF 相交于O,若∠1=20°,∠BOC=80°,求∠2的度数。
课后作业
必做题: 1.课本第7页习题5.1:1、2题
2.预习5.1.2 垂线
选做题:课本第8页第8题
教学反思
本节课的设计以学生熟悉的生活实例为情景引入课题,遵循了从具体到抽象,从感性到理性的渐进的认知规律,不仅可以增强学生的学习兴趣,还可以让学生增强对相交线和平行线的生活原型的认识,从而建立直观形象的数学模型
本节课是在学习了基本平面图形直线、射线、线段、角之后,进一步研究平面内两直线相交的情形,在教学过程中,给学生充分的合作交流、自主学习的时间和空间,让学生与学生的交流合作在探究过程中进行,使他们在自主探索的过程中理解和掌握邻补角、对顶角的概念、性质,并获得数学活动的经验,提高探究、发现和创新的能力。
