第五章 相交线与平行线 复习练习题 (含答案) 2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 第五章 相交线与平行线 复习练习题 (含答案) 2023-2024学年人教版七年级数学下册 | 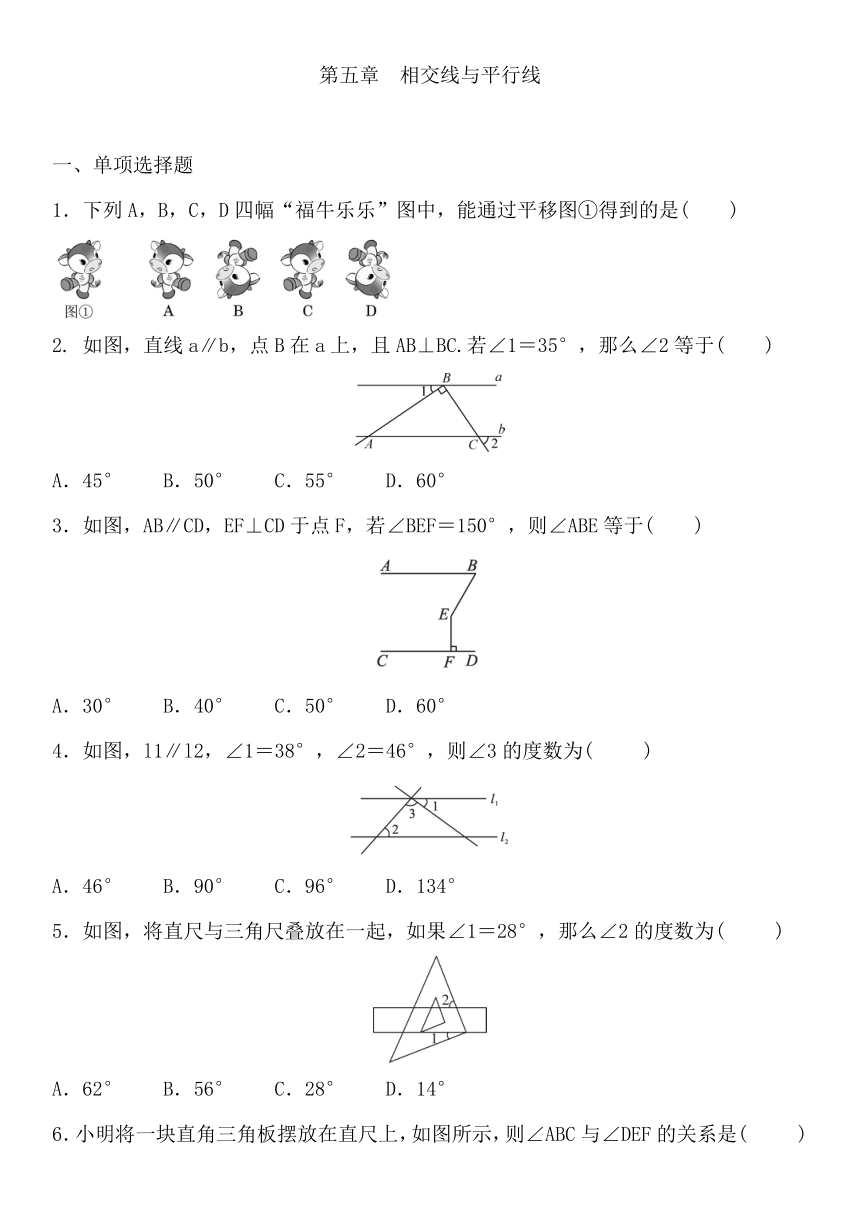 | |
| 格式 | docx | ||
| 文件大小 | 495.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 18:48:21 | ||
图片预览



文档简介
第五章 相交线与平行线
一、单项选择题
1.下列A,B,C,D四幅“福牛乐乐”图中,能通过平移图①得到的是( )
2. 如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45° B.50° C.55° D.60°
3.如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE等于( )
A.30° B.40° C.50° D.60°
4.如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A.46° B.90° C.96° D.134°
5.如图,将直尺与三角尺叠放在一起,如果∠1=28°,那么∠2的度数为( )
A.62° B.56° C.28° D.14°
6.小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
7.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
8.如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=12,DH=6,平移距离为7,则阴影部分的面积为( )
A.63 B.54 C.52 D.50
二、填空题
8.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=____.
10.如图,已知AE∥BD,AC、BD相交于点F,若∠1=3∠2,∠2=25°,则∠C=____.
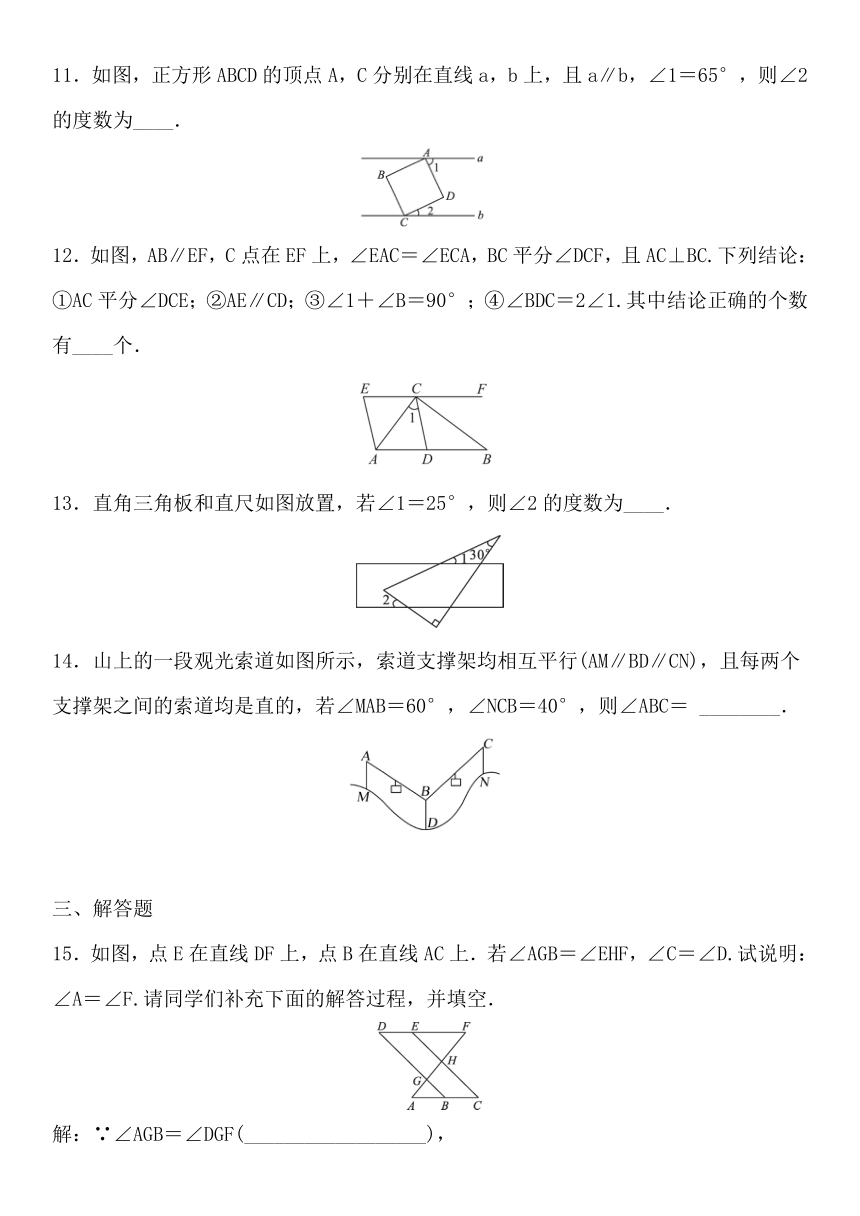
11.如图,正方形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=65°,则∠2的度数为____.
12.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC⊥BC.下列结论:①AC平分∠DCE;②AE∥CD;③∠1+∠B=90°;④∠BDC=2∠1.其中结论正确的个数有____个.
13.直角三角板和直尺如图放置,若∠1=25°,则∠2的度数为____.
14.山上的一段观光索道如图所示,索道支撑架均相互平行(AM∥BD∥CN),且每两个支撑架之间的索道均是直的,若∠MAB=60°,∠NCB=40°,则∠ABC= ________.
三、解答题
15.如图,点E在直线DF上,点B在直线AC上.若∠AGB=∠EHF,∠C=∠D.试说明:∠A=∠F.请同学们补充下面的解答过程,并填空.
解:∵∠AGB=∠DGF(__________________),
∠AGB=∠EHF(__________),
∴∠DGF=∠EHF.
∴DB∥EC(_______________________________).
∴∠D=_______________(两直线平行,同位角相等).
∵∠D=∠C(__________),
∴______________=C.
∴DF∥__________(__________________________).
∴∠A=∠F(______________________________).
16.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,求∠AOF的度数.
17.如图,∠BAF=46°,∠ACE=136°,CE⊥CD,CD与AB平行吗?为什么?
18.如图,BD∥EF,AE与BD交于点C,∠B=36°,∠A=72°,∠DEF=∠CEF,判断AB与DE是否平行,并说明理由.
19.如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.试说明:AB∥CD,EG∥FH.
20.如图所示,已知BA平分∠EBC,CD平分∠ACF,且AB∥CD.
(1)试判断AC与BE的位置关系,并说明理由;
(2)若DC⊥EC,垂足为C,猜想∠E与∠FCD之间的关系,并说明理由.
答案
一、
1-8 CCDCA ACA
二、
9. 360°
10. 50°
11. 25°
12. 4
13. 35°
14. 100°
三、
15. 对顶角相等
已知
同位角相等,两直线平行
∠FEH
已知
∠FEH
AC 内错角相等,两直线平行
两直线平行,内错角相等
16. 解:∵CD∥AB,∴∠AOD+∠D=180°,∴∠AOD=70°,∴∠DOB=110°.
∵OE平分∠BOD,∴∠DOE=55°.∵OF⊥OE,∴∠FOE=90°,
∴∠DOF=90°-55°=35°,∴∠AOF=70°-35°=35°
17. 解:CD∥AB.理由:∵CE⊥CD,∴∠DCE=90°.∵∠ACE=136°,
∴∠ACD=360°-136°-90°=134°.∵∠BAF=46°,
∴∠BAC=180°-∠BAF=180°-46°=134°,∴∠ACD=∠BAC,∴CD∥AB
18. 解:AB∥DE,理由如下:∵BD∥EF,∴∠CEF=∠ACD=180°-∠ACB,
又∵∠A+∠B+∠ACB=180°且∠A=72°,∠B=36°,∴∠ACB=72°,
∴∠CEF=∠ACD=180°-∠ACB=108°,∴∠D=∠DEF=∠CEF=36°=∠B,
∴AB∥DE
19. 解:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,
∴∠FCD=∠3,∴AB∥CD,∵∠2=50°,
∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,
∴∠GEF=∠NEF=65°,∴∠GEF=∠3,∴EG∥FH
20. 解:(1)AC∥BE,理由:∵BA平分∠EBC,CD平分∠ACF,
∴∠EBC=2∠CBA,∠ACF=2∠FCD,∵AB∥CD,∴∠CBA=∠FCD,
∴∠EBC=∠ACF,∴AC∥BE
(2)∠E与∠FCD互余,理由为:∵AC∥BE,∴∠E=∠ACE,
∵CD平分∠ACF,∴∠ACD=∠FCD,∵DC⊥EC,∴∠ACE+∠ACD=90°,
∴∠E+∠FCD=90°,即∠E与∠FCD互余
一、单项选择题
1.下列A,B,C,D四幅“福牛乐乐”图中,能通过平移图①得到的是( )
2. 如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45° B.50° C.55° D.60°
3.如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE等于( )
A.30° B.40° C.50° D.60°
4.如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A.46° B.90° C.96° D.134°
5.如图,将直尺与三角尺叠放在一起,如果∠1=28°,那么∠2的度数为( )
A.62° B.56° C.28° D.14°
6.小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
7.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
8.如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=12,DH=6,平移距离为7,则阴影部分的面积为( )
A.63 B.54 C.52 D.50
二、填空题
8.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=____.
10.如图,已知AE∥BD,AC、BD相交于点F,若∠1=3∠2,∠2=25°,则∠C=____.
11.如图,正方形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=65°,则∠2的度数为____.
12.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC⊥BC.下列结论:①AC平分∠DCE;②AE∥CD;③∠1+∠B=90°;④∠BDC=2∠1.其中结论正确的个数有____个.
13.直角三角板和直尺如图放置,若∠1=25°,则∠2的度数为____.
14.山上的一段观光索道如图所示,索道支撑架均相互平行(AM∥BD∥CN),且每两个支撑架之间的索道均是直的,若∠MAB=60°,∠NCB=40°,则∠ABC= ________.
三、解答题
15.如图,点E在直线DF上,点B在直线AC上.若∠AGB=∠EHF,∠C=∠D.试说明:∠A=∠F.请同学们补充下面的解答过程,并填空.
解:∵∠AGB=∠DGF(__________________),
∠AGB=∠EHF(__________),
∴∠DGF=∠EHF.
∴DB∥EC(_______________________________).
∴∠D=_______________(两直线平行,同位角相等).
∵∠D=∠C(__________),
∴______________=C.
∴DF∥__________(__________________________).
∴∠A=∠F(______________________________).
16.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,求∠AOF的度数.
17.如图,∠BAF=46°,∠ACE=136°,CE⊥CD,CD与AB平行吗?为什么?
18.如图,BD∥EF,AE与BD交于点C,∠B=36°,∠A=72°,∠DEF=∠CEF,判断AB与DE是否平行,并说明理由.
19.如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.试说明:AB∥CD,EG∥FH.
20.如图所示,已知BA平分∠EBC,CD平分∠ACF,且AB∥CD.
(1)试判断AC与BE的位置关系,并说明理由;
(2)若DC⊥EC,垂足为C,猜想∠E与∠FCD之间的关系,并说明理由.
答案
一、
1-8 CCDCA ACA
二、
9. 360°
10. 50°
11. 25°
12. 4
13. 35°
14. 100°
三、
15. 对顶角相等
已知
同位角相等,两直线平行
∠FEH
已知
∠FEH
AC 内错角相等,两直线平行
两直线平行,内错角相等
16. 解:∵CD∥AB,∴∠AOD+∠D=180°,∴∠AOD=70°,∴∠DOB=110°.
∵OE平分∠BOD,∴∠DOE=55°.∵OF⊥OE,∴∠FOE=90°,
∴∠DOF=90°-55°=35°,∴∠AOF=70°-35°=35°
17. 解:CD∥AB.理由:∵CE⊥CD,∴∠DCE=90°.∵∠ACE=136°,
∴∠ACD=360°-136°-90°=134°.∵∠BAF=46°,
∴∠BAC=180°-∠BAF=180°-46°=134°,∴∠ACD=∠BAC,∴CD∥AB
18. 解:AB∥DE,理由如下:∵BD∥EF,∴∠CEF=∠ACD=180°-∠ACB,
又∵∠A+∠B+∠ACB=180°且∠A=72°,∠B=36°,∴∠ACB=72°,
∴∠CEF=∠ACD=180°-∠ACB=108°,∴∠D=∠DEF=∠CEF=36°=∠B,
∴AB∥DE
19. 解:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,
∴∠FCD=∠3,∴AB∥CD,∵∠2=50°,
∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,
∴∠GEF=∠NEF=65°,∴∠GEF=∠3,∴EG∥FH
20. 解:(1)AC∥BE,理由:∵BA平分∠EBC,CD平分∠ACF,
∴∠EBC=2∠CBA,∠ACF=2∠FCD,∵AB∥CD,∴∠CBA=∠FCD,
∴∠EBC=∠ACF,∴AC∥BE
(2)∠E与∠FCD互余,理由为:∵AC∥BE,∴∠E=∠ACE,
∵CD平分∠ACF,∴∠ACD=∠FCD,∵DC⊥EC,∴∠ACE+∠ACD=90°,
∴∠E+∠FCD=90°,即∠E与∠FCD互余
