第二十七章相似 作业设计(表格式)2023—2024学年人教版数学九年级下册
文档属性
| 名称 | 第二十七章相似 作业设计(表格式)2023—2024学年人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 796.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览


文档简介
作业设计
作业设计团队所在学校(签章):
作业涉及教科书版本: 人教版 年级及册次:九年级下册
作业涉及单元、章节(或主题、任务):第二十七章 相似
作业设计团队教师姓名(不超过 5 个):
本单元是人教版初中数学第二十七章《相似》。本单元包括图形的相似、相似三角形和位似三节的内容。位似是具有特殊位置关系的相似,是学生在已经掌握相似的相关知识的基础上进行探究。这一节需要设计两个课时的作业,第一课时主要是位似的概念、性质和作图,第二课时主要是平面直角坐标系中的相似。通过这一节作业的练习,让学生进一步体会位似的实际应用价值。通过测量旗杆高度这一综合实践作业,综合考查了学生利用所学的知识去创造性地解决生活中的真实问题的能力,在动手过程中,领悟其中的数学原理并感受学科价值,进而 提高学生学习数学的兴趣,培养用数学方法解决实际问题的能力。
作业一 第 1 课时(位似)
使用时段 作业内容 作业设计 设计意图 使用者 预计时长 预估难度系 数
课前 基础性作业 1、请完善本课的知识结构图: 2、下列图形中,不是位似图形的是( ) A、 B、 1、通 过填空的形式将新课必备的知识以结构化的方式进 行 复习,为课堂上学习位似图形的概念、性质和画法奠定基础。 2、用 选择题的形式考查学生对位似图形概念的理解。 全体学生 5 分钟 0.9
C、 D、
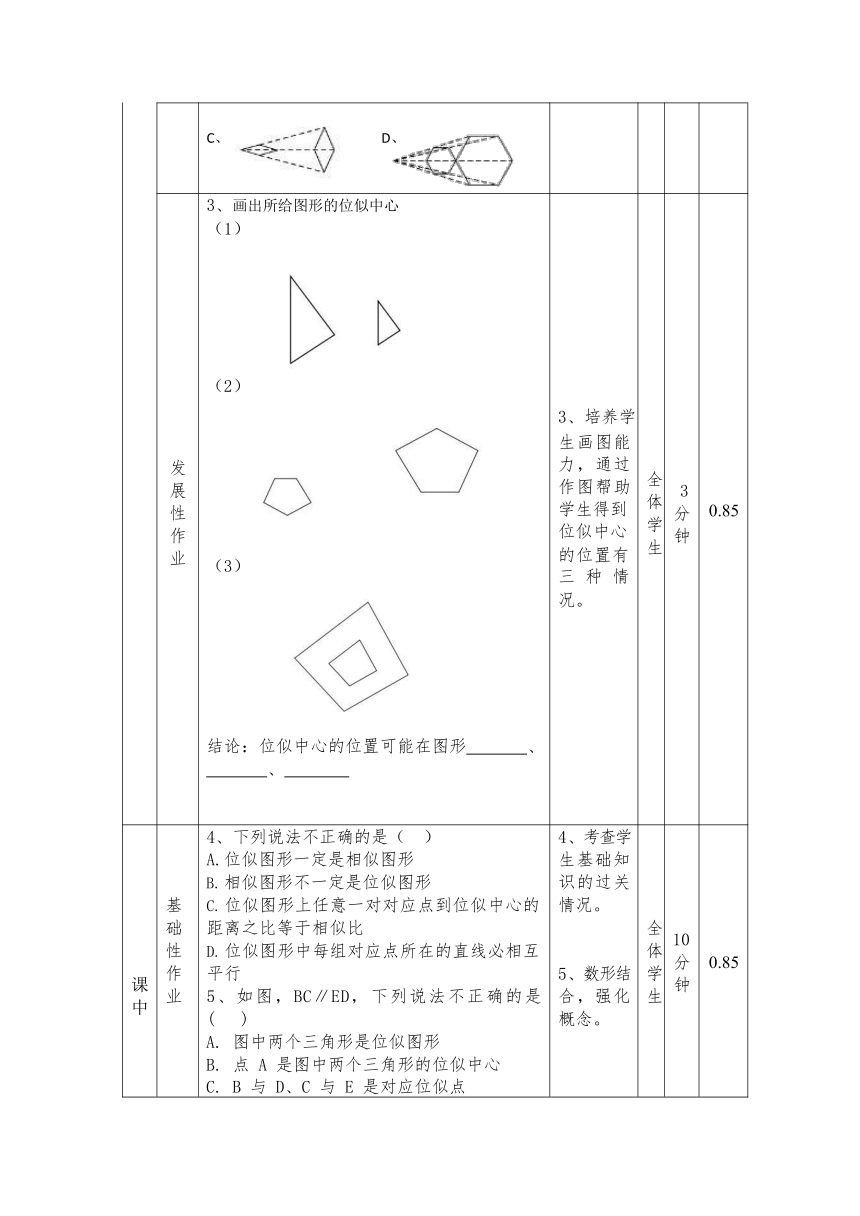
发展性作业 3、画出所给图形的位似中心 全体学生 3 分钟
(1)
(2)
3、培养学
生画图能力,通过作图帮助学生得到 0.85
位似中心
(3) 的位置有 三 种 情
况。
结论:位似中心的位置可能在图形 、 、
课中 基础性作业 4、下列说法不正确的是( ) A.位似图形一定是相似图形 相似图形不一定是位似图形 位似图形上任意一对对应点到位似中心的距离之比等于相似比 位似图形中每组对应点所在的直线必相互平行 5 、如图, BC∥ED, 下列说法不正确的是( ) 图中两个三角形是位似图形 点 A 是图中两个三角形的位似中心 B 与 D、C 与 E 是对应位似点 4、考查学生基础知识的过关情况。 5、数形结合,强化概念。 全体学生 10 分钟 0.85
D. AE∶AD 等于相似比
6、如图, △ABC 与△DEF 是位似图形, 相似比为 2∶3, 已知 AB=4, 则 DE 的长等于( ) A.6 B.5 C.9 D. 8 3 6、巩固位似图形对应线段的数量关系
7、如图,四边形木框 ABCD 在灯泡 O 发出的光 照 射 下 形 成 的 影 子 是 四 边 形A′B′C′D′,若 OB : O′B′=1 : 2,则四边形 ABCD 的面积与四边形 A′B′C′D′ 的面积比为( ) A.4∶1 7、体 会投影是用了位似原理。
B. 2 ∶1
C.1∶ 2
D.1∶4 8、如图,△ABC,根据要求作△A'B'C',使 △A' B' C'∽△ABC,且相似比为 1 : 5. 以点 O 为位似中心; 以点 C 为位似中心. 8、培养学生动手作图能力。
发展性作业 9、物理课后小明自制了一个小孔成像装置, 其中纸筒的长度为 15cm,他准备了一支长为20cm 的蜡烛,想要得到高度为 5cm 的像,蜡烛应放在距离纸筒多远的地方?并说明理由。 9、加强学科联系, 利用位似知识解决物理学科中的小孔成 像 问题。 全体学生 3 分钟 0.85
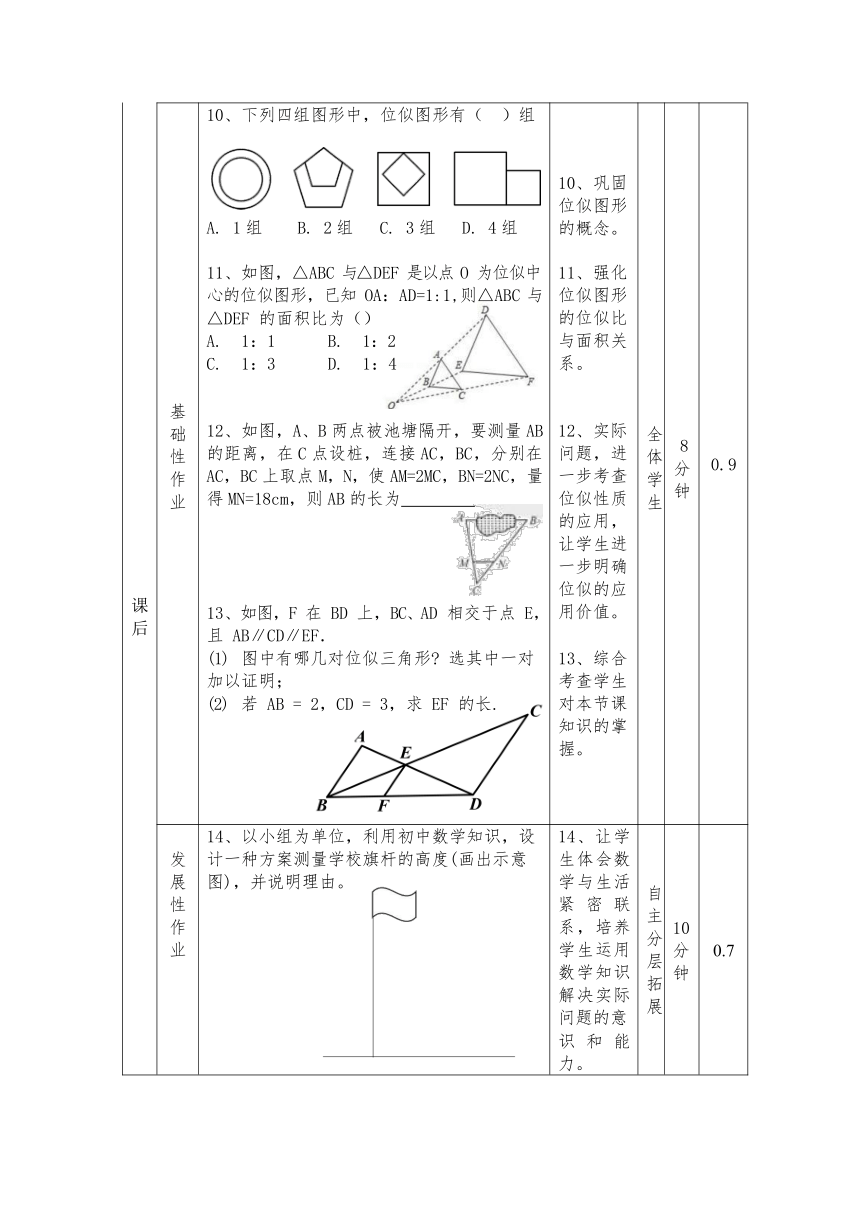
课后 基础性作业 10、下列四组图形中,位似图形有( )组 全体学生 8 分钟
A. 1 组 B. 2 组 C. 3 组 D. 4 组 10、巩固位似图形的概念。
11、如图,△ABC 与△DEF 是以点 O 为位似中心的位似图形,已知 OA:AD=1:1,则△ABC 与 △DEF 的面积比为() A. 1:1 B. 1:2 C. 1:3 D. 1:4 11、强化位似图形的位似比与面积关系。
12、如图,A、B 两点被池塘隔开,要测量 AB 的距离,在 C 点设桩,连接 AC,BC,分别在AC,BC 上取点 M,N,使 AM=2MC,BN=2NC,量得 MN=18cm,则 AB 的长为 13、如图,F 在 BD 上,BC、AD 相交于点 E, 且 AB∥CD∥EF. 图中有哪几对位似三角形 选其中一对加以证明; 若 AB = 2,CD = 3,求 EF 的长. 12、实际问题,进一步考查位似性质的应用, 让学生进一步明确位似的应用价值。 13、综合考查学生对本节课知识的掌握。 0.9
发展性作业 14、以小组为单位,利用初中数学知识,设计一种方案测量学校旗杆的高度(画出示意图),并说明理由。 14、让学生体会数学与生活紧 密 联系,培养学生运用数学知识解决实际问题的意 识 和 能力。 自主分层拓展 10 分钟 0.7
作业涉及教科书版本: 人教版 年级及册次:九年级下册
作业涉及单元、章节(或主题、任务):第二十七章 相似 27.3 位似(2)
作业设计团队教师姓名(不超过 5 个):周文燕、代雨、陈强、雷星成
本单元是人教版初中数学第二十七章《相似》。在上一课时学习了位似图形及相关概念后,学生动手将一些简单图形进行了放大或缩小,会利用橡皮筋等方法做近似的放大图形,己获得一些相关的知识经验和体验,这些知识的储备为本节课的学习奠定了基础。本节课将多边形放到直角坐标系中,探讨通过直角坐标系,如何寻找它关于原点 o 的位似图形并确定相似比,如何将一个多边形放大或缩小。同时,也要探讨在直角坐标系中,给出相似比,如何确定一个己知多边形关于原点 o 的位似图形。通过具有挑战性的内容,促使学生进一步理解位似的相关概念,熟练掌握利用直角坐标系将一个图形按比例放大或缩小,进而能初步归纳出规律,形成有关技能,发展思维能力。本节课将观察、动手操作等实践活动 贯穿于教学活动的始终。同时,有意识地培养学生积极的情感和态度。
作业一 第 2 课时(位似)
使用时段 作业内容 作业设计 设计意图 使用者 预计时长 预估难度系 数
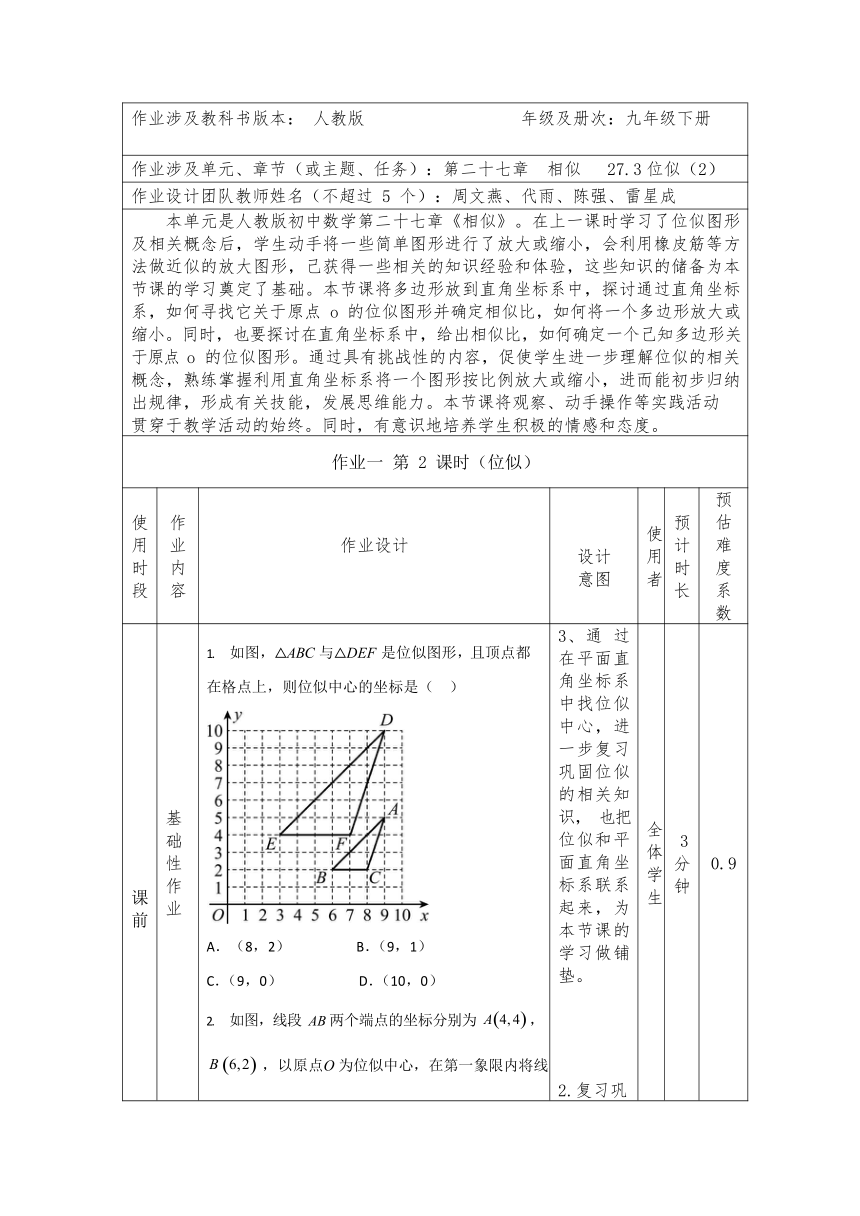
课前 基础性作业 如图,△ABC 与△DEF 是位似图形,且顶点都在格点上,则位似中心的坐标是( ) A.(8,2) B.(9,1) C.(9,0) D.(10,0) 如图,线段 AB 两个端点的坐标分别为 A4, 4 , B 6, 2 ,以原点O 为位似中心,在第一象限内将线 3、通 过在平面直角坐标系中找位似中心,进一步复习巩固位似的相关知识, 也把位似和平面直角坐标系联系起来,为本节课的学习做铺垫。 2.复习巩 全体学生 3 分钟 0.9
段 AB 缩小为原来的 1 后得到线段CD ,则端点 D 的 2 固位似的 相 关 知
坐标为( ) 识,培养
学生通过 添加辅助线构造相似来解决问题的能力。
A. 2, 2 B. 2,1
C. 3, 2 D. 3,1
发展性作业 3.如图,在平面直角坐标系中,△ABC 的三个顶点 全体学生 5 分钟
的坐标分别为点 A(1,0) B(3,0)、C(0,1).
3、培养学生画图能力,通过作图帮助学生得到位似后的 0.85
(1)①以点 M(2,2)为位似中心,在网格区域内画 图形。
出 DEF ,使得 DEF 与 ABC 位似,且点 D 与点
A 对应,位似比为 2:1;
②点 D 坐标为 ;
(2) DEF 的面积为 个平方单位.
课中 基础性作业 4.如图,在平面直角坐标系中, ABC 与 ABC 位似,位似中心为原点 O,已知点 A(1, 1) ,C(4, 1) , AC 6 ,则点C 的坐标为( ) 4、考查学生位似与坐标结合的基础知识的过关情况。 全体学生 15 分钟 0.85
A. (2, 2) B. (4, 2) B. (6, 2) D. (8, 2) 如图,已知矩形OABC 与矩形ODEF 是位似图形, P 是位似中心,若点 B 的坐标为2, 4 ,点 E 的坐标为(-1, 2),则点 P 的坐标为 . 在平面直角坐标系中,把 ABC 以原点为位似中心缩小得到 ABC .若点A 和对应点 A 的坐标分别为(2, 6) 和(1, 3) ,则 ABC 与 ABC 的周长比为 ( ) 1 A.2 B. 2 1 C. 3 D.3 7.如图,在平面直角坐标系中, OAB 和 OCD 是以原点 O 为位似中心的位似图形,已知 B( 4,0), D(2,0),则 OAB 与 OCD 的面积比为( ) 5、巩固利
用位似求
坐标的运
用。
6、巩 固
位似比与
周长比的
关系。
7、利用坐
标求线段
长,强化
位似与面
积 的 关
系。
A.1∶2 B.1∶4
C.2∶1 D.4∶1
8.如图, ABC 中,A、B 两个顶点在 x 轴的上方, 点 C 的坐标是1, 0 ,以点 C 为位似中心,在 x 轴的 下方作 ABC 的位似图形△ABC ,使△ABC 与 8、数形结合,用字母代替数字。
ABC 的位似比为2 :1,设点 B 的横坐标是 a,则点
B 的对应点 B的横坐标是( )
A. 2a 2 B. 2 a 1
C. 2a 2 D. 2a 3
发展性作业 9.如图,在平面直角坐标系中, ABC 三个顶点分别为 A 1, 2 , B 3,1 , C 2, 3 . 9、巩固作图技巧, 体会分类思想,总结作位似图 的 规 律。 全体学生 5 分钟 0.8
以坐标原点O 为位似中心,位似比为 2,将 ABC 放大得到 ABC ,请在平面直角坐标系中画出 ABC ; 设 ABC 与 ABC 的周长分别为C 和C ,求 C1 1 2 C 2 的值.
课后 基础性作业 10.如图,在平面点角坐标系中 AOB 与 COD 是 11、巩固位似图形的位似比与坐标的关系。 11、强化位似图形的位似比与坐标的关系。 全体学生
位似图形,以原点 O 为位似中心,若 AC 2OA ,B
点坐标为(4,2),则点 D 的坐标为( )
15 分钟 0.9
A.( 8,4) B.(8,6)
C.(12,4) D.(12,6)
11.如图,在平面直角坐标系中, ABC 与 ABC
位似,位似中心为原点 O,位似比为 1:2,若点
C 4, 6 ,则点C 的坐标为( )
A. 8, 12 B. 12, 8
C. 6, 12 D. 12, 6
12.在如图所示的正方形网格图中,已知点 12、强化
A 4, 4,B 5, 2 ,若以点 D 为位似中心,把 ABC 位似图形 的位似比
与坐标的
放大到原来的 2 倍,则点A 的对应点的坐标为( ) 关系。
A. 0, 0 B.(2, -1)
C. 2, 2 D. 2, 2
13.以原点O 为位似中心,作 ABC 的位似图形 13、考察学生分析
ABC , ABC 与 ABC的位似比为 1 ,若点C 3 问题的能 力和分类
的坐标为4,1 ,则点C 的坐标为( ) 思想的运
A. 12, 3 用。
B. 12, 3 或12, 3
C. 12, 3
D. 12, 3 或 12, 3
如图,在 ABC 中,点A 的坐标为3, 6 ,以原点O 为位似中心,将 ABC 位似缩小后得到 ABC .若点 A 的坐标为1, 2 , ABC 的面积为 1,则 ABC 的面积为 在平面直角坐标系 xOy 中,以原点O 为位似中心,把 ABO 缩小为原来的 1 ,得到 CDO ,则点 2 A(4, 2) 的对应点C 的坐标是 14、利用
坐标求线
段长,强
化位似与
面积的关
系。
15、考察
学生分析
问题的能
力和分类
思想的运
用。
发展性作业 16.已知在平面直角坐标系中的位置如图所示: 自主分层拓展 8 分钟
(1)在图中画出 ABC 沿 x 轴翻折后的△A1B1C1 ; 16、让学生动手操作画出翻折图形和位 似 图形,并把位似变换与翻折变换 相 结合,让学生体会到 0.7
(2)以点 M (1, 2) 为位似中心,作出△A1B1C1 按2 :1放 数学知识 间是紧密
大后的位似图形△A2 B2C2 ; 联系的。
(3)点 A2 的坐标 ; ABC 与△A2 B2C2 的周
长比是 , ABC 与△A2 B2C2 的面积比是
.
参考答案: 第 1 课时课前
1、略
2、C
3、图形内部、图形外部、图形上课中
4、D
5、D
6、A
7、D
8、略
9、C 课后10、D
11、54
12、
△DFE 与 △DBA,△BFE 与 △BDC,△AEB 与 △DEC 都是位似三角形;证明略.
(2)
∵ AB∥CD∥EF,
∴△BFE∽△BDC,△AEB∽△DEC. 又∵AB = 2,CD = 3,
∴ = = 2
3
∴ = = 2
5
∴ = 6
5
第 2 课时课前
13、C
14、D
3、(1)①图见解析,②点 D 的坐标是(4,6)
(2)4
【分析】(1)①根据位似图形的性质画图即可;②由位似图形的性质即可求得点 D 坐标;
利用(1)中①题的图形,根据三角形的面积公式求解即可.
【详解】(1)解:① DEF 如图所示,
②点 D 的坐标是(4,6);
(2) DEF 的面积= 1 DE 2 1 4 2 4 个平方单位.
2 2
课中
4、D
5、2,0
【详解】解:∵点 B 的坐标为2, 4 ,点 E 的坐标为(-1, 2),
∴ AB 4,OA 2,OD 2 ,
∵矩形OABC 与矩形ODEF 是位似图形,P 是位似中心,
∴ PO OD 2 1 ,
PA AB 4 2
∴ PO OA 2 ,
∴ P 点坐标为2,0 ,故答案为: 2,0 .
7、A
【详解】解:把 ABC 以原点为位似中心缩小得到 ABC,点A 和对应点 A 的坐标分别为
(2, 6) 和(1, 3) ,
则 ABC 与 ABC 的相似比为 2 6 2 ,
1 3
故选:A.
8、D
【详解】解:设 B的横坐标为 x,
则 B、C 间的水平距离为a 1, B、C 间的水平距离为x 1,
∵△ABC 与 ABC 的位似比为2 :1,
∴ 2a 1 x 1 , 解得: x 2a 3 , 故选:D.
9、(1)见解析
1
(2) 2
【详解】(1)解:如图, ABC即为所求的三角形;
(2)解:由(1)可得, △ABC ∽△ABC ,且相似比为1: 2
∴ C1 1
C2 2
课后
10、D
【详解】解:∵ AC 2OA ,
∴ OA 1 ,
OC 3
∴ AOB 与 COD
的位似比为 1 ,
3
∵B 点坐标为(4,2), AOB 与 COD 是以坐标原点 O 为位似中心,
∴点 D 的坐标(4×3,2×3),即(12,6),故选:D.
12、A
【详解】∵点C 4, 6 , C 与 C 关于原点对称,且位似比为1: 2 ,
∴ C 的坐标为4 2 , 2 6
即C8, 12
故选:A.
13、C
【详解】解:∵ A 4, 4, B 5, 2 ,
∴平面直角坐标系如图所示,以点 D 为位似中心,把 ABC 放大到原来的 2 倍,点 A 的对应点为 A ,
则点 A 的坐标为2, 2 , 故选:C.
14、D
【详解】解:在同一象限内,∵ ABC 与 ABC是以原点 O 为位似中心的位似图形,其中
相似比是 1
3
,点C 的坐标为4,1 ,
∴则点C 的坐标为: 12,3 ;
不在同一象限内,∵ ABC 与 ABC 是以原点 O
点C 的坐标为4,1 ,
∴则点C 的坐标为: 12, 3 ,
为位似中心的位似图形,其中相似比是 1 ,
3
故选:D.
14、9
【详解】解∶∵△ABC 和△A'B' C'是以坐标原点 O 为位似中心的位似图形,且点 A (3,6) ,
A'( 1,2),
∴△ABC 与△A'B' C'的相似比等于 3∶ 1.
△△A'B'C'与△ABC 的面积之比为 9 ∶ 1.
∵△A'B'C'的面积为 1,
∴△ABC 的面积为 9. 故选∶ 9.
15、(2,1) 或(2, 1)
【详解】解:根据题意得,位似比是 1 ,且位似比是 1 的三角形有两个, A(4, 2) ,
2 2
∴① A 乘以 1 得, (2,1) ;② A 乘以 1 得, (2, 1) ,
2 2
故选: (2,1) 或(2, 1) .
16、(1)见解析(2)见解析
(3) 3,6 ;1: 2 ;1: 4
【详解】(1)解:如图,△A1B1C1 为所作;
(2)解:如图, △A2 B2C2 为所作;
(3)解:点 A2 的坐标为3,6 ,
∵ ABC 沿 x 轴翻折后的△A1B1C1 ,
∴△ABC ≌△A1B1C1 ,
∵△A1B1C1 按2 :1放大后的位似图形△A2 B2C2 ,
∴△A1B1C1 与△A2 B2C2 的相似比为1: 2 ,
∴ ABC 与△A2 B2C2 的相似比为1: 2 ,
∴ ABC 与△A2 B2C2 的周长的比为1: 2 , ABC 与△A2 B2C2 的面积的比为1: 4 . 故答案为: 3,6 ;1: 2 ;1: 4
作业设计团队所在学校(签章):
作业涉及教科书版本: 人教版 年级及册次:九年级下册
作业涉及单元、章节(或主题、任务):第二十七章 相似
作业设计团队教师姓名(不超过 5 个):
本单元是人教版初中数学第二十七章《相似》。本单元包括图形的相似、相似三角形和位似三节的内容。位似是具有特殊位置关系的相似,是学生在已经掌握相似的相关知识的基础上进行探究。这一节需要设计两个课时的作业,第一课时主要是位似的概念、性质和作图,第二课时主要是平面直角坐标系中的相似。通过这一节作业的练习,让学生进一步体会位似的实际应用价值。通过测量旗杆高度这一综合实践作业,综合考查了学生利用所学的知识去创造性地解决生活中的真实问题的能力,在动手过程中,领悟其中的数学原理并感受学科价值,进而 提高学生学习数学的兴趣,培养用数学方法解决实际问题的能力。
作业一 第 1 课时(位似)
使用时段 作业内容 作业设计 设计意图 使用者 预计时长 预估难度系 数
课前 基础性作业 1、请完善本课的知识结构图: 2、下列图形中,不是位似图形的是( ) A、 B、 1、通 过填空的形式将新课必备的知识以结构化的方式进 行 复习,为课堂上学习位似图形的概念、性质和画法奠定基础。 2、用 选择题的形式考查学生对位似图形概念的理解。 全体学生 5 分钟 0.9
C、 D、
发展性作业 3、画出所给图形的位似中心 全体学生 3 分钟
(1)
(2)
3、培养学
生画图能力,通过作图帮助学生得到 0.85
位似中心
(3) 的位置有 三 种 情
况。
结论:位似中心的位置可能在图形 、 、
课中 基础性作业 4、下列说法不正确的是( ) A.位似图形一定是相似图形 相似图形不一定是位似图形 位似图形上任意一对对应点到位似中心的距离之比等于相似比 位似图形中每组对应点所在的直线必相互平行 5 、如图, BC∥ED, 下列说法不正确的是( ) 图中两个三角形是位似图形 点 A 是图中两个三角形的位似中心 B 与 D、C 与 E 是对应位似点 4、考查学生基础知识的过关情况。 5、数形结合,强化概念。 全体学生 10 分钟 0.85
D. AE∶AD 等于相似比
6、如图, △ABC 与△DEF 是位似图形, 相似比为 2∶3, 已知 AB=4, 则 DE 的长等于( ) A.6 B.5 C.9 D. 8 3 6、巩固位似图形对应线段的数量关系
7、如图,四边形木框 ABCD 在灯泡 O 发出的光 照 射 下 形 成 的 影 子 是 四 边 形A′B′C′D′,若 OB : O′B′=1 : 2,则四边形 ABCD 的面积与四边形 A′B′C′D′ 的面积比为( ) A.4∶1 7、体 会投影是用了位似原理。
B. 2 ∶1
C.1∶ 2
D.1∶4 8、如图,△ABC,根据要求作△A'B'C',使 △A' B' C'∽△ABC,且相似比为 1 : 5. 以点 O 为位似中心; 以点 C 为位似中心. 8、培养学生动手作图能力。
发展性作业 9、物理课后小明自制了一个小孔成像装置, 其中纸筒的长度为 15cm,他准备了一支长为20cm 的蜡烛,想要得到高度为 5cm 的像,蜡烛应放在距离纸筒多远的地方?并说明理由。 9、加强学科联系, 利用位似知识解决物理学科中的小孔成 像 问题。 全体学生 3 分钟 0.85
课后 基础性作业 10、下列四组图形中,位似图形有( )组 全体学生 8 分钟
A. 1 组 B. 2 组 C. 3 组 D. 4 组 10、巩固位似图形的概念。
11、如图,△ABC 与△DEF 是以点 O 为位似中心的位似图形,已知 OA:AD=1:1,则△ABC 与 △DEF 的面积比为() A. 1:1 B. 1:2 C. 1:3 D. 1:4 11、强化位似图形的位似比与面积关系。
12、如图,A、B 两点被池塘隔开,要测量 AB 的距离,在 C 点设桩,连接 AC,BC,分别在AC,BC 上取点 M,N,使 AM=2MC,BN=2NC,量得 MN=18cm,则 AB 的长为 13、如图,F 在 BD 上,BC、AD 相交于点 E, 且 AB∥CD∥EF. 图中有哪几对位似三角形 选其中一对加以证明; 若 AB = 2,CD = 3,求 EF 的长. 12、实际问题,进一步考查位似性质的应用, 让学生进一步明确位似的应用价值。 13、综合考查学生对本节课知识的掌握。 0.9
发展性作业 14、以小组为单位,利用初中数学知识,设计一种方案测量学校旗杆的高度(画出示意图),并说明理由。 14、让学生体会数学与生活紧 密 联系,培养学生运用数学知识解决实际问题的意 识 和 能力。 自主分层拓展 10 分钟 0.7
作业涉及教科书版本: 人教版 年级及册次:九年级下册
作业涉及单元、章节(或主题、任务):第二十七章 相似 27.3 位似(2)
作业设计团队教师姓名(不超过 5 个):周文燕、代雨、陈强、雷星成
本单元是人教版初中数学第二十七章《相似》。在上一课时学习了位似图形及相关概念后,学生动手将一些简单图形进行了放大或缩小,会利用橡皮筋等方法做近似的放大图形,己获得一些相关的知识经验和体验,这些知识的储备为本节课的学习奠定了基础。本节课将多边形放到直角坐标系中,探讨通过直角坐标系,如何寻找它关于原点 o 的位似图形并确定相似比,如何将一个多边形放大或缩小。同时,也要探讨在直角坐标系中,给出相似比,如何确定一个己知多边形关于原点 o 的位似图形。通过具有挑战性的内容,促使学生进一步理解位似的相关概念,熟练掌握利用直角坐标系将一个图形按比例放大或缩小,进而能初步归纳出规律,形成有关技能,发展思维能力。本节课将观察、动手操作等实践活动 贯穿于教学活动的始终。同时,有意识地培养学生积极的情感和态度。
作业一 第 2 课时(位似)
使用时段 作业内容 作业设计 设计意图 使用者 预计时长 预估难度系 数
课前 基础性作业 如图,△ABC 与△DEF 是位似图形,且顶点都在格点上,则位似中心的坐标是( ) A.(8,2) B.(9,1) C.(9,0) D.(10,0) 如图,线段 AB 两个端点的坐标分别为 A4, 4 , B 6, 2 ,以原点O 为位似中心,在第一象限内将线 3、通 过在平面直角坐标系中找位似中心,进一步复习巩固位似的相关知识, 也把位似和平面直角坐标系联系起来,为本节课的学习做铺垫。 2.复习巩 全体学生 3 分钟 0.9
段 AB 缩小为原来的 1 后得到线段CD ,则端点 D 的 2 固位似的 相 关 知
坐标为( ) 识,培养
学生通过 添加辅助线构造相似来解决问题的能力。
A. 2, 2 B. 2,1
C. 3, 2 D. 3,1
发展性作业 3.如图,在平面直角坐标系中,△ABC 的三个顶点 全体学生 5 分钟
的坐标分别为点 A(1,0) B(3,0)、C(0,1).
3、培养学生画图能力,通过作图帮助学生得到位似后的 0.85
(1)①以点 M(2,2)为位似中心,在网格区域内画 图形。
出 DEF ,使得 DEF 与 ABC 位似,且点 D 与点
A 对应,位似比为 2:1;
②点 D 坐标为 ;
(2) DEF 的面积为 个平方单位.
课中 基础性作业 4.如图,在平面直角坐标系中, ABC 与 ABC 位似,位似中心为原点 O,已知点 A(1, 1) ,C(4, 1) , AC 6 ,则点C 的坐标为( ) 4、考查学生位似与坐标结合的基础知识的过关情况。 全体学生 15 分钟 0.85
A. (2, 2) B. (4, 2) B. (6, 2) D. (8, 2) 如图,已知矩形OABC 与矩形ODEF 是位似图形, P 是位似中心,若点 B 的坐标为2, 4 ,点 E 的坐标为(-1, 2),则点 P 的坐标为 . 在平面直角坐标系中,把 ABC 以原点为位似中心缩小得到 ABC .若点A 和对应点 A 的坐标分别为(2, 6) 和(1, 3) ,则 ABC 与 ABC 的周长比为 ( ) 1 A.2 B. 2 1 C. 3 D.3 7.如图,在平面直角坐标系中, OAB 和 OCD 是以原点 O 为位似中心的位似图形,已知 B( 4,0), D(2,0),则 OAB 与 OCD 的面积比为( ) 5、巩固利
用位似求
坐标的运
用。
6、巩 固
位似比与
周长比的
关系。
7、利用坐
标求线段
长,强化
位似与面
积 的 关
系。
A.1∶2 B.1∶4
C.2∶1 D.4∶1
8.如图, ABC 中,A、B 两个顶点在 x 轴的上方, 点 C 的坐标是1, 0 ,以点 C 为位似中心,在 x 轴的 下方作 ABC 的位似图形△ABC ,使△ABC 与 8、数形结合,用字母代替数字。
ABC 的位似比为2 :1,设点 B 的横坐标是 a,则点
B 的对应点 B的横坐标是( )
A. 2a 2 B. 2 a 1
C. 2a 2 D. 2a 3
发展性作业 9.如图,在平面直角坐标系中, ABC 三个顶点分别为 A 1, 2 , B 3,1 , C 2, 3 . 9、巩固作图技巧, 体会分类思想,总结作位似图 的 规 律。 全体学生 5 分钟 0.8
以坐标原点O 为位似中心,位似比为 2,将 ABC 放大得到 ABC ,请在平面直角坐标系中画出 ABC ; 设 ABC 与 ABC 的周长分别为C 和C ,求 C1 1 2 C 2 的值.
课后 基础性作业 10.如图,在平面点角坐标系中 AOB 与 COD 是 11、巩固位似图形的位似比与坐标的关系。 11、强化位似图形的位似比与坐标的关系。 全体学生
位似图形,以原点 O 为位似中心,若 AC 2OA ,B
点坐标为(4,2),则点 D 的坐标为( )
15 分钟 0.9
A.( 8,4) B.(8,6)
C.(12,4) D.(12,6)
11.如图,在平面直角坐标系中, ABC 与 ABC
位似,位似中心为原点 O,位似比为 1:2,若点
C 4, 6 ,则点C 的坐标为( )
A. 8, 12 B. 12, 8
C. 6, 12 D. 12, 6
12.在如图所示的正方形网格图中,已知点 12、强化
A 4, 4,B 5, 2 ,若以点 D 为位似中心,把 ABC 位似图形 的位似比
与坐标的
放大到原来的 2 倍,则点A 的对应点的坐标为( ) 关系。
A. 0, 0 B.(2, -1)
C. 2, 2 D. 2, 2
13.以原点O 为位似中心,作 ABC 的位似图形 13、考察学生分析
ABC , ABC 与 ABC的位似比为 1 ,若点C 3 问题的能 力和分类
的坐标为4,1 ,则点C 的坐标为( ) 思想的运
A. 12, 3 用。
B. 12, 3 或12, 3
C. 12, 3
D. 12, 3 或 12, 3
如图,在 ABC 中,点A 的坐标为3, 6 ,以原点O 为位似中心,将 ABC 位似缩小后得到 ABC .若点 A 的坐标为1, 2 , ABC 的面积为 1,则 ABC 的面积为 在平面直角坐标系 xOy 中,以原点O 为位似中心,把 ABO 缩小为原来的 1 ,得到 CDO ,则点 2 A(4, 2) 的对应点C 的坐标是 14、利用
坐标求线
段长,强
化位似与
面积的关
系。
15、考察
学生分析
问题的能
力和分类
思想的运
用。
发展性作业 16.已知在平面直角坐标系中的位置如图所示: 自主分层拓展 8 分钟
(1)在图中画出 ABC 沿 x 轴翻折后的△A1B1C1 ; 16、让学生动手操作画出翻折图形和位 似 图形,并把位似变换与翻折变换 相 结合,让学生体会到 0.7
(2)以点 M (1, 2) 为位似中心,作出△A1B1C1 按2 :1放 数学知识 间是紧密
大后的位似图形△A2 B2C2 ; 联系的。
(3)点 A2 的坐标 ; ABC 与△A2 B2C2 的周
长比是 , ABC 与△A2 B2C2 的面积比是
.
参考答案: 第 1 课时课前
1、略
2、C
3、图形内部、图形外部、图形上课中
4、D
5、D
6、A
7、D
8、略
9、C 课后10、D
11、54
12、
△DFE 与 △DBA,△BFE 与 △BDC,△AEB 与 △DEC 都是位似三角形;证明略.
(2)
∵ AB∥CD∥EF,
∴△BFE∽△BDC,△AEB∽△DEC. 又∵AB = 2,CD = 3,
∴ = = 2
3
∴ = = 2
5
∴ = 6
5
第 2 课时课前
13、C
14、D
3、(1)①图见解析,②点 D 的坐标是(4,6)
(2)4
【分析】(1)①根据位似图形的性质画图即可;②由位似图形的性质即可求得点 D 坐标;
利用(1)中①题的图形,根据三角形的面积公式求解即可.
【详解】(1)解:① DEF 如图所示,
②点 D 的坐标是(4,6);
(2) DEF 的面积= 1 DE 2 1 4 2 4 个平方单位.
2 2
课中
4、D
5、2,0
【详解】解:∵点 B 的坐标为2, 4 ,点 E 的坐标为(-1, 2),
∴ AB 4,OA 2,OD 2 ,
∵矩形OABC 与矩形ODEF 是位似图形,P 是位似中心,
∴ PO OD 2 1 ,
PA AB 4 2
∴ PO OA 2 ,
∴ P 点坐标为2,0 ,故答案为: 2,0 .
7、A
【详解】解:把 ABC 以原点为位似中心缩小得到 ABC,点A 和对应点 A 的坐标分别为
(2, 6) 和(1, 3) ,
则 ABC 与 ABC 的相似比为 2 6 2 ,
1 3
故选:A.
8、D
【详解】解:设 B的横坐标为 x,
则 B、C 间的水平距离为a 1, B、C 间的水平距离为x 1,
∵△ABC 与 ABC 的位似比为2 :1,
∴ 2a 1 x 1 , 解得: x 2a 3 , 故选:D.
9、(1)见解析
1
(2) 2
【详解】(1)解:如图, ABC即为所求的三角形;
(2)解:由(1)可得, △ABC ∽△ABC ,且相似比为1: 2
∴ C1 1
C2 2
课后
10、D
【详解】解:∵ AC 2OA ,
∴ OA 1 ,
OC 3
∴ AOB 与 COD
的位似比为 1 ,
3
∵B 点坐标为(4,2), AOB 与 COD 是以坐标原点 O 为位似中心,
∴点 D 的坐标(4×3,2×3),即(12,6),故选:D.
12、A
【详解】∵点C 4, 6 , C 与 C 关于原点对称,且位似比为1: 2 ,
∴ C 的坐标为4 2 , 2 6
即C8, 12
故选:A.
13、C
【详解】解:∵ A 4, 4, B 5, 2 ,
∴平面直角坐标系如图所示,以点 D 为位似中心,把 ABC 放大到原来的 2 倍,点 A 的对应点为 A ,
则点 A 的坐标为2, 2 , 故选:C.
14、D
【详解】解:在同一象限内,∵ ABC 与 ABC是以原点 O 为位似中心的位似图形,其中
相似比是 1
3
,点C 的坐标为4,1 ,
∴则点C 的坐标为: 12,3 ;
不在同一象限内,∵ ABC 与 ABC 是以原点 O
点C 的坐标为4,1 ,
∴则点C 的坐标为: 12, 3 ,
为位似中心的位似图形,其中相似比是 1 ,
3
故选:D.
14、9
【详解】解∶∵△ABC 和△A'B' C'是以坐标原点 O 为位似中心的位似图形,且点 A (3,6) ,
A'( 1,2),
∴△ABC 与△A'B' C'的相似比等于 3∶ 1.
△△A'B'C'与△ABC 的面积之比为 9 ∶ 1.
∵△A'B'C'的面积为 1,
∴△ABC 的面积为 9. 故选∶ 9.
15、(2,1) 或(2, 1)
【详解】解:根据题意得,位似比是 1 ,且位似比是 1 的三角形有两个, A(4, 2) ,
2 2
∴① A 乘以 1 得, (2,1) ;② A 乘以 1 得, (2, 1) ,
2 2
故选: (2,1) 或(2, 1) .
16、(1)见解析(2)见解析
(3) 3,6 ;1: 2 ;1: 4
【详解】(1)解:如图,△A1B1C1 为所作;
(2)解:如图, △A2 B2C2 为所作;
(3)解:点 A2 的坐标为3,6 ,
∵ ABC 沿 x 轴翻折后的△A1B1C1 ,
∴△ABC ≌△A1B1C1 ,
∵△A1B1C1 按2 :1放大后的位似图形△A2 B2C2 ,
∴△A1B1C1 与△A2 B2C2 的相似比为1: 2 ,
∴ ABC 与△A2 B2C2 的相似比为1: 2 ,
∴ ABC 与△A2 B2C2 的周长的比为1: 2 , ABC 与△A2 B2C2 的面积的比为1: 4 . 故答案为: 3,6 ;1: 2 ;1: 4
