第6单元圆易错卷(单元测试含答案)2023-2024学年数学五年级下册苏教版
文档属性
| 名称 | 第6单元圆易错卷(单元测试含答案)2023-2024学年数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 562.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 21:41:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元圆易错卷(单元测试)2023-2024学年数学五年级下册苏教版
一、选择题
1.钟面上的时针从“2”走到“5”,扫过部分是一个圆心角为( )的扇形。
A.30° B.90° C.50° D.60°
2.算式3.14×7+7×2求的是半径为7厘米的( )。
A.圆的周长 B.圆的面积
C.半圆的周长 D.半圆的面积
3.有一块面积为72平方分米的长方形钢板,用激光切割出两个圆(如图)。其中一个圆的面积是( )平方分米。
A.6π B.9π C.36 D.36π
4.明明在学习圆的周长时,把一个直径是2厘米的圆形卡片在直尺上滚动一周。下面测量最接近准确值的一次是( )。
A. B.
C. D.
5.如图,空白部分的面积和涂色部分的面积相比,结果是( )。
A.空白部分的面积大 B.涂色部分的面积大
C.两部分的面积相等 D.无法确定
6.下面五句话,正确的有( )句。
(1)任意两个素数的和都是偶数。
(2)真分数都比1小,假分数一定比1大。
(3)两个数的积一定是这两个数的公倍数。
(4)1+2+3+4+…+29的和是奇数
(5)大约1500年前,我国南北朝科学家祖冲之是世界上第一个把圆周率的值精确到小数点后7位的人。
A.1 B.2 C.3 D.4
二、填空题
7.画圆时固定的一点叫作( ),用字母( )表示;连接( )到( )任意一点的线段叫作半径,用字母( )表示;通过圆心并且两端都在( )的线段叫作( ),用字母( )表示。
8.用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是( )厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是( )厘米。
9.如下图,一块圆形铝皮的周长是18.84dm,它的半径是( )dm;从中截取一个最大的正方形,剩下阴影部分的面积是( )dm2。
10.如图,等腰直角三角形的一条腰长4厘米,阴影部分可以拼成一个半径是( )厘米的半圆,空白部分的面积是( )平方厘米。
11.用一张长为10厘米、宽为6厘米的纸剪成一个最大的圆,这个圆的面积是( )平方厘米。
12.如图钟面上显示时针从“2”走到“5”,这段时间分针一共旋转了( )°;如果时针的长度为4厘米,这段时间时针扫过的面积是( )平方厘米。(π取3.14)
三、判断题
13.如果圆和正方形的周长相等,那么圆的直径大于正方形的边长。( )
14.只要给出圆心的位置和半径的具体数值,就能画出一个圆。( )
15.如图:这两个图形中圆的直径都是1cm,那么阴影部分的面积相等。 ( )
16.两个扇形,圆心角大的扇形面积不一定大。 ( )
17.把一张圆形纸片对折后打开,换个方向再对折.两条折痕的交点就是这个圆的圆心.( )
四、计算题
18.求图形中阴影部分的周长和面积。(单位:厘米)
19.求下列图形中涂色部分的面积。(单位:厘米)
五、解答题
20.一棵树树干横截面周长是62.8厘米,一根绳子绕树10圈后还多出72厘米。这根绳子长多少米?
21.滨江公园有一个近似圆形的湖面,它的直径大约400米。
(1)沿湖的一周每隔4米栽一棵柳树,一共要栽多少棵柳树?
(2)在湖里养鱼,按每平方米水面能养6条鱼计算,湖里大约一共能养多少条鱼?
22.学校“六一”庆祝活动要搭一座高2.5米的半圆形气球拱门(如图),现在有一条长8米的气球串,做半圆形拱门够吗?
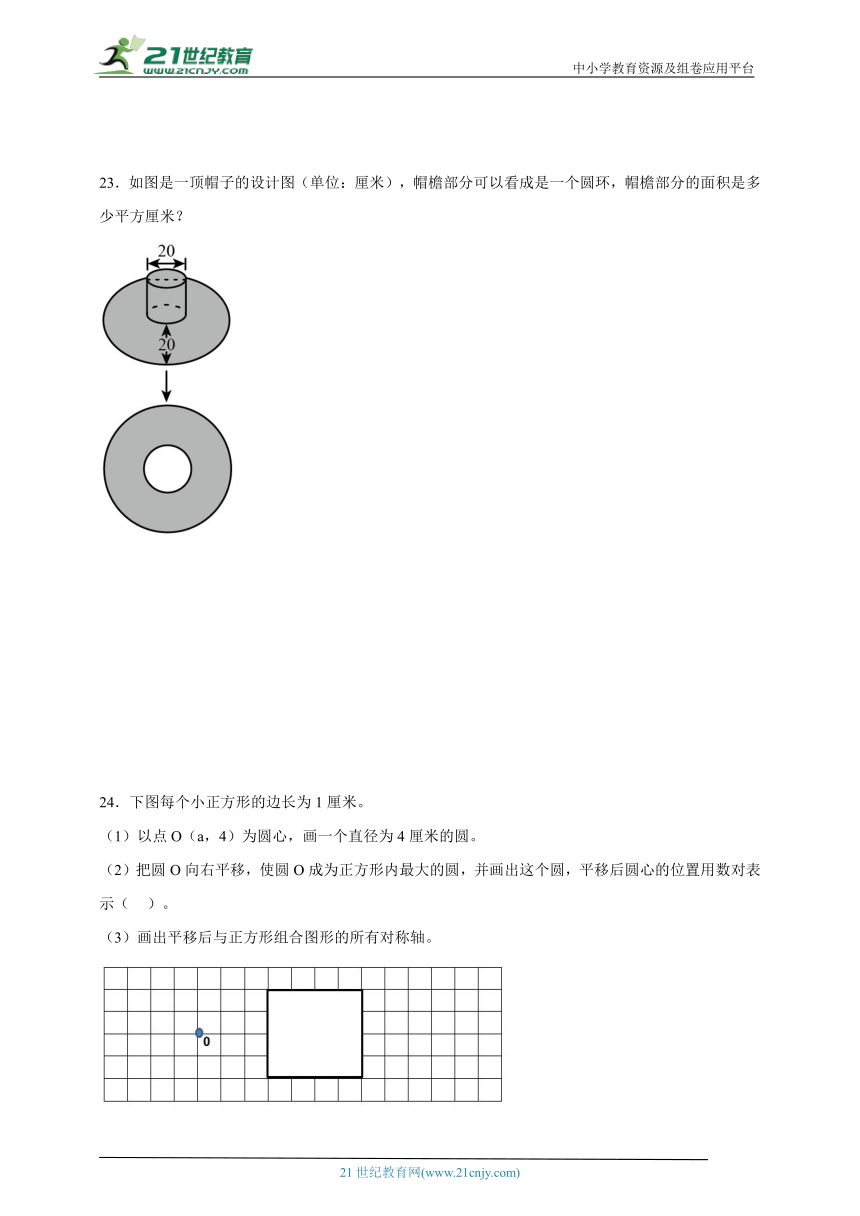
23.如图是一顶帽子的设计图(单位:厘米),帽檐部分可以看成是一个圆环,帽檐部分的面积是多少平方厘米?
24.下图每个小正方形的边长为1厘米。
(1)以点O(a,4)为圆心,画一个直径为4厘米的圆。
(2)把圆O向右平移,使圆O成为正方形内最大的圆,并画出这个圆,平移后圆心的位置用数对表示( )。
(3)画出平移后与正方形组合图形的所有对称轴。
参考答案:
1.B
【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°,据此解答即可。
【详解】钟面上时针从“2”走到“5”,走了3大格,30°×3=90°,即经过的部分是一个圆心角90°的扇形。
故答案为:B
【点睛】关键弄清时针从一个数字走到相邻的另一个数字绕中心旋转了30°。
2.C
【分析】根据半圆周长的意义:半圆的周长等于这个圆周长的一半加上一条直径的长度,据此解答。
【详解】半径为7厘米圆的周长是:3.14×7×2
半径为7厘米的半圆的周长是:
3.14×7×2÷2+7×2
=3.14×7+7×2
算式3.14×7+7×2求的是半径为7厘米的半圆的周长。
故答案为:C
【点睛】熟练掌握半圆的周长的意义、半径周长的计算公式以及应用。
3.B
【分析】根据图可知,长方形的宽是圆的直径,长方形的长是圆直径的2倍,可以设圆的半径为r分米,即长方形的宽:2r分米;长方形的长:4r分米。由于长方形的面积是72平方分米,根据长方形的面积公式:长×宽,即2r×4r=72,由此即可求出r的平方,之后再根据圆的面积公式:S=πr2,把数代入即可求解。
【详解】解:设圆的半径为r分米,长方形的宽:2r分米,长方形的长:4r分米。
2r×4r=72
8r2=72
r2=72÷8
r2=9
圆的面积:9π平方分米。
故答案为:B
【点睛】本题主要考查长方形和圆的面积公式,熟练掌握它们的面积公式并灵活运用。
4.C
【分析】根据圆的周长公式:周长=π×直径;代入数据,求出圆的周长,再进行比较,即可解答。
【详解】3.14×2=6.28(厘米)
A.7.3厘米,不符合题意;
B.5.6厘米,不符合题意;
C.6.3厘米,与6.28接近,符合题意;
D.3.5厘米,不符合题意。
故答案为:C
【点睛】利用圆的周长公式进行解答,关键是熟记公式。
5.C
【分析】设半圆的直径是4厘米,则空白部分圆的直径:4÷2=2厘米;根据圆的面积公式:面积=π×半径2,分别求出半圆的面积和空白圆的面积,进而求出涂色部分的面积,再进行比较,即可解答。
【详解】设半圆直径为4厘米,则空白圆的直径为:4÷2=2(厘米)
半圆面积:3.14×(4÷2)2÷2
=3.14×4÷2
=12.56÷2
=6.28(平方厘米)
空白圆的面积:3.14×(2÷2)2
=3.14×1
=3.14(平方厘米)
涂色部分面积:6.28-3.14=3.14(平方厘米)
3.14=3.14,空白部分面积等于涂色部分面积。
如图,空白部分的面积和涂色部分的面积相比,结果是两部分的面积相等。
故答案为:C
【点睛】熟练掌握圆的面积公式是解答本题的关键。
6.B
【分析】素数也是质数;一个数,除了1和它本身两个因数没有其它因数,这样的数叫做质数,质数+质数=奇数,质数+质数=偶数,第一小题据此判断;
分子小于分母的分数叫做真分数;分子大于或等于分母的分数叫做假分数,第二小题据此判断;
如果整数a能被整数b整除(a≠0,b≠0),a就叫做b的倍数;两个数公有的倍数叫做这两个数的公倍数,第三小题据此判断;
奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数,第四小题据此判断;
祖冲之是世界上第一个把圆周率的值精确度小数点后7位的人,第五小题据此判断。
【详解】(1)素数是质数;如,2+3=5,5是奇数,3+5=8;任意两个素数的和可能是奇数,也可能是偶数,原题干说法错误;
(2)真分数都小于1,假分数大于或等于1,原题干说法错误;
(3)因数和倍数是在整数范畴,两个小数的乘积就不是它们的公倍数,如:0.2×0.1=0.02,我们不能说0.02是0.1和0.2的公倍数,原题干说法错误;
(4)1+2+3+4+…+29,是由15个奇数相加和14个偶数相加;和是奇数,原题干说法正确;
(5)祖冲之是世界上第一个把圆周率的值精确度小数点后7位的人,原题干说法正确。
(4)(5)2句话说法正确。
下面五句话,正确的有2句话。
故答案为:B
【点睛】本题考查的知识点角度,属于基础知识,要熟练掌握。
7. 圆心 O 圆心 圆上 r 圆上 直径 d
【分析】画圆时,固定的点叫圆心,用O表示,圆心到圆上的距离是是半径,半径用r表示,圆的直径是一条经过圆心,两端在圆上的线段,直径用d表示,据此即可填空。
【详解】由分析可知:
画圆时固定的一点叫作圆心,用字母O表示;连接圆心到圆上任意一点的线段叫作半径,用字母r表示;通过圆心并且两端都在圆上的线段叫作直径,用字母d表示。
如下图所示:
【点睛】本题主要考查圆的概念,熟练掌握圆的含义是解题的关键。
8. 5 41.4
【分析】圆规两脚间的距离就是圆的半径,根据半径=直径÷2,据此求出圆规两脚间的距离;把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长比圆的周长多两条半径的长度。据此填空即可。
【详解】10÷2=5(厘米)
3.14×10+10
=31.4+10
=41.4(厘米)
用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是5厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是41.4厘米。
【点睛】本题考查圆的周长,明确圆规两脚间的距离就是圆的半径是解题的关键。
9. 3 10.26
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出半径;阴影部分面积=圆的面积-正方形面积;正方形的对角线等于圆的直径;把正方形分成两个完全相同的三角形,根据圆的面积公式:面积=π×半径2;三角形面积公式:面积=半径×直径÷2,代入数据,即可解答。
【详解】18.84÷3.14÷2
=6÷2
=3(dm)
3.14×32-3×(3×2)÷2×2
=3.14×9-3×6÷2×2
=28.26-18÷2×2
=28.26-9×2
=28.26-18
=10.26(dm2)
【点睛】利用圆的周长公式、面积公式和三角形面积公式进行解答,关键是熟记公式,灵活运用。
10. 2 1.72
【分析】根据图可知,这个是等腰直角三角形,即三个角分别为45°、45°、90°,由于三个阴影部分可以看成一个半径是2厘米的90°的扇形;和2个半径是2厘米的圆心角是45°的扇形,即90°+45°+45°=180°,则阴影部分可以拼成一个半径是2厘米的半圆;根据三角形的面积公式:底×高÷2,半圆的面积公式:S=πr2÷2,把数代入公式即可求解。
【详解】由分析可知:
90°+45°+45°=180°
即阴影部分可以拼成一个半径是2厘米的半圆
2+2=4(厘米)
4×4÷2-3.14×2×2÷2
=8-6.28
=1.72(平方厘米)
【点睛】本题主要考查三角形和半圆的面积公式,熟练掌握它们的面积公式并灵活运用。
11.28.26
【分析】由题意可知,这个最大的圆的直径相当于长方形的宽,然后根据圆的面积公式:S=πr2,据此解答即可。
【详解】3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
【点睛】本题考查圆的面积,明确该圆的直径相当于长方形的宽是解题的关键。
12. 1080 12.56
【分析】钟面指针走一圈是360°,钟面分为12大格,1大格表示30°,时针走1大格,分针走1圈;时针从“2”走到“5”,走了3大格,分针相当于走了3圈,即360°×3=1080°。时针从“2”走到“5”,走了3大格,即30°×3=90°,相当于走了钟面的,如果时针的长度为4厘米,这段时间时针扫过的面积相当于半径为4厘米的圆的面积的,代入数据计算即可。
【详解】(5-2)×360°
=3×360°
=1080°
=50.24×
=12.56(平方厘米)
【点睛】解答本题的关键是明确时针走1大格,分针走1圈,进而利用圆的面积公式进行解答。
13.√
【分析】根据圆和正方形的周长公式分别求出直径和边长,进行比较可知本题说法正确。
【详解】因为d=C÷π,
a=C÷4,
而圆周率小于4,所以直径大于正方形的边长。
故答案为:√
【点睛】考查学生对圆的周长与直径、正方形的周长与边长之间关系知识的掌握。
14.√
【解析】略
15.×
【分析】(1)图一为外方内圆:圆的直径是1cm,根据圆面积计算公式“S=πr2”及半径与直径的关系“r=d÷2”即可求出圆的面积;正方形的边长与圆的直径相等,根据正方形的面积等于边长×边长,即可求出正方形的面积,阴影部分面积等于正方形面积减去圆的面积。
(2)图二为外圆内方:同理可求得圆的面积,正方形看作两个底为圆直径,高为圆半径的三角形,根据三角形面积计算公式“S=ah÷2”,即可求得正方形的面积。圆的面积减去正方形面积等于阴影部分面积,然后把两个图形中阴影部分面积进行比较,即可解答。
【详解】(1)图一阴影部分面积:
1×1-3.14×0.52
=1-3.14×0.25
=1-0.785
=0.215cm2
(2)图二阴影部分面积:
3.14×(0.5)2-1×0.5÷2×2
=3.14×0.25-0.5
=0.785-0.5
=0.285 cm2
0.215cm2<0.285 cm2
阴影部分的面积不相等。
故答案为:×
16.√
【解析】略
17.√
【分析】通过圆心并且两端都在圆上的线段叫做直径,所以把圆形纸对折后形成的抓痕就是圆形纸的直径,据此即可解答。
【详解】根据直径的定义可知圆心一定在直径上,而两条折痕都是圆的直径,并且两条折痕只一个交点,说明这个交点就是圆心。
故答案为:正确。
【点睛】本题考查学生对圆、圆心、直径的认识。
18.周长:37.7厘米;面积:20.75平方厘米
【分析】观察图形可知,阴影部分的面积=长方形的面积-直径是10厘米圆的面积的一半;阴影部分的周长=长方形的两条宽+长方形的一条长+直径是10厘米圆的周长的一半,根据圆的面积公式:S=πr2,圆的周长公式:C=πd,长方形的面积=长×宽,据此进行计算即可。
【详解】阴影部分的周长:
6×2+10+3.14×10÷2
=12+10+15.7
=22+15.7
=37.7(厘米)
阴影部分的面积:
10×6-3.14×(10÷2)2÷2
=60-3.14×25÷2
=60-39.25
=20.75(平方厘米)
19.15.7平方厘米;27.44平方厘米
【分析】(1)通过观察图形可知,涂色部分等于大圆面积减去小圆面积,根据圆的面积公式:S=r2代入数据即可。
(2)通过观察图形可知,涂色部分等于长方形面积减去圆的面积,长方形的宽等于圆的半径,据此解答即可。
【详解】(1)涂色部分面积为:
3.14×(6÷2)2-3.14×(4÷2)2
=3.14×32-3.14×22
=3.14×9-3.14×4
=28.26-12.56
=15.7(平方厘米)
(2)涂色部分面积为:
4×10-3.14×42×
=40-3.14×16×
=40-3.14×4
=40-12.56
=27.44(平方厘米)
20.7米
【分析】根据题意可知,一棵树的横截面的周长就是这棵树一圈的长度,用这棵树一圈长度×10,再加上72厘米,就是这根绳子的长度,据此解答。
【详解】62.8×10+72
=628+72
=700(厘米)
700厘米=7米
答:这根绳子长7米。
【点睛】解答本题的关键明确树干横截面的周长就是这棵树绕树1圈的长度。注意单位名数的换算。
21.(1)314棵;
(2)753600条
【分析】(1)沿湖的一周栽树,所以需先求出圆的周长:3.14×400=1256(米),根据植树问题:在封闭线路上植树,棵数与段数相等,即棵数=间隔数,算出间隔数即为可栽树的数量:1256÷4=314(棵);
(2),据此可求出圆的面积,再乘6即可求出湖里大约一共能养多少条鱼。
【详解】(1)3.14×400=1256(米)
1256÷4=314(棵)
答:一共要栽314棵柳树。
(2)半径:400÷2=200(米)
=3.14×
=125600(平方米)
125600×6=753600(条)
答:湖里大约一共能养753600条鱼。
【点睛】本题考查圆的周长及面积公式的应用,学生需熟练掌握圆的周长及面积公式。
22.够
【分析】根据题意,高2.5米的半圆形气球拱门,这个半圆拱门的半径是2.5米,根据半圆弧的周长公式:周长=π×半径×2÷2,代入数据,求出这个气球拱门的长度,再进行比较,如果半圆拱门的长度大于8米,就不够,如果拱门的长度小于8米,就够,据此解答。
【详解】3.14×2.5×2÷2
=7.85×2÷2
=15.7÷2
=7.85(米)
7.85<8,做半圆拱门够。
答:现在有一条长8米的气球串,做半圆形拱门够。
【点睛】熟练掌握圆的周长公式是解答本题的关键。
23.2512平方厘米
【分析】观察设计图可知,圆环的内圆直径是20厘米,则内圆半径是20÷2=10(厘米),外圆半径是10+20=30(厘米)。圆环的面积=π(R2-r2),据此代入数据计算即可求出帽檐部分的面积。
【详解】20÷2=10(厘米)
=3.14×900-3.14×100
=2826-314
=2512(平方厘米)
答:帽檐部分的面积是2512平方厘米。
【点睛】本题考查圆环面积的应用。明确圆环的内圆半径和外圆半径后,根据圆环的面积公式进行解答。
24.(1)见详解(2)画图见详解;(a+5,4)(3)见详解
【分析】(1)圆的直径是4厘米,则半径是4÷2=2(厘米),据此以点O为圆心,以2厘米为半径,用圆规画出圆形。
(2)正方形的边长是4厘米,则正方形内最大的圆的直径等于4厘米,半径是2厘米,那么圆心的位置是原来圆心向右平移了5格,据此画圆。观察圆心的位置可知,点O(a,4)在第a列第4行,向右平移5格后在第(a+5)列,第4行,据此用数对表示平移后的圆心。
(3)一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴,据此解答。
【详解】(1)4÷2=2(厘米),圆的半径是2厘米。
(2)圆心向右平移5格后在第(a+5)列、第4行,则平移后圆心的位置用数对表示为(a+5,4)。
(1)(2)(3)画图如下:
【点睛】本题考查了圆的画法、用数位表示位置、用字母表示数和对称轴的画法等。需要明确圆的半径画圆;根据数对“先列后行”的特点用数对表示位置;根据对称轴的意义画出所有对称轴。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元圆易错卷(单元测试)2023-2024学年数学五年级下册苏教版
一、选择题
1.钟面上的时针从“2”走到“5”,扫过部分是一个圆心角为( )的扇形。
A.30° B.90° C.50° D.60°
2.算式3.14×7+7×2求的是半径为7厘米的( )。
A.圆的周长 B.圆的面积
C.半圆的周长 D.半圆的面积
3.有一块面积为72平方分米的长方形钢板,用激光切割出两个圆(如图)。其中一个圆的面积是( )平方分米。
A.6π B.9π C.36 D.36π
4.明明在学习圆的周长时,把一个直径是2厘米的圆形卡片在直尺上滚动一周。下面测量最接近准确值的一次是( )。
A. B.
C. D.
5.如图,空白部分的面积和涂色部分的面积相比,结果是( )。
A.空白部分的面积大 B.涂色部分的面积大
C.两部分的面积相等 D.无法确定
6.下面五句话,正确的有( )句。
(1)任意两个素数的和都是偶数。
(2)真分数都比1小,假分数一定比1大。
(3)两个数的积一定是这两个数的公倍数。
(4)1+2+3+4+…+29的和是奇数
(5)大约1500年前,我国南北朝科学家祖冲之是世界上第一个把圆周率的值精确到小数点后7位的人。
A.1 B.2 C.3 D.4
二、填空题
7.画圆时固定的一点叫作( ),用字母( )表示;连接( )到( )任意一点的线段叫作半径,用字母( )表示;通过圆心并且两端都在( )的线段叫作( ),用字母( )表示。
8.用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是( )厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是( )厘米。
9.如下图,一块圆形铝皮的周长是18.84dm,它的半径是( )dm;从中截取一个最大的正方形,剩下阴影部分的面积是( )dm2。
10.如图,等腰直角三角形的一条腰长4厘米,阴影部分可以拼成一个半径是( )厘米的半圆,空白部分的面积是( )平方厘米。
11.用一张长为10厘米、宽为6厘米的纸剪成一个最大的圆,这个圆的面积是( )平方厘米。
12.如图钟面上显示时针从“2”走到“5”,这段时间分针一共旋转了( )°;如果时针的长度为4厘米,这段时间时针扫过的面积是( )平方厘米。(π取3.14)
三、判断题
13.如果圆和正方形的周长相等,那么圆的直径大于正方形的边长。( )
14.只要给出圆心的位置和半径的具体数值,就能画出一个圆。( )
15.如图:这两个图形中圆的直径都是1cm,那么阴影部分的面积相等。 ( )
16.两个扇形,圆心角大的扇形面积不一定大。 ( )
17.把一张圆形纸片对折后打开,换个方向再对折.两条折痕的交点就是这个圆的圆心.( )
四、计算题
18.求图形中阴影部分的周长和面积。(单位:厘米)
19.求下列图形中涂色部分的面积。(单位:厘米)
五、解答题
20.一棵树树干横截面周长是62.8厘米,一根绳子绕树10圈后还多出72厘米。这根绳子长多少米?
21.滨江公园有一个近似圆形的湖面,它的直径大约400米。
(1)沿湖的一周每隔4米栽一棵柳树,一共要栽多少棵柳树?
(2)在湖里养鱼,按每平方米水面能养6条鱼计算,湖里大约一共能养多少条鱼?
22.学校“六一”庆祝活动要搭一座高2.5米的半圆形气球拱门(如图),现在有一条长8米的气球串,做半圆形拱门够吗?
23.如图是一顶帽子的设计图(单位:厘米),帽檐部分可以看成是一个圆环,帽檐部分的面积是多少平方厘米?
24.下图每个小正方形的边长为1厘米。
(1)以点O(a,4)为圆心,画一个直径为4厘米的圆。
(2)把圆O向右平移,使圆O成为正方形内最大的圆,并画出这个圆,平移后圆心的位置用数对表示( )。
(3)画出平移后与正方形组合图形的所有对称轴。
参考答案:
1.B
【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°,据此解答即可。
【详解】钟面上时针从“2”走到“5”,走了3大格,30°×3=90°,即经过的部分是一个圆心角90°的扇形。
故答案为:B
【点睛】关键弄清时针从一个数字走到相邻的另一个数字绕中心旋转了30°。
2.C
【分析】根据半圆周长的意义:半圆的周长等于这个圆周长的一半加上一条直径的长度,据此解答。
【详解】半径为7厘米圆的周长是:3.14×7×2
半径为7厘米的半圆的周长是:
3.14×7×2÷2+7×2
=3.14×7+7×2
算式3.14×7+7×2求的是半径为7厘米的半圆的周长。
故答案为:C
【点睛】熟练掌握半圆的周长的意义、半径周长的计算公式以及应用。
3.B
【分析】根据图可知,长方形的宽是圆的直径,长方形的长是圆直径的2倍,可以设圆的半径为r分米,即长方形的宽:2r分米;长方形的长:4r分米。由于长方形的面积是72平方分米,根据长方形的面积公式:长×宽,即2r×4r=72,由此即可求出r的平方,之后再根据圆的面积公式:S=πr2,把数代入即可求解。
【详解】解:设圆的半径为r分米,长方形的宽:2r分米,长方形的长:4r分米。
2r×4r=72
8r2=72
r2=72÷8
r2=9
圆的面积:9π平方分米。
故答案为:B
【点睛】本题主要考查长方形和圆的面积公式,熟练掌握它们的面积公式并灵活运用。
4.C
【分析】根据圆的周长公式:周长=π×直径;代入数据,求出圆的周长,再进行比较,即可解答。
【详解】3.14×2=6.28(厘米)
A.7.3厘米,不符合题意;
B.5.6厘米,不符合题意;
C.6.3厘米,与6.28接近,符合题意;
D.3.5厘米,不符合题意。
故答案为:C
【点睛】利用圆的周长公式进行解答,关键是熟记公式。
5.C
【分析】设半圆的直径是4厘米,则空白部分圆的直径:4÷2=2厘米;根据圆的面积公式:面积=π×半径2,分别求出半圆的面积和空白圆的面积,进而求出涂色部分的面积,再进行比较,即可解答。
【详解】设半圆直径为4厘米,则空白圆的直径为:4÷2=2(厘米)
半圆面积:3.14×(4÷2)2÷2
=3.14×4÷2
=12.56÷2
=6.28(平方厘米)
空白圆的面积:3.14×(2÷2)2
=3.14×1
=3.14(平方厘米)
涂色部分面积:6.28-3.14=3.14(平方厘米)
3.14=3.14,空白部分面积等于涂色部分面积。
如图,空白部分的面积和涂色部分的面积相比,结果是两部分的面积相等。
故答案为:C
【点睛】熟练掌握圆的面积公式是解答本题的关键。
6.B
【分析】素数也是质数;一个数,除了1和它本身两个因数没有其它因数,这样的数叫做质数,质数+质数=奇数,质数+质数=偶数,第一小题据此判断;
分子小于分母的分数叫做真分数;分子大于或等于分母的分数叫做假分数,第二小题据此判断;
如果整数a能被整数b整除(a≠0,b≠0),a就叫做b的倍数;两个数公有的倍数叫做这两个数的公倍数,第三小题据此判断;
奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数,第四小题据此判断;
祖冲之是世界上第一个把圆周率的值精确度小数点后7位的人,第五小题据此判断。
【详解】(1)素数是质数;如,2+3=5,5是奇数,3+5=8;任意两个素数的和可能是奇数,也可能是偶数,原题干说法错误;
(2)真分数都小于1,假分数大于或等于1,原题干说法错误;
(3)因数和倍数是在整数范畴,两个小数的乘积就不是它们的公倍数,如:0.2×0.1=0.02,我们不能说0.02是0.1和0.2的公倍数,原题干说法错误;
(4)1+2+3+4+…+29,是由15个奇数相加和14个偶数相加;和是奇数,原题干说法正确;
(5)祖冲之是世界上第一个把圆周率的值精确度小数点后7位的人,原题干说法正确。
(4)(5)2句话说法正确。
下面五句话,正确的有2句话。
故答案为:B
【点睛】本题考查的知识点角度,属于基础知识,要熟练掌握。
7. 圆心 O 圆心 圆上 r 圆上 直径 d
【分析】画圆时,固定的点叫圆心,用O表示,圆心到圆上的距离是是半径,半径用r表示,圆的直径是一条经过圆心,两端在圆上的线段,直径用d表示,据此即可填空。
【详解】由分析可知:
画圆时固定的一点叫作圆心,用字母O表示;连接圆心到圆上任意一点的线段叫作半径,用字母r表示;通过圆心并且两端都在圆上的线段叫作直径,用字母d表示。
如下图所示:
【点睛】本题主要考查圆的概念,熟练掌握圆的含义是解题的关键。
8. 5 41.4
【分析】圆规两脚间的距离就是圆的半径,根据半径=直径÷2,据此求出圆规两脚间的距离;把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长比圆的周长多两条半径的长度。据此填空即可。
【详解】10÷2=5(厘米)
3.14×10+10
=31.4+10
=41.4(厘米)
用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是5厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是41.4厘米。
【点睛】本题考查圆的周长,明确圆规两脚间的距离就是圆的半径是解题的关键。
9. 3 10.26
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出半径;阴影部分面积=圆的面积-正方形面积;正方形的对角线等于圆的直径;把正方形分成两个完全相同的三角形,根据圆的面积公式:面积=π×半径2;三角形面积公式:面积=半径×直径÷2,代入数据,即可解答。
【详解】18.84÷3.14÷2
=6÷2
=3(dm)
3.14×32-3×(3×2)÷2×2
=3.14×9-3×6÷2×2
=28.26-18÷2×2
=28.26-9×2
=28.26-18
=10.26(dm2)
【点睛】利用圆的周长公式、面积公式和三角形面积公式进行解答,关键是熟记公式,灵活运用。
10. 2 1.72
【分析】根据图可知,这个是等腰直角三角形,即三个角分别为45°、45°、90°,由于三个阴影部分可以看成一个半径是2厘米的90°的扇形;和2个半径是2厘米的圆心角是45°的扇形,即90°+45°+45°=180°,则阴影部分可以拼成一个半径是2厘米的半圆;根据三角形的面积公式:底×高÷2,半圆的面积公式:S=πr2÷2,把数代入公式即可求解。
【详解】由分析可知:
90°+45°+45°=180°
即阴影部分可以拼成一个半径是2厘米的半圆
2+2=4(厘米)
4×4÷2-3.14×2×2÷2
=8-6.28
=1.72(平方厘米)
【点睛】本题主要考查三角形和半圆的面积公式,熟练掌握它们的面积公式并灵活运用。
11.28.26
【分析】由题意可知,这个最大的圆的直径相当于长方形的宽,然后根据圆的面积公式:S=πr2,据此解答即可。
【详解】3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
【点睛】本题考查圆的面积,明确该圆的直径相当于长方形的宽是解题的关键。
12. 1080 12.56
【分析】钟面指针走一圈是360°,钟面分为12大格,1大格表示30°,时针走1大格,分针走1圈;时针从“2”走到“5”,走了3大格,分针相当于走了3圈,即360°×3=1080°。时针从“2”走到“5”,走了3大格,即30°×3=90°,相当于走了钟面的,如果时针的长度为4厘米,这段时间时针扫过的面积相当于半径为4厘米的圆的面积的,代入数据计算即可。
【详解】(5-2)×360°
=3×360°
=1080°
=50.24×
=12.56(平方厘米)
【点睛】解答本题的关键是明确时针走1大格,分针走1圈,进而利用圆的面积公式进行解答。
13.√
【分析】根据圆和正方形的周长公式分别求出直径和边长,进行比较可知本题说法正确。
【详解】因为d=C÷π,
a=C÷4,
而圆周率小于4,所以直径大于正方形的边长。
故答案为:√
【点睛】考查学生对圆的周长与直径、正方形的周长与边长之间关系知识的掌握。
14.√
【解析】略
15.×
【分析】(1)图一为外方内圆:圆的直径是1cm,根据圆面积计算公式“S=πr2”及半径与直径的关系“r=d÷2”即可求出圆的面积;正方形的边长与圆的直径相等,根据正方形的面积等于边长×边长,即可求出正方形的面积,阴影部分面积等于正方形面积减去圆的面积。
(2)图二为外圆内方:同理可求得圆的面积,正方形看作两个底为圆直径,高为圆半径的三角形,根据三角形面积计算公式“S=ah÷2”,即可求得正方形的面积。圆的面积减去正方形面积等于阴影部分面积,然后把两个图形中阴影部分面积进行比较,即可解答。
【详解】(1)图一阴影部分面积:
1×1-3.14×0.52
=1-3.14×0.25
=1-0.785
=0.215cm2
(2)图二阴影部分面积:
3.14×(0.5)2-1×0.5÷2×2
=3.14×0.25-0.5
=0.785-0.5
=0.285 cm2
0.215cm2<0.285 cm2
阴影部分的面积不相等。
故答案为:×
16.√
【解析】略
17.√
【分析】通过圆心并且两端都在圆上的线段叫做直径,所以把圆形纸对折后形成的抓痕就是圆形纸的直径,据此即可解答。
【详解】根据直径的定义可知圆心一定在直径上,而两条折痕都是圆的直径,并且两条折痕只一个交点,说明这个交点就是圆心。
故答案为:正确。
【点睛】本题考查学生对圆、圆心、直径的认识。
18.周长:37.7厘米;面积:20.75平方厘米
【分析】观察图形可知,阴影部分的面积=长方形的面积-直径是10厘米圆的面积的一半;阴影部分的周长=长方形的两条宽+长方形的一条长+直径是10厘米圆的周长的一半,根据圆的面积公式:S=πr2,圆的周长公式:C=πd,长方形的面积=长×宽,据此进行计算即可。
【详解】阴影部分的周长:
6×2+10+3.14×10÷2
=12+10+15.7
=22+15.7
=37.7(厘米)
阴影部分的面积:
10×6-3.14×(10÷2)2÷2
=60-3.14×25÷2
=60-39.25
=20.75(平方厘米)
19.15.7平方厘米;27.44平方厘米
【分析】(1)通过观察图形可知,涂色部分等于大圆面积减去小圆面积,根据圆的面积公式:S=r2代入数据即可。
(2)通过观察图形可知,涂色部分等于长方形面积减去圆的面积,长方形的宽等于圆的半径,据此解答即可。
【详解】(1)涂色部分面积为:
3.14×(6÷2)2-3.14×(4÷2)2
=3.14×32-3.14×22
=3.14×9-3.14×4
=28.26-12.56
=15.7(平方厘米)
(2)涂色部分面积为:
4×10-3.14×42×
=40-3.14×16×
=40-3.14×4
=40-12.56
=27.44(平方厘米)
20.7米
【分析】根据题意可知,一棵树的横截面的周长就是这棵树一圈的长度,用这棵树一圈长度×10,再加上72厘米,就是这根绳子的长度,据此解答。
【详解】62.8×10+72
=628+72
=700(厘米)
700厘米=7米
答:这根绳子长7米。
【点睛】解答本题的关键明确树干横截面的周长就是这棵树绕树1圈的长度。注意单位名数的换算。
21.(1)314棵;
(2)753600条
【分析】(1)沿湖的一周栽树,所以需先求出圆的周长:3.14×400=1256(米),根据植树问题:在封闭线路上植树,棵数与段数相等,即棵数=间隔数,算出间隔数即为可栽树的数量:1256÷4=314(棵);
(2),据此可求出圆的面积,再乘6即可求出湖里大约一共能养多少条鱼。
【详解】(1)3.14×400=1256(米)
1256÷4=314(棵)
答:一共要栽314棵柳树。
(2)半径:400÷2=200(米)
=3.14×
=125600(平方米)
125600×6=753600(条)
答:湖里大约一共能养753600条鱼。
【点睛】本题考查圆的周长及面积公式的应用,学生需熟练掌握圆的周长及面积公式。
22.够
【分析】根据题意,高2.5米的半圆形气球拱门,这个半圆拱门的半径是2.5米,根据半圆弧的周长公式:周长=π×半径×2÷2,代入数据,求出这个气球拱门的长度,再进行比较,如果半圆拱门的长度大于8米,就不够,如果拱门的长度小于8米,就够,据此解答。
【详解】3.14×2.5×2÷2
=7.85×2÷2
=15.7÷2
=7.85(米)
7.85<8,做半圆拱门够。
答:现在有一条长8米的气球串,做半圆形拱门够。
【点睛】熟练掌握圆的周长公式是解答本题的关键。
23.2512平方厘米
【分析】观察设计图可知,圆环的内圆直径是20厘米,则内圆半径是20÷2=10(厘米),外圆半径是10+20=30(厘米)。圆环的面积=π(R2-r2),据此代入数据计算即可求出帽檐部分的面积。
【详解】20÷2=10(厘米)
=3.14×900-3.14×100
=2826-314
=2512(平方厘米)
答:帽檐部分的面积是2512平方厘米。
【点睛】本题考查圆环面积的应用。明确圆环的内圆半径和外圆半径后,根据圆环的面积公式进行解答。
24.(1)见详解(2)画图见详解;(a+5,4)(3)见详解
【分析】(1)圆的直径是4厘米,则半径是4÷2=2(厘米),据此以点O为圆心,以2厘米为半径,用圆规画出圆形。
(2)正方形的边长是4厘米,则正方形内最大的圆的直径等于4厘米,半径是2厘米,那么圆心的位置是原来圆心向右平移了5格,据此画圆。观察圆心的位置可知,点O(a,4)在第a列第4行,向右平移5格后在第(a+5)列,第4行,据此用数对表示平移后的圆心。
(3)一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴,据此解答。
【详解】(1)4÷2=2(厘米),圆的半径是2厘米。
(2)圆心向右平移5格后在第(a+5)列、第4行,则平移后圆心的位置用数对表示为(a+5,4)。
(1)(2)(3)画图如下:
【点睛】本题考查了圆的画法、用数位表示位置、用字母表示数和对称轴的画法等。需要明确圆的半径画圆;根据数对“先列后行”的特点用数对表示位置;根据对称轴的意义画出所有对称轴。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
