第七章平面直角坐标系 素养提升练习卷(含解析)数学人教版七年级下册
文档属性
| 名称 | 第七章平面直角坐标系 素养提升练习卷(含解析)数学人教版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 19:01:34 | ||
图片预览



文档简介
第七章平面直角坐标系素养提升练习卷
时间:90分钟 满分:100分
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)下列数据中不能确定物体的位置的是( )
A.单元号 B.北偏东 C.清风路号 D.电影院排号
2.(本题3分)已知平面直角坐标系中,点的坐标为,则下列关于点的说法中,正确的是( )
A.点在第二象限 B.点到轴的距离为2
C.点的横、纵坐标可能相等 D.点不可能在坐标轴上
3.(本题3分)如图,这是画在方格纸上的江西部分旅游景点简图,建立平面直角坐标系后,明月山的坐标为,井冈山的坐标为,则滕王阁的坐标为( )
A. B. C. D.
4.(本题3分)在平面直角坐标系中,下列说法:①若点在坐标轴上,则;②若为任意实数,则点一定在第一象限;③若点到轴的距离是到轴距离的2倍,则符合条件的点有4个;④已知点,点,则轴.其中正确的是( )
A.①④ B.②③ C.①③④ D.①②③④
5.(本题3分)已知点在轴上,点在轴上,则点坐标为( )
A. B. C. D.
6.(本题3分)平面直角坐标系中,第四象限内有一点,过点作轴于,作轴于,已知,,则点的坐标为( )
A. B. C. D.
7.(本题3分)在平面直角坐标系中,点的坐标为,轴,且,则点的坐标为( )
A. B. C.或 D.或
8.(本题3分)已知三角形的三个顶点坐标分别是、、,把三角形移动到一个确定位置,平移后各对应点的坐标可能是( )
A.、、 B.、、
C.、、 D.、、
9.(本题3分)已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a-c|+=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为( )
A.12 B.14 C.16 D.20
10.(本题3分)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点,…,则点的坐标是( )
A.(674,1) B.(675,1) C. D.(673,1)
评卷人得分
二、填空题(共21分)
11.(本题3分)如图,五子棋的比赛规则是只要相邻同色5子先成一条直线就算胜,如图是两人玩的一盘棋,若白①的位置是,黑②的位置是,现轮到白棋走,则白棋放在 (填坐标)位置就获得胜利了.
12.(本题3分)如图,第一象限内有两点,,将线段平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
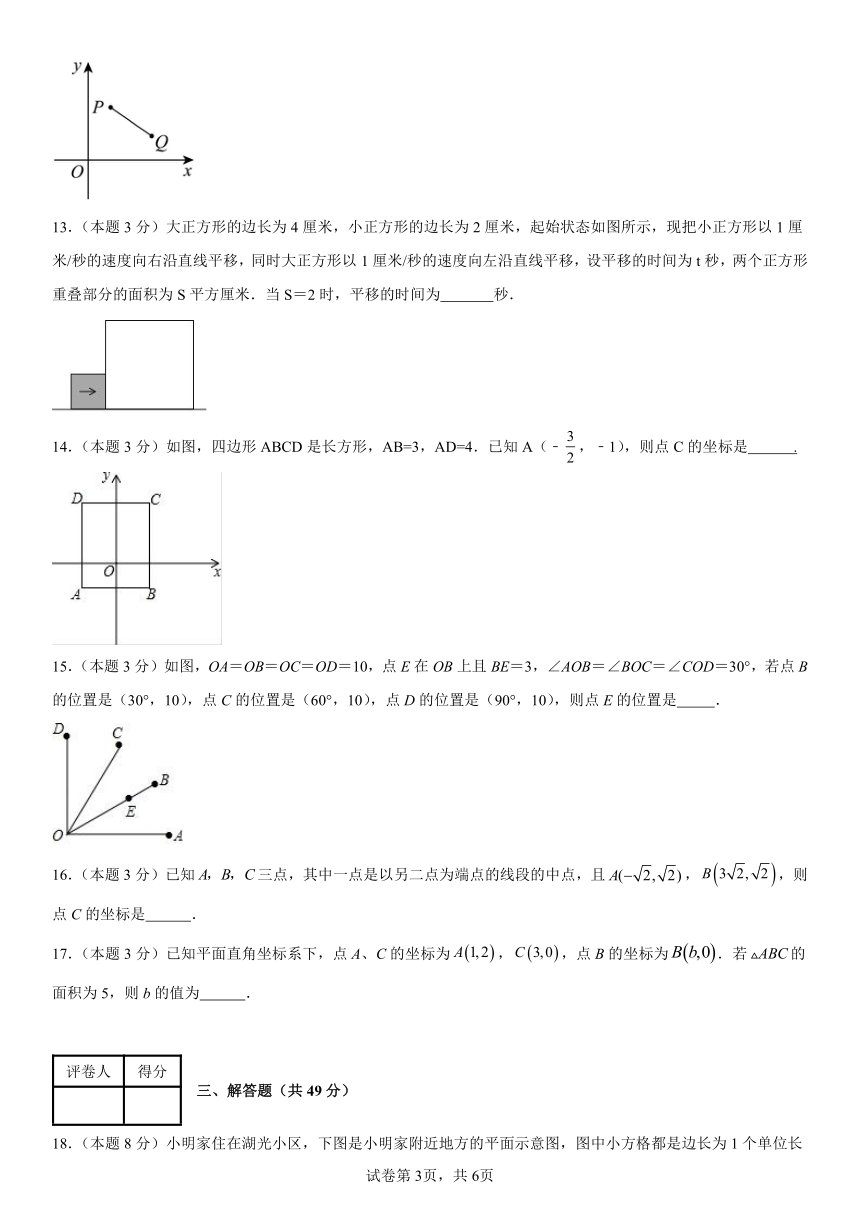
13.(本题3分)大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,现把小正方形以1厘米/秒的速度向右沿直线平移,同时大正方形以1厘米/秒的速度向左沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,平移的时间为 秒.
14.(本题3分)如图,四边形ABCD是长方形,AB=3,AD=4.已知A(﹣,﹣1),则点C的坐标是 .
15.(本题3分)如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是 .
16.(本题3分)已知三点,其中一点是以另二点为端点的线段的中点,且,,则点C的坐标是 .
17.(本题3分)已知平面直角坐标系下,点A、C的坐标为,,点B的坐标为.若的面积为5,则b的值为 .
评卷人得分
三、解答题(共49分)
18.(本题8分)小明家住在湖光小区,下图是小明家附近地方的平面示意图,图中小方格都是边长为1个单位长度的正方形,其中第一中学的坐标为,康德乐的坐标为.
(1)请在图中画出平面直角坐标系,并写出学管中心的坐标:______
(2)若大世界的坐标为,请在坐标系中用点P表示它的位置;
(3)小明家从湖光小区搬家到府前官邸,请你用坐标描述平移的过程.
19.(本题8分)如图,已知四边形,将四边形平移到四边形,其中顶点的对应点的坐标为.
(1)求四边形的面积;
(2)画出平移后的四边形,顶点的坐标为,顶点的坐标为______;
(3)连接,在轴上找一点,使得以,,为顶点的三角形的面积为10,求满足条件的点的坐标.
20.(本题8分)已知在y轴负半轴上,直线轴,且线段长度为4.
(1)求点M的坐标;
(2)求的值;
(3)求N点坐标.
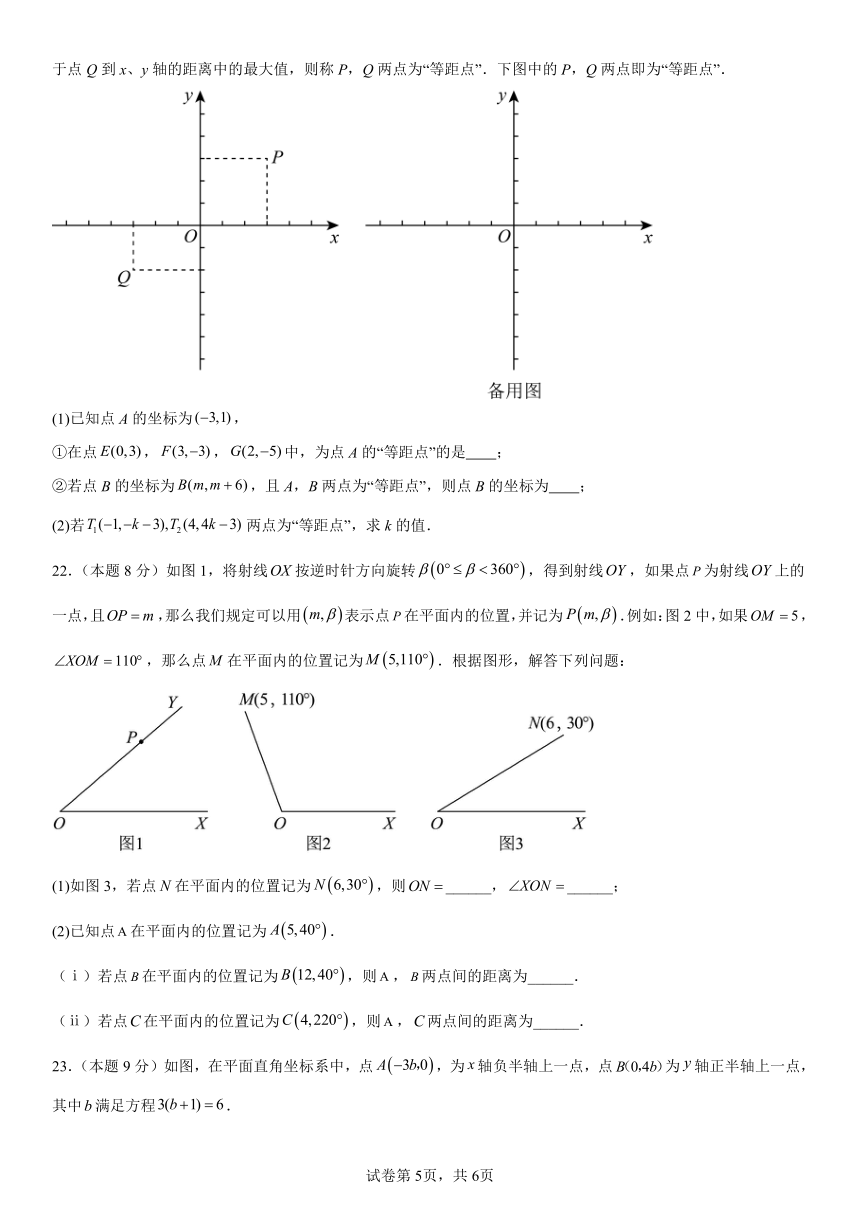
21.(本题8分)在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.
(1)已知点A的坐标为,
①在点,,中,为点A的“等距点”的是 ;
②若点B的坐标为,且A,B两点为“等距点”,则点B的坐标为 ;
(2)若两点为“等距点”,求k的值.
22.(本题8分)如图1,将射线按逆时针方向旋转,得到射线,如果点为射线上的一点,且,那么我们规定可以用表示点在平面内的位置,并记为.例如:图2中,如果,,那么点在平面内的位置记为.根据图形,解答下列问题:
(1)如图3,若点在平面内的位置记为,则______,______;
(2)已知点在平面内的位置记为.
(ⅰ)若点在平面内的位置记为,则,两点间的距离为______.
(ⅱ)若点在平面内的位置记为,则,两点间的距离为______.
23.(本题9分)如图,在平面直角坐标系中,点,为轴负半轴上一点,点为轴正半轴上一点,其中满足方程.
(1)求点、的坐标;
(2)点为轴负半轴上一点,且的面积为,求点的坐标;
(3)在轴上是否存在一点,使的面积等于的面积的一半,若存在,求出相应的点的坐标,若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了坐标确定点的位置,确定一个物体的位置,要用一个有序数对,即用两个数据.找到一个数据的选项即为所求.
【详解】解:A、单元号,是有序数对,能确定物体的位置,故本选项不合题意;
B、北偏东,不是有序数对,不能确定物体的位置,故本选项符合题意;
C、清风路号,“清风路”相当于一个数据,是有序数对,能确定物体的位置,故本选项不合题意;
D、电影院排号,是有序数对,能确定物体的位置,故本选项不合题意;
故选:B.
2.D
【分析】本题主要考查了点的坐标,根据点的坐标特点逐一解答即可.
【详解】解:点的坐标为,
∵,
∴点不可能在第二象限,故选项A说法错误;
点也不可能在坐标轴上,选项D说法正确;
点到轴的距离为3,故选项B说法错误;
若,即,不成立,故点的横、纵坐标不可能相等,
故选项C说法错误;
故选:D.
3.D
【分析】本题考查用坐标表示实际位置,根据已知点的坐标确定原点的位置,建立直角坐标系,求解即可.
【详解】解:由题意,建立如下坐标系:
由图可知:滕王阁的坐标为;
故选D.
4.A
【分析】本题考查了平面直角坐标系内的坐标特征,平面直角坐标系内点到坐标轴的距离,平行于坐标轴的特征,①根据坐标轴上点的坐标特征即可判断;②根据第一象限的坐标特征即可判断;③根据到坐标轴的距离即可得到结果;④根据平行坐标轴的坐标特征即可得到结果;掌握平面直角坐标系内点的特征是解题的关键.
【详解】解:∵点在坐标轴上,
∴或,
∴,
故①正确;
∵为任意实数,
∴当时,点在坐标轴上,
故②错误;
点到轴的距离是到轴距离的2倍,
只需横坐标的绝对值是纵坐标绝对值的2倍即可,这样的点不止4个,
故③错误;
∵点,点,
∴点M、N在直线上,
∴轴,
故④正确;
∴正确的序号有:①④,
故选:A.
5.C
【分析】本题考查了坐标与图形,轴上的点,其横坐标为零;轴上的点,其纵坐标为零,据此即可求解
【详解】解:由题意得:
∴,
∴点坐标为
故选:C
6.B
【分析】本题考查了点到坐标轴的距离以及点的坐标,根据第四象限的点,得出点的横坐标为正数,纵坐标为负数,结合“过点作轴于,作轴于,已知,,”这个条件即可作答.
【详解】解:∵点在第四象限内,
∴点的横坐标为正数,纵坐标为负数,
∵过点作轴于,作轴于,已知,,
∴点的坐标为,
故选:B.
7.D
【分析】本题考查了坐标与图形,根据轴,可得B点纵坐标,再根据,可以得到可以得到B点位于A左右两边的两个坐标点.
【详解】解:点的坐标为,轴,
点的纵坐标与点的纵坐标相等为3,
点的横坐标为或,
点的坐标为或,
故选:D.
8.B
【分析】本题考查平移的性质,移后各顶点的坐标与原顶点坐标相比,必须有统一的变化规律,即每个顶点的横坐标要有相同的变化,纵坐标也有相同的变化.
【详解】解:将平移,结合图形平移的规律可知:点A、B、C平移的规律是相同的.
A.,,平移方向不同,不符合题意;
B.横坐标变化:,,,纵坐标变化:,,,符合题意;
C.,,平移距离不同,不符合题意;
D.,,平移方向不同,不符合题意;
故选:B.
9.C
【分析】有非负数的性质得到a=c,b=8,,PQ∥y轴,由于其扫过的图形是矩形可求得,代入即可求得结论.
【详解】解:|a-c|+=0,
∴a=c,b=8,
,PQ∥y轴,
∴PQ=8-2=6,
将线段PQ向右平移a个单位长度,其扫过的图形是边长为a和6的矩形,
,
∴a=4,
∴c=4,
∴a+b+c=4+8+4=16;
故选:C.
【点睛】本题主要考查了非负数的性质,坐标的平移,矩形的性质,能根据点的坐标判断出PQ∥y轴,进而求得PQ是解题的关键.
10.B
【分析】本题属于平面直角坐标系中找点的规律问题,先根据,可得,再根据,即可推出的坐标,找到某种循环规律之后,可以得解.
【详解】解:由图可得,,
,
,
,
故选:B.
11.
【分析】本题考查了利用坐标确定位置,确定坐标轴的位置是解题的关键.根据①②两棋的位置可确定坐标轴的位置,然后根据比赛规则,确定白棋位置即可.
【详解】解:根据白①的位置是,黑②的位置是,
可确定坐标系如下图,
当白棋放在位置时,白棋可5子成一条直线,即可获得胜利.
故答案为:.
12.或.
【分析】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
设平移后点P、Q的对应点分别是.分两种情况进行讨论:①在y轴上,在x轴上;②在x轴上,在y轴上.
【详解】解:设平移后点P、Q的对应点分别是.
分两种情况:
①在y轴上,在x轴上,
则横坐标为0,纵坐标为0,
∴,
∴点P平移后的对应点的坐标是;
②在x轴上,在y轴上,
则纵坐标为0,横坐标为0,
∴,
∴点P平移后的对应点的坐标是;
综上可知,点P平移后的对应点的坐标是或.
故答案为:或.
13.或
【分析】先求出重叠部分长方形的宽,分重叠部分在大正方形的左边和右边两种情况讨论,根据“时间”求解.
【详解】当时,重叠部分长方形的宽,
重叠部分在大正方形的左边时,秒,
重叠部分在大正方形的右边时,t=秒,
综上所述,小正方形平移的时间为或秒.
故答案为:或.
【点睛】本题考查了平移的性质,主要利用了长方形的面积,关键是掌握公式“时间=”,难点在于分两种情况解答.
14.(,3)
【分析】由矩形的性质可知CD=AB= 3,BC=AD= 4,结合A点坐标即可求得C点坐标.
【详解】∵四边形ABCD是长方形,
∴CD=AB= 3,BC=AD= 4,
∵点A(﹣,﹣1),
∴点C的坐标为(﹣+3,﹣1+4),
即点C的坐标为(,3),
【点睛】本题考查了矩形的性质和坐标的平移,根据平移的性质解决问题是解答此题的关键.
15.(30°,7).
【分析】根据题意得出OE的长,再利用点B,C的位置以及其坐标的特点得出E点坐标.
【详解】∵BO=10,BE=3,
∴OE=7,
∵∠AOB=30°,
∴点E的位置是:(30°,7).
故答案是:(30°,7).
【点睛】此题考查线段的和差计算,点位置的表示方法,正确理解题意是解题的关键.
16.或或
【分析】本题考查了中点坐标的计算,设,分三种情况:若为的中点;若为的中点;若为的中点;分别求解即可.
【详解】解:设,
若为的中点,则,,即;
若为的中点,则,,即;
若为的中点,则,,即;
综上所述,点C的坐标是或或,
故答案为:或或.
17.8或
【分析】本题考查了平面直角坐标系中的坐标与图形,利用横、纵坐标得到线段的长度解题的关键.
根据点B、C的坐标三角形的底,根据点A的坐标可知边上的高,利用三角形面积计算公式求解即可.
【详解】点A、C的坐标为,,点B的坐标为,
的底为,高为2,
的面积为5,
,
,
或,
故答案为:8或.
18.(1)画图见解析,
(2)见解析
(3)(0,0)→(2,0)→(2,-3)(答案不唯一)
【分析】(1)以湖光小区为原点,向东和向北为横纵轴的正方向建立坐标系,写出坐标即可;
(2)关键坐标描出点P即可;
(3)根据向右平移两个单位,向下平移3个单位,用坐标描述即可.
【详解】(1)解:因为,第一中学的坐标为,康德乐的坐标为,
所以以湖光小区为原点,向东和向北为横纵轴的正方向建立坐标系,
学管中心的坐标为.
(2)解:大世界的坐标为,在平面直角坐标系中位置如图所示:
(3)解:小明家从湖光小区搬家到府前官邸,横坐标加2,纵坐标减3.
用坐标描述平移的过程为:(0,0)→(2,0)→(2,-3)(答案不唯一).
【点睛】本题考查了用平面直角坐标系表示位置,解题关键是根据坐标建立平面直角坐标系,会利用点的坐标表示不同位置.
19.(1)
(2)图见解析,
(3)或.
【分析】本题考查坐标与图形,坐标与平移,掌握分割法求面积,以及平移的性质,是解题的关键.
(1)分割法求出三角形的面积即可;
(2)根据平移的性质,画出四边形,进而写出顶点的坐标即可;
(3)设,利用三角形的面积公式进行计算即可.
【详解】(1)解:.
(2)平移后的四边形如图所示,顶点的坐标为
(3)由题可知,点的坐标为,点到轴的距离为5,
设点的坐标为,则
,解得.
所以点的坐标为或.
20.(1)
(2)2
(3)或
【分析】本题考查了坐标与图形性质,明确平面直角坐标系中点的坐标特点是解题的关键.
(1)由点M在y轴负半轴上,可得点M的横坐标等于0,列出关于a的绝对值方程,可解得a的值,则点M的坐标可求得;
(2)将(1)中所求得的a的值代入计算即可;
(3)由直线轴及点M的坐标,可设,结合线段长度为4,可得关于x的方程,解得x的值,则点N的坐标可得.
【详解】(1)解:在y轴负半轴上,
,
当时,,
当时,,
,
,
点M的坐标为.
(2)解:,
(3)解: 直线轴,点M的坐标为,
设点N的坐标为,
又 线段长度为4,
,
点N的坐标为或.
21.(1)①E、F;②
(2)1或2
【分析】本题主要考查了坐标与图形性质,此题属于阅读理解类型题目,首先读懂“等距点”的定义,而后根据概念解决问题,难度较大,需要有扎实的基础,培养了阅读理解、迁移运用的能力.
(1)①找到x、y轴距离最大为3的点即可;
②先分析出直线上的点到x、y轴距离中有3的点,再根据“等距点”概念进行解答即可;
(2)先分析出直线上的点到x、y轴距离中有4的点,再根据“等距点”概念进行解答即可.
【详解】(1)①点到x、y轴的距离中最大值为3,
与A点是“等距点”的点是E、F.
②当点B坐标中到x、y轴距离其中至少有一个为3的点有,
这些点中与A符合“等距点”的是.
故答案为①E、F;②;
(2)两点为“等距点”,
①若时,则或
解得(舍去)或.
②若时,则
解得或(舍去).
根据“等距点”的定义知,或符合题意.
即k的值是1或2.
22.(1)6,
(2)(ⅰ)7(ⅱ)9
【分析】本题考查用坐标表示位置,掌握题干给定的表示方法,是解题的关键:
(1)根据给定的坐标的的表示方法,进行作答即可;
(2)(ⅰ)由题意,可知,在一条直线上且在点同侧,横坐标之差即为,两点间的距离;
(ⅱ)由题意,可知,在一条直线上,横坐标之差即为,两点间的距离;
【详解】(1)解:∵,
∴,
故答案为:;
(2)(ⅰ)如图,
∵,,
∴三点共线,在点的同侧,
∴;
故答案为:7;
(ⅱ)如图:
由题意,得:,
∴三点共线,且在点的两侧,
∴;
故答案为:9.
23.(1)点A坐标为(-3,0),点B坐标为(0,4);(2)点C坐标为(0,-4);(3)存在,点P坐标为(,0)或(-,0).
【分析】(1)解方程可求出b的值,即可得A、B坐标;
(2)根据A、B坐标可得OA、OB的长,利用三角形面积公式可求出BC的长,根据点C在y轴负半轴可得OC的长,可得C点坐标;
(3)利用三角形面积公式可求出OP的长,分点P在原点左边和右边两种情况,求出OP的坐标即可.
【详解】(1)∵,
∴b=1,
∵,,
∴点A坐标为(-3,0),点B坐标为(0,4).
(2)如图,∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∵△ABC的面积为12,
∴BC·OA=12,即×3×BC=12,
解得:BC=8,
∵点为轴负半轴上一点,
∴OC=BC-OB=8-4=4,
∴点C坐标为(0,-4).
(3)如图,∵的面积等于的面积的一半,△ABC的面积为12,
∴△PBC的面积为6,
∴BC·OP=6,即×8×OP=6,
解得:OP=,
当点P在原点左边时,点P坐标为(-,0),
当点P在原点右边时,点P坐标为(,0),
∴存在一点,使的面积等于的面积的一半,点P坐标为(,0)或(-,0).
【点睛】本题考查坐标与图形的性质及三角形的面积,运用分类讨论的思想是解题关键.
答案第1页,共2页
答案第1页,共2页
时间:90分钟 满分:100分
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)下列数据中不能确定物体的位置的是( )
A.单元号 B.北偏东 C.清风路号 D.电影院排号
2.(本题3分)已知平面直角坐标系中,点的坐标为,则下列关于点的说法中,正确的是( )
A.点在第二象限 B.点到轴的距离为2
C.点的横、纵坐标可能相等 D.点不可能在坐标轴上
3.(本题3分)如图,这是画在方格纸上的江西部分旅游景点简图,建立平面直角坐标系后,明月山的坐标为,井冈山的坐标为,则滕王阁的坐标为( )
A. B. C. D.
4.(本题3分)在平面直角坐标系中,下列说法:①若点在坐标轴上,则;②若为任意实数,则点一定在第一象限;③若点到轴的距离是到轴距离的2倍,则符合条件的点有4个;④已知点,点,则轴.其中正确的是( )
A.①④ B.②③ C.①③④ D.①②③④
5.(本题3分)已知点在轴上,点在轴上,则点坐标为( )
A. B. C. D.
6.(本题3分)平面直角坐标系中,第四象限内有一点,过点作轴于,作轴于,已知,,则点的坐标为( )
A. B. C. D.
7.(本题3分)在平面直角坐标系中,点的坐标为,轴,且,则点的坐标为( )
A. B. C.或 D.或
8.(本题3分)已知三角形的三个顶点坐标分别是、、,把三角形移动到一个确定位置,平移后各对应点的坐标可能是( )
A.、、 B.、、
C.、、 D.、、
9.(本题3分)已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a-c|+=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为( )
A.12 B.14 C.16 D.20
10.(本题3分)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点,…,则点的坐标是( )
A.(674,1) B.(675,1) C. D.(673,1)
评卷人得分
二、填空题(共21分)
11.(本题3分)如图,五子棋的比赛规则是只要相邻同色5子先成一条直线就算胜,如图是两人玩的一盘棋,若白①的位置是,黑②的位置是,现轮到白棋走,则白棋放在 (填坐标)位置就获得胜利了.
12.(本题3分)如图,第一象限内有两点,,将线段平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
13.(本题3分)大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,现把小正方形以1厘米/秒的速度向右沿直线平移,同时大正方形以1厘米/秒的速度向左沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,平移的时间为 秒.
14.(本题3分)如图,四边形ABCD是长方形,AB=3,AD=4.已知A(﹣,﹣1),则点C的坐标是 .
15.(本题3分)如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是 .
16.(本题3分)已知三点,其中一点是以另二点为端点的线段的中点,且,,则点C的坐标是 .
17.(本题3分)已知平面直角坐标系下,点A、C的坐标为,,点B的坐标为.若的面积为5,则b的值为 .
评卷人得分
三、解答题(共49分)
18.(本题8分)小明家住在湖光小区,下图是小明家附近地方的平面示意图,图中小方格都是边长为1个单位长度的正方形,其中第一中学的坐标为,康德乐的坐标为.
(1)请在图中画出平面直角坐标系,并写出学管中心的坐标:______
(2)若大世界的坐标为,请在坐标系中用点P表示它的位置;
(3)小明家从湖光小区搬家到府前官邸,请你用坐标描述平移的过程.
19.(本题8分)如图,已知四边形,将四边形平移到四边形,其中顶点的对应点的坐标为.
(1)求四边形的面积;
(2)画出平移后的四边形,顶点的坐标为,顶点的坐标为______;
(3)连接,在轴上找一点,使得以,,为顶点的三角形的面积为10,求满足条件的点的坐标.
20.(本题8分)已知在y轴负半轴上,直线轴,且线段长度为4.
(1)求点M的坐标;
(2)求的值;
(3)求N点坐标.
21.(本题8分)在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.
(1)已知点A的坐标为,
①在点,,中,为点A的“等距点”的是 ;
②若点B的坐标为,且A,B两点为“等距点”,则点B的坐标为 ;
(2)若两点为“等距点”,求k的值.
22.(本题8分)如图1,将射线按逆时针方向旋转,得到射线,如果点为射线上的一点,且,那么我们规定可以用表示点在平面内的位置,并记为.例如:图2中,如果,,那么点在平面内的位置记为.根据图形,解答下列问题:
(1)如图3,若点在平面内的位置记为,则______,______;
(2)已知点在平面内的位置记为.
(ⅰ)若点在平面内的位置记为,则,两点间的距离为______.
(ⅱ)若点在平面内的位置记为,则,两点间的距离为______.
23.(本题9分)如图,在平面直角坐标系中,点,为轴负半轴上一点,点为轴正半轴上一点,其中满足方程.
(1)求点、的坐标;
(2)点为轴负半轴上一点,且的面积为,求点的坐标;
(3)在轴上是否存在一点,使的面积等于的面积的一半,若存在,求出相应的点的坐标,若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了坐标确定点的位置,确定一个物体的位置,要用一个有序数对,即用两个数据.找到一个数据的选项即为所求.
【详解】解:A、单元号,是有序数对,能确定物体的位置,故本选项不合题意;
B、北偏东,不是有序数对,不能确定物体的位置,故本选项符合题意;
C、清风路号,“清风路”相当于一个数据,是有序数对,能确定物体的位置,故本选项不合题意;
D、电影院排号,是有序数对,能确定物体的位置,故本选项不合题意;
故选:B.
2.D
【分析】本题主要考查了点的坐标,根据点的坐标特点逐一解答即可.
【详解】解:点的坐标为,
∵,
∴点不可能在第二象限,故选项A说法错误;
点也不可能在坐标轴上,选项D说法正确;
点到轴的距离为3,故选项B说法错误;
若,即,不成立,故点的横、纵坐标不可能相等,
故选项C说法错误;
故选:D.
3.D
【分析】本题考查用坐标表示实际位置,根据已知点的坐标确定原点的位置,建立直角坐标系,求解即可.
【详解】解:由题意,建立如下坐标系:
由图可知:滕王阁的坐标为;
故选D.
4.A
【分析】本题考查了平面直角坐标系内的坐标特征,平面直角坐标系内点到坐标轴的距离,平行于坐标轴的特征,①根据坐标轴上点的坐标特征即可判断;②根据第一象限的坐标特征即可判断;③根据到坐标轴的距离即可得到结果;④根据平行坐标轴的坐标特征即可得到结果;掌握平面直角坐标系内点的特征是解题的关键.
【详解】解:∵点在坐标轴上,
∴或,
∴,
故①正确;
∵为任意实数,
∴当时,点在坐标轴上,
故②错误;
点到轴的距离是到轴距离的2倍,
只需横坐标的绝对值是纵坐标绝对值的2倍即可,这样的点不止4个,
故③错误;
∵点,点,
∴点M、N在直线上,
∴轴,
故④正确;
∴正确的序号有:①④,
故选:A.
5.C
【分析】本题考查了坐标与图形,轴上的点,其横坐标为零;轴上的点,其纵坐标为零,据此即可求解
【详解】解:由题意得:
∴,
∴点坐标为
故选:C
6.B
【分析】本题考查了点到坐标轴的距离以及点的坐标,根据第四象限的点,得出点的横坐标为正数,纵坐标为负数,结合“过点作轴于,作轴于,已知,,”这个条件即可作答.
【详解】解:∵点在第四象限内,
∴点的横坐标为正数,纵坐标为负数,
∵过点作轴于,作轴于,已知,,
∴点的坐标为,
故选:B.
7.D
【分析】本题考查了坐标与图形,根据轴,可得B点纵坐标,再根据,可以得到可以得到B点位于A左右两边的两个坐标点.
【详解】解:点的坐标为,轴,
点的纵坐标与点的纵坐标相等为3,
点的横坐标为或,
点的坐标为或,
故选:D.
8.B
【分析】本题考查平移的性质,移后各顶点的坐标与原顶点坐标相比,必须有统一的变化规律,即每个顶点的横坐标要有相同的变化,纵坐标也有相同的变化.
【详解】解:将平移,结合图形平移的规律可知:点A、B、C平移的规律是相同的.
A.,,平移方向不同,不符合题意;
B.横坐标变化:,,,纵坐标变化:,,,符合题意;
C.,,平移距离不同,不符合题意;
D.,,平移方向不同,不符合题意;
故选:B.
9.C
【分析】有非负数的性质得到a=c,b=8,,PQ∥y轴,由于其扫过的图形是矩形可求得,代入即可求得结论.
【详解】解:|a-c|+=0,
∴a=c,b=8,
,PQ∥y轴,
∴PQ=8-2=6,
将线段PQ向右平移a个单位长度,其扫过的图形是边长为a和6的矩形,
,
∴a=4,
∴c=4,
∴a+b+c=4+8+4=16;
故选:C.
【点睛】本题主要考查了非负数的性质,坐标的平移,矩形的性质,能根据点的坐标判断出PQ∥y轴,进而求得PQ是解题的关键.
10.B
【分析】本题属于平面直角坐标系中找点的规律问题,先根据,可得,再根据,即可推出的坐标,找到某种循环规律之后,可以得解.
【详解】解:由图可得,,
,
,
,
故选:B.
11.
【分析】本题考查了利用坐标确定位置,确定坐标轴的位置是解题的关键.根据①②两棋的位置可确定坐标轴的位置,然后根据比赛规则,确定白棋位置即可.
【详解】解:根据白①的位置是,黑②的位置是,
可确定坐标系如下图,
当白棋放在位置时,白棋可5子成一条直线,即可获得胜利.
故答案为:.
12.或.
【分析】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
设平移后点P、Q的对应点分别是.分两种情况进行讨论:①在y轴上,在x轴上;②在x轴上,在y轴上.
【详解】解:设平移后点P、Q的对应点分别是.
分两种情况:
①在y轴上,在x轴上,
则横坐标为0,纵坐标为0,
∴,
∴点P平移后的对应点的坐标是;
②在x轴上,在y轴上,
则纵坐标为0,横坐标为0,
∴,
∴点P平移后的对应点的坐标是;
综上可知,点P平移后的对应点的坐标是或.
故答案为:或.
13.或
【分析】先求出重叠部分长方形的宽,分重叠部分在大正方形的左边和右边两种情况讨论,根据“时间”求解.
【详解】当时,重叠部分长方形的宽,
重叠部分在大正方形的左边时,秒,
重叠部分在大正方形的右边时,t=秒,
综上所述,小正方形平移的时间为或秒.
故答案为:或.
【点睛】本题考查了平移的性质,主要利用了长方形的面积,关键是掌握公式“时间=”,难点在于分两种情况解答.
14.(,3)
【分析】由矩形的性质可知CD=AB= 3,BC=AD= 4,结合A点坐标即可求得C点坐标.
【详解】∵四边形ABCD是长方形,
∴CD=AB= 3,BC=AD= 4,
∵点A(﹣,﹣1),
∴点C的坐标为(﹣+3,﹣1+4),
即点C的坐标为(,3),
【点睛】本题考查了矩形的性质和坐标的平移,根据平移的性质解决问题是解答此题的关键.
15.(30°,7).
【分析】根据题意得出OE的长,再利用点B,C的位置以及其坐标的特点得出E点坐标.
【详解】∵BO=10,BE=3,
∴OE=7,
∵∠AOB=30°,
∴点E的位置是:(30°,7).
故答案是:(30°,7).
【点睛】此题考查线段的和差计算,点位置的表示方法,正确理解题意是解题的关键.
16.或或
【分析】本题考查了中点坐标的计算,设,分三种情况:若为的中点;若为的中点;若为的中点;分别求解即可.
【详解】解:设,
若为的中点,则,,即;
若为的中点,则,,即;
若为的中点,则,,即;
综上所述,点C的坐标是或或,
故答案为:或或.
17.8或
【分析】本题考查了平面直角坐标系中的坐标与图形,利用横、纵坐标得到线段的长度解题的关键.
根据点B、C的坐标三角形的底,根据点A的坐标可知边上的高,利用三角形面积计算公式求解即可.
【详解】点A、C的坐标为,,点B的坐标为,
的底为,高为2,
的面积为5,
,
,
或,
故答案为:8或.
18.(1)画图见解析,
(2)见解析
(3)(0,0)→(2,0)→(2,-3)(答案不唯一)
【分析】(1)以湖光小区为原点,向东和向北为横纵轴的正方向建立坐标系,写出坐标即可;
(2)关键坐标描出点P即可;
(3)根据向右平移两个单位,向下平移3个单位,用坐标描述即可.
【详解】(1)解:因为,第一中学的坐标为,康德乐的坐标为,
所以以湖光小区为原点,向东和向北为横纵轴的正方向建立坐标系,
学管中心的坐标为.
(2)解:大世界的坐标为,在平面直角坐标系中位置如图所示:
(3)解:小明家从湖光小区搬家到府前官邸,横坐标加2,纵坐标减3.
用坐标描述平移的过程为:(0,0)→(2,0)→(2,-3)(答案不唯一).
【点睛】本题考查了用平面直角坐标系表示位置,解题关键是根据坐标建立平面直角坐标系,会利用点的坐标表示不同位置.
19.(1)
(2)图见解析,
(3)或.
【分析】本题考查坐标与图形,坐标与平移,掌握分割法求面积,以及平移的性质,是解题的关键.
(1)分割法求出三角形的面积即可;
(2)根据平移的性质,画出四边形,进而写出顶点的坐标即可;
(3)设,利用三角形的面积公式进行计算即可.
【详解】(1)解:.
(2)平移后的四边形如图所示,顶点的坐标为
(3)由题可知,点的坐标为,点到轴的距离为5,
设点的坐标为,则
,解得.
所以点的坐标为或.
20.(1)
(2)2
(3)或
【分析】本题考查了坐标与图形性质,明确平面直角坐标系中点的坐标特点是解题的关键.
(1)由点M在y轴负半轴上,可得点M的横坐标等于0,列出关于a的绝对值方程,可解得a的值,则点M的坐标可求得;
(2)将(1)中所求得的a的值代入计算即可;
(3)由直线轴及点M的坐标,可设,结合线段长度为4,可得关于x的方程,解得x的值,则点N的坐标可得.
【详解】(1)解:在y轴负半轴上,
,
当时,,
当时,,
,
,
点M的坐标为.
(2)解:,
(3)解: 直线轴,点M的坐标为,
设点N的坐标为,
又 线段长度为4,
,
点N的坐标为或.
21.(1)①E、F;②
(2)1或2
【分析】本题主要考查了坐标与图形性质,此题属于阅读理解类型题目,首先读懂“等距点”的定义,而后根据概念解决问题,难度较大,需要有扎实的基础,培养了阅读理解、迁移运用的能力.
(1)①找到x、y轴距离最大为3的点即可;
②先分析出直线上的点到x、y轴距离中有3的点,再根据“等距点”概念进行解答即可;
(2)先分析出直线上的点到x、y轴距离中有4的点,再根据“等距点”概念进行解答即可.
【详解】(1)①点到x、y轴的距离中最大值为3,
与A点是“等距点”的点是E、F.
②当点B坐标中到x、y轴距离其中至少有一个为3的点有,
这些点中与A符合“等距点”的是.
故答案为①E、F;②;
(2)两点为“等距点”,
①若时,则或
解得(舍去)或.
②若时,则
解得或(舍去).
根据“等距点”的定义知,或符合题意.
即k的值是1或2.
22.(1)6,
(2)(ⅰ)7(ⅱ)9
【分析】本题考查用坐标表示位置,掌握题干给定的表示方法,是解题的关键:
(1)根据给定的坐标的的表示方法,进行作答即可;
(2)(ⅰ)由题意,可知,在一条直线上且在点同侧,横坐标之差即为,两点间的距离;
(ⅱ)由题意,可知,在一条直线上,横坐标之差即为,两点间的距离;
【详解】(1)解:∵,
∴,
故答案为:;
(2)(ⅰ)如图,
∵,,
∴三点共线,在点的同侧,
∴;
故答案为:7;
(ⅱ)如图:
由题意,得:,
∴三点共线,且在点的两侧,
∴;
故答案为:9.
23.(1)点A坐标为(-3,0),点B坐标为(0,4);(2)点C坐标为(0,-4);(3)存在,点P坐标为(,0)或(-,0).
【分析】(1)解方程可求出b的值,即可得A、B坐标;
(2)根据A、B坐标可得OA、OB的长,利用三角形面积公式可求出BC的长,根据点C在y轴负半轴可得OC的长,可得C点坐标;
(3)利用三角形面积公式可求出OP的长,分点P在原点左边和右边两种情况,求出OP的坐标即可.
【详解】(1)∵,
∴b=1,
∵,,
∴点A坐标为(-3,0),点B坐标为(0,4).
(2)如图,∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∵△ABC的面积为12,
∴BC·OA=12,即×3×BC=12,
解得:BC=8,
∵点为轴负半轴上一点,
∴OC=BC-OB=8-4=4,
∴点C坐标为(0,-4).
(3)如图,∵的面积等于的面积的一半,△ABC的面积为12,
∴△PBC的面积为6,
∴BC·OP=6,即×8×OP=6,
解得:OP=,
当点P在原点左边时,点P坐标为(-,0),
当点P在原点右边时,点P坐标为(,0),
∴存在一点,使的面积等于的面积的一半,点P坐标为(,0)或(-,0).
【点睛】本题考查坐标与图形的性质及三角形的面积,运用分类讨论的思想是解题关键.
答案第1页,共2页
答案第1页,共2页
