9.5 三角形的中位线 同步练习(无答案)2023-2024学年苏科版数学八年级下册
文档属性
| 名称 | 9.5 三角形的中位线 同步练习(无答案)2023-2024学年苏科版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 21:09:34 | ||
图片预览

文档简介
9.5 三角形的中位线
一.选择题
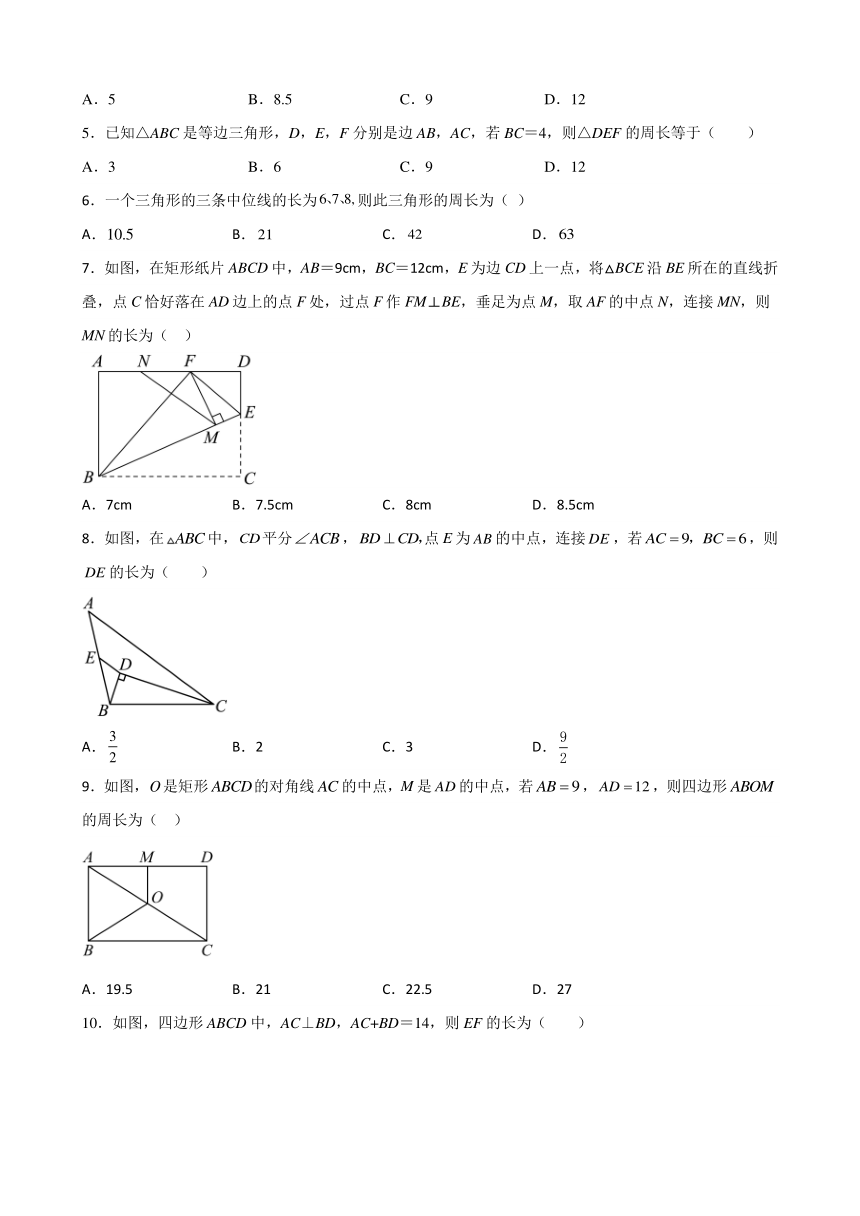
1.如图,D、E分别为△ABC边AC、BC的中点,∠A=60°,则下列判断错误的是( )
A.∠ADE=120° B.AB=12 C.∠CDE=60° D.DC=6
2.如图,在△ABC中,BC=5,E,AC的中点,动点P在射线EF上,∠CBP的平分线交CE于点Q,当CQ=,EP+BP的值为( )
A.10 B.8 C.6 D.5
3.已知在四边形ABCD中,AB=3,CD=5,M,BC的中点,则线段MN的取值范围是( )
A.1<MN<4 B.1<MN≤4 C.2<MN<8 D.2<MN≤8
4.如图,在Rt△ABC中,∠B=90°,AB=12,点D,AC的中点,CF平分Rt△ABC的一个外角∠ACM,则DF的长为( )
A.5 B.8.5 C.9 D.12
5.已知△ABC是等边三角形,D,E,F分别是边AB,AC,若BC=4,则△DEF的周长等于( )
A.3 B.6 C.9 D.12
6.一个三角形的三条中位线的长为则此三角形的周长为( )
A. B. C. D.
7.如图,在矩形纸片ABCD中,AB=9cm,BC=12cm,E为边CD上一点,将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN的长为( )
A.7cm B.7.5cm C.8cm D.8.5cm
8.如图,在中,平分,点E为的中点,连接,若,则的长为( )
A. B.2 C.3 D.
9.如图,是矩形的对角线的中点,M是的中点,若,,则四边形的周长为( )
A.19.5 B.21 C.22.5 D.27
10.如图,四边形ABCD中,AC⊥BD,AC+BD=14,则EF的长为( )
A.5 B.6 C.8 D.10
二.填空题
1.如图,为估计池塘两岸边A、B两点间的距离,在池塘的一侧选取点C,测得DE=15m,则A、B两点间的距离是 .
2.在中,,点N是边上一点,点M为边上的动点,点D、E分别为的中点,则的最小值是 ___________.
3.如图,在中,AC、BD相交于O,E是CD的中点,连接OE,的周长为8,则的周长为______.
4.如图,中,,点,点,、分别为、的中点,则的长度为________.
5.如图,在△ABC中,AB=AC,E,AC的中点,以AC为斜边作Rt△ADC,则下列结论:①CD∥EF;②EF=DF;⑤AB=CD (填序号)
三.解答题
1.如图,在△ABC中,AB=AC,E分别是边AB,AC的中点,点F,G,H分别为BE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
2.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
3.如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)请判断四边形EFGH的形状?并说明为什么.
(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?
(3)在(2)的条件下,若EF=2,求四边形ABCD的面积.
4如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
5.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC)
(2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想
一.选择题
1.如图,D、E分别为△ABC边AC、BC的中点,∠A=60°,则下列判断错误的是( )
A.∠ADE=120° B.AB=12 C.∠CDE=60° D.DC=6
2.如图,在△ABC中,BC=5,E,AC的中点,动点P在射线EF上,∠CBP的平分线交CE于点Q,当CQ=,EP+BP的值为( )
A.10 B.8 C.6 D.5
3.已知在四边形ABCD中,AB=3,CD=5,M,BC的中点,则线段MN的取值范围是( )
A.1<MN<4 B.1<MN≤4 C.2<MN<8 D.2<MN≤8
4.如图,在Rt△ABC中,∠B=90°,AB=12,点D,AC的中点,CF平分Rt△ABC的一个外角∠ACM,则DF的长为( )
A.5 B.8.5 C.9 D.12
5.已知△ABC是等边三角形,D,E,F分别是边AB,AC,若BC=4,则△DEF的周长等于( )
A.3 B.6 C.9 D.12
6.一个三角形的三条中位线的长为则此三角形的周长为( )
A. B. C. D.
7.如图,在矩形纸片ABCD中,AB=9cm,BC=12cm,E为边CD上一点,将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN的长为( )
A.7cm B.7.5cm C.8cm D.8.5cm
8.如图,在中,平分,点E为的中点,连接,若,则的长为( )
A. B.2 C.3 D.
9.如图,是矩形的对角线的中点,M是的中点,若,,则四边形的周长为( )
A.19.5 B.21 C.22.5 D.27
10.如图,四边形ABCD中,AC⊥BD,AC+BD=14,则EF的长为( )
A.5 B.6 C.8 D.10
二.填空题
1.如图,为估计池塘两岸边A、B两点间的距离,在池塘的一侧选取点C,测得DE=15m,则A、B两点间的距离是 .
2.在中,,点N是边上一点,点M为边上的动点,点D、E分别为的中点,则的最小值是 ___________.
3.如图,在中,AC、BD相交于O,E是CD的中点,连接OE,的周长为8,则的周长为______.
4.如图,中,,点,点,、分别为、的中点,则的长度为________.
5.如图,在△ABC中,AB=AC,E,AC的中点,以AC为斜边作Rt△ADC,则下列结论:①CD∥EF;②EF=DF;⑤AB=CD (填序号)
三.解答题
1.如图,在△ABC中,AB=AC,E分别是边AB,AC的中点,点F,G,H分别为BE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
2.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
3.如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)请判断四边形EFGH的形状?并说明为什么.
(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?
(3)在(2)的条件下,若EF=2,求四边形ABCD的面积.
4如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
5.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC)
(2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
