6.2.1排列 课件(共14张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 6.2.1排列 课件(共14张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 925.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 21:23:26 | ||
图片预览





文档简介
(共14张PPT)
第六章 计数原理
6.2.1 排列
2024
授课教师:
授课时间:2024年5月11日
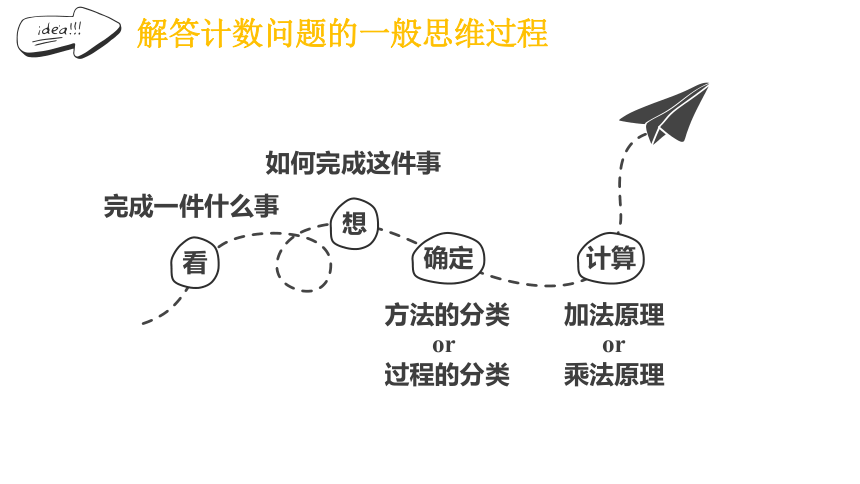
看
确定
计算
完成一件什么事
想
如何完成这件事
方法的分类
or
过程的分类
加法原理
or
乘法原理
解答计数问题的一般思维过程
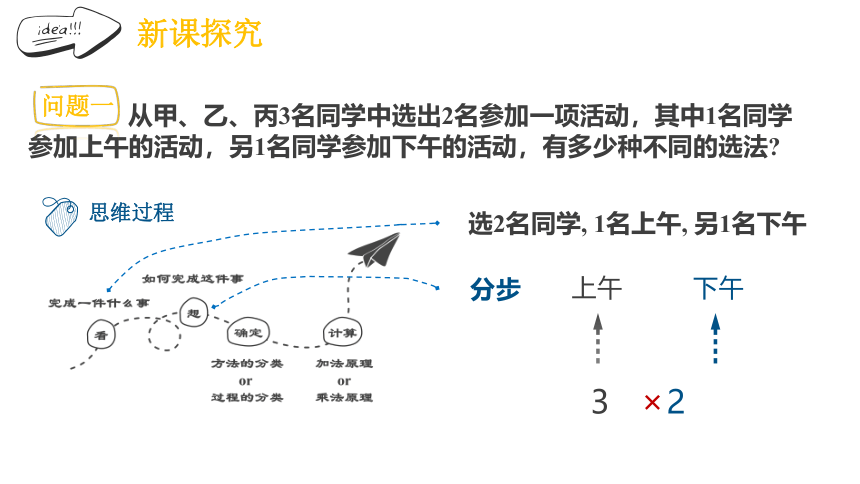
从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法
上午
下午
3 2
×
新课探究
问题一
思维过程
选2名同学, 1名上午, 另1名下午
分步
从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法
问题一
追问一
同学们能列出所有不同的选法吗
3 × 2 = 6
下午
上午
选法
乙 丙 甲 丙 甲 乙
乙
丙乙
上午
下午
甲
丙
乙丙
甲乙
甲丙
乙甲
丙甲
追问二
如果把上面问题中被取出的同学叫元素,那么问题1可以归结为:
从3个不同的元素a、b、c 中任意取出2个,并按上午、下午的顺序排成一列,共有多少种不同的排列方法
从1、2、3、4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题二
任务一
请同学们列出所有不同的三位数.
十位
百位
个位
4 × 3 × 2 = 24
123,124,132,134,142,143,
213,214,231,234,241,243, 312,314,321,324,341,342, 412,413,421,423,431,432.
追问二
如果把上面问题中被取出的数叫元素,那么问题2可以归结为:
从4个不同的元素a、 b 、c 、d中任意取出3个,并按百位、十位、个位的顺序排成一列,共有多少种不同的排列方法
列举:避免重复&遗漏
从3个不同的元素a、b、c 中任意取出2个,并按上午、下午的顺序排成一列,共有多少种不同的排列方法
从4个不同的元素a、 b 、c 、d中任意取出3个,并按百位、十位、个位的顺序排成一列,共有多少种不同的排列方法
从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法
问题一
从1、2、3、4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题二
问题1、问题2的共同点是什么 能否推广到一般
问题三
从3个不同的元素a、b、c 中任意取出2个,并按上午、下午的顺序排成一列,共有多少种不同的排列方法
从4个不同的元素a、 b 、c 、d中任意取出3个,并按百位、十位、个位的顺序排成一列,共有多少种不同的排列方法
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的
顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列。
概念形成
两个基本内容:
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的
顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列。
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的
顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列。
提取元素
按照顺序
元素不能重复
大家思考一下两个排列相同的充要条件是什么
问题四
元素相同,排列顺序相同.
概念辨析
下列问题中哪些是排列问题
(1)10名学生中抽2名学生开会;
(2)10名学生中选2名做正、副组长;
(3)从2、3、5、7、11中任取两个数相乘;
(4)从2、3、5、7、11中任取两个数相除;
(5)从高二4班全体同学中选5人组成课外数学学习小组;
(6)从高二5班全体同学中选5人分别参加校运动会的5个不同运动项目。
判断方法:
(1) 元素无重复性
(2)元素有序性
变换元素的位置,看结果是否发生变化
有:有序
无:无序
例题讲解
某省中学生足球预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛
(1)一张餐桌上有5盘不同的菜,甲乙丙3名同学每人从中各取
一盘菜,共有多少种不同的取法
(2)学校食堂的一个窗口共卖5种菜,甲乙丙3名同学每人从中选1种
共有多少种不同的选法
这两个问题的区别在哪里
问题五
已知集合M={1,2,3,4,5},P(a,b)(a≠b,a,b∈M) 表示平面上的一 点,P可以表示平面上多少个不同的点 并列出这些点。
变式训练
课堂小结
通过这节课的学习,你有哪些收获
试从知识、方法、数学思想等方面谈谈。
作业布置
必做题:课本16页练习1、练习2
选做题:课本16页练习3
巩固练习
4个人A、B、C、D 坐成一排照相有多少种做法 将它们列出来。
有3名男生和2名女生,从中选出3人分别担任语文、数学、
英语学科的课代表,则不同的选法共有多少种?
THANKS
2024
第六章 计数原理
6.2.1 排列
2024
授课教师:
授课时间:2024年5月11日
看
确定
计算
完成一件什么事
想
如何完成这件事
方法的分类
or
过程的分类
加法原理
or
乘法原理
解答计数问题的一般思维过程
从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法
上午
下午
3 2
×
新课探究
问题一
思维过程
选2名同学, 1名上午, 另1名下午
分步
从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法
问题一
追问一
同学们能列出所有不同的选法吗
3 × 2 = 6
下午
上午
选法
乙 丙 甲 丙 甲 乙
乙
丙乙
上午
下午
甲
丙
乙丙
甲乙
甲丙
乙甲
丙甲
追问二
如果把上面问题中被取出的同学叫元素,那么问题1可以归结为:
从3个不同的元素a、b、c 中任意取出2个,并按上午、下午的顺序排成一列,共有多少种不同的排列方法
从1、2、3、4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题二
任务一
请同学们列出所有不同的三位数.
十位
百位
个位
4 × 3 × 2 = 24
123,124,132,134,142,143,
213,214,231,234,241,243, 312,314,321,324,341,342, 412,413,421,423,431,432.
追问二
如果把上面问题中被取出的数叫元素,那么问题2可以归结为:
从4个不同的元素a、 b 、c 、d中任意取出3个,并按百位、十位、个位的顺序排成一列,共有多少种不同的排列方法
列举:避免重复&遗漏
从3个不同的元素a、b、c 中任意取出2个,并按上午、下午的顺序排成一列,共有多少种不同的排列方法
从4个不同的元素a、 b 、c 、d中任意取出3个,并按百位、十位、个位的顺序排成一列,共有多少种不同的排列方法
从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法
问题一
从1、2、3、4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数
问题二
问题1、问题2的共同点是什么 能否推广到一般
问题三
从3个不同的元素a、b、c 中任意取出2个,并按上午、下午的顺序排成一列,共有多少种不同的排列方法
从4个不同的元素a、 b 、c 、d中任意取出3个,并按百位、十位、个位的顺序排成一列,共有多少种不同的排列方法
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的
顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列。
概念形成
两个基本内容:
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的
顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列。
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的
顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列。
提取元素
按照顺序
元素不能重复
大家思考一下两个排列相同的充要条件是什么
问题四
元素相同,排列顺序相同.
概念辨析
下列问题中哪些是排列问题
(1)10名学生中抽2名学生开会;
(2)10名学生中选2名做正、副组长;
(3)从2、3、5、7、11中任取两个数相乘;
(4)从2、3、5、7、11中任取两个数相除;
(5)从高二4班全体同学中选5人组成课外数学学习小组;
(6)从高二5班全体同学中选5人分别参加校运动会的5个不同运动项目。
判断方法:
(1) 元素无重复性
(2)元素有序性
变换元素的位置,看结果是否发生变化
有:有序
无:无序
例题讲解
某省中学生足球预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛
(1)一张餐桌上有5盘不同的菜,甲乙丙3名同学每人从中各取
一盘菜,共有多少种不同的取法
(2)学校食堂的一个窗口共卖5种菜,甲乙丙3名同学每人从中选1种
共有多少种不同的选法
这两个问题的区别在哪里
问题五
已知集合M={1,2,3,4,5},P(a,b)(a≠b,a,b∈M) 表示平面上的一 点,P可以表示平面上多少个不同的点 并列出这些点。
变式训练
课堂小结
通过这节课的学习,你有哪些收获
试从知识、方法、数学思想等方面谈谈。
作业布置
必做题:课本16页练习1、练习2
选做题:课本16页练习3
巩固练习
4个人A、B、C、D 坐成一排照相有多少种做法 将它们列出来。
有3名男生和2名女生,从中选出3人分别担任语文、数学、
英语学科的课代表,则不同的选法共有多少种?
THANKS
2024
