6.3.2 二项式系数的性质 课件(共15张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 6.3.2 二项式系数的性质 课件(共15张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 21:25:36 | ||
图片预览






文档简介
(共15张PPT)
第六章 计 数 原 理
6.3.2 二项式系数的性质
延时符
授课人: 日期:2024年5月12日
学习目标
能记住二项式系数的性质,并能解决相关问题.
会用“赋值法”求展开式系数的和.
数学抽象、数学运算、数学直观
复习巩固
注 意:
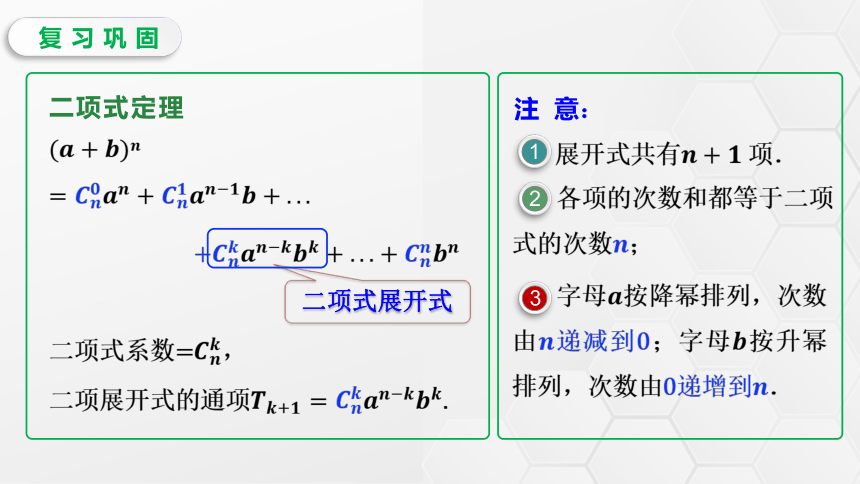
二项式定理
二项式展开式
二项式系数=,
二项展开式的通项.
展开式共有 项.
1
各项的次数和都等于二项式的次数;
2
字母按降幂排列,次数由递减到0;字母按升幂排列,次数由0递增到.
3
新知导入
4
【探究】 用计算工具计算的展开式的二项式系数,并填入下表中.
通过计算,填表,你发现了什么规律?
的展开式的二项式系数
2
3
4
5
6
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
二项式系数
新课知识
5
2
系数呈对称分布;与首末两端“等距离”的两个系数相等;
3
同一行中,系数先增后减,两端的系数小,中间的系数大.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
设表中任一不为1的数为,那么它肩上的
个数分别为和
在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.
4
1
每行两端的数都是1;
新课知识
6
对于 展开式的二项式系数
从函数角度看,可看成是以为自变量的函数,其定义域是
从函数角度分析二项式系数
例如,当时,函数 的图象是右图中的7个孤立点.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
函数,的图像是什么?
个孤立的点
新课知识
7
与首末两端“等距离”的两个二项式系数相等.
事实上,这一性质可直接由公式 得到.
图象的对称轴为
对称性
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
新课知识
8
当n为奇数时,中间两项的二项式系数和相等,且同时取得最大值;
二项式系数的前半部分是递增的,后半部分是递减的.
在中间项取得最大值.
当n为偶数时,中间一项的二项式系数取得最大值;
1 6 15 20 15 6 1
增减性与最大值
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
例题精讲
9
这就是说,的展开式的各二项式系数的和等于.
各二项式系数的和
已知,
令,得.
赋值法
例题精讲
10
【例3】求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
【解】在展开式 中,
令,,
即.
即在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
因此,,
赋值法
课堂练习
11
课堂练习
12
课堂小结
13
二项式系数的性质
与首末两端“等距离”的两个二项式系数相等.
图象的对称轴为
对称性
增减性与最大值
当n为奇数时,中间两项的二项式系数和相等,且同时取得最大值;
二项式系数的前半部分是递增,后半部递减,在中间项取得最大值.
当n为偶数时,中间一项的二项式系数取得最大值;
各二项式系数的和
.
本课作业
必做 二
必做 一
选做 一
教材 35 页
习题 7~11
三维 49页
课后 1~5
2
01
02
03
微信: 手机:
感谢您的观看
授课人:梅河口市朝鲜族中学
第六章 计 数 原 理
6.3.2 二项式系数的性质
延时符
授课人: 日期:2024年5月12日
学习目标
能记住二项式系数的性质,并能解决相关问题.
会用“赋值法”求展开式系数的和.
数学抽象、数学运算、数学直观
复习巩固
注 意:
二项式定理
二项式展开式
二项式系数=,
二项展开式的通项.
展开式共有 项.
1
各项的次数和都等于二项式的次数;
2
字母按降幂排列,次数由递减到0;字母按升幂排列,次数由0递增到.
3
新知导入
4
【探究】 用计算工具计算的展开式的二项式系数,并填入下表中.
通过计算,填表,你发现了什么规律?
的展开式的二项式系数
2
3
4
5
6
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
二项式系数
新课知识
5
2
系数呈对称分布;与首末两端“等距离”的两个系数相等;
3
同一行中,系数先增后减,两端的系数小,中间的系数大.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
设表中任一不为1的数为,那么它肩上的
个数分别为和
在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.
4
1
每行两端的数都是1;
新课知识
6
对于 展开式的二项式系数
从函数角度看,可看成是以为自变量的函数,其定义域是
从函数角度分析二项式系数
例如,当时,函数 的图象是右图中的7个孤立点.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
函数,的图像是什么?
个孤立的点
新课知识
7
与首末两端“等距离”的两个二项式系数相等.
事实上,这一性质可直接由公式 得到.
图象的对称轴为
对称性
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
新课知识
8
当n为奇数时,中间两项的二项式系数和相等,且同时取得最大值;
二项式系数的前半部分是递增的,后半部分是递减的.
在中间项取得最大值.
当n为偶数时,中间一项的二项式系数取得最大值;
1 6 15 20 15 6 1
增减性与最大值
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
例题精讲
9
这就是说,的展开式的各二项式系数的和等于.
各二项式系数的和
已知,
令,得.
赋值法
例题精讲
10
【例3】求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
【解】在展开式 中,
令,,
即.
即在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
因此,,
赋值法
课堂练习
11
课堂练习
12
课堂小结
13
二项式系数的性质
与首末两端“等距离”的两个二项式系数相等.
图象的对称轴为
对称性
增减性与最大值
当n为奇数时,中间两项的二项式系数和相等,且同时取得最大值;
二项式系数的前半部分是递增,后半部递减,在中间项取得最大值.
当n为偶数时,中间一项的二项式系数取得最大值;
各二项式系数的和
.
本课作业
必做 二
必做 一
选做 一
教材 35 页
习题 7~11
三维 49页
课后 1~5
2
01
02
03
微信: 手机:
感谢您的观看
授课人:梅河口市朝鲜族中学
