2.3 匀变速直线运动的位移与时间的关系(原卷版) (人教版2019必修第一册)高中物理同步讲义练习
文档属性
| 名称 | 2.3 匀变速直线运动的位移与时间的关系(原卷版) (人教版2019必修第一册)高中物理同步讲义练习 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-05-13 22:10:19 | ||
图片预览




文档简介
2.3 匀变速直线运动的位移与时间的关系
(
学习目标
)
课程标准 学习目标
1.了解速度时间图像围成的面积为相应时间内的位移。能利用速度时间图像得出匀变速直线运动的位移与时间关系式,进一步体会用图像分析物体运动规律的研究方法。 2.能推导出匀变速直线运动的速度与位移关系式,体会科学推理的逻辑严密性。 3.能在实际问题情境中使用匀变速直线运动的位移公式解决问题,体会物理知识的实际应用价值。, 1.知道v t图像中“面积”与位移的对应关系. 2.理解位移与时间的关系式的意义. 3.掌握三个平均速度公式及其适用条件,会用平均速度求解相关问题. 4.会推导位移差公式Δx=aT2,会用它解决相关问题.
(
0
2
预习导学
)
课前研读课本,梳理基础知识:
一、匀速直线运动的位移
1.位移公式:
2.v t图像特点
(1)平行于 的直线.
(2)位移Δx就对应着那段图像与两个坐标轴间所围成的矩形(即图中阴影区域)的 .
二、匀变速直线运动的位移
1.位移在v t图像中的表示
(1)微元法推导
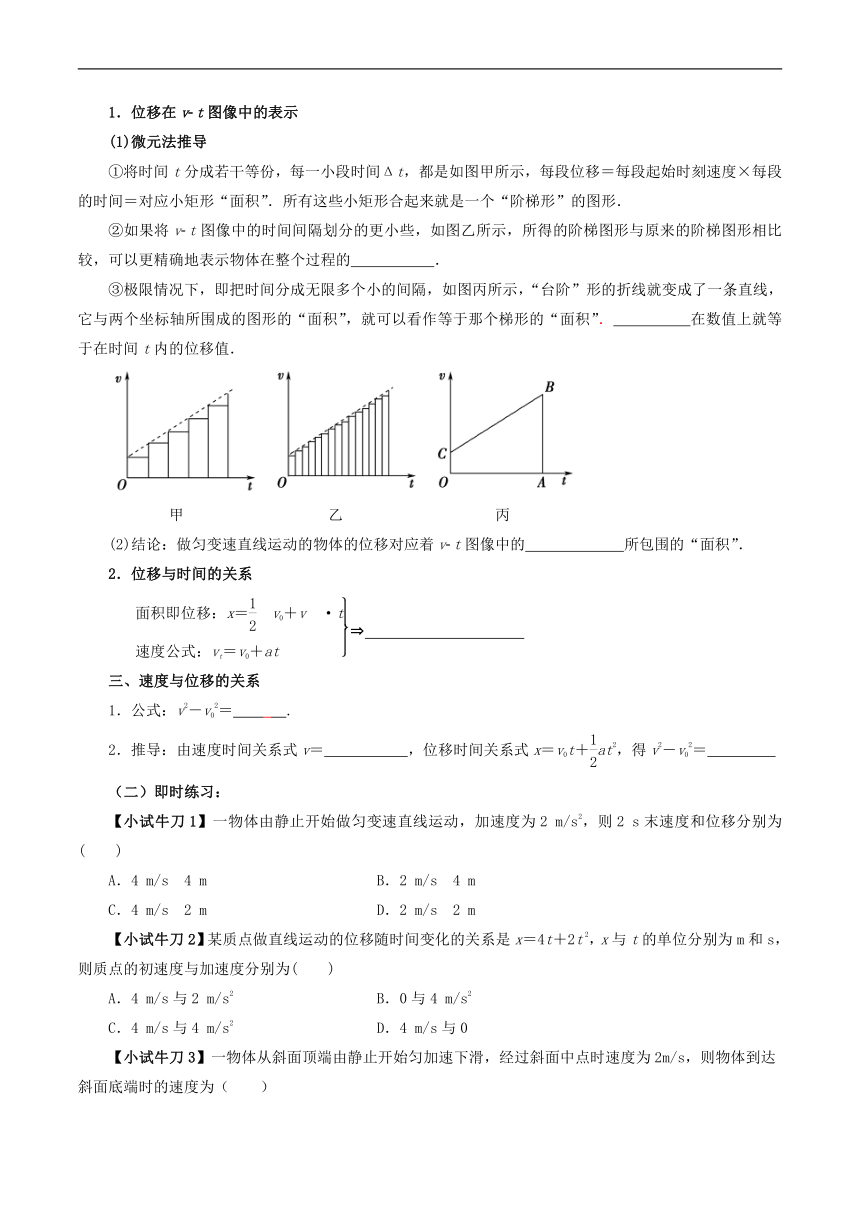
①将时间t分成若干等份,每一小段时间Δt,都是如图甲所示,每段位移=每段起始时刻速度×每段的时间=对应小矩形“面积”.所有这些小矩形合起来就是一个“阶梯形”的图形.
②如果将v t图像中的时间间隔划分的更小些,如图乙所示,所得的阶梯图形与原来的阶梯图形相比较,可以更精确地表示物体在整个过程的 .
③极限情况下,即把时间分成无限多个小的间隔,如图丙所示,“台阶”形的折线就变成了一条直线,它与两个坐标轴所围成的图形的“面积”,就可以看作等于那个梯形的“面积”. 在数值上就等于在时间t内的位移值.
甲 乙 丙
(2)结论:做匀变速直线运动的物体的位移对应着v t图像中的 所包围的“面积”.
2.位移与时间的关系
三、速度与位移的关系
1.公式:v2-v02= .
2.推导:由速度时间关系式v= ,位移时间关系式x=v0t+at2,得v2-v02=
(二)即时练习:
【小试牛刀1】一物体由静止开始做匀变速直线运动,加速度为2 m/s2,则2 s末速度和位移分别为( )
A.4 m/s 4 m B.2 m/s 4 m
C.4 m/s 2 m D.2 m/s 2 m
【小试牛刀2】某质点做直线运动的位移随时间变化的关系是x=4t+2t 2,x与t的单位分别为m和s,则质点的初速度与加速度分别为( )
A.4 m/s与2 m/s2 B.0与4 m/s2
C.4 m/s与4 m/s2 D.4 m/s与0
【小试牛刀3】一物体从斜面顶端由静止开始匀加速下滑,经过斜面中点时速度为2m/s,则物体到达斜面底端时的速度为( )
A. B.3m/s C.4m/s D.6m/s
(
0
3
探究提升
)
【问题探究1】匀变速直线运动的位移
1.公式的适用条件:位移公式x=v0t+at2只适用于匀变速直线运动.
2.公式的矢量性:公式x=v0t+at2为矢量公式,其中x、v0、a都是矢量,应用时必须选取统一的正方向,一般选v0的方向为正方向.通常有以下几种情况:
运动情况 取值
若物体做匀加速直线运动 a与v0同向,a取正值(v0方向为正方向)
若物体做匀减速直线运动 a与v0反向,a取负值(v0方向为正方向)
若位移的计算结果为正值 说明位移的方向与规定的正方向相同
若位移的计算结果为负值 说明位移的方向与规定的正方向相反
3.公式的两种特殊形式
(1)当a=0时,x=v0t(匀速直线运动).
(2)当v0=0时,x=at2(由静止开始的匀加速直线运动).
【典型例题1】一辆汽车正在平直的公路上以72 km/h的速度行驶,司机看见红色信号灯便立即踩下制动器,此后,汽车开始做匀减速直线运动.设汽车减速过程的加速度大小为5 m/s2,求:
(1)开始制动后,前2 s内汽车行驶的距离;
(2)开始制动后,前5 s内汽车行驶的距离.
【典型例题2】如图所示,某商场在4.56m高的楼层间设有自动扶梯,自动扶梯匀速前进的速度是0.76m/s,与水平面的夹角是30°。则顾客从该自动扶梯的起点(顾客站立不动)乘电梯上楼所用的时间是( )
A.3s B.6s C.12s D.24s
【对点训练1】物体做匀减速直线运动,初速度为10 m/s,加速度大小为1 m/s2,则物体在停止运动前1 s内的平均速度为 ( )
A.5.5 m/s B.5 m/s
C.1 m/s D.0.5 m/s
【对点训练2】在平直公路上,一辆汽车以 2m/s2 的加速度从静止开始做匀加速直线运动,经过 4s 汽车行驶的路程是( )
A.6m B.8m C.12m D.16m
【问题探究2】速度和位移的关系式
1.速度和位移的关系式的推导:
⑴ 由于,又有,即,
则由,推出。
⑵ 图象证明:
第一步:在图中一个以轴为底的直角三角形的面积为
第二步:对于一个有一定初速度的匀加速直线运动
2.匀变速直线运动的基本关系式及推论
(1)速度与时间关系式∶v=v0+at①,题目中不涉及位移x,可直接选用。
(2)位移与时间关系式∶x=v0t+at2②,题目中不涉及末速度v,方便使用。
(3)速度与位移关系式∶v2-v02=2ax③,题目中不涉及时间t,可直接选用。
(4)平均速度求位移公式∶x =④,题目中不涉及加速度a,方便使用。
(5)纸带数据常用推论公式∶△x=aT2⑤,未涉及物理量v。
【典型例题3】根据我国机动车运行安全的技术标准,一辆满载的大型汽车,如行驶速度为 30 km/h,制动距离必须在8.0 m 以内。当它的行驶速度为 60 km/h 时,制动距离须控制在( )以内。
A.8m B.16m C.32m D.64m
【典型例题4】汽车以的速度开始刹车,刹车中加速度大小为,关于汽车的运动情况,下列说法正确的是( )
A.刹车后6s末的速度为2m/s
B.刹车后6s内的位移为25m
C.刹车后6s内的位移为24m
D.停止前第3s、第2s、最后1s的位移之比为5:3:1
【对点训练3】汽车在平直的公路上匀速行驶,发现前方有险情后紧急刹车,刹车后经过2s速度减半,再滑行15m速度减为零,刹车过程可以看成匀减速直线运动,则汽车匀速行驶时的速度大小为( )
A.25m/s B.28m/s C.30m/s D.32m/s
【对点训练4】飞机在跑道上滑行,离地起飞时的速度是,若飞机滑行时加速度大小为,则飞机从开始滑行至起飞需时间______s,起飞的跑道长至少为______m。
【问题探究3】两个重要推论
1.平均速度:做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的一半。即==vt/2=
2位移差公式
(1)匀变速直线运动中,在连续相等的时间T内的位移之差为一恒定值,即Δx=x2-x1=aT2.
(2)应用:a.判断物体是否做匀变速直线运动:
如果Δx=x2-x1=x3-x2=…=xn-xn-1=aT2成立,则a为一恒量,说明物体做匀变速直线运动.
b.求加速度:利用Δx=aT2,可求得a=.
3.位移中点的瞬时速度公式:做匀速直线运动的物体,在某段位移中点位置的瞬时速度.
【典型例题5】如图所示,物体从O点开始做初速度不为零的匀加速直线运动,在第一个时间T内通过位移为s1到达A点,紧接着在第二个时间T内通过位移为s2到达B点,则以下判断正确的是
A.物体运动的加速度为
B.物体运动的加速度为
C.物体在A点的速度大小为
D.物体在B点的速度大小为
【典型例题6】小球在光滑斜面上,从点静止开始下滑,通过、、各段所用时间均为。则( )
A.与位移差等于与位移差
B.通过、段的位移之比为
C.通过、点的速度之比可能为
D.通过点的瞬时速度等于通过段的平均速度
【对点训练5】做匀加速直线运动的质点,在第内和前内的平均速度之差是,则此质点运动的加速度大小为( )
A. B. C. D.
【对点训练6】从斜面上某一位置每隔0.1s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个小球后,对在斜面上滚动的小球拍下如图所示的照片(照片与实际大小相同),测得x=15cm,x=20cm.试问:
(1)小球的加速度的大小;
(2)拍摄时小球在B点时的速度的大小;
(3)A点的上方滚动的小球还有几个。
【问题探究4】解决匀变速直线运动问题的基本思路
1、→→→→
注意:x、v0、v、a均为矢量,所以解题时需要确定正方向,一般以v0的方向为正方向.
2.匀变速直线运动公式的选用
一般问题用两个基本公式可以解决,以下特殊情况下用导出公式会提高解题的速度和准确率;
(1)不涉及时间,选择v2-v02=2ax;
(2)不涉及加速度,用平均速度公式,比如纸带问题中运用==求瞬时速度;
(3)处理纸带问题时用Δx=x2-x1=aT2,xm-xn=(m-n)aT2求加速度.
3.逆向思维法:对于末速度为零的匀减速运动,采用逆向思维法,倒过来看成初速度为零的匀加速直线运动.
4.图象法:借助v-t图象(斜率、面积)分析运动过程.
v-t图线与t轴所围“面积”表示这段时间内物体的位移:t轴上方的“面积”表示位移沿正方向,t轴下方的“面积”表示位移沿负方向,如果上方与下方的“面积”大小相等,说明物体恰好回到出发点.
【典型例题7】假设某次深海探测活动中,“蛟龙号”完成海底科考任务后竖直上浮,从上浮速度为v时开始匀减速并计时,经过时间t,“蛟龙号”上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0A.vt0(1-) B. C. D.
【典型例题8】航天飞机在平直的跑道上降落,其减速过程可以简化为两个匀减速直线运动.航天飞机以水平速度v0=100 m/s着陆后,立即打开减速阻力伞,以大小为a1=4 m/s2的加速度做匀减速直线运动,一段时间后阻力伞脱离,航天飞机以大小为a2=2.5 m/s2的加速度做匀减速直线运动直至停下.已知两个匀减速直线运动滑行的总位移x=1 370 m.求:
(1)第二个减速阶段航天飞机运动的初速度大小;
(2)航天飞机降落后滑行的总时间.
【对点训练7】航空母舰是大规模战争的重要武器,灵活起降的飞机是它的主要攻击力之一。民航客机起飞时要在2.5min内使飞机从静止加速到44m/s;而舰载飞机借助于助推装置,在2s内就可把飞机从静止加速到82.5m/s而起飞,设飞机起飞时在跑道上做匀加速直线运动,则供客机起飞的跑道长度约是航空母舰的甲板跑道长度的( )
A.40倍 B.80倍 C.400倍 D.800倍
(
0
4
体系构建
)
(
0
5
记忆清单
)
1.对位移时间关系式x=v0t+at2的理解
(1)适用条件:位移公式只适用于匀变速直线运动.
(2)矢量性:公式中x、v0、a都是矢量,应用时必须选取正方向.一般选v0的方向为正方向.
①匀加速直线运动中,a与v0同向,a取正值;匀减速直线运动中,a与v0反向,a取负值.
②若位移的计算结果为正值,说明位移方向与规定的正方向相同;若位移的计算结果为负值,说明位移方向与规定的正方向相反.
(3)两种特殊形式
①当v0=0时,x=at2,即由静止开始的匀加速直线运动的位移公式,位移x与t2成正比.
②当a=0时,x=v0t,即匀速直线运动的位移公式.
2.对公式v2-v02=2ax的理解
(1)v2-v02=2ax为矢量式,适用于匀变速直线运动,x、v0、v、a都是矢量,应用时必须选取统一的正方向,一般选初速度 v0的方向为正方向。
①匀加速直线运动,a取正值;匀减速直线运动,a取负值。
②位移与正方向相同,x取正值;位移与正方向相反,x取负值。
(2)特殊情况∶当v0=0时,公式简化为v2=2ax(物体做初速度为零的匀加速直线运动);当v=0时,公式简化为-v02=2ax(物体做匀减速直线运动直到静止),也可以视为从静止开始、末速度为v0的反向的匀加速直线运动。
(
0
6
0
1
强化训练
)
1.在平直公路上,一辆汽车以 2m/s2 的加速度从静止开始做匀加速直线运动,经过 4s 汽车行驶的路程是( )
A.6m B.8m C.12m D.16m
2.飞机着陆后匀减速滑行,它滑行的初速度是60m/s,加速度的大小是3m/s2,飞机着陆后滑行距离为( )
A.1170m B.600m C.180m D.20m
3.做匀加速直线运动的物体位移随时间变化的函数关系是,则它的初速度是( )
A.0 B. C. D.
4.一辆摩托车在平直的公路上匀加速行驶,经过路旁两相邻电线杆时的速度分别是5m/s和15m/s,已知相邻两电线杆之间的距离是20m。则摩托车的加速度是( )
A.5 m/s2 B.0.5m/s2 C.10 m/s2 D.2.5 m/s2
5.一质点做直线运动的图像如图所示,由图像可知( )
A.质点沿x轴正方向做匀速运动 B.质点沿x轴负方向做匀速运动
C.时,质点的速度是5m/s D.时,质点的速度是
6.蓝牙小音箱可以在一定距离内与手机等设备实现连接,某型号的蓝牙音箱无线连接的有效距离是。在两条平行且靠近的直轨道上,分别放置智能小车A、B,两车分别携带该型号音箱和手机。某时刻两车相距同时开始相向而行,速度大小随时间变化图像均如图所示。则手机与音箱从相互连接到断开连接持续的时间为( )
A. B. C. D.
7.如图是实验中得到的一条纸带,A、B、C、D、E、F、G为7个相邻的计数点,相邻的两个计数点之间还有四个点未画出。量出相邻的计数点之间的距离分别为:SAB=4.20cm、SBC=4.65cm、SCD=5.10cm、SDE=5.54cm、SEF=6.00cm、SFG=6.46cm,已知打点计时器的工作周期为0.02s,则小车的加速度a=( )m/s2。(结果保留2位有效数字)
A.0.45 B.45 C.0.41 D.41
8.冰壶是冬奥会的一个竞赛项目。如图为我国运动员在北京冬奥会比赛中投掷冰壶的情形,冰壶以某一初速度被投出后做匀减速直线运动,用时停止,已知停止运动前最后内位移大小为,则冰壶的初速度大小为( )
A. B. C. D.
9.从静止开始做匀加速直线运动的物体,通过前一半位移和后一半位移所用时间的比值为( )
A. B.
C. D.
10.做匀加速直线运动的物体,通过A、B两点的速度分别为v和3v,则该物体( )
A.通过A、B中点时的速度为
B.通过A、B中点时的速度为2v
C.由A到B运动一半时间时的速度为v
D.由A到B运动一半时间时的速度为2v
11.北京时间2022年11月20日晩上23:00时,第22届世界杯在卡塔尔正式开幕,图为一个足球被踢出后每隔0.1s拍下的频闪照片,,,,,由此可以判定( )
A.足球做匀变速直线运动
B.足球的加速度大小为
C.足球的初速度大小
D.整个过程中足球的平均速度大小为8m/s
12.歼-20隐形战斗机首架技术验证机于2011年1月11日进行首次升空飞行测试,距今刚好十周年。已知某次训练中,歼-20着陆后经过4.5s停下来,若这个过程可看作是匀减速直线运动,则歼-20着陆后的第1s和第2s位移大小之比为( )
A.4:3 B.2:1 C.5:3 D.9:7
13.据了解,CR300AF型复兴号动车组是拥有完全自主国产研发的中国标准动车组体系中的新车型。该车型设计时速为300千米每小时,外观呈淡蓝色,除此之外复兴号动车组全车覆盖免费wifi,且每两个座椅有一个插座。假设一列复兴号动车进站时从某时刻起做匀减速直线运动,分别用时3s、2s、1s连续通过三段位移后停下,则这三段位移的平均速度之比是 ( )
A.9:4:1 B.27:8:1 C.5:3:1 D.3:2:1
14.如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是2L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )
A. B. C. D.v1
15.如图所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18 m。该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5 m/s2。此路段允许行驶的最大速度为12.5 m/s。下列说法中正确的有( )
A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线
B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速
C.如果立即做匀减速运动,在绿灯熄灭前汽车可能通过停车线
D.如果距停车线5 m处减速,汽车能停在停车线处
16.某一学习小组的同学想通过打点计时器在纸带上打出的点迹来探究小车速度随时间变化的规律,实验装置如图所示。
(1)常见的打点计时器有两种:________和_______,它们使用的都是_______电源(填“直流”或“交流”),当电源频率为50Hz时,每隔______s打一个点。
(2)关于本实验,下列说法正确的是_______。
A.释放纸带的同时,接通电源
B.先接通电源打点,后释放纸带运动
C.先释放纸带运动,后接通电源打点
D.纸带上的点迹越密集,说明纸带运动的速度越小
(3)要测量小车的速度。除打点计时器(含所用电源、纸带、墨粉纸盘)外还必须使用的测量工具是_______。
(4)该小组在规范操作下得到一条点迹清晰的纸带如图所示,在纸带上依次选出7个计数点,分别标上O、A、B、C、D、E和F,每相邻的两个计数点间还有四个点未画出,打点计时器所用电源的频率是50Hz。
①每相邻两计数点的时间间隔为________s,如果测得C、D两点间距x4=2.70cm,
D、E两点间距x5=2.90cm,则打D点时小车的速度vD=________m/s(结果保留3位有效数字)。
②该同学分别算出其他各点的速度:vA=0.220m/s,vB=0.241m/s,vC=0.258m/s,vE=0.300m/s,请在如图所示的坐标系中作出小车运动的v-t图像_______,并求出小车的加速度= _______ m/s2(结果保留3位有效数字)。
17.在高速公路上,有时会发生“追尾”事故——后面的汽车撞上前面的汽车。某段平直高速公路的最高车速限制为108 km/h,设某人驾车正以最高时速沿该高速公路匀速行驶,该车刹车时产生的加速度大小为5 m/s2,该人的反应时间(从意识到应该停车到操作刹车的时间)为0.5 s。求行驶时的安全车距至少为多少?
18.随着我国高速公路的发展,越来越多的人选择开车出行,这也造成了高速路的拥堵,为此开发了电子不停车收费系统ETC,汽车分别通过ETC通道和人工收费通道的流程如图所示,假设汽车以v1=72 km/h的速度沿直线朝着收费站正常行驶,如果过ETC通道,需要在汽车运动到通道口时速度恰好减为v2=4 m/s,然后匀速通过总长度为d=16 m的通道,接着再匀加速至v1后正常行驶;如果过人工收费通道,需要恰好在中心线处匀减速至零,经过t0=20 s的时间缴费成功后,再启动汽车匀加速至v1后正常行驶,设汽车加速和减速过程中的加速度大小均为a=1 m/s2,求:
(1)汽车过ETC通道时,从开始减速到恢复正常行驶过程中的位移x;
(2)汽车通过ETC通道比通过人工收费通道节约的时间Δt。
(
学习目标
)
课程标准 学习目标
1.了解速度时间图像围成的面积为相应时间内的位移。能利用速度时间图像得出匀变速直线运动的位移与时间关系式,进一步体会用图像分析物体运动规律的研究方法。 2.能推导出匀变速直线运动的速度与位移关系式,体会科学推理的逻辑严密性。 3.能在实际问题情境中使用匀变速直线运动的位移公式解决问题,体会物理知识的实际应用价值。, 1.知道v t图像中“面积”与位移的对应关系. 2.理解位移与时间的关系式的意义. 3.掌握三个平均速度公式及其适用条件,会用平均速度求解相关问题. 4.会推导位移差公式Δx=aT2,会用它解决相关问题.
(
0
2
预习导学
)
课前研读课本,梳理基础知识:
一、匀速直线运动的位移
1.位移公式:
2.v t图像特点
(1)平行于 的直线.
(2)位移Δx就对应着那段图像与两个坐标轴间所围成的矩形(即图中阴影区域)的 .
二、匀变速直线运动的位移
1.位移在v t图像中的表示
(1)微元法推导
①将时间t分成若干等份,每一小段时间Δt,都是如图甲所示,每段位移=每段起始时刻速度×每段的时间=对应小矩形“面积”.所有这些小矩形合起来就是一个“阶梯形”的图形.
②如果将v t图像中的时间间隔划分的更小些,如图乙所示,所得的阶梯图形与原来的阶梯图形相比较,可以更精确地表示物体在整个过程的 .
③极限情况下,即把时间分成无限多个小的间隔,如图丙所示,“台阶”形的折线就变成了一条直线,它与两个坐标轴所围成的图形的“面积”,就可以看作等于那个梯形的“面积”. 在数值上就等于在时间t内的位移值.
甲 乙 丙
(2)结论:做匀变速直线运动的物体的位移对应着v t图像中的 所包围的“面积”.
2.位移与时间的关系
三、速度与位移的关系
1.公式:v2-v02= .
2.推导:由速度时间关系式v= ,位移时间关系式x=v0t+at2,得v2-v02=
(二)即时练习:
【小试牛刀1】一物体由静止开始做匀变速直线运动,加速度为2 m/s2,则2 s末速度和位移分别为( )
A.4 m/s 4 m B.2 m/s 4 m
C.4 m/s 2 m D.2 m/s 2 m
【小试牛刀2】某质点做直线运动的位移随时间变化的关系是x=4t+2t 2,x与t的单位分别为m和s,则质点的初速度与加速度分别为( )
A.4 m/s与2 m/s2 B.0与4 m/s2
C.4 m/s与4 m/s2 D.4 m/s与0
【小试牛刀3】一物体从斜面顶端由静止开始匀加速下滑,经过斜面中点时速度为2m/s,则物体到达斜面底端时的速度为( )
A. B.3m/s C.4m/s D.6m/s
(
0
3
探究提升
)
【问题探究1】匀变速直线运动的位移
1.公式的适用条件:位移公式x=v0t+at2只适用于匀变速直线运动.
2.公式的矢量性:公式x=v0t+at2为矢量公式,其中x、v0、a都是矢量,应用时必须选取统一的正方向,一般选v0的方向为正方向.通常有以下几种情况:
运动情况 取值
若物体做匀加速直线运动 a与v0同向,a取正值(v0方向为正方向)
若物体做匀减速直线运动 a与v0反向,a取负值(v0方向为正方向)
若位移的计算结果为正值 说明位移的方向与规定的正方向相同
若位移的计算结果为负值 说明位移的方向与规定的正方向相反
3.公式的两种特殊形式
(1)当a=0时,x=v0t(匀速直线运动).
(2)当v0=0时,x=at2(由静止开始的匀加速直线运动).
【典型例题1】一辆汽车正在平直的公路上以72 km/h的速度行驶,司机看见红色信号灯便立即踩下制动器,此后,汽车开始做匀减速直线运动.设汽车减速过程的加速度大小为5 m/s2,求:
(1)开始制动后,前2 s内汽车行驶的距离;
(2)开始制动后,前5 s内汽车行驶的距离.
【典型例题2】如图所示,某商场在4.56m高的楼层间设有自动扶梯,自动扶梯匀速前进的速度是0.76m/s,与水平面的夹角是30°。则顾客从该自动扶梯的起点(顾客站立不动)乘电梯上楼所用的时间是( )
A.3s B.6s C.12s D.24s
【对点训练1】物体做匀减速直线运动,初速度为10 m/s,加速度大小为1 m/s2,则物体在停止运动前1 s内的平均速度为 ( )
A.5.5 m/s B.5 m/s
C.1 m/s D.0.5 m/s
【对点训练2】在平直公路上,一辆汽车以 2m/s2 的加速度从静止开始做匀加速直线运动,经过 4s 汽车行驶的路程是( )
A.6m B.8m C.12m D.16m
【问题探究2】速度和位移的关系式
1.速度和位移的关系式的推导:
⑴ 由于,又有,即,
则由,推出。
⑵ 图象证明:
第一步:在图中一个以轴为底的直角三角形的面积为
第二步:对于一个有一定初速度的匀加速直线运动
2.匀变速直线运动的基本关系式及推论
(1)速度与时间关系式∶v=v0+at①,题目中不涉及位移x,可直接选用。
(2)位移与时间关系式∶x=v0t+at2②,题目中不涉及末速度v,方便使用。
(3)速度与位移关系式∶v2-v02=2ax③,题目中不涉及时间t,可直接选用。
(4)平均速度求位移公式∶x =④,题目中不涉及加速度a,方便使用。
(5)纸带数据常用推论公式∶△x=aT2⑤,未涉及物理量v。
【典型例题3】根据我国机动车运行安全的技术标准,一辆满载的大型汽车,如行驶速度为 30 km/h,制动距离必须在8.0 m 以内。当它的行驶速度为 60 km/h 时,制动距离须控制在( )以内。
A.8m B.16m C.32m D.64m
【典型例题4】汽车以的速度开始刹车,刹车中加速度大小为,关于汽车的运动情况,下列说法正确的是( )
A.刹车后6s末的速度为2m/s
B.刹车后6s内的位移为25m
C.刹车后6s内的位移为24m
D.停止前第3s、第2s、最后1s的位移之比为5:3:1
【对点训练3】汽车在平直的公路上匀速行驶,发现前方有险情后紧急刹车,刹车后经过2s速度减半,再滑行15m速度减为零,刹车过程可以看成匀减速直线运动,则汽车匀速行驶时的速度大小为( )
A.25m/s B.28m/s C.30m/s D.32m/s
【对点训练4】飞机在跑道上滑行,离地起飞时的速度是,若飞机滑行时加速度大小为,则飞机从开始滑行至起飞需时间______s,起飞的跑道长至少为______m。
【问题探究3】两个重要推论
1.平均速度:做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的一半。即==vt/2=
2位移差公式
(1)匀变速直线运动中,在连续相等的时间T内的位移之差为一恒定值,即Δx=x2-x1=aT2.
(2)应用:a.判断物体是否做匀变速直线运动:
如果Δx=x2-x1=x3-x2=…=xn-xn-1=aT2成立,则a为一恒量,说明物体做匀变速直线运动.
b.求加速度:利用Δx=aT2,可求得a=.
3.位移中点的瞬时速度公式:做匀速直线运动的物体,在某段位移中点位置的瞬时速度.
【典型例题5】如图所示,物体从O点开始做初速度不为零的匀加速直线运动,在第一个时间T内通过位移为s1到达A点,紧接着在第二个时间T内通过位移为s2到达B点,则以下判断正确的是
A.物体运动的加速度为
B.物体运动的加速度为
C.物体在A点的速度大小为
D.物体在B点的速度大小为
【典型例题6】小球在光滑斜面上,从点静止开始下滑,通过、、各段所用时间均为。则( )
A.与位移差等于与位移差
B.通过、段的位移之比为
C.通过、点的速度之比可能为
D.通过点的瞬时速度等于通过段的平均速度
【对点训练5】做匀加速直线运动的质点,在第内和前内的平均速度之差是,则此质点运动的加速度大小为( )
A. B. C. D.
【对点训练6】从斜面上某一位置每隔0.1s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个小球后,对在斜面上滚动的小球拍下如图所示的照片(照片与实际大小相同),测得x=15cm,x=20cm.试问:
(1)小球的加速度的大小;
(2)拍摄时小球在B点时的速度的大小;
(3)A点的上方滚动的小球还有几个。
【问题探究4】解决匀变速直线运动问题的基本思路
1、→→→→
注意:x、v0、v、a均为矢量,所以解题时需要确定正方向,一般以v0的方向为正方向.
2.匀变速直线运动公式的选用
一般问题用两个基本公式可以解决,以下特殊情况下用导出公式会提高解题的速度和准确率;
(1)不涉及时间,选择v2-v02=2ax;
(2)不涉及加速度,用平均速度公式,比如纸带问题中运用==求瞬时速度;
(3)处理纸带问题时用Δx=x2-x1=aT2,xm-xn=(m-n)aT2求加速度.
3.逆向思维法:对于末速度为零的匀减速运动,采用逆向思维法,倒过来看成初速度为零的匀加速直线运动.
4.图象法:借助v-t图象(斜率、面积)分析运动过程.
v-t图线与t轴所围“面积”表示这段时间内物体的位移:t轴上方的“面积”表示位移沿正方向,t轴下方的“面积”表示位移沿负方向,如果上方与下方的“面积”大小相等,说明物体恰好回到出发点.
【典型例题7】假设某次深海探测活动中,“蛟龙号”完成海底科考任务后竖直上浮,从上浮速度为v时开始匀减速并计时,经过时间t,“蛟龙号”上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0
【典型例题8】航天飞机在平直的跑道上降落,其减速过程可以简化为两个匀减速直线运动.航天飞机以水平速度v0=100 m/s着陆后,立即打开减速阻力伞,以大小为a1=4 m/s2的加速度做匀减速直线运动,一段时间后阻力伞脱离,航天飞机以大小为a2=2.5 m/s2的加速度做匀减速直线运动直至停下.已知两个匀减速直线运动滑行的总位移x=1 370 m.求:
(1)第二个减速阶段航天飞机运动的初速度大小;
(2)航天飞机降落后滑行的总时间.
【对点训练7】航空母舰是大规模战争的重要武器,灵活起降的飞机是它的主要攻击力之一。民航客机起飞时要在2.5min内使飞机从静止加速到44m/s;而舰载飞机借助于助推装置,在2s内就可把飞机从静止加速到82.5m/s而起飞,设飞机起飞时在跑道上做匀加速直线运动,则供客机起飞的跑道长度约是航空母舰的甲板跑道长度的( )
A.40倍 B.80倍 C.400倍 D.800倍
(
0
4
体系构建
)
(
0
5
记忆清单
)
1.对位移时间关系式x=v0t+at2的理解
(1)适用条件:位移公式只适用于匀变速直线运动.
(2)矢量性:公式中x、v0、a都是矢量,应用时必须选取正方向.一般选v0的方向为正方向.
①匀加速直线运动中,a与v0同向,a取正值;匀减速直线运动中,a与v0反向,a取负值.
②若位移的计算结果为正值,说明位移方向与规定的正方向相同;若位移的计算结果为负值,说明位移方向与规定的正方向相反.
(3)两种特殊形式
①当v0=0时,x=at2,即由静止开始的匀加速直线运动的位移公式,位移x与t2成正比.
②当a=0时,x=v0t,即匀速直线运动的位移公式.
2.对公式v2-v02=2ax的理解
(1)v2-v02=2ax为矢量式,适用于匀变速直线运动,x、v0、v、a都是矢量,应用时必须选取统一的正方向,一般选初速度 v0的方向为正方向。
①匀加速直线运动,a取正值;匀减速直线运动,a取负值。
②位移与正方向相同,x取正值;位移与正方向相反,x取负值。
(2)特殊情况∶当v0=0时,公式简化为v2=2ax(物体做初速度为零的匀加速直线运动);当v=0时,公式简化为-v02=2ax(物体做匀减速直线运动直到静止),也可以视为从静止开始、末速度为v0的反向的匀加速直线运动。
(
0
6
0
1
强化训练
)
1.在平直公路上,一辆汽车以 2m/s2 的加速度从静止开始做匀加速直线运动,经过 4s 汽车行驶的路程是( )
A.6m B.8m C.12m D.16m
2.飞机着陆后匀减速滑行,它滑行的初速度是60m/s,加速度的大小是3m/s2,飞机着陆后滑行距离为( )
A.1170m B.600m C.180m D.20m
3.做匀加速直线运动的物体位移随时间变化的函数关系是,则它的初速度是( )
A.0 B. C. D.
4.一辆摩托车在平直的公路上匀加速行驶,经过路旁两相邻电线杆时的速度分别是5m/s和15m/s,已知相邻两电线杆之间的距离是20m。则摩托车的加速度是( )
A.5 m/s2 B.0.5m/s2 C.10 m/s2 D.2.5 m/s2
5.一质点做直线运动的图像如图所示,由图像可知( )
A.质点沿x轴正方向做匀速运动 B.质点沿x轴负方向做匀速运动
C.时,质点的速度是5m/s D.时,质点的速度是
6.蓝牙小音箱可以在一定距离内与手机等设备实现连接,某型号的蓝牙音箱无线连接的有效距离是。在两条平行且靠近的直轨道上,分别放置智能小车A、B,两车分别携带该型号音箱和手机。某时刻两车相距同时开始相向而行,速度大小随时间变化图像均如图所示。则手机与音箱从相互连接到断开连接持续的时间为( )
A. B. C. D.
7.如图是实验中得到的一条纸带,A、B、C、D、E、F、G为7个相邻的计数点,相邻的两个计数点之间还有四个点未画出。量出相邻的计数点之间的距离分别为:SAB=4.20cm、SBC=4.65cm、SCD=5.10cm、SDE=5.54cm、SEF=6.00cm、SFG=6.46cm,已知打点计时器的工作周期为0.02s,则小车的加速度a=( )m/s2。(结果保留2位有效数字)
A.0.45 B.45 C.0.41 D.41
8.冰壶是冬奥会的一个竞赛项目。如图为我国运动员在北京冬奥会比赛中投掷冰壶的情形,冰壶以某一初速度被投出后做匀减速直线运动,用时停止,已知停止运动前最后内位移大小为,则冰壶的初速度大小为( )
A. B. C. D.
9.从静止开始做匀加速直线运动的物体,通过前一半位移和后一半位移所用时间的比值为( )
A. B.
C. D.
10.做匀加速直线运动的物体,通过A、B两点的速度分别为v和3v,则该物体( )
A.通过A、B中点时的速度为
B.通过A、B中点时的速度为2v
C.由A到B运动一半时间时的速度为v
D.由A到B运动一半时间时的速度为2v
11.北京时间2022年11月20日晩上23:00时,第22届世界杯在卡塔尔正式开幕,图为一个足球被踢出后每隔0.1s拍下的频闪照片,,,,,由此可以判定( )
A.足球做匀变速直线运动
B.足球的加速度大小为
C.足球的初速度大小
D.整个过程中足球的平均速度大小为8m/s
12.歼-20隐形战斗机首架技术验证机于2011年1月11日进行首次升空飞行测试,距今刚好十周年。已知某次训练中,歼-20着陆后经过4.5s停下来,若这个过程可看作是匀减速直线运动,则歼-20着陆后的第1s和第2s位移大小之比为( )
A.4:3 B.2:1 C.5:3 D.9:7
13.据了解,CR300AF型复兴号动车组是拥有完全自主国产研发的中国标准动车组体系中的新车型。该车型设计时速为300千米每小时,外观呈淡蓝色,除此之外复兴号动车组全车覆盖免费wifi,且每两个座椅有一个插座。假设一列复兴号动车进站时从某时刻起做匀减速直线运动,分别用时3s、2s、1s连续通过三段位移后停下,则这三段位移的平均速度之比是 ( )
A.9:4:1 B.27:8:1 C.5:3:1 D.3:2:1
14.如图所示,木块A、B并排且固定在水平桌面上,A的长度是L,B的长度是2L,一颗子弹沿水平方向以速度v1射入A,以速度v2穿出B,子弹可视为质点,其运动视为匀变速直线运动,则子弹穿出A时的速度为( )
A. B. C. D.v1
15.如图所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18 m。该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5 m/s2。此路段允许行驶的最大速度为12.5 m/s。下列说法中正确的有( )
A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线
B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速
C.如果立即做匀减速运动,在绿灯熄灭前汽车可能通过停车线
D.如果距停车线5 m处减速,汽车能停在停车线处
16.某一学习小组的同学想通过打点计时器在纸带上打出的点迹来探究小车速度随时间变化的规律,实验装置如图所示。
(1)常见的打点计时器有两种:________和_______,它们使用的都是_______电源(填“直流”或“交流”),当电源频率为50Hz时,每隔______s打一个点。
(2)关于本实验,下列说法正确的是_______。
A.释放纸带的同时,接通电源
B.先接通电源打点,后释放纸带运动
C.先释放纸带运动,后接通电源打点
D.纸带上的点迹越密集,说明纸带运动的速度越小
(3)要测量小车的速度。除打点计时器(含所用电源、纸带、墨粉纸盘)外还必须使用的测量工具是_______。
(4)该小组在规范操作下得到一条点迹清晰的纸带如图所示,在纸带上依次选出7个计数点,分别标上O、A、B、C、D、E和F,每相邻的两个计数点间还有四个点未画出,打点计时器所用电源的频率是50Hz。
①每相邻两计数点的时间间隔为________s,如果测得C、D两点间距x4=2.70cm,
D、E两点间距x5=2.90cm,则打D点时小车的速度vD=________m/s(结果保留3位有效数字)。
②该同学分别算出其他各点的速度:vA=0.220m/s,vB=0.241m/s,vC=0.258m/s,vE=0.300m/s,请在如图所示的坐标系中作出小车运动的v-t图像_______,并求出小车的加速度= _______ m/s2(结果保留3位有效数字)。
17.在高速公路上,有时会发生“追尾”事故——后面的汽车撞上前面的汽车。某段平直高速公路的最高车速限制为108 km/h,设某人驾车正以最高时速沿该高速公路匀速行驶,该车刹车时产生的加速度大小为5 m/s2,该人的反应时间(从意识到应该停车到操作刹车的时间)为0.5 s。求行驶时的安全车距至少为多少?
18.随着我国高速公路的发展,越来越多的人选择开车出行,这也造成了高速路的拥堵,为此开发了电子不停车收费系统ETC,汽车分别通过ETC通道和人工收费通道的流程如图所示,假设汽车以v1=72 km/h的速度沿直线朝着收费站正常行驶,如果过ETC通道,需要在汽车运动到通道口时速度恰好减为v2=4 m/s,然后匀速通过总长度为d=16 m的通道,接着再匀加速至v1后正常行驶;如果过人工收费通道,需要恰好在中心线处匀减速至零,经过t0=20 s的时间缴费成功后,再启动汽车匀加速至v1后正常行驶,设汽车加速和减速过程中的加速度大小均为a=1 m/s2,求:
(1)汽车过ETC通道时,从开始减速到恢复正常行驶过程中的位移x;
(2)汽车通过ETC通道比通过人工收费通道节约的时间Δt。
