人教版八年级数学第十八章勾股定理教学课件
文档属性
| 名称 | 人教版八年级数学第十八章勾股定理教学课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 119.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-25 00:00:00 | ||
图片预览


文档简介
(共12张PPT)
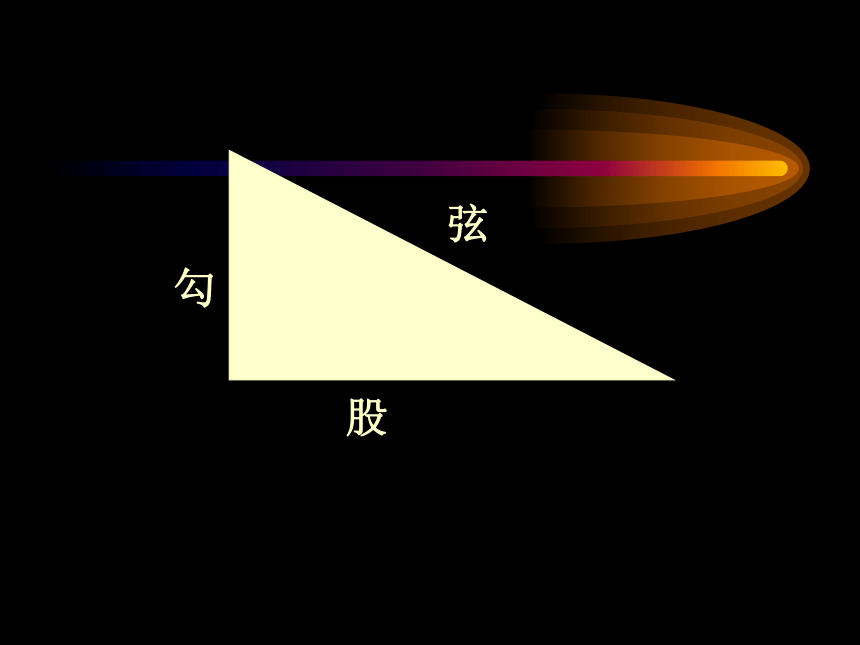
勾
股
弦
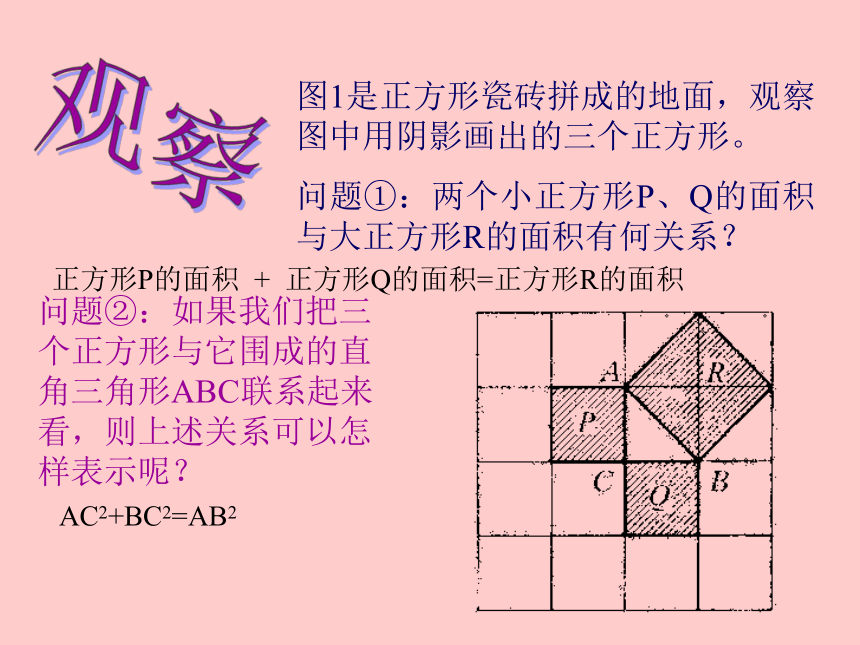
图1是正方形瓷砖拼成的地面,观察图中用阴影画出的三个正方形。
问题①:两个小正方形P、Q的面积与大正方形R的面积有何关系?
正方形P的面积 + 正方形Q的面积=正方形R的面积
问题②:如果我们把三个正方形与它围成的直角三角形ABC联系起来看,则上述关系可以怎样表示呢?
AC2+BC2=AB2
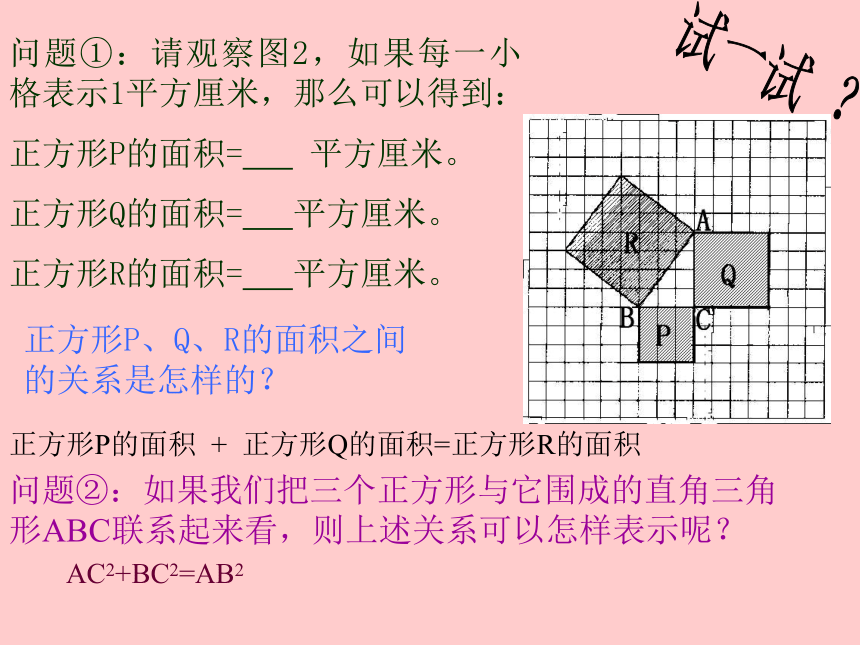
问题①:请观察图2,如果每一小格表示1平方厘米,那么可以得到:
正方形P的面积= 平方厘米。
正方形Q的面积= 平方厘米。
正方形R的面积= 平方厘米。
正方形P、Q、R的面积之间的关系是怎样的?
正方形P的面积 + 正方形Q的面积=正方形R的面积
问题②:如果我们把三个正方形与它围成的直角三角形ABC联系起来看,则上述关系可以怎样表示呢?
AC2+BC2=AB2
在方格纸上,用三角尺画直角三角形(第一小组两条直角边分别为6厘米、8厘米;第二小组两条直角边分别为5厘米、12厘米),然后用刻度尺量出斜边的长,并验证上述关系对你所画直角三角形是否成立。
问题①:根据上述结论,请猜测:任意直角三角形的两条直角边长分别为a、b,斜边为c,则这三条边之间的关系可以怎样表示呢?
a2+b2=c2
问题②:上述结论若用文字叙述,可以怎样表达呢?
直角三角形两直角边的平方和等于斜边的平方。
例题:如图3,将长为4米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底部B的距离AB.(精确到0.01米)
A
C
B
1.边长为8厘米的正方形的对角线长是多少?
巩固练习一:
2.求下列三个图中直角三角形的未知边。
5
12
c
b
10
6
9
41
a
巩固练习二:
1.在直角Rt△ABC中,AB=c, BC=a,AC=b,∠B=90°.
①已知a=6,b=10,求c.
②已知a=24,c=25,b.
2.如果一个直角三角形的两条边长分别是3厘米和4厘米,那么它的第三边的长是多少?这个三角形的周长是多少厘米?
A
C
B
本节课我们主要学习了勾股定理:直角三角形两直角边的平方和等于斜边的平方,并学习用勾股定理来解决简单的几何问题。
注意:在实际计算中除证明线段平方关系外,多用定理的变形公式.
课堂小结:
2009年3月30日
THE END
勾
股
弦
图1是正方形瓷砖拼成的地面,观察图中用阴影画出的三个正方形。
问题①:两个小正方形P、Q的面积与大正方形R的面积有何关系?
正方形P的面积 + 正方形Q的面积=正方形R的面积
问题②:如果我们把三个正方形与它围成的直角三角形ABC联系起来看,则上述关系可以怎样表示呢?
AC2+BC2=AB2
问题①:请观察图2,如果每一小格表示1平方厘米,那么可以得到:
正方形P的面积= 平方厘米。
正方形Q的面积= 平方厘米。
正方形R的面积= 平方厘米。
正方形P、Q、R的面积之间的关系是怎样的?
正方形P的面积 + 正方形Q的面积=正方形R的面积
问题②:如果我们把三个正方形与它围成的直角三角形ABC联系起来看,则上述关系可以怎样表示呢?
AC2+BC2=AB2
在方格纸上,用三角尺画直角三角形(第一小组两条直角边分别为6厘米、8厘米;第二小组两条直角边分别为5厘米、12厘米),然后用刻度尺量出斜边的长,并验证上述关系对你所画直角三角形是否成立。
问题①:根据上述结论,请猜测:任意直角三角形的两条直角边长分别为a、b,斜边为c,则这三条边之间的关系可以怎样表示呢?
a2+b2=c2
问题②:上述结论若用文字叙述,可以怎样表达呢?
直角三角形两直角边的平方和等于斜边的平方。
例题:如图3,将长为4米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底部B的距离AB.(精确到0.01米)
A
C
B
1.边长为8厘米的正方形的对角线长是多少?
巩固练习一:
2.求下列三个图中直角三角形的未知边。
5
12
c
b
10
6
9
41
a
巩固练习二:
1.在直角Rt△ABC中,AB=c, BC=a,AC=b,∠B=90°.
①已知a=6,b=10,求c.
②已知a=24,c=25,b.
2.如果一个直角三角形的两条边长分别是3厘米和4厘米,那么它的第三边的长是多少?这个三角形的周长是多少厘米?
A
C
B
本节课我们主要学习了勾股定理:直角三角形两直角边的平方和等于斜边的平方,并学习用勾股定理来解决简单的几何问题。
注意:在实际计算中除证明线段平方关系外,多用定理的变形公式.
课堂小结:
2009年3月30日
THE END
