山东省菏泽市定陶区2023-2024学年八年级下学期期中考试数学试题(含答案)
文档属性
| 名称 | 山东省菏泽市定陶区2023-2024学年八年级下学期期中考试数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 748.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 00:00:00 | ||
图片预览



文档简介
八年级数学期中样题
(2024年4月)
注意事项:
1.本试题满分120分,考试时间120分钟
2.请将答案填写在答题卡上
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置)
1.在实数,,,,,3.1415,中,无理数有( )个
A.1 B.2 C.3 D.4
2.下列计算正确的是( )
A. B. C. D.
3.若直角三角形两直角边长分别为6和7,则其斜边长度的整数部分为( )
A.9 B.10 C.8 D.7
4.如图所示,O是矩形ABCD的对角线AC的中点,E为AD的中点.若,,则的周长为( )
A.10 B. C. D.14
5.小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元,每支钢笔5元,小聪最多能买x支钢笔.可列出不等式( )
A. B.
C. D.
6.若不等式组无解,则实数a的取值范围是( )
A. B. C. D.
7.平行四边形ABCD中,对角线,,交点为点O,则边AB的取值范围为( )
A. B. C. D.
8.若方程组的解满足,则m的取值中负整数的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若,,则EF的最小值为( )
A.3 B.2 C. D.
10.如图,正方形ABCD中,,点E在边BC上,,将沿DE对折至,
延长EF交边AB于点G,连接DG、BF,给出以下结论:①;②;③;④;⑤.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
二、填空题(每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)
11.若实数m,n满足,则的值是__________.
12.如图,的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若,,则点D表示的实数为__________.
13.勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a,b,c,其中a,b均小于c,,,m是大于1的奇数,则__________(用含m的式子表示).
14.关于x的不等式组整数解共2个,则m的取值范围是__________.
15.如图,在长方形ABCD中,,,将沿对角线BD翻折,点C落在点处,交AD于点E,则线段DE的长为__________.
16.如图,已知等腰的直角边长为1,以的斜边为直角边,画第2个等腰,再以的斜边为直角边,画第3个等腰,…依此类推直到第100个等腰,则第100个等腰直角三角形的面积为__________.
三、解答题(本题共72分,把解答或证明过程写在答题卡的相应区域内)
17.(8分)计算:
(1); (2).
18.(8分)解下列不等式(组):
(1),并把解集在数轴上表示出来;
(2).
19.(8分)已知:的立方根是,的算术平方根是3,c是的整数部分.求的平方根.
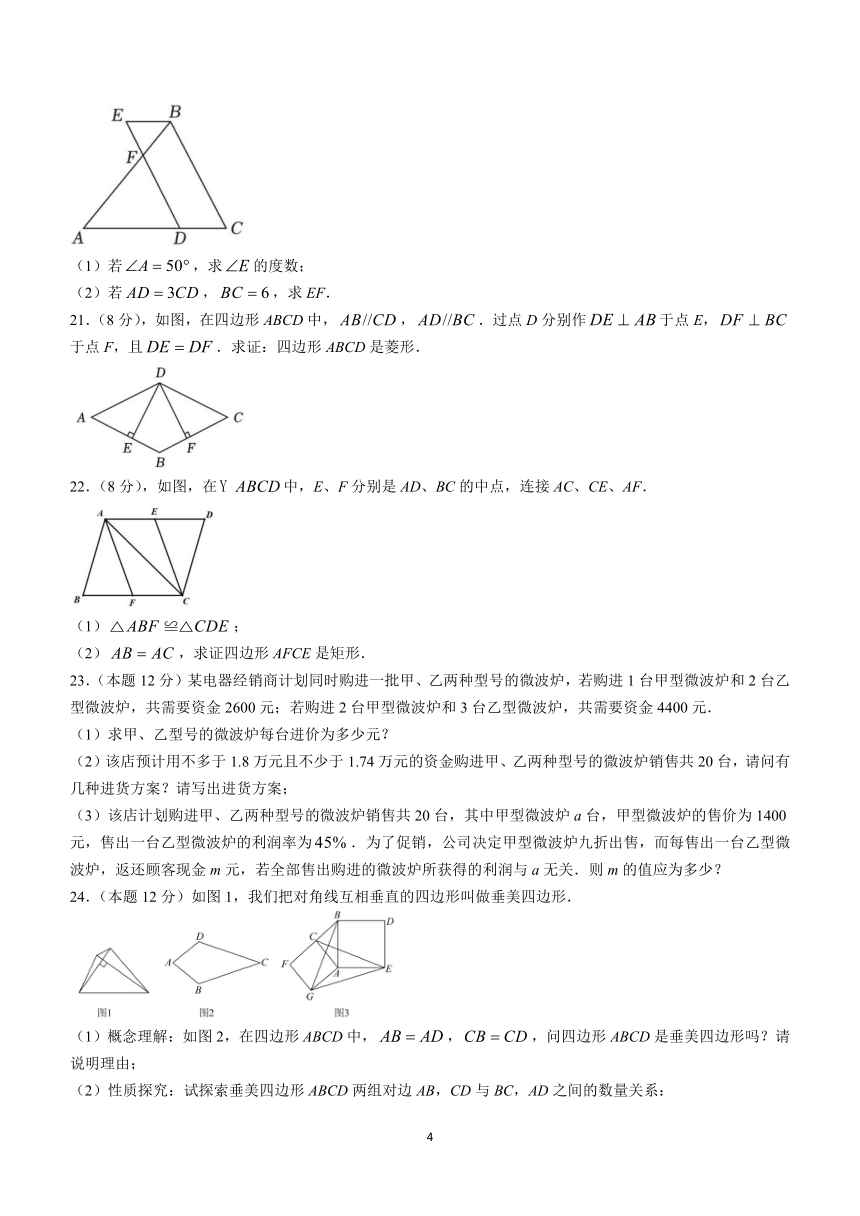
20.(8分)如图,在中,,点D在AC边上,以CB,CD为边作,DE交AB于点F.
(1)若,求的度数;
(2)若,,求EF.
21.(8分),如图,在四边形ABCD中,,.过点D分别作于点E,于点F,且.求证:四边形ABCD是菱形.
22.(8分),如图,在中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1);
(2),求证四边形AFCE是矩形.
23.(本题12分)某电器经销商计划同时购进一批甲、乙两种型号的微波炉,若购进1台甲型微波炉和2台乙型微波炉,共需要资金2600元;若购进2台甲型微波炉和3台乙型微波炉,共需要资金4400元.
(1)求甲、乙型号的微波炉每台进价为多少元?
(2)该店预计用不多于1.8万元且不少于1.74万元的资金购进甲、乙两种型号的微波炉销售共20台,请问有几种进货方案?请写出进货方案;
(3)该店计划购进甲、乙两种型号的微波炉销售共20台,其中甲型微波炉a台,甲型微波炉的售价为1400元,售出一台乙型微波炉的利润率为.为了促销,公司决定甲型微波炉九折出售,而每售出一台乙型微波炉,返还顾客现金m元,若全部售出购进的微波炉所获得的利润与a无关.则m的值应为多少?
24.(本题12分)如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,,,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系:.请写出证明过程(先画出图形,写出已知、求证,再写出证明);
(3)问题解决:如图3,分别以的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,GE,GB,已知,,求GE的长.
八年级数学期中样题答案
(2024.04)
一、选择题(本大题共10小题,每小题3分,共30分)
1-5CDACB 6-10ADBCB
二、填空题(本大题共6小题,每小题3分,共18分)
11.5 12. 13.m 14.
15.3.75 16.
三、解答题(本题共72分,写出解答或证明过程)
17.(8分)解:解:(1)原式
.……4分
(2)原式.……4分
18.(1)解:去分母得,,
去括号得,,移项得,,合并同类项得,,
把x的系数化为1得,.……3分
在数轴上表示为:
.……4分
(2)解:
解①得:……1分
解②得:……2分
在数轴上表示:
……3分
故原不等式组无解.……4分
19.的立方根是,
,解得,……2分
的算术平方根是3,
解得,……4分
是的整数部分,
.……6分
,……7分
4的平方根是.……8分
20..解:(1)在中,,,
,
四边形BCDE是平行四边形,
;……3分
(2),
..
,.
.……8分
21.证明:于点E,于点F,,
,,
四边形ABCD是平行四边形,……3分
,……4分
在和中,
,
,……6分
,
四边形ABCD是菱形.……8分
22.(1)四边形ABCD是平行四边形,,,.
、F分别是AD、BC的中点,
,.,,
.……4分
(2),.
又,
四边形AFCE是平行四边形.……6分
,F分别是BC的中点,.
即.四边形AFCE是矩形.……8分
23.(1)解:设甲型号微波炉每台进价为x元,乙型号微波炉每台进价为y元,……1分
,……2分
解得:,……3分
答:甲型号微波炉每台进价为1000元,乙型号微波炉每台进价为800元.……4分
(2)解:设购进甲型号微波炉为a台,则乙型号微波炉为台,由(1)及题意得:……5分
,……6分
解得:,……7分
为正整数,的值为7、8、9、10,
有4种进货方案,分别为:甲型号7台则乙型号13台;甲型号8台则乙型号12台;甲型号9台则乙型号11台;甲型号10台则乙型号10台.……8分
(3)解:设总利润为w,则由(2)可得:,……10分
所获得的利润与a无关,
,解得:,……11分
答:要使所获得的利润与a无关,则m的值应为100.……12分
24.(1)解:四边形ABCD是垂美四边形.
证明:如图连接AC,BD交于点E,
,
点A在线段BD的垂直平分线上……1分
,
点C在线段BD的垂直平分线上,……2分
直线AC是线段BD的垂直平分线,
,即四边形ABCD是垂美四边形.……3分
(2)如图2,已知四边形ABCD中,垂足为E,
求证:.
证明:,,
由勾股定理得,,,
.……6分
(3)连接CG、BE,如图:
,,即,
在和中,,
.……8分
,又,
,即,
四边形CGEB是垂美四边形,……10分
由(2)得,,
在中,,,根据勾股定理可得:,
和BE分别是正方形ACFG和ABDG的对角线,
,,,
.……12分
(2024年4月)
注意事项:
1.本试题满分120分,考试时间120分钟
2.请将答案填写在答题卡上
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置)
1.在实数,,,,,3.1415,中,无理数有( )个
A.1 B.2 C.3 D.4
2.下列计算正确的是( )
A. B. C. D.
3.若直角三角形两直角边长分别为6和7,则其斜边长度的整数部分为( )
A.9 B.10 C.8 D.7
4.如图所示,O是矩形ABCD的对角线AC的中点,E为AD的中点.若,,则的周长为( )
A.10 B. C. D.14
5.小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元,每支钢笔5元,小聪最多能买x支钢笔.可列出不等式( )
A. B.
C. D.
6.若不等式组无解,则实数a的取值范围是( )
A. B. C. D.
7.平行四边形ABCD中,对角线,,交点为点O,则边AB的取值范围为( )
A. B. C. D.
8.若方程组的解满足,则m的取值中负整数的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若,,则EF的最小值为( )
A.3 B.2 C. D.
10.如图,正方形ABCD中,,点E在边BC上,,将沿DE对折至,
延长EF交边AB于点G,连接DG、BF,给出以下结论:①;②;③;④;⑤.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
二、填空题(每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)
11.若实数m,n满足,则的值是__________.
12.如图,的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若,,则点D表示的实数为__________.
13.勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a,b,c,其中a,b均小于c,,,m是大于1的奇数,则__________(用含m的式子表示).
14.关于x的不等式组整数解共2个,则m的取值范围是__________.
15.如图,在长方形ABCD中,,,将沿对角线BD翻折,点C落在点处,交AD于点E,则线段DE的长为__________.
16.如图,已知等腰的直角边长为1,以的斜边为直角边,画第2个等腰,再以的斜边为直角边,画第3个等腰,…依此类推直到第100个等腰,则第100个等腰直角三角形的面积为__________.
三、解答题(本题共72分,把解答或证明过程写在答题卡的相应区域内)
17.(8分)计算:
(1); (2).
18.(8分)解下列不等式(组):
(1),并把解集在数轴上表示出来;
(2).
19.(8分)已知:的立方根是,的算术平方根是3,c是的整数部分.求的平方根.
20.(8分)如图,在中,,点D在AC边上,以CB,CD为边作,DE交AB于点F.
(1)若,求的度数;
(2)若,,求EF.
21.(8分),如图,在四边形ABCD中,,.过点D分别作于点E,于点F,且.求证:四边形ABCD是菱形.
22.(8分),如图,在中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1);
(2),求证四边形AFCE是矩形.
23.(本题12分)某电器经销商计划同时购进一批甲、乙两种型号的微波炉,若购进1台甲型微波炉和2台乙型微波炉,共需要资金2600元;若购进2台甲型微波炉和3台乙型微波炉,共需要资金4400元.
(1)求甲、乙型号的微波炉每台进价为多少元?
(2)该店预计用不多于1.8万元且不少于1.74万元的资金购进甲、乙两种型号的微波炉销售共20台,请问有几种进货方案?请写出进货方案;
(3)该店计划购进甲、乙两种型号的微波炉销售共20台,其中甲型微波炉a台,甲型微波炉的售价为1400元,售出一台乙型微波炉的利润率为.为了促销,公司决定甲型微波炉九折出售,而每售出一台乙型微波炉,返还顾客现金m元,若全部售出购进的微波炉所获得的利润与a无关.则m的值应为多少?
24.(本题12分)如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,,,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系:.请写出证明过程(先画出图形,写出已知、求证,再写出证明);
(3)问题解决:如图3,分别以的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,GE,GB,已知,,求GE的长.
八年级数学期中样题答案
(2024.04)
一、选择题(本大题共10小题,每小题3分,共30分)
1-5CDACB 6-10ADBCB
二、填空题(本大题共6小题,每小题3分,共18分)
11.5 12. 13.m 14.
15.3.75 16.
三、解答题(本题共72分,写出解答或证明过程)
17.(8分)解:解:(1)原式
.……4分
(2)原式.……4分
18.(1)解:去分母得,,
去括号得,,移项得,,合并同类项得,,
把x的系数化为1得,.……3分
在数轴上表示为:
.……4分
(2)解:
解①得:……1分
解②得:……2分
在数轴上表示:
……3分
故原不等式组无解.……4分
19.的立方根是,
,解得,……2分
的算术平方根是3,
解得,……4分
是的整数部分,
.……6分
,……7分
4的平方根是.……8分
20..解:(1)在中,,,
,
四边形BCDE是平行四边形,
;……3分
(2),
..
,.
.……8分
21.证明:于点E,于点F,,
,,
四边形ABCD是平行四边形,……3分
,……4分
在和中,
,
,……6分
,
四边形ABCD是菱形.……8分
22.(1)四边形ABCD是平行四边形,,,.
、F分别是AD、BC的中点,
,.,,
.……4分
(2),.
又,
四边形AFCE是平行四边形.……6分
,F分别是BC的中点,.
即.四边形AFCE是矩形.……8分
23.(1)解:设甲型号微波炉每台进价为x元,乙型号微波炉每台进价为y元,……1分
,……2分
解得:,……3分
答:甲型号微波炉每台进价为1000元,乙型号微波炉每台进价为800元.……4分
(2)解:设购进甲型号微波炉为a台,则乙型号微波炉为台,由(1)及题意得:……5分
,……6分
解得:,……7分
为正整数,的值为7、8、9、10,
有4种进货方案,分别为:甲型号7台则乙型号13台;甲型号8台则乙型号12台;甲型号9台则乙型号11台;甲型号10台则乙型号10台.……8分
(3)解:设总利润为w,则由(2)可得:,……10分
所获得的利润与a无关,
,解得:,……11分
答:要使所获得的利润与a无关,则m的值应为100.……12分
24.(1)解:四边形ABCD是垂美四边形.
证明:如图连接AC,BD交于点E,
,
点A在线段BD的垂直平分线上……1分
,
点C在线段BD的垂直平分线上,……2分
直线AC是线段BD的垂直平分线,
,即四边形ABCD是垂美四边形.……3分
(2)如图2,已知四边形ABCD中,垂足为E,
求证:.
证明:,,
由勾股定理得,,,
.……6分
(3)连接CG、BE,如图:
,,即,
在和中,,
.……8分
,又,
,即,
四边形CGEB是垂美四边形,……10分
由(2)得,,
在中,,,根据勾股定理可得:,
和BE分别是正方形ACFG和ABDG的对角线,
,,,
.……12分
同课章节目录
