第6单元运算律易错卷(单元测试)2023-2024学年数学四年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元运算律易错卷(单元测试)2023-2024学年数学四年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 58.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 00:00:00 | ||
图片预览




文档简介
第6单元运算律易错卷(单元测试)2023-2024学年数学四年级下册苏教版
一、选择题
1.369-98用简便方法计算是( )。
A.369-100-2 B.369-(100+2) C.369-100+2
2.与144÷24得数相等的算式是( )。
A.144÷3×8 B.144÷6÷4 C.144÷12÷12
3.在用竖式计算24×12的过程中所使用的运算律是( )。
A.加法结合律 B.乘法结合律 C.乘法分配律
4.A=101×99,B=101×100-101,A与B相比( )。
A.A>B B.A=B C.A<B
5.小琳计算器上数字键“4”坏了,用下面算式( )也可以算出2967×24的得数。
A.2967×12×12 B.2967×8×3 C.2967×30-6
6.如果□×☆=300,则下列算式正确的是( )。
A.(□×5)×(☆÷5)=300B.(□×5)×(☆×5)=300 C.(□÷5)×(☆÷5)=300
二、填空题
7.乘法结合律用字母表示的方法:( ),乘法交换律用字母表示的方法:( )。
8.两个数的和与一个数相乘,等于这两个数( )与这个数相乘,再把两个积( ),用字母表示为(a+b)×c=a×( )+b×( )。
9.在括号里填上“>”“<”或“=”。
450÷(9×5)( )450÷9×5 182-99( )182-100-1
125×12( )125×8+125×4 38×15( )39×14
10.丽丽在计算“25×A+22×25”时,因为粗心,算成了“(A+25)×25”,得到的结果是1000,那么正确的结果是( )。
11.在里填合适的数,并写出应用的运算律。
(1)237+141+359=237+(+359),运用了( )。
(2)36×(45+50)=36×+×,运用了( )。
12.计算下图两块地的面积(单位:米)。我们可以把两块地的面积加起来,列式是( );也可以用总长度乘宽,列式是( )。
三、判断题
13.103×28=100×28+3×28,这里运用了乘法分配律。( )
14.431-101=431-100+1。( )
15.a+202=a+200+2。( )
16.70-70÷14=0÷14=0。( )
17.甲、乙两地相距2千米,微微和华华分别从甲、乙两地同时出发,相向而行,微微每分钟行70米,华华每分钟行60米,15分钟后,他们相遇。( )
四、计算题
18.直接写出得数。
19.用简便方法计算。
129-(57+29) 210÷6÷5 45×101-45 98×87+87×2
五、解答题
20.食堂运进大米和面粉各160袋,每袋大米25千克,每袋面粉15千克。运进的大米和面粉一共多少千克?
21.小军和小红分别从一座桥的两端同时出发相向而行,小军的速度是每分钟65米,小红的速度是每分钟45米,经过6分钟两人相遇,这座桥长多少米?
22.甲、乙两对合挖一条水渠,甲队每天挖46米,乙队每天挖52米,甲、乙两队同时开工,合作12天后正好完成。这条水渠长多少米?
23.运输队有大货车和小货车各24辆,大货车的载质量是16吨,小货车的载质量是4吨。
(1)如果用这些货车运煤,一次能运多少吨?
(2)这些大货车一次要比小货车多运煤多少吨?
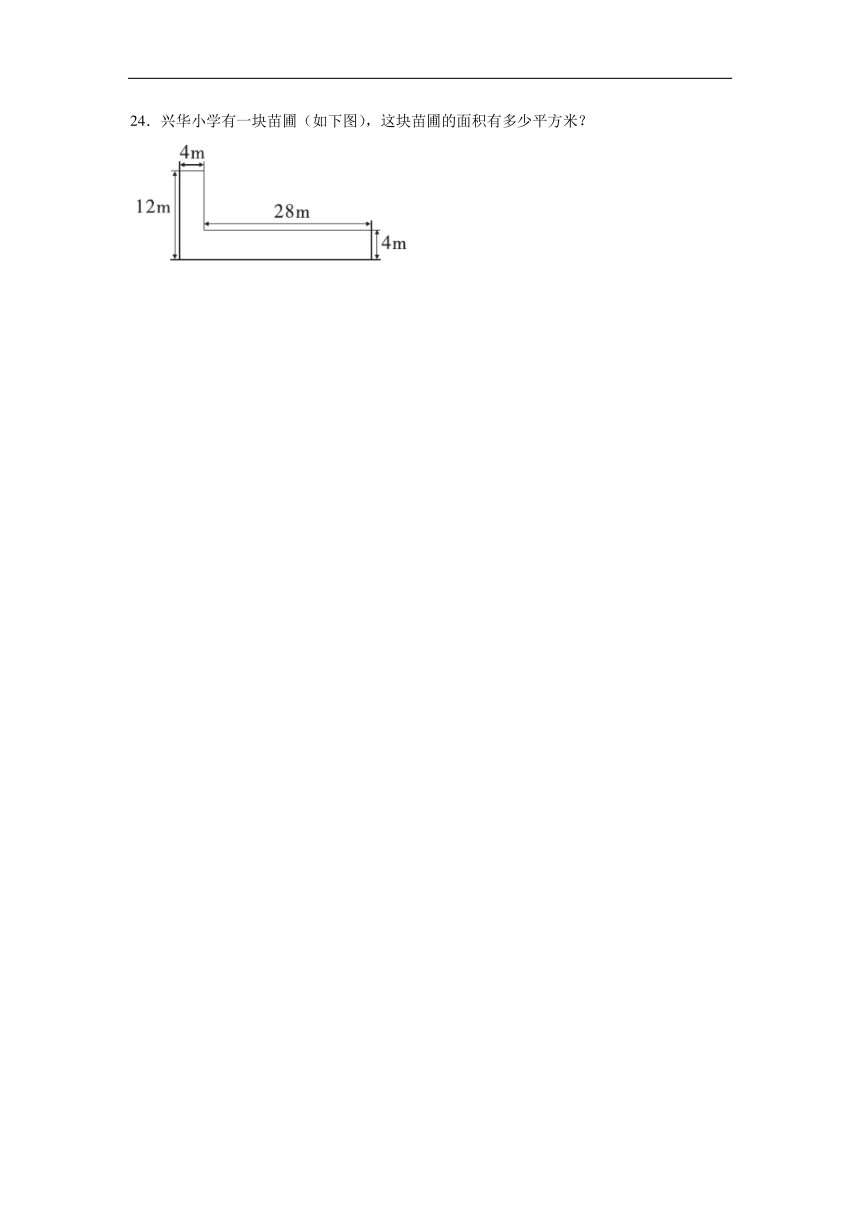
24.兴华小学有一块苗圃(如下图),这块苗圃的面积有多少平方米?
参考答案:
1.C
【分析】369-98,因为98接近整百,可以把它先看做100,就是369-100,因为100比98多2,这样一来就多减去了2,再在式子的后面把多减去的加回来,就是369-100+2。
【详解】根据分析可知:
369-98用简便方法计算是369-100+2。
故答案为:C
【点睛】简便算法变化多端,要理解算理,要熟悉数字之间存在的关系,再运用简便算法。
2.B
【分析】一个数连续除以两个数,可以除以后两个数的积,也可以先除以第二个数,再除以第一个数,商不变。据此解答即可。
【详解】24=12×2=3×8=6×4
144÷24=144÷12÷2=144÷3÷8=144÷6÷4
三个选项的算式与144÷24得数相等的算式是144÷6÷4。
故答案为:B
【点睛】理解并熟记:a÷b÷c=a÷(b×c),此关系式在有些计算中会起到简便的作用。
3.C
【分析】竖式计算24×12时,先用2乘24得到一个积,再用10乘24得到第二个积,然后把两个积相加,也就是把12分解成了(12+2),然后与24分别相乘再相加,这是运用了乘法分配律。据此解答。
【详解】由分析得:
在用竖式计算24×12的过程中所使用的运算律是乘法分配律。
故答案为:C
【点睛】乘法分配律是最常用的简便运算的方法,要熟练掌握并灵活运用。
4.B
【分析】计算101×99时,将99看成100-1,再根据乘法分配律进行计算,并与101×100-101比较大小。
【详解】A=101×99=101×(100-1)=101×100-101=B
故答案为:B
【点睛】本题考查乘法分配律的灵活应用。
5.B
【分析】乘法结合律:a×b×c=a×(b×c),据此即可解答。
【详解】2967×24=2967×(8×3)=2967×8×3
故答案为:B。
【点睛】本题主要考查学生对运算定律的掌握和灵活运用。
6.A
【分析】先把各选项的式子化简,再进行判断解答。
【详解】A.(□×5)×(☆÷5)=□×5×☆÷5=□×☆,答案正确;
B.(□×5)×(☆×5)=□×5×☆×5=□×☆×25,答案错误;
C.(□÷5)×(☆÷5)=□÷5×☆÷5=□×☆÷25,答案错误;
故选:A。
【点睛】本题的关键是把给出的式子化简,找出与原题式子的关系。
7. (a×b)×c=a×(b×c) a×b=b×a
【详解】三个数相乘,可以先把前两个数相乘,再乘第三个数,也可以先把后两个数相乘再和第一个数相乘,结果不变,这叫做乘法结合律。例如(16×25)×4=16×(25×4)、(65×8)×125=65×(125×8)。乘法结合律用字母表示为:(a×b)×c=a×(b×c)。两个数相乘,交换乘数的位置积不变,这叫做乘法交换律。例如5×3=3×5,20×38=38×20。乘法交换律用字母表示为:a×b=b×a。
乘法结合律用字母表示的方法:(a×b)×c=a×(b×c),乘法交换律用字母表示的方法:a×b=b×a。
8. 分别 相加 c c
【详解】两个数的和与一个数相乘,可以用这两个数分别和这个数相乘,再把它们的积相加,这叫乘法分配律。例如(25+125)×8=25×8+125×8、(72+35)×9=72×9+35×9。乘法分配律用字母表示为:(a+b)×c=a×c+b×c。
两个数的和与一个数相乘,等于这两个数(分别)与这个数相乘,再把两个积(相加),用字母表示为(a+b)×c=a×(c)+b×(c)。
9. < > = >
【分析】(1)除法的性质:a÷b÷c=a÷(b×c);先运用除法的性质把左边算式展开,然后再比较;
(2)减法的性质:a-b-c=a-(b+c);运用减法的性质把右边的算式变成182-101,然后再进行比较;
(3)乘法分配律:a×(b+c)=a×b+a×c;运用乘法分配律即可判断两个算式相等;
(4)计算出两个算式的结果再比较大小。
【详解】(1)450÷(9×5)=450÷9÷5,450÷9÷5<450÷9×5,所以450÷(9×5)<450÷9×5;
(2)182-100-1=182-(100+1)=182-101,182-99>182-101,所以182-99>182-100-1;
(3)125×12=125×(8+4)=125×8+125×4;
(4)38×15=570,39×14=546,570>546,所以38×15>39×14。
【点睛】此题主要考查了整数运算定律和整数乘法的掌握和灵活运用。
10.925
【分析】(A+25)×25=1000,用1000除以25的商再减去25,求出A的值;再把A的值代入25×A+22×25中,最后根据整数四则混合运算法则求出这个算式的结果。
【详解】(A+25)×25=1000
1000÷25=40
40-25=15
25×15+22×25
=25×(15+22)
=25×37
=925
则正确的结果是925。
【点睛】本题考查了整数的运算定律与四则混合运算,错误的结果可以求出正确的原数。
11.(1)141;加法结合律
(2)45;36;50;乘法分配律
【分析】(1)加法结合律是指三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
(2)乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。
【详解】(1)237+141+359=237+(141+359),运用了加法结合律。
(2)36×(45+50)=36×45+36×50,运用了乘法分配律。
【点睛】熟练掌握加法结合律和乘法分配律是解答此题的关键。
12. 32×15+18×15 (32+18)×15
【分析】根据长方形的面积=长×宽,既可以分别求出它们的面积,也可以先求大长方形的长和宽,再计算面积,由此解答。
【详解】把两块地的面积加起来,列式是:32×15+18×15;
拼成的长方形的长是:(32+18)米,宽是15米,用总长度乘宽,列式是:(32+18)×15。
【点睛】解答本题的关键是根据面积公式,找出所需要求的量,再列式解答。
13.√
【分析】乘法分配律:两个数的和,乘一个数,可以拆开来算,积不变,如a×(b+c)=ab+ac;由此解答。
【详解】103×28
=(100+3)×28
=100×28+3×28
这里运用了乘法分配律;
故答案为:√
【点睛】此题主要考查了乘法分配律的灵活运用,注意根据实际情况把一个因数看作两个数的和或差来简算。
14.×
【分析】在减法中,被减数减去若干个减数,可以把这些减数先加,差不变。
【详解】431-101
=431-(100+1)
=431-100-1
故答案为:×
【点睛】此题考查了减法的性质,注意100+1不要忘记带小括号。
15.√
【分析】此题a+202中的202接近200,可以把202变成200+2再运用了加法的结合律解答。
【详解】因为a+202=a+(200+2)=a+200+2。所以判断正确。
【点睛】此题202=200+2,再运用加法结合律:三个数相加,可以先把前两个数相加,再加上第三个数;或者先把后两个数相加,再加上第一个数,和不变。(a+b)+c = a+(b+c)即可解答。
16.×
【分析】解答此题要明确运算顺序,含有两级运算且没有括号的要先算乘除法再算加减法。
【详解】因为有减有除没有括号的运算顺序是先算除法再算减法。
70-70÷14=70-5=65,所以题干计算错误。故答案为:×
【点睛】明确四则混合运算的法则是解答本题的关键。
17.×
【分析】速度和×相遇时间=路程和
【详解】2千米=2000米,15×(70+60)=1950(米)2000>1950
故答案为:×
【点睛】本题考查了简单的行程问题,计算时要细心。
18.4600;4200;7700;3900;2727
750;6;10000;8;1100
【详解】略
19.43;7;4500;8700
【分析】129-(57+29)运用减法的性质简便计算;
210÷6÷5运用除法的性质简便计算;
45×101-45运用乘法分配律简便计算;
98×87+87×2运用乘法分配律简便计算。
【详解】129-(57+29)
=129-29-57
=100-57
=43
210÷6÷5
=210÷(6×5)
=210÷30
=7
45×101-45
=45×(101-1)
=45×100
=4500
98×87+87×2
=(98+2)×87
=100×87
=8700
20.6400千克
【分析】根据题意,可用每袋大米的重量乘袋数计算出大米的总重量;用每袋面粉的重量乘袋数计算出面粉总重量,最后再相加,代入数据列式解答即可。
【详解】160×25+160×15
=(25+15)×160
=40×160
=6400(千克)
答:运进的大米和面粉一共6400千克。
【点睛】此题主要考查的是乘法意义的灵活应用,此题也可用(25+15)×160解答。
21.660米
【分析】根据路程=速度×时间,分别求出两人行走的路程,再将两个路程相加,求出这座桥的总长度。
【详解】65×6+45×6
=390+270
=660(米)
答:这座桥长660米。
【点睛】本题考查相遇问题,根据路程、速度和时间之间的关系。
22.1176米
【分析】根据工作总量=工作效率×工作时间,分别求出两队挖水渠长度,再相加求和。
【详解】46×12+52×12
=552+624
=1176(米)
答:这条水渠长1176米。
【点睛】本题考查工程问题,关键是熟记公式工作总量=工作效率×工作时间。注意每队都挖了12天,而不是12÷2=6天。
23.(1)480吨
(2)288吨
【分析】(1)大货车的载重量乘大货车的辆数,加上小货车的载重量乘小货车的辆数即可解答;
(2)大货车的载重量乘大货车的辆数,减去小货车的载重量乘小货车的辆数即可解答;
【详解】(1)16×24+4×24
=(16+4)×24
=480(吨)
答:一次能运480吨。
(2)16×24-4×24
=(16-4)×24
=288(吨)
答:这些大货车一次要比小货车多运煤288吨。
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
24.160平方米
【分析】如下图,把苗圃分成一个长为12米、宽为4米和一个长为28米、宽为4米的两个长方形,根据“长方形的面积=长×宽”分别求出两长方形的面积,再相加即可解答。
【详解】12×4+28×4
=(12+28)×4
=160(平方米)
答:这块苗圃的面积有160平方米。
【点睛】可以把图形分成两个长方形进行计算,再求和。
一、选择题
1.369-98用简便方法计算是( )。
A.369-100-2 B.369-(100+2) C.369-100+2
2.与144÷24得数相等的算式是( )。
A.144÷3×8 B.144÷6÷4 C.144÷12÷12
3.在用竖式计算24×12的过程中所使用的运算律是( )。
A.加法结合律 B.乘法结合律 C.乘法分配律
4.A=101×99,B=101×100-101,A与B相比( )。
A.A>B B.A=B C.A<B
5.小琳计算器上数字键“4”坏了,用下面算式( )也可以算出2967×24的得数。
A.2967×12×12 B.2967×8×3 C.2967×30-6
6.如果□×☆=300,则下列算式正确的是( )。
A.(□×5)×(☆÷5)=300B.(□×5)×(☆×5)=300 C.(□÷5)×(☆÷5)=300
二、填空题
7.乘法结合律用字母表示的方法:( ),乘法交换律用字母表示的方法:( )。
8.两个数的和与一个数相乘,等于这两个数( )与这个数相乘,再把两个积( ),用字母表示为(a+b)×c=a×( )+b×( )。
9.在括号里填上“>”“<”或“=”。
450÷(9×5)( )450÷9×5 182-99( )182-100-1
125×12( )125×8+125×4 38×15( )39×14
10.丽丽在计算“25×A+22×25”时,因为粗心,算成了“(A+25)×25”,得到的结果是1000,那么正确的结果是( )。
11.在里填合适的数,并写出应用的运算律。
(1)237+141+359=237+(+359),运用了( )。
(2)36×(45+50)=36×+×,运用了( )。
12.计算下图两块地的面积(单位:米)。我们可以把两块地的面积加起来,列式是( );也可以用总长度乘宽,列式是( )。
三、判断题
13.103×28=100×28+3×28,这里运用了乘法分配律。( )
14.431-101=431-100+1。( )
15.a+202=a+200+2。( )
16.70-70÷14=0÷14=0。( )
17.甲、乙两地相距2千米,微微和华华分别从甲、乙两地同时出发,相向而行,微微每分钟行70米,华华每分钟行60米,15分钟后,他们相遇。( )
四、计算题
18.直接写出得数。
19.用简便方法计算。
129-(57+29) 210÷6÷5 45×101-45 98×87+87×2
五、解答题
20.食堂运进大米和面粉各160袋,每袋大米25千克,每袋面粉15千克。运进的大米和面粉一共多少千克?
21.小军和小红分别从一座桥的两端同时出发相向而行,小军的速度是每分钟65米,小红的速度是每分钟45米,经过6分钟两人相遇,这座桥长多少米?
22.甲、乙两对合挖一条水渠,甲队每天挖46米,乙队每天挖52米,甲、乙两队同时开工,合作12天后正好完成。这条水渠长多少米?
23.运输队有大货车和小货车各24辆,大货车的载质量是16吨,小货车的载质量是4吨。
(1)如果用这些货车运煤,一次能运多少吨?
(2)这些大货车一次要比小货车多运煤多少吨?
24.兴华小学有一块苗圃(如下图),这块苗圃的面积有多少平方米?
参考答案:
1.C
【分析】369-98,因为98接近整百,可以把它先看做100,就是369-100,因为100比98多2,这样一来就多减去了2,再在式子的后面把多减去的加回来,就是369-100+2。
【详解】根据分析可知:
369-98用简便方法计算是369-100+2。
故答案为:C
【点睛】简便算法变化多端,要理解算理,要熟悉数字之间存在的关系,再运用简便算法。
2.B
【分析】一个数连续除以两个数,可以除以后两个数的积,也可以先除以第二个数,再除以第一个数,商不变。据此解答即可。
【详解】24=12×2=3×8=6×4
144÷24=144÷12÷2=144÷3÷8=144÷6÷4
三个选项的算式与144÷24得数相等的算式是144÷6÷4。
故答案为:B
【点睛】理解并熟记:a÷b÷c=a÷(b×c),此关系式在有些计算中会起到简便的作用。
3.C
【分析】竖式计算24×12时,先用2乘24得到一个积,再用10乘24得到第二个积,然后把两个积相加,也就是把12分解成了(12+2),然后与24分别相乘再相加,这是运用了乘法分配律。据此解答。
【详解】由分析得:
在用竖式计算24×12的过程中所使用的运算律是乘法分配律。
故答案为:C
【点睛】乘法分配律是最常用的简便运算的方法,要熟练掌握并灵活运用。
4.B
【分析】计算101×99时,将99看成100-1,再根据乘法分配律进行计算,并与101×100-101比较大小。
【详解】A=101×99=101×(100-1)=101×100-101=B
故答案为:B
【点睛】本题考查乘法分配律的灵活应用。
5.B
【分析】乘法结合律:a×b×c=a×(b×c),据此即可解答。
【详解】2967×24=2967×(8×3)=2967×8×3
故答案为:B。
【点睛】本题主要考查学生对运算定律的掌握和灵活运用。
6.A
【分析】先把各选项的式子化简,再进行判断解答。
【详解】A.(□×5)×(☆÷5)=□×5×☆÷5=□×☆,答案正确;
B.(□×5)×(☆×5)=□×5×☆×5=□×☆×25,答案错误;
C.(□÷5)×(☆÷5)=□÷5×☆÷5=□×☆÷25,答案错误;
故选:A。
【点睛】本题的关键是把给出的式子化简,找出与原题式子的关系。
7. (a×b)×c=a×(b×c) a×b=b×a
【详解】三个数相乘,可以先把前两个数相乘,再乘第三个数,也可以先把后两个数相乘再和第一个数相乘,结果不变,这叫做乘法结合律。例如(16×25)×4=16×(25×4)、(65×8)×125=65×(125×8)。乘法结合律用字母表示为:(a×b)×c=a×(b×c)。两个数相乘,交换乘数的位置积不变,这叫做乘法交换律。例如5×3=3×5,20×38=38×20。乘法交换律用字母表示为:a×b=b×a。
乘法结合律用字母表示的方法:(a×b)×c=a×(b×c),乘法交换律用字母表示的方法:a×b=b×a。
8. 分别 相加 c c
【详解】两个数的和与一个数相乘,可以用这两个数分别和这个数相乘,再把它们的积相加,这叫乘法分配律。例如(25+125)×8=25×8+125×8、(72+35)×9=72×9+35×9。乘法分配律用字母表示为:(a+b)×c=a×c+b×c。
两个数的和与一个数相乘,等于这两个数(分别)与这个数相乘,再把两个积(相加),用字母表示为(a+b)×c=a×(c)+b×(c)。
9. < > = >
【分析】(1)除法的性质:a÷b÷c=a÷(b×c);先运用除法的性质把左边算式展开,然后再比较;
(2)减法的性质:a-b-c=a-(b+c);运用减法的性质把右边的算式变成182-101,然后再进行比较;
(3)乘法分配律:a×(b+c)=a×b+a×c;运用乘法分配律即可判断两个算式相等;
(4)计算出两个算式的结果再比较大小。
【详解】(1)450÷(9×5)=450÷9÷5,450÷9÷5<450÷9×5,所以450÷(9×5)<450÷9×5;
(2)182-100-1=182-(100+1)=182-101,182-99>182-101,所以182-99>182-100-1;
(3)125×12=125×(8+4)=125×8+125×4;
(4)38×15=570,39×14=546,570>546,所以38×15>39×14。
【点睛】此题主要考查了整数运算定律和整数乘法的掌握和灵活运用。
10.925
【分析】(A+25)×25=1000,用1000除以25的商再减去25,求出A的值;再把A的值代入25×A+22×25中,最后根据整数四则混合运算法则求出这个算式的结果。
【详解】(A+25)×25=1000
1000÷25=40
40-25=15
25×15+22×25
=25×(15+22)
=25×37
=925
则正确的结果是925。
【点睛】本题考查了整数的运算定律与四则混合运算,错误的结果可以求出正确的原数。
11.(1)141;加法结合律
(2)45;36;50;乘法分配律
【分析】(1)加法结合律是指三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
(2)乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。
【详解】(1)237+141+359=237+(141+359),运用了加法结合律。
(2)36×(45+50)=36×45+36×50,运用了乘法分配律。
【点睛】熟练掌握加法结合律和乘法分配律是解答此题的关键。
12. 32×15+18×15 (32+18)×15
【分析】根据长方形的面积=长×宽,既可以分别求出它们的面积,也可以先求大长方形的长和宽,再计算面积,由此解答。
【详解】把两块地的面积加起来,列式是:32×15+18×15;
拼成的长方形的长是:(32+18)米,宽是15米,用总长度乘宽,列式是:(32+18)×15。
【点睛】解答本题的关键是根据面积公式,找出所需要求的量,再列式解答。
13.√
【分析】乘法分配律:两个数的和,乘一个数,可以拆开来算,积不变,如a×(b+c)=ab+ac;由此解答。
【详解】103×28
=(100+3)×28
=100×28+3×28
这里运用了乘法分配律;
故答案为:√
【点睛】此题主要考查了乘法分配律的灵活运用,注意根据实际情况把一个因数看作两个数的和或差来简算。
14.×
【分析】在减法中,被减数减去若干个减数,可以把这些减数先加,差不变。
【详解】431-101
=431-(100+1)
=431-100-1
故答案为:×
【点睛】此题考查了减法的性质,注意100+1不要忘记带小括号。
15.√
【分析】此题a+202中的202接近200,可以把202变成200+2再运用了加法的结合律解答。
【详解】因为a+202=a+(200+2)=a+200+2。所以判断正确。
【点睛】此题202=200+2,再运用加法结合律:三个数相加,可以先把前两个数相加,再加上第三个数;或者先把后两个数相加,再加上第一个数,和不变。(a+b)+c = a+(b+c)即可解答。
16.×
【分析】解答此题要明确运算顺序,含有两级运算且没有括号的要先算乘除法再算加减法。
【详解】因为有减有除没有括号的运算顺序是先算除法再算减法。
70-70÷14=70-5=65,所以题干计算错误。故答案为:×
【点睛】明确四则混合运算的法则是解答本题的关键。
17.×
【分析】速度和×相遇时间=路程和
【详解】2千米=2000米,15×(70+60)=1950(米)2000>1950
故答案为:×
【点睛】本题考查了简单的行程问题,计算时要细心。
18.4600;4200;7700;3900;2727
750;6;10000;8;1100
【详解】略
19.43;7;4500;8700
【分析】129-(57+29)运用减法的性质简便计算;
210÷6÷5运用除法的性质简便计算;
45×101-45运用乘法分配律简便计算;
98×87+87×2运用乘法分配律简便计算。
【详解】129-(57+29)
=129-29-57
=100-57
=43
210÷6÷5
=210÷(6×5)
=210÷30
=7
45×101-45
=45×(101-1)
=45×100
=4500
98×87+87×2
=(98+2)×87
=100×87
=8700
20.6400千克
【分析】根据题意,可用每袋大米的重量乘袋数计算出大米的总重量;用每袋面粉的重量乘袋数计算出面粉总重量,最后再相加,代入数据列式解答即可。
【详解】160×25+160×15
=(25+15)×160
=40×160
=6400(千克)
答:运进的大米和面粉一共6400千克。
【点睛】此题主要考查的是乘法意义的灵活应用,此题也可用(25+15)×160解答。
21.660米
【分析】根据路程=速度×时间,分别求出两人行走的路程,再将两个路程相加,求出这座桥的总长度。
【详解】65×6+45×6
=390+270
=660(米)
答:这座桥长660米。
【点睛】本题考查相遇问题,根据路程、速度和时间之间的关系。
22.1176米
【分析】根据工作总量=工作效率×工作时间,分别求出两队挖水渠长度,再相加求和。
【详解】46×12+52×12
=552+624
=1176(米)
答:这条水渠长1176米。
【点睛】本题考查工程问题,关键是熟记公式工作总量=工作效率×工作时间。注意每队都挖了12天,而不是12÷2=6天。
23.(1)480吨
(2)288吨
【分析】(1)大货车的载重量乘大货车的辆数,加上小货车的载重量乘小货车的辆数即可解答;
(2)大货车的载重量乘大货车的辆数,减去小货车的载重量乘小货车的辆数即可解答;
【详解】(1)16×24+4×24
=(16+4)×24
=480(吨)
答:一次能运480吨。
(2)16×24-4×24
=(16-4)×24
=288(吨)
答:这些大货车一次要比小货车多运煤288吨。
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
24.160平方米
【分析】如下图,把苗圃分成一个长为12米、宽为4米和一个长为28米、宽为4米的两个长方形,根据“长方形的面积=长×宽”分别求出两长方形的面积,再相加即可解答。
【详解】12×4+28×4
=(12+28)×4
=160(平方米)
答:这块苗圃的面积有160平方米。
【点睛】可以把图形分成两个长方形进行计算,再求和。
