第5单元解决问题的策略易错卷(单元测试)2023-2024学年数学四年级下册苏教版(含解析)
文档属性
| 名称 | 第5单元解决问题的策略易错卷(单元测试)2023-2024学年数学四年级下册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 134.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 08:29:26 | ||
图片预览




文档简介
第5单元解决问题的策略易错卷(单元测试)2023-2024学年数学四年级下册苏教版
一、选择题
1.学校运动会要排成6×6的方阵,如果想排成一个8×8的方阵,那么需要增加( )人。
A.8 B.18 C.28
2.小羽和小彤去文具店买同样的笔记本,小羽买了5本,小彤买了8本,____________。笔记本的单价是多少元?选择下面( )条件不能解决这个问题。
A.小羽比小彤少花21元 B.小彤用去56元 C.他们各自带了80元
3.有一张长方形的彩纸,宽10厘米,如果它的宽缩短4厘米,面积就比原来减少72平方厘米。原来的长方形彩纸的面积是( )平方厘米。
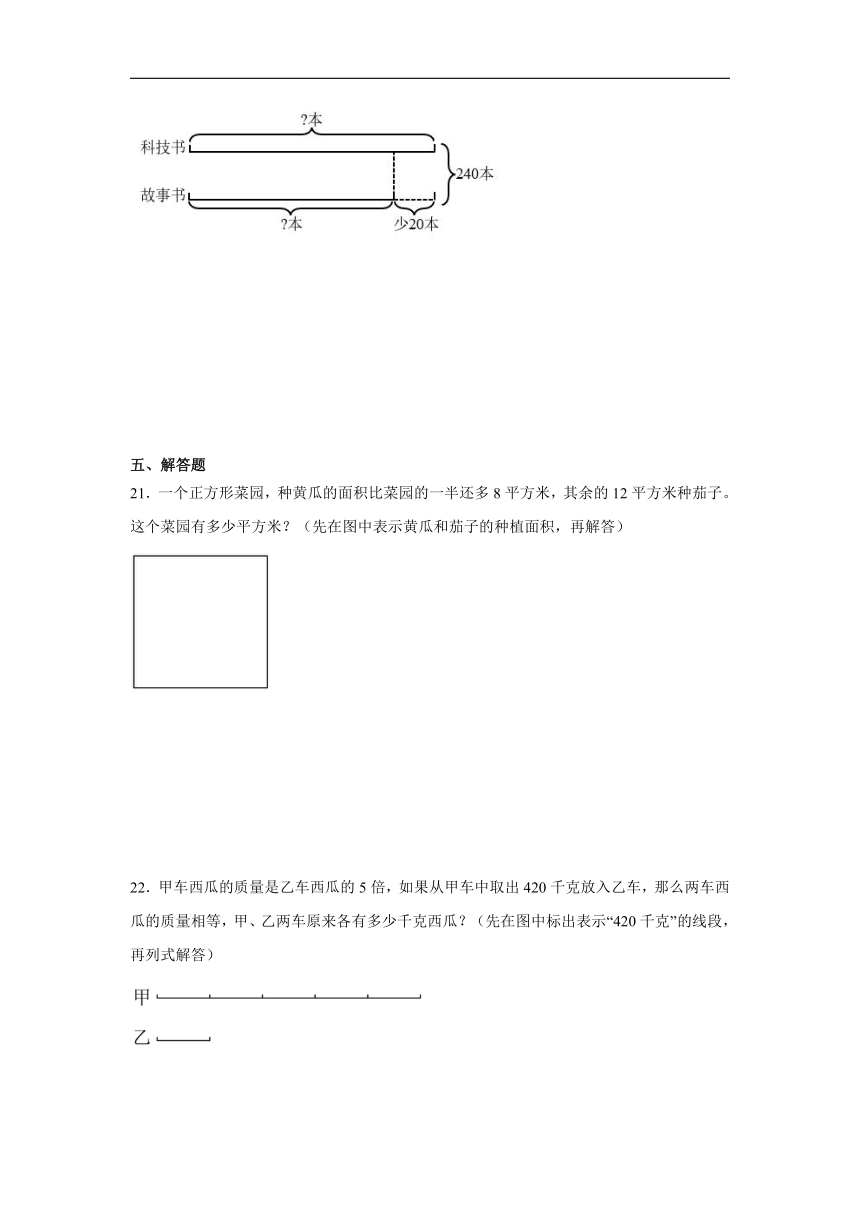
A.108 B.180 C.240
4.小明和小春共有邮票86枚,小春比小明少12枚,小明有邮票( )。
A.49枚 B.37枚 C.24枚
5.小林正开车行驶在高速公路上,他注视着他行驶的千米数,碰巧看到目前所显示的是一个左右对称的五位数13931。小林继续开着他的车,两个小时之后,他再次注视里程表,他吃惊的发现又是一个左右对称的五位数。假设他的时速不超过每小时70千米,那么小林开车的时速是( )千米/时。
A.62 B.55 C.49
6.王大叔家原来有一个长方形苗圃,长20米。扩建后苗圃的长增加5米,面积就增加75平方米。原来苗圃的面积是多少平方米?画图表示题意,正确的是( )。
A. B. C.
二、填空题
7.王林同学计划一周(7天)读完一本219页的书,已经读了3天,每天读25页,现在想要提前一天读完,余下的每天要读( )页。
8.小明和小亮一共有24枚邮票,小明比小亮多6枚,小明有( )枚邮票,小亮有( )枚邮票。
9.妈妈买一套衣服用了360元,上衣比裤子贵了40元,上衣是( )元,裤子是( )元。
10.如图,一块正方形菜地,如果边长都增加5米,面积将比原来增加875平方米。菜地原来的周长是( )米,面积是( )平方米。
11.李大伯今年栽了两行桃树和两行梨树(如图),他今年栽的桃树有( )棵,梨树有( )棵。
12.姐姐买一件上衣和一条裤子共花费880元,裤子比上衣便宜120元,一件上衣( )元。
三、判断题
13.一个表演方阵,排成7行,每行7人,最外圈有24人。( )
14.甲乙两人的邮票数同样多,如果甲给乙18张后,甲比乙少63张。( )
15.甲给乙60元两人一样多,说明原来甲比乙多60元。( )
16.计算180×40时,可以先算18×4,再在积的末尾添上两个0。( )
17.姐妹俩一共有20块糖果。姐姐给妹妹3块,姐妹俩的糖果就一样多。(20+3)÷2表示姐姐原来有多少块糖果。( )
四、计算题
18.看图列式计算。
19.看图列式计算。
20.看图列式解答。
五、解答题
21.一个正方形菜园,种黄瓜的面积比菜园的一半还多8平方米,其余的12平方米种茄子。这个菜园有多少平方米?(先在图中表示黄瓜和茄子的种植面积,再解答)
22.甲车西瓜的质量是乙车西瓜的5倍,如果从甲车中取出420千克放入乙车,那么两车西瓜的质量相等,甲、乙两车原来各有多少千克西瓜?(先在图中标出表示“420千克”的线段,再列式解答)
23.李师傅和张师傅加工同一种机器零件,8小时内,李师傅加工了14盒,张师傅加工了12盒,张师傅共比李师傅少加工36个,每盒装多少个零件?
24.两个小组去植树,一共植了56棵,其中第一组比第二组少植6棵,两个小组各植树多少棵?
(先根据题意把线段图补充完整,再解答。)
25.一个长方形菜地,青菜的面积比菜地的一半少12平方米,其余的28平方米种辣椒。
(1)下面的长方形表示长方形菜地,在图中表示出青菜和辣椒的面积。
(2)根据上面的条件,提一个用两步或两步以上计算解答的问题,并列式解答。
参考答案:
1.C
【分析】6×6的方阵中,总人数是(6×6)人。8×8的方阵中,总人数是(8×8)人。则需要增加(8×8-6×6)人。
【详解】8×8-6×6
=64-36
=28(人)
需要增加28人。
故答案为:C
【点睛】本题考查方阵问题,关键是明确总人数=行数×每行人数。
2.C
【分析】单价=总价÷数量,只要知道笔记本的总价和数量就可以求出笔记本的单价,据此即可解答。
【详解】A.小羽比小彤少买:8-5=3(本),小羽比小彤少花21元,用21除以3即等于笔记本的单价。
B.小彤买了8本,小彤用去56元,用56除以8即等于笔记本的单价。
C.他们各自带了80元,并没有说买笔记本用了多少元,不知笔记本总价,所以不能求出笔记本的单价。
故答案为:C
【点睛】熟练掌握总价、单价和数量三者之间的关系是解答本题的关键。
3.B
【分析】宽缩短4厘米,那么面积就比原来减少72平方厘米,根据长方形的面积=长×宽,用72除以4求出它的长,再用它的长乘10即可解答。
【详解】72÷4=18(厘米)
18×10=180(平方厘米)
原来的长方形彩纸的面积是180平方厘米。
故答案为:B
【点睛】比原来减少的面积即宽为4厘米的长方形的面积,是解答此题的关键。
4.A
【分析】已知大小两个数的和与它们的差,求大、小两个数的问题;
解答方法:
小数=(和-差)÷2,大数=和-小数。
【详解】(86-12)÷2
=74÷2
=37(枚)
86-37=49(枚)
所以小明有邮票49枚。
故答案为:A
【点睛】本题考查的是和差问题,熟练掌握分析中的方法是解答此题的关键。
5.B
【分析】据题意可知,她的时速不超过70公里每小时,70×2=140,两小时内她行的总路程不会超过140公里,13931+140=14071,则两个小时之后里程表上的不超过14071;则13931~14071之间的数中,只有14041这个数左右对称,所以这个数是14041。(14041-13931)÷2=55千米/时,开车的时速是55千米/时。
【详解】因为她的时速不超过70公里每小时,
70×2=140(千米)
13931+140=14071(千米)
所以两个小时之后里程表上的不超过14071,
所以这个数左右对称是14041;
(14041-13931)÷2
=110÷2
=55(千米/时)
则开车的时速是55千米/时。
故答案为:B
【点睛】完成本题的关键是抓住“时速不超过70公里每小时”这个条件求出它第二次看到的数是多少,进而求出两小内她行的里程数。
6.A
【分析】根据题意,因为用长增加5米后,面积增加75平方米,用增加的面积除以5,即可求出原来长方形的宽,再根据长方形的面积=长×宽,把数据代入公式解答。
【详解】
75÷5×20
=15×20
=300(平方米)
故答案为:A
【点睛】此题主要考查长方形面积公式的灵活运用,关键是理解题意,看清楚题中的条件,根据增加的面积和增加的长来确定正确的示意图。
7.48
【分析】每天读的页数乘读的天数可算出已经读了(25×3)页,书的总页数减去已经读的页数可以算出还剩(219-25×3)页,现在想要提前一天读完,则还需读(7-1-3)天,剩下的页数除以还要读的天数即可算出余下的每天要读几页。
【详解】(219-25×3)÷(7-1-3)
=(219-75)÷(6-3)
=144÷3
=48(页)
王林同学计划一周(7天)读完一本219页的书,已经读了3天,每天读25页,现在想要提前一天读完,余下的每天要读(48)页。
【点睛】此题考查的是整数四则混合运算在实际生活中的应用,熟练掌握整数四则混合运算顺序是解题关键。
8. 15 9
【分析】用一共邮票数减去小明比小亮多6枚,剩下的数相当于2倍小亮邮票数,即可求出小亮和小明各自邮票数。
【详解】24-6=18(枚)
18÷2=9(枚)
9+6=15(枚)
即小明有15枚邮票,小亮有9枚邮票。
【点睛】做题关键是分析题目条件,根据条件进行列式。
9. 200 160
【分析】(和+差)÷2=大数,和-大数=小数;360加40的和除以2等于上衣的价钱,360减上衣的价钱等于裤子的价钱;据此即可解答。
【详解】(360+40)÷2
=400÷2
=200(元)
360-200=160(元)
上衣是200元,裤子是160元。
【点睛】熟练掌握和差问题解题方法是解答本题的关键。
10. 340 7225
【分析】如图,增加的面积可以分为3部分,2个完全相同的长方形和一个正方形,长方形的长是原来正方形的边长,宽是5米;正方形的边长是5米。正方形的面积=边长×边长,把数据代入公式计算出增加部分小正方形的面积,增加的总面积减去正方形的面积再除以2就是长方形面积。长方形的面积=长×宽,则长=面积÷宽,把数据代入算出长方形的长,也就是原来正方形的边长。正方形的周长=边长×4,正方形的面积=边长×边长,把数据代入计算即可。
【详解】5×5=25(平方米)
(875-25)÷2
=850÷2
=425(平方米)
425÷5=85(米)
85×4=340(米)
85×85=7225(平方米)
一块正方形菜地,如果边长都增加5米,面积将比原来增加875平方米。菜地原米的周长是(340)米,面积是(7225)平方米。
【点睛】画图整理已知条件,能使题目一目了然,是解决问题的好策略。
11. 100 80
【分析】如果每行梨树增加20棵,则每行桃树和梨树同样多。每行梨树增加20棵,2行梨树增加(20×2)棵,总棵数就是(360+20×2)棵,梨树增加后的总棵数除以4即可算出每行桃树的棵数,每行桃树的棵数减去20棵即可算出每行梨树的棵数。
【详解】360+20×2
=360+40
=400(棵)
400÷4=100(棵)
100-20=80(棵)
李大伯今年栽了两行桃树和两行梨树(如图),他今年栽的桃树有(100)棵,梨树有(80)棵。
【点睛】本题考查了画线段图分析数量关系,要能看图正确分析数量关系。
12.500
【分析】用裤子和上衣的总花费+120即可求出两件上衣的价钱,再除以2即可求出每件上衣多少元,据此列式解答。
【详解】(880+120)÷2
=1000÷2
=500(元)
一件上衣500元。
【点睛】本题考查的是和差倍问题,小数=(和-差)÷2,大数=(和+差)÷2。
13.√
【分析】这个方阵共7行,每行7人,则最外圈的人数是(7-1)×4人。
【详解】(7-1)×4
=6×4
=24(人)
则最外圈有24人,题干说法正确。
故答案为:√
【点睛】本题考查方阵问题,最外圈人数=(每边人数-1)×4。
14.×
【分析】设甲乙两人的邮票都是20张,甲给乙18张后甲有(20-18)张,乙有(20+18)张,用现在乙的邮票张数减去甲的邮票张数即可。
【详解】20-18=2(张)
20+18=38(张)
38-2=36(张)
所以甲比乙少36张,题干说法错误。
故答案为:×
【点睛】采用赋值法解决问题可使题目简洁易懂,是解决问题的好策略。
15.×
【分析】若甲比乙多60元,那么给乙给60元后,则乙就比甲的钱多了。甲给乙60元后,两人的钱一样多,说明甲比乙多2个60元,给了1个60元后,那么两人的钱数就是一样多的。
【详解】60×2=120(元),甲比乙多120元。
故答案为:×
【点睛】和差问题中,把甲比乙多出来钱数的一半给乙,那么此时两人的钱数是一样的。
16.√
【分析】因数末尾有0的乘法的口算方法:先计算两个乘数0前面的数的积,再看乘数末尾一共有几个0,就在积的末尾添上几个0。
【详解】180×40=7200
所以计算180×40时,可以先算18×4,再在积的末尾添上两个0;所以原题说法正确。
故答案为:√。
【点睛】解答本题关键是熟练掌握计算法则正确进行计算。
17.×
【分析】根据题意,两人一共有20块糖果,姐姐给妹妹3块,姐妹俩的糖果就一样多,由此可知:姐姐比妹妹多(3×2)块,根据和差问题,(两数和+差)÷2=较大数,据此解答。
【详解】由分析可知:求姐姐原来有多少块糖果列式为:
(20+6)÷2
=26÷2
=13(块)
故答案为:×
【点睛】本题属于“和差问题”,根据(两数和+差)÷2=较大数,据此解答即可。
18.96平方米
【分析】
已知小长方形的面积是40平方米,宽是5米,用40÷5求出小长方形的长是多少米,小长方形的长也是大长方形的宽,再用大长方形的长乘宽,即可得大长方形的面积。
【详解】40÷5×12
=8×12
=96(平方米)
19.9米
【分析】
通过观察图可知一共有4条线段,共长39米,其中前3条线段同样长,第4条线段比前3段同样长的线段长3米,求3段同样长的线段每段是多少米?
这是一个和差问题,用总的长度减去3米,就是4条同样长的线段的和,再除以4,就是3段同样长的线段每段是多少米。
【详解】(39-3)÷4
=36÷4
=9(米)
即图中较短的线段长9米。
20.科技书:130本;故事书:110本
【分析】故事书比科技书少20本,用240减去20再除以2,求出故事书的本数,进而求出科技书的本数。
【详解】(240-20)÷2
=220÷2
=110(本)
110+20=130(本)
则科技书130本,故事书110本。
21.
图见详解;40平方米
【分析】根据题意画出能简单表示黄瓜和茄子的种植面积的图,结合“种黄瓜的面积比菜园的一半还多8平方米,其余的12平方米种茄子”,则种植茄子的面积比菜园一半的面积少8平方米,茄子种植面积是12平方米,所以菜地的面积=(种茄子的面积+8)×2,据此解答。
【详解】如图:
(12+8)×2
=20×2
=40(平方米)
答:这个菜园有40平方米。
【点睛】解答本题的关键是找出已知种茄子的面积与菜地面积一半的关系。
22.甲车原来有1050千克西瓜,乙车原来有210千克西瓜
【分析】根据线段图可知需要将甲的2格线段放入乙,可使甲乙两车质量相等,据此画出对应的线段图,结合已知质量的关系列算式进行计算即可。
【详解】线段图如下:
根据线段图可乙的重量是放入420千克的一半
420÷2=210(千克)
210×5=1050(千克)
答:甲车原来有1050千克西瓜,乙车原来有210千克西瓜。
23.18个
【分析】用张师傅比李师傅少加工的个数除以张师傅共比李师傅少加工的盒数,即可计算出每盒装多少个零件,据此即可解答。
【详解】36÷(14-12)
=36÷2
=18(个)
答:每盒装18个零件。
24.见详解图;25棵;31棵
【分析】根据题意,已知第一组比第二组少植6棵,就是在第一组线段的基础上,多画一部分表示6棵,两个括起来表示一共56棵;观察图可知用56减去6计算出第一组的2倍是多少,再除以2计算出第一组的棵数;再用第一组的棵数加上6计算出第二组的棵数,据此解答。
【详解】
(56-6)÷2
=50÷2
=25(棵)
25+6=31(棵)
答:第一组植树25棵;第二组植树31棵。
25.(1)见详解
(2)青菜地的面积是多少平方米;4平方米
【分析】(1)青菜地的面积等于菜地的一半减去12平方米,其余部分是辣椒地的面积,据此画图;
(2)青菜地的面积是多少平方米?用28减去12,求出长方形菜地面积的一半是多少平方米,再用菜地面积的一半乘2,求出长方形菜地的面积,然后用长方形菜地的面积减去辣椒地的面积,即可求出青菜地的面积是多少平方米。
【详解】(1)图如下:
(2)青菜地的面积是多少平方米?(答案不唯一)
(28-12)×2-28
=16×2-28
=32-28
=4(平方米)
答:青菜地的面积是4平方米。
一、选择题
1.学校运动会要排成6×6的方阵,如果想排成一个8×8的方阵,那么需要增加( )人。
A.8 B.18 C.28
2.小羽和小彤去文具店买同样的笔记本,小羽买了5本,小彤买了8本,____________。笔记本的单价是多少元?选择下面( )条件不能解决这个问题。
A.小羽比小彤少花21元 B.小彤用去56元 C.他们各自带了80元
3.有一张长方形的彩纸,宽10厘米,如果它的宽缩短4厘米,面积就比原来减少72平方厘米。原来的长方形彩纸的面积是( )平方厘米。
A.108 B.180 C.240
4.小明和小春共有邮票86枚,小春比小明少12枚,小明有邮票( )。
A.49枚 B.37枚 C.24枚
5.小林正开车行驶在高速公路上,他注视着他行驶的千米数,碰巧看到目前所显示的是一个左右对称的五位数13931。小林继续开着他的车,两个小时之后,他再次注视里程表,他吃惊的发现又是一个左右对称的五位数。假设他的时速不超过每小时70千米,那么小林开车的时速是( )千米/时。
A.62 B.55 C.49
6.王大叔家原来有一个长方形苗圃,长20米。扩建后苗圃的长增加5米,面积就增加75平方米。原来苗圃的面积是多少平方米?画图表示题意,正确的是( )。
A. B. C.
二、填空题
7.王林同学计划一周(7天)读完一本219页的书,已经读了3天,每天读25页,现在想要提前一天读完,余下的每天要读( )页。
8.小明和小亮一共有24枚邮票,小明比小亮多6枚,小明有( )枚邮票,小亮有( )枚邮票。
9.妈妈买一套衣服用了360元,上衣比裤子贵了40元,上衣是( )元,裤子是( )元。
10.如图,一块正方形菜地,如果边长都增加5米,面积将比原来增加875平方米。菜地原来的周长是( )米,面积是( )平方米。
11.李大伯今年栽了两行桃树和两行梨树(如图),他今年栽的桃树有( )棵,梨树有( )棵。
12.姐姐买一件上衣和一条裤子共花费880元,裤子比上衣便宜120元,一件上衣( )元。
三、判断题
13.一个表演方阵,排成7行,每行7人,最外圈有24人。( )
14.甲乙两人的邮票数同样多,如果甲给乙18张后,甲比乙少63张。( )
15.甲给乙60元两人一样多,说明原来甲比乙多60元。( )
16.计算180×40时,可以先算18×4,再在积的末尾添上两个0。( )
17.姐妹俩一共有20块糖果。姐姐给妹妹3块,姐妹俩的糖果就一样多。(20+3)÷2表示姐姐原来有多少块糖果。( )
四、计算题
18.看图列式计算。
19.看图列式计算。
20.看图列式解答。
五、解答题
21.一个正方形菜园,种黄瓜的面积比菜园的一半还多8平方米,其余的12平方米种茄子。这个菜园有多少平方米?(先在图中表示黄瓜和茄子的种植面积,再解答)
22.甲车西瓜的质量是乙车西瓜的5倍,如果从甲车中取出420千克放入乙车,那么两车西瓜的质量相等,甲、乙两车原来各有多少千克西瓜?(先在图中标出表示“420千克”的线段,再列式解答)
23.李师傅和张师傅加工同一种机器零件,8小时内,李师傅加工了14盒,张师傅加工了12盒,张师傅共比李师傅少加工36个,每盒装多少个零件?
24.两个小组去植树,一共植了56棵,其中第一组比第二组少植6棵,两个小组各植树多少棵?
(先根据题意把线段图补充完整,再解答。)
25.一个长方形菜地,青菜的面积比菜地的一半少12平方米,其余的28平方米种辣椒。
(1)下面的长方形表示长方形菜地,在图中表示出青菜和辣椒的面积。
(2)根据上面的条件,提一个用两步或两步以上计算解答的问题,并列式解答。
参考答案:
1.C
【分析】6×6的方阵中,总人数是(6×6)人。8×8的方阵中,总人数是(8×8)人。则需要增加(8×8-6×6)人。
【详解】8×8-6×6
=64-36
=28(人)
需要增加28人。
故答案为:C
【点睛】本题考查方阵问题,关键是明确总人数=行数×每行人数。
2.C
【分析】单价=总价÷数量,只要知道笔记本的总价和数量就可以求出笔记本的单价,据此即可解答。
【详解】A.小羽比小彤少买:8-5=3(本),小羽比小彤少花21元,用21除以3即等于笔记本的单价。
B.小彤买了8本,小彤用去56元,用56除以8即等于笔记本的单价。
C.他们各自带了80元,并没有说买笔记本用了多少元,不知笔记本总价,所以不能求出笔记本的单价。
故答案为:C
【点睛】熟练掌握总价、单价和数量三者之间的关系是解答本题的关键。
3.B
【分析】宽缩短4厘米,那么面积就比原来减少72平方厘米,根据长方形的面积=长×宽,用72除以4求出它的长,再用它的长乘10即可解答。
【详解】72÷4=18(厘米)
18×10=180(平方厘米)
原来的长方形彩纸的面积是180平方厘米。
故答案为:B
【点睛】比原来减少的面积即宽为4厘米的长方形的面积,是解答此题的关键。
4.A
【分析】已知大小两个数的和与它们的差,求大、小两个数的问题;
解答方法:
小数=(和-差)÷2,大数=和-小数。
【详解】(86-12)÷2
=74÷2
=37(枚)
86-37=49(枚)
所以小明有邮票49枚。
故答案为:A
【点睛】本题考查的是和差问题,熟练掌握分析中的方法是解答此题的关键。
5.B
【分析】据题意可知,她的时速不超过70公里每小时,70×2=140,两小时内她行的总路程不会超过140公里,13931+140=14071,则两个小时之后里程表上的不超过14071;则13931~14071之间的数中,只有14041这个数左右对称,所以这个数是14041。(14041-13931)÷2=55千米/时,开车的时速是55千米/时。
【详解】因为她的时速不超过70公里每小时,
70×2=140(千米)
13931+140=14071(千米)
所以两个小时之后里程表上的不超过14071,
所以这个数左右对称是14041;
(14041-13931)÷2
=110÷2
=55(千米/时)
则开车的时速是55千米/时。
故答案为:B
【点睛】完成本题的关键是抓住“时速不超过70公里每小时”这个条件求出它第二次看到的数是多少,进而求出两小内她行的里程数。
6.A
【分析】根据题意,因为用长增加5米后,面积增加75平方米,用增加的面积除以5,即可求出原来长方形的宽,再根据长方形的面积=长×宽,把数据代入公式解答。
【详解】
75÷5×20
=15×20
=300(平方米)
故答案为:A
【点睛】此题主要考查长方形面积公式的灵活运用,关键是理解题意,看清楚题中的条件,根据增加的面积和增加的长来确定正确的示意图。
7.48
【分析】每天读的页数乘读的天数可算出已经读了(25×3)页,书的总页数减去已经读的页数可以算出还剩(219-25×3)页,现在想要提前一天读完,则还需读(7-1-3)天,剩下的页数除以还要读的天数即可算出余下的每天要读几页。
【详解】(219-25×3)÷(7-1-3)
=(219-75)÷(6-3)
=144÷3
=48(页)
王林同学计划一周(7天)读完一本219页的书,已经读了3天,每天读25页,现在想要提前一天读完,余下的每天要读(48)页。
【点睛】此题考查的是整数四则混合运算在实际生活中的应用,熟练掌握整数四则混合运算顺序是解题关键。
8. 15 9
【分析】用一共邮票数减去小明比小亮多6枚,剩下的数相当于2倍小亮邮票数,即可求出小亮和小明各自邮票数。
【详解】24-6=18(枚)
18÷2=9(枚)
9+6=15(枚)
即小明有15枚邮票,小亮有9枚邮票。
【点睛】做题关键是分析题目条件,根据条件进行列式。
9. 200 160
【分析】(和+差)÷2=大数,和-大数=小数;360加40的和除以2等于上衣的价钱,360减上衣的价钱等于裤子的价钱;据此即可解答。
【详解】(360+40)÷2
=400÷2
=200(元)
360-200=160(元)
上衣是200元,裤子是160元。
【点睛】熟练掌握和差问题解题方法是解答本题的关键。
10. 340 7225
【分析】如图,增加的面积可以分为3部分,2个完全相同的长方形和一个正方形,长方形的长是原来正方形的边长,宽是5米;正方形的边长是5米。正方形的面积=边长×边长,把数据代入公式计算出增加部分小正方形的面积,增加的总面积减去正方形的面积再除以2就是长方形面积。长方形的面积=长×宽,则长=面积÷宽,把数据代入算出长方形的长,也就是原来正方形的边长。正方形的周长=边长×4,正方形的面积=边长×边长,把数据代入计算即可。
【详解】5×5=25(平方米)
(875-25)÷2
=850÷2
=425(平方米)
425÷5=85(米)
85×4=340(米)
85×85=7225(平方米)
一块正方形菜地,如果边长都增加5米,面积将比原来增加875平方米。菜地原米的周长是(340)米,面积是(7225)平方米。
【点睛】画图整理已知条件,能使题目一目了然,是解决问题的好策略。
11. 100 80
【分析】如果每行梨树增加20棵,则每行桃树和梨树同样多。每行梨树增加20棵,2行梨树增加(20×2)棵,总棵数就是(360+20×2)棵,梨树增加后的总棵数除以4即可算出每行桃树的棵数,每行桃树的棵数减去20棵即可算出每行梨树的棵数。
【详解】360+20×2
=360+40
=400(棵)
400÷4=100(棵)
100-20=80(棵)
李大伯今年栽了两行桃树和两行梨树(如图),他今年栽的桃树有(100)棵,梨树有(80)棵。
【点睛】本题考查了画线段图分析数量关系,要能看图正确分析数量关系。
12.500
【分析】用裤子和上衣的总花费+120即可求出两件上衣的价钱,再除以2即可求出每件上衣多少元,据此列式解答。
【详解】(880+120)÷2
=1000÷2
=500(元)
一件上衣500元。
【点睛】本题考查的是和差倍问题,小数=(和-差)÷2,大数=(和+差)÷2。
13.√
【分析】这个方阵共7行,每行7人,则最外圈的人数是(7-1)×4人。
【详解】(7-1)×4
=6×4
=24(人)
则最外圈有24人,题干说法正确。
故答案为:√
【点睛】本题考查方阵问题,最外圈人数=(每边人数-1)×4。
14.×
【分析】设甲乙两人的邮票都是20张,甲给乙18张后甲有(20-18)张,乙有(20+18)张,用现在乙的邮票张数减去甲的邮票张数即可。
【详解】20-18=2(张)
20+18=38(张)
38-2=36(张)
所以甲比乙少36张,题干说法错误。
故答案为:×
【点睛】采用赋值法解决问题可使题目简洁易懂,是解决问题的好策略。
15.×
【分析】若甲比乙多60元,那么给乙给60元后,则乙就比甲的钱多了。甲给乙60元后,两人的钱一样多,说明甲比乙多2个60元,给了1个60元后,那么两人的钱数就是一样多的。
【详解】60×2=120(元),甲比乙多120元。
故答案为:×
【点睛】和差问题中,把甲比乙多出来钱数的一半给乙,那么此时两人的钱数是一样的。
16.√
【分析】因数末尾有0的乘法的口算方法:先计算两个乘数0前面的数的积,再看乘数末尾一共有几个0,就在积的末尾添上几个0。
【详解】180×40=7200
所以计算180×40时,可以先算18×4,再在积的末尾添上两个0;所以原题说法正确。
故答案为:√。
【点睛】解答本题关键是熟练掌握计算法则正确进行计算。
17.×
【分析】根据题意,两人一共有20块糖果,姐姐给妹妹3块,姐妹俩的糖果就一样多,由此可知:姐姐比妹妹多(3×2)块,根据和差问题,(两数和+差)÷2=较大数,据此解答。
【详解】由分析可知:求姐姐原来有多少块糖果列式为:
(20+6)÷2
=26÷2
=13(块)
故答案为:×
【点睛】本题属于“和差问题”,根据(两数和+差)÷2=较大数,据此解答即可。
18.96平方米
【分析】
已知小长方形的面积是40平方米,宽是5米,用40÷5求出小长方形的长是多少米,小长方形的长也是大长方形的宽,再用大长方形的长乘宽,即可得大长方形的面积。
【详解】40÷5×12
=8×12
=96(平方米)
19.9米
【分析】
通过观察图可知一共有4条线段,共长39米,其中前3条线段同样长,第4条线段比前3段同样长的线段长3米,求3段同样长的线段每段是多少米?
这是一个和差问题,用总的长度减去3米,就是4条同样长的线段的和,再除以4,就是3段同样长的线段每段是多少米。
【详解】(39-3)÷4
=36÷4
=9(米)
即图中较短的线段长9米。
20.科技书:130本;故事书:110本
【分析】故事书比科技书少20本,用240减去20再除以2,求出故事书的本数,进而求出科技书的本数。
【详解】(240-20)÷2
=220÷2
=110(本)
110+20=130(本)
则科技书130本,故事书110本。
21.
图见详解;40平方米
【分析】根据题意画出能简单表示黄瓜和茄子的种植面积的图,结合“种黄瓜的面积比菜园的一半还多8平方米,其余的12平方米种茄子”,则种植茄子的面积比菜园一半的面积少8平方米,茄子种植面积是12平方米,所以菜地的面积=(种茄子的面积+8)×2,据此解答。
【详解】如图:
(12+8)×2
=20×2
=40(平方米)
答:这个菜园有40平方米。
【点睛】解答本题的关键是找出已知种茄子的面积与菜地面积一半的关系。
22.甲车原来有1050千克西瓜,乙车原来有210千克西瓜
【分析】根据线段图可知需要将甲的2格线段放入乙,可使甲乙两车质量相等,据此画出对应的线段图,结合已知质量的关系列算式进行计算即可。
【详解】线段图如下:
根据线段图可乙的重量是放入420千克的一半
420÷2=210(千克)
210×5=1050(千克)
答:甲车原来有1050千克西瓜,乙车原来有210千克西瓜。
23.18个
【分析】用张师傅比李师傅少加工的个数除以张师傅共比李师傅少加工的盒数,即可计算出每盒装多少个零件,据此即可解答。
【详解】36÷(14-12)
=36÷2
=18(个)
答:每盒装18个零件。
24.见详解图;25棵;31棵
【分析】根据题意,已知第一组比第二组少植6棵,就是在第一组线段的基础上,多画一部分表示6棵,两个括起来表示一共56棵;观察图可知用56减去6计算出第一组的2倍是多少,再除以2计算出第一组的棵数;再用第一组的棵数加上6计算出第二组的棵数,据此解答。
【详解】
(56-6)÷2
=50÷2
=25(棵)
25+6=31(棵)
答:第一组植树25棵;第二组植树31棵。
25.(1)见详解
(2)青菜地的面积是多少平方米;4平方米
【分析】(1)青菜地的面积等于菜地的一半减去12平方米,其余部分是辣椒地的面积,据此画图;
(2)青菜地的面积是多少平方米?用28减去12,求出长方形菜地面积的一半是多少平方米,再用菜地面积的一半乘2,求出长方形菜地的面积,然后用长方形菜地的面积减去辣椒地的面积,即可求出青菜地的面积是多少平方米。
【详解】(1)图如下:
(2)青菜地的面积是多少平方米?(答案不唯一)
(28-12)×2-28
=16×2-28
=32-28
=4(平方米)
答:青菜地的面积是4平方米。
