第二章整式的加减导学案(全章)
文档属性
| 名称 | 第二章整式的加减导学案(全章) |  | |
| 格式 | zip | ||
| 文件大小 | 634.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-24 11:54:35 | ||
图片预览




文档简介
班级: 姓名: 第 小组
第二章 整式的加减
2.1 整式
第1课时
【学习目标】
1、会用含有字母的式子表示数量关系;
2、掌握书写含有字母的式子的方法和注意事项。
3、体会从具体到抽象的认识过程,发展符号意识.
【学习重点】会用含有字母的式子表示数量关系。
【学习难点】寻找实际问题中各数量之间的关系,感受“抽象”的数学思想.
【预习导学】
带着学习目标自主学习课本第 54 页至 56 页内容,尝试完成以下问题 ( http: / / zk. / " \o "欢迎登陆全品中考网 ):
1、列车在冻土地段的行驶速度是100km/h,那么,
(1)列车2h行驶的路程是 km;
(2)列车4h行驶的路程是 km;
(3)列车th行驶的路程是 km;
(4)字母t表示时间有什么意义
(5)如果列车行驶速度为v km/h,行驶th列车行驶的路程是多少?
(6)回顾以前所学知识,你还能举出用字母表示数或数量关系的例子吗?
2、列代数式
(1)边长为的正方体的表面积为________,体积为 ;
(2)苹果原价是每千克p元,按8折优惠出售,用式子表示现价为 ;
(3)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量为 ;
(4)一个长方体包装盒的长和宽都是 cm,高是h cm,用式子表示它的体积为 ;
(5) 设n是一个数,则它的相反数是________.
【合作探究一】
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
(3)礼堂第1排有20个座位,后面每排都比前一排多一个座位。你能用式子表示第 n 排的座位数吗?
【合作探究二】
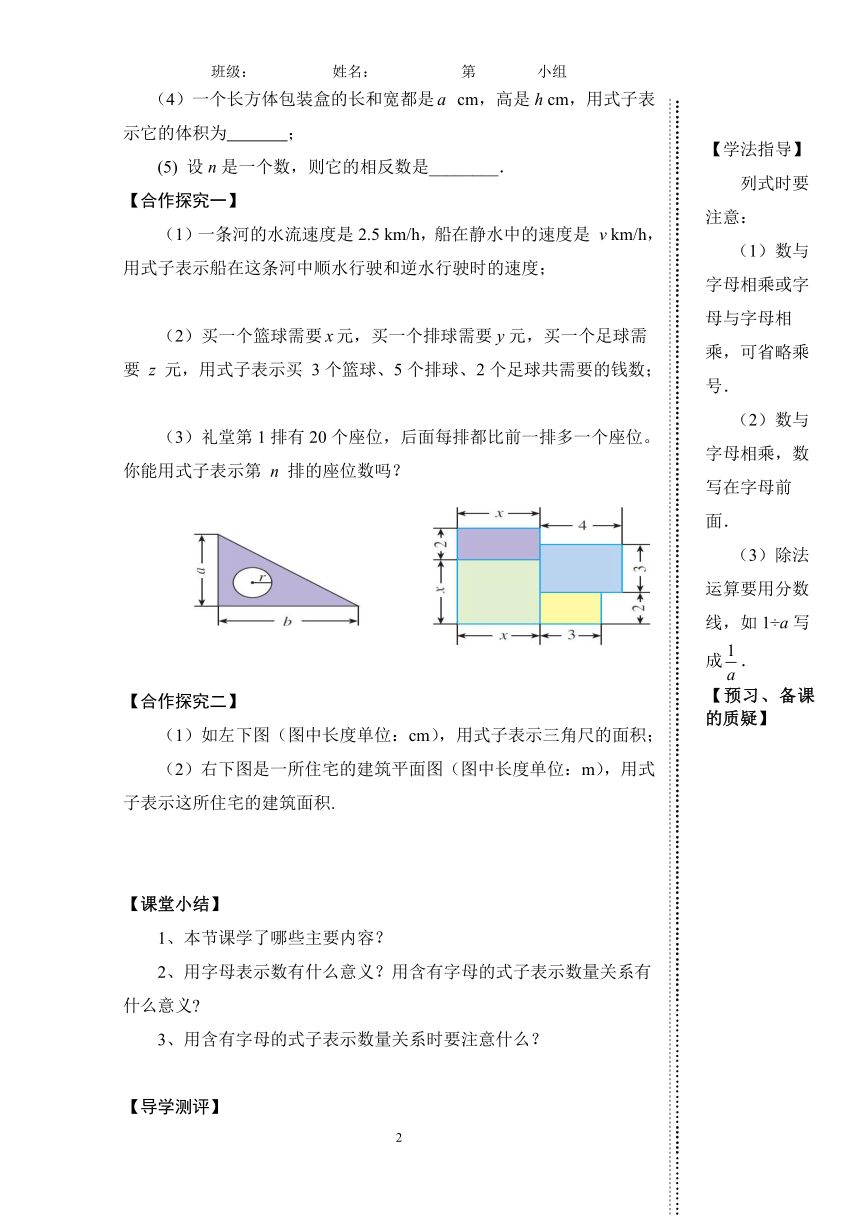
(1)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
(2)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
【课堂小结】
1、本节课学了哪些主要内容?
2、用字母表示数有什么意义?用含有字母的式子表示数量关系有什么意义
3、用含有字母的式子表示数量关系时要注意什么?
【导学测评】
1、填空:
(1)一个数比的2倍小5,则这个数为 ;
(2)全校学生总数是,其中女生占总数52%,则女生人数是 ,男生人数是 ;
(3)某校前年购买计算机台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,则学校三年共购买计算机 台;
(4)某班有名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共 本;
(5)一个两位数,十位上的数字为,个位上的数字为b,则这个两位数为 .
2、列代数式:
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
(3)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是 mm,小正方形的边长是b mm,用式子表示剩余部分的面积.
3、选择:
(1)为庆祝战胜利70周年,我市某楼盘让利于民,决定将原价为元/米2的商品房价降价10%销售,降价后的销售价为( )
A.-10% B. 10%
C.(1-10%) D.(1+10%)
(2)某商店举办促销活动,促销的方法是将原价x元的衣服以() 元出售,则下列说法中,能正确表达该商店促销方法的是( )
A.原价减去10元后再打8折
B.原价打8折后再减去10元
C.原价减去10元后再打2折
D.原价打2折后再减去10元
第二章 整式的加减
2.1 整式
第2课时
【学习目标】
1、理解单项式的概念,能熟练找出单项式的系数和次数。
2、学会用单项式表示实际问题中的数量关系。
3、经历单项式概念的形成过程,体会用字母表示数的优越性。
【学习重点】单项式、单项式的系数、单项式的次数的概念。
【学习难点】用单项式表示实际问题中的数量关系。
【预习导学】
请同学们阅读课本P56“思考”并尝试完成下面的问题:
(1)若正方体的棱长为a,则它的体积是 ;
(2)铅笔的单价是x元,圆珠笔的单价是铅笔的3.5倍,圆珠笔的单价是 ;
(3)一辆汽车的速度是v千米/小时,行驶t小时所走的路程是 千米;
(4)设n是一个不为0的数,则它的平方的相反数是 。
请观察所列代数式包含哪些运算,有何共同特征?
【归纳】由 或 的积组成的式子称为单项式。单独_________或___________也是单项式,如a,-5。
【合作探究一】
判断下列各代数式哪些是单项式?如果是,请分别指出它们的数字因数和各字母的指数和。
(1) ; (2)ab; (3)b2; (4); (5)y; (6)-xy2;(7)-5; (8)2πr, (9)abc,
【归纳】单项式的系数是指: 。(单项式表示数字与字母相乘时,通常把数字写在前面。)
单项式的次数是指: 。
【练一练】课本P57练习题。
【合作探究二】
1、例 用单项式填空,并指出它们的系数和次数:
(1) 每包书有12册,n包书有 册;
(2) 底边长为 cm,高为 h cm的三角形的面积是 cm2;
(3) 棱长为 cm的正方体的体积是 cm3 ;
(4)一台电视机原价元,现按原价的9折出售,这台电视机现在的售价是 元;
(5)如果一个长方形的长是0.9 m,宽是 m ,那么这个长方形的面积是 m2.
2、学习用字母表示数后,我们知道同一个式子可以表示不同的含义。你能赋予0.9一个含义吗?
3、“人人来当老师”:
以小组为单位,每个小组学生说出一个单项式,然后请另一个小组的学生回答出所说单项式的系数和次数,看哪一组题目出得正确,看哪一组回答得快而准。
【合作探究三】
1、你能确定单项式的系数和次数吗?和同学交流一下。
2、若是关于 x,y 的一个四次单项式,求m,n应满足的条件?
【课堂小结】
1、本节课学了哪些主要内容?
2、请你举例说明单项式的概念、单项式的系数和次数的概念.
【导学测评】
1、请你写出一个单项式,并使它的系数是-2,次数是4,那么该单项式可以是 。
2、对单项式“5x”,我们可以这样来解释:某人以5千米/小时的速度走了x小时,他一共走的路程是5x千米,请你对“5x”再给出另一个生活实际方面的解释_________________________________元.
3、单项式的系数是___________,次数是____________.
4、某商品标价是元,现按标价打9折出售,则售价是 元.
5、已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A. B. C. D.
6、下列代数式中,次数为4的单项式是 ( )
A. B.x C.4xy D.
7.判断下列各代数式哪些是单项式?
(1); (2); (3) ; (4)-5ab2; (5)y+x; (6)-xy2; (7)-5。
8、四个单项式a2h,2πr,abc,-m中,请说出它们的系数和次数:
单项式 a2h 2πr abc -m
系数
次数
第二章 整式的加减
2.1 整式
第3课时
【学习目标】
1、理解多项式的概念,能确定多项式的项和次数;
2、理解整式的概念,掌握单项式、多项式和整式之间的关系。
【学习重点】掌握多项式的定义、多项式的项和次数。
【学习难点】多项式的次数。
【预习导学】
1、下列说法或书写是否正确:
①1x ②-1x ③a3 ④a÷2 ⑤
⑥m的系数为1,次数为0 ⑦ 的系数为2,次数为2
2、列代数式:
(1)长方形的长与宽分别为a、b,则长方形的周长是 ;
(2)某班有男生x人,女生21人,则这个班共有学生 人;
(3)一个数比数x的2倍小3,则这个数为_________;
(4)鸡兔同笼,鸡a只,兔b只,则共有头 个,脚 只。
观察以上所得出的四个代数式与上节课所学单项式有何区别?
【归纳】
1、像上面这些代数式这样, 的和叫做多项式。在多项式中,每个单项式叫做多项式 。其中,不含字母的项,叫做 。例如,多项式有 项,它们分别是 。其中常数项是 。
2、一个多项式含有几项,就叫几项式。多项式里,次数最高项的次数,就是这个 。例如,多项式是一个 次 项式。
3、 与 统称为整式。
【练一练】:指出下列多项式的项和次数:
(1)3x-1+3x2 (2)4x3+2x-2y2
合作探究一:
判断下列说法是否正确,若错误请指出并更正。
(1)多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;
(2)多项式3n4-2n2+1的次数为4,常数项为1。
2、指出下列多项式是几次几项式。
x3-x+1; (2)x3-2x2y2+3y2
合作探究二:
如图所示,用式子表示圆环的面积.当R=15cm,r=10cm时,求圆环的面积(取3.14).
合作探究三:
1、已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的条件。
2、如图所示是一组有规律的图案,第l个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案中的基础图形个数为___ ____ (用含n的式子表示).
【练一练】:课本P58第1题及P59第2题。
【课堂小结】
1、本节课学了哪些主要内容?
2、请你举例说明多项式、多项式的项和次数及整式的概念.
【导学测评】
1.下列说法中,正确的是( )
A、单项式的系数是-2,次数是3;
B、单项式a的系数是0,次数是0 ;
C、是三次三项式;
D、单项式的次数是4,系数是
2、-a2b-ab+1是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
3.如果为四次单项式,则m= ;
4、3个球队进行单循环比赛(参加比赛的每一个队都与其他所有的队各赛一场),总的比赛场数是多少?4个队呢?5个队呢?n个队呢?
5、一个两位数,十位上的数字是,个位上的数字比十位上的数字多1,则这个两位数是__________(用表示)。
6、如图是用长度相等的小棒按一定规律摆成 1 的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有 根小棒.
第二章 整式的加减
2.2 整式的加减
第1课时
【学习目标】
1.理解同类项的概念,在具体情景中,认识同类项。
2.初步体会数学与人类生活的密切联系。
【学习重点】理解同类项的概念。
【学习难点】根据同类项的概念在多项式中找同类项。
【预习导学】
1.运用有理数的运算律计算:
(1)100×2+252×2=_______ ___,
(2)100×(-2)+252×(-2)=__________,
(3)100t+252t=____ _____,
思路点拨:根据逆用乘法对加法的分配律可得。
2.请根据上面得到结论的方法探究下面各式的结果:
(1)100t—252t=( )t
(2)3x2 + 2 x2 = ( ) x2
(3)3ab2 - 4 ab2 = ( ) ab2
上述运算有什么共同特点,你能从中得出什么规律?
【归纳】同类项的定义:
1、观察:3x2 和 2 x2 ; 3ab2 与 -4 ab2 在结构上有哪些相同点和不同点
2、归纳:_____________相同,并且_______________________也相同的项叫做同类项。____________________也是同类项。如3和-5是同类项。
合作探究一:
1、判断下列说法是否正确,正确的在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。( )
(2)2ab与-5ab是同类项。( )
(3)3x2y与-yx2是同类项。( )
(4)5ab2与-2ab2c是同类项。( )
(5)23与32是同类项。( )
2、下列各组式子中,是同类项的是( )
A、与 B、与 C、与 D、与
3、在下列各组式子中,不是同类项的一组是( )
A、 2 ,-5 B、 -0.5xy2, 3x2y
C、 -3t,200πt D、 ab2,-b2 a
合作探究二:
1、若把(s+t)、(s-t)分别看作一个整体,指出下面式子中的同类项。
(1)(s+t)-(s-t)-(s+t)+(s-t);
(2)2(s-t)+3(s-t)2-5(s-t)-8(s-t)2+(s-t)。
2、若-5a3bm+1与b2 a n+1是同类项,求(m-n)100的值.
合作探究三:
观察下列一串单项式的特点:
, , , , ,…
(1)按此规律写出第6个单项式.
(2)试猜想第n个单项式是什么?它的系数和次数分别是什么?
【课堂小结】
1、谈谈你本节课的主要收获以及存在的疑惑?
2、判别同类项时应注意哪些事项?
【导学测评】
1、判断下列各组中的两项是否是同类项:
(1) -5ab3与3a3b ( ) (2)3xy与3x ( )
(3) -5m2n3与2n3m2( ) (4)53与35 ( )
(5) x3与53 ( )
2、指出下列多项式中的同类项:
(1)3x-2y+1+3y-2x-5; (2)3x2y-2xy2+xy2-yx2;
3、k取何值时,3xky与-x2y是同类项?
4、已知2a2b4与-3a2mbn是同类项,那么m= ,n = .
5、若与是同类项,则__________.
6、某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) 水价(元/吨)
第一级 20吨以下(含20吨) 1.6
第二级 20吨—30吨(含30吨) 2.4
第三级 30吨以上 3.2
例:某用户的月用水量为32吨,按三级计量应缴交水费为:
(元)
(1)如果甲用户的月用水量为12吨,则甲需缴交的水费为 元;
(2)如果乙用户缴交的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为吨,则丙用户该月应缴交水费多少元?(用含的代数式表示,并化简)
第二章 整式的加减
2.2 整式的加减
第2课时
【学习目标】
1、掌握合并同类项的法则;
2、经历合并同类项过程,体会类比的数学思想。
【学习重点】正确合并同类项。
【学习难点】根据同类项的概念在多项式中找同类项。
【预习导学】
1.下列各组式子中是同类项的是( ).
A.-2a与a2 B.2a2b与3ab2 C.5ab2c与-b2ac D.-ab2和4ab2c
2、思考
(1) 6个人+4个人= (2) 6只羊+4只羊=
(3) 6个人+4只羊=
3、思考:具备什么特点的多项式可以合并呢?
4、因为多项式中的字母表示的是数,所以我们也可以运用交换律、结合律、分配律把多项式中的同类项进行合并.例如,
4x2+2x+7+3x-8x2-2 (找出多项式中的同类项)
= (交换律)
= (结合律)
= (分配律)
=
【归纳】:
1、把多项式中的同类项合并成一项,叫做 .
2、合并同类项法则:
(1)在合并同类项时, 的系数相加, 保持不变。
(2) 若两个同类项的系数互为相反数,则两项的和等于零。
如-3ab2+3ab2=(-3+3)ab2=0·ab2=0。
合作探究一:
1、合并下列各式的同类项:
(1)xy2-5xy2 (2)-3x2y+2x2y+3xy2-2xy2
(3)4a2+3b2+2ab-4a2-4b2
2、下面运算正确的是( )
A、 B、
C、 D、
合作探究二:
(1)求多项式2x2-5x+x2 +4x-3x2 - 2的值,其中x=。
(2)求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3。
合作探究三:
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为、,剪去的两个小直角三角形的两直角边长也分别为、.
(1)用含有、的代数式表示下图中“囧”的面积;
(2)当=6,=8时,求此时“囧”的面积.
【练一练】课本P65第1、2两题。
【课堂小结】
1、本节课学了哪些主要内容?
2、请你说说合并同类项的法则及注意事项。
【导学测评】
1.下列各题合并同类项的结果对不对?若不对,请改正。
(1)2x2+3x2=5x4; (2)3x+2y=5xy;
(3)7x2-3x2=4; (4)9a2b-9ba2=0。
合并下列各式的同类项
(1) (2)
(3) (4)
3.求多项式a2b-6ab-3a2b+5ab+2a2b的值,其中a=0.1,b=0.01;
4、先化简,再求值:
,其中,。
5.如图是2007年5月的日历表,任意圈出一竖列上相邻的三个数,发现这三个数的和不可能是( )。
A.27 B.36 C.40 D.54
第二章 整式的加减
2.2 整式的加减
第3课时
【学习目标】
知道去括号法则,会用去括号法则将整式化简;
能运用运算律探究去括号法则,体会数与式的关系。
【学习重点】去括号法则,准确应用法则将整式化简。
【学习难点】括号前面是“-”号去括号时,括号内各项变号容易产生错误。
【预习导学】
1、合并同类项:
(1) (2) (3)
(4)
2、在南昌到北京路段,如果列车通过冻土地段要t小时,那么它通过非冻土地段的时间为(t-0.1)小时,于是,冻土地段的路程为100t千米,非冻土地段的路程为120(t-0.1)千米,因此,
这段铁路全长为 :100t+120(t-0.1)千米①
冻土地段与非冻土地段相差:100t-120(t-0.1)千米 ②
上面的式子①、②都带有括号,类比数的运算,它们应如何化简?
100t+120(t-0.1)=100t+ =
100t-120(t-0.1)=100t =
我们知道,化简带有括号的整式,首先应先去括号.上面两式去括号部分变形分别为:
+120(t-0.5)= ③ -120(t-0.5)= ④
比较③、④两式,你能发现去括号时符号变化的规律吗?
【归纳】去括号的法则:
法则1: 如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号 ;
法则2: 如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号 。
合作探究一:
化简下列各式:
(1)8a+2b+(5a-b); (2)(5a-3b)-3(a2-2b);
(3)5xy2-[3xy2-(4xy2-2x2y)]+2x2y-xy2
合作探究二:
两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时.
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
合作探究三:
规定两种新运算:a*b=a+b,a#b=a-b,其中a,b为有理数.化简(a2b)*(3ab)+(5a2b)#(4ab),并求出当a=5,b=3时的值是多少
【练一练】课本P67第1、2两题。
【课堂小结】
1、本节课学了哪些主要内容?
2、请你说说去括号的法则及注意事项。
【导学测评】
1、下列各式化简正确的是( )。
A.a-(2a-b+c)=-a-b+c B.(a+b)-(-b+c)=a+2b+c
C.3a-[5b-(2c-a)]=2a-5b+2c D.a-(b+c)-d=a-b+c-d
2、下面去括号错误的是( ).
A.a2-(a-b+c)=a2-a+b-c B.5+a-2(3a-5)=5+a-6a+5
C.3a-(3a2 - 2a)=3a-a2+a D.a3-[(a2-(-b))=a3-a2-b
3、实数、在数轴上的位置如图所示,则化简的结果为( )
A.- B. C. D.
4、当a=1,b=2时,代数式a2-ab的值是 .
5、把3+[3a-2(a-1)]化简得 .
6、化简下列各式
(1) (2)
7、求下列代数式的值
(1)3(x2-2x-1)-4(3x-2)+2(x-1),其中x=-3;
(2)2x-y+(2y2-x2)-(x2+2y2),其中x=l,y=-2.
第二章 整式的加减
2.2 整式的加减
第4课时
【学习目标】
进一步熟悉去括号、合并同类项法则。
熟练掌握整式的加减运算并能进行化简求值.
学会利用整式的加减解决实际问题.
【学习重点】整式的加减。
【学习难点】化简求值及实际问题。
【预习导学】
1、计算:
(2)
2、求的值,其中。
(注:先化简,再求值。)
【归纳】整式加减的运算法则:一般地,几个整式相加减,如果有括号就先 ,然后再 。
合作探究一:
1、笔记本的单价是x(元),圆珠笔的单价是y(元),小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支买圆珠笔。
小红买笔记本花去 元,买圆珠笔花去 元,小红共花去 元;
小明买笔记本花去 元,买圆珠笔花去 元,小红共花去 元;
小红和小明共花多少钱?
小明比小红多花多少钱?
2、某校艺术班同学,每人都会弹钢琴或古筝,其中会弹钢琴的人数比会弹古筝的人数多10人,两种都会的有7人,设会弹古筝的有人,则该班同学共有多少人(用含的代数式表示).
合作探究二:
做大小两个长方形纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
做这两个纸盒共用料多少平方厘米?
做大纸盒比做小纸盒多用料多少平方厘米?
合作探究三:
1、求整式与的和。
2、求整式与的差。
【练一练】完成课本第69页课内练习第1、2、3题。
【课堂小结】
1、本节课你有哪些收获?
2、请你说说整式的加减法则及其应用。
【导学测评】
1、长方形的周长是4a+3b,长是2a+b-3,则宽是 。
2、一个代数式减去,差是,该代数式是 。
3、4(m-3n)-5(3n-10m)-13(n-2m)= 。
4、计算:(1)
(2)
5、先化简,再求值:,其中。
6、已知A=,B=,求:(1)2A+B;(2)B-3A。
7、一个两位数的个位数字是a,十位数字是b ,则这个两位数是 ,如果把它的个位数字与十位数字交换位置,试求交换后所得的两位数与原来的两位数的差。
第二章 整式的加减
复习课
【学习目标】
巩固对单项式、多项式、整式及同类项的概念理解;
熟练合并同类项的方法,提高整式加减计算能力。
【学习重点】合并同类项以及整式加减
【学习难点】去括号法则及整式化简求值。
【预习导学】
1、整式有关概念:
(1)单项式: 与 的积叫做单项式。单项式中________叫做这个单项式的系数;单项式中___________叫做这个单项式的次数;
(2)多项式:几个 的和,叫做多项式。____________ 叫做常数项。多项式中____ ________的次数,就是这个多项式的次数。
2、同类项、合并同类项:
(1)同类项:_____________________ 叫做同类项;
(2)合并同类项:__________________________ 叫做合并同类项;(3)合并同类项法则: 。
(4)去括号法则:
括号前是“+”号,______ _______________ 。
括号前是“-”号,_____________________ 。
3、整式的加减:
(1)如果有括号,应 ;
(2)去括号后,如果有同类项,再 。
合作探究一:
1. 代数式-每项系数分别是 __________.
2. 若代数式-2xayb+2与3x5y2-b是同类项,则代数式试求3a-b的值。
3、化简:
-7a2b+3ab2-{[4a2b-(2ab2-3ab)]-4ab-(11ab2b-31ab-6ab2}
合作探究二:
已知:A=2x2+3ax-2x-1, B=-x2+ax-1,且3A+6B的值与 x无关,求a的值.
合作探究三:
1、某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
2、如图,是用火柴棒拼成的图形,第1个图形需3根火柴棒,第2个图形需5根火柴棒,第3个图形需7根火柴棒,第4个图形需 根火柴棒,……,则第个图形需多少根火柴棒?
【课堂小结】
1、本节课你有哪些收获?让大家分享。
2、你觉得本单元的哪些知识点容易理解错误?要注意哪些问题?
【导学测评】
1. 计算:的结果是( )。
A.a2-5a+6; B.a2-5a-4; C.a2+a-4; D. a 2+a+6
2. 若所得的差是单项式.则m=___.n=_____,这个单项式是____________.
3.-的系数是______,次数是______.
4.单项式的和是 。
5.化简:
(1)
(2)
(3) (4)
6.已知A=,求 A-B 。
7.先化简,再求值:
(1),其中,
(2),其中x=-2,.
8、小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位: m )解答下列问题:
(1)用含有x, y 的式子表示地面的总面积;
(2) 当 时,地面的总面积是多少?若铺1的地砖的平均费用为80元,那么铺地砖的总费用是多少元
第二单元整式的加减测试卷
选择题(每题3分,共30分)
1.单项式2a的系数是( )
A.2 B.2a C.1 D.a
2.多项式+3x﹣2中,下列说法错误的是( )
A.这是一个二次三项式 B.二次项系数是1
C.一次项系数是3 D.常数项是2
3.下列各组两项中,是同类项的是( )
A.xy与﹣xy B.与 C.﹣2xy与﹣3ab D.3x2y与3xy2
4.下列计算正确的是( )
A.3a+4b=7ab B.7a-3a=4 C.3a+a=3a2 D.3a2b-4a2b=-a2b
5.绵阳到某地相距n千米,提速前火车从绵阳到某地要t小时,提速后行车时间减少了0.5小时,提速后火车的速度比原来速度快了( )
A. B. C.﹣ D.﹣
6.为庆祝战胜利70周年,我市某楼盘让利于民,决定将原价为a元/米2的商品房价降价10%销售,降价后的销售价为( )
A.a-10% B.a 10% C.a(1-10%) D.a(1+10%)
7.已知长方形的周长是45cm,一边长是acm,则这个长方形的面积是( )
A.cm2 B.a()cm2 C.cm2 D.()cm2
8.当x=1时,代数式的值是7,则当x =-1时,这个代数式的值是( )
A.7 B.3 C.1 D.-7
9.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,….
按照上述规律,第2015个单项式是( )
(A)2015x2015 (B)4029x2014 (C)4029x2015 (D)4031x2015
10.下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,...,按此规律排列,则第⑦个图形中小圆圈的个数为( )
A.21 B.24 C.27 D.30
二、填空题(每小题3分,共24分)
11.计算: .
12.单项式的系数是___________,次数是____________.
13.若单项式 与是同类项,则的值是 .
14.多项式按x的降幂排列为 .
15.甲、乙二人一起加工零件.甲平均每小时加工a个零件,加工2小时;乙平均每小时加工b个零件,加工3小时.甲、乙二人共加工零件 个.
16.如果手机通话每分钟收费元,那么通话分钟,收费 元。
17.一个多项式加上3+x一2x2。得到x2—1,则这个多项式是 .
18.如图是由火柴棒搭成的几何图案,则第n个图案中有 根火柴棒.(用含n的代数式表示)
三、计算题(第19、20小题各5分,21、22小题各6分,共22分。)
19.(2a2-1+2a)-3(a-1+a2) 20.7(m3+m2-m-1)-3(m3+m)
21.先化简后求值: 其中,
22. 小卢做一道题:“已知两个多项式A,B,计算A-B”.小卢误将A-B看作A+B,求得结果是9x2-2x+7.若B=x2+3x-2,请你帮助小卢求出A-B的正确答案.
四、解答题(每小题8分,共24分。)
23.某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.
(1)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;
(2)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?
24.某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) 水价(元/吨)
第一级 20吨以下(含20吨) 1.6
第二级 20吨﹣30吨(含30吨) 2.4
第三级 30吨以上 3.2
例:某用户的月用水量为32吨,按三级计量应缴交水费为:1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴交的水费为 元;
(2)如果乙用户缴交的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴交水费多少元?(用含a的代数式表示,并化简)
25.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的90%付款.现某客户要到该服装厂购买西装20套,领带条().
(1)若该客户按方案①购买,需付款 元(用含的代数式表示);
若该客户按方案②购买,需付款 元(用含的代数式表示).
(2)请你通过计算帮该顾客设计较为合算购买方案?
第二章整式的加减
《导学测评》参考答案
2.1 整式第1课时
1、(1)2a-5;(2)52%x,48%x;(3)(x+2x+4x);(4)(4a-25);(5)10a+b;
2、(1)4.8m元;(2)r2h;(3)a2-b2。 3、(1)C;(2)B.
2.1 整式第2课时
1、不唯一,如-2x4等;2、答案不唯一,合理就行.如:一斤鸡蛋5元钱,x斤鸡蛋的总售价是5x元. 3、,4。4、0.9a;5、D;6、D;7、(2)、(3)、(4)、(6);8、系数分别为 、2π、1、-1;次数分别为3、1、3、1。
2.1 整式第3课时
1、C、D;2、3,3,- ,- ,1;3、4;4、3,6,10,。
5、11m+1.6、5n+1。
2.2 整式的加减第1课时
1、(1)否,(2)否,(3)是,(4)是,(5)否;
2、(1)3x与-2x,-2y与3y,-5与1;(2)3x2y与-yx2,xy2与-2xy2;
3、k=2;4、m=1,n=4. 5、3. 6、(1);(2);(3)当<时,丙应缴交水费元;当<时,丙应缴交水费元;当>30时,丙应缴交水费元.
2.2 整式的加减第2课时
1、(1)2x2+3x2=5x2;(2)不可以合并;(3)7x2-3x2=4 x2;(4)对。
2、(1) ;(2)0;(3) ;(4)。
3、原式=-ab=0.001. 4、原式===19. 5、C.
2.2 整式的加减第3课时
1、C; 2、B; 3、C。 4、-1; 5、a+5; 6、(1)-x+2y;(2)-2x2-y3; 7、(1)原式=3x2-16x+3=78;(2)原式=-2x2+2x-y=2;
2.2 整式的加减第4课时
1、 ;2、2a2+b2;3、80m-40n;4、(1)7a2-3ab; (2)-3x2y+2xy;5、原式=4x3+8;6、(1) 2x3+x2+3x+2;(2)-3x3-4x2-2x-3;7、10b+a;9a-9b.
2.2 整式的加减复习课
1、D;2、3,4,-2a3b4;3、 ,6;4、-x2y+2xy2; 5、(1) (2)x+y;(3)
(4)5x2-3x-3; 6、x2-6xy+7y2 ;7、(1)原式=18x2y-6xy2=(2)原式=-3x+y2= 8、(1)(6x+2y+18);(2)45m2 ,3600元。
第二章整式的加减参考答案
一、选择题(每小题3分,共30分)
A.D.A.D.C.C.B.B.C.B.
二、填空题(每小题3分,共24分)
11.
12.系数是,次数是4.
13.5.
14.
15.(2a+3b)
16.am
17.3x2一x一4.
18.2n(n+1).
三、计算题(第19、20小题各5分,21、22小题各6分,共22分。)
19.原式=
20、原式=
21.-3x+y2,
22.7 x2-8x+11
四、解答题(每小题8分,共24分。)
23.(1)甲:①当0<ⅹ≤3时 10元;②当ⅹ>3时 10+1.2(ⅹ-3)
乙:①当0<ⅹ≤3时 8元 ②当ⅹ>3时 8+1.8(ⅹ-3)
(2)当乘坐的路程为13千米多一点,即ⅹ=14时 甲的费用23.2元,乙的费用27.8元,应乘甲种车.
24.19.2;23;当0<a≤20时1.6a、当20<a≤30时2.4a-16、当a>30时3.2a-40.
(2)设乙月用水量为x吨,根据题意得:
1.6×20+(x﹣20)×2.4=39.2,
答:乙月用水量23吨;
(3)当0<a≤20时,丙应缴交水费=1.6a(元);
当20<a≤30时,丙应缴交水费=1.6×20+2.4×(a﹣20)=2.4a﹣16(元);
当a>30时,丙应缴交水费=1.6×20+2.4×10+3.2(a﹣30)=3.2a﹣40(元).
25.(1)40x+3200;36x+3600;
(2)若x=100时,两种方案花费一样多;若x>100时,应选方案二;若x<100时,应选方案一。
【学法指导】
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
列式时要注意:
(1)数与字母相乘或字母与字母相乘,可省略乘号.
(2)数与字母相乘,数写在字母前面.
(3)除法运算要用分数线,如1÷a写成.
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
用整式表示实际问题中的数量关系和变化规律,可以从特殊值入手,借助表格等分析,由特殊到一般,由个体到整体地观察、分析问题,发现规律,并用含有字母的式子表示一般的结论,这体现了抽象的数学思想.
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来,更适合于一般规律的表达.
【预习、备课的质疑】
注意:
(1)单项式表示数与字母相乘时,通常把数字写在前面。
(2)当系数为1或-1时,这个“1”省略不写.
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【思考】多项式的每一项都包括它前面的符号吗?
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】多项式与单项式的区别与联系:
(1)多项式的次数不是所有项的次数之和;
(2)多项式的每一项都包括它前面的符号。
(3)多项式中含有运算符号“+”号或“-”号。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
①两个相同:字母相同;相同字母的指数相等。
②两个无关:与系数无关;与字母顺序无关。
③所有的常数项都是同类项。
④两个项虽然所含字母相同,但相同字母的指数不全相同就不是同类项。
【学法指导】
通常我们把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列,如:-4x2+5x+5或5+5x-4x2。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】:
合并同类项,法则不能忘,只求系数和,字母指数不变样。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
①多项式中只有同类项才能合并,不是同类项不能合并;②系数相加,字母部分不变;③确定好每一项系数的符号。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
去括号规律可以简单记为“-”变“+”不变,要变全都变。去括号时,要将括号连同它前面的符号一起去掉;当括号前带有数字因数时,这个数字要乘以括号内的每一项,切勿漏乘某些项.
一般地,先去小括号,再去中括号。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
【学法指导】
整式的加减其实就是合并同类项。在合并同类项时,当括号前是“-”,去括号时,括号里各项要变号。特别要注意书写格式
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
【学法指导】
在学习过程中,要回顾自己犯过哪些错误,反思犯错的原因,总结一下和同学们交流。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
PAGE
30
第二章 整式的加减
2.1 整式
第1课时
【学习目标】
1、会用含有字母的式子表示数量关系;
2、掌握书写含有字母的式子的方法和注意事项。
3、体会从具体到抽象的认识过程,发展符号意识.
【学习重点】会用含有字母的式子表示数量关系。
【学习难点】寻找实际问题中各数量之间的关系,感受“抽象”的数学思想.
【预习导学】
带着学习目标自主学习课本第 54 页至 56 页内容,尝试完成以下问题 ( http: / / zk. / " \o "欢迎登陆全品中考网 ):
1、列车在冻土地段的行驶速度是100km/h,那么,
(1)列车2h行驶的路程是 km;
(2)列车4h行驶的路程是 km;
(3)列车th行驶的路程是 km;
(4)字母t表示时间有什么意义
(5)如果列车行驶速度为v km/h,行驶th列车行驶的路程是多少?
(6)回顾以前所学知识,你还能举出用字母表示数或数量关系的例子吗?
2、列代数式
(1)边长为的正方体的表面积为________,体积为 ;
(2)苹果原价是每千克p元,按8折优惠出售,用式子表示现价为 ;
(3)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量为 ;
(4)一个长方体包装盒的长和宽都是 cm,高是h cm,用式子表示它的体积为 ;
(5) 设n是一个数,则它的相反数是________.
【合作探究一】
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
(3)礼堂第1排有20个座位,后面每排都比前一排多一个座位。你能用式子表示第 n 排的座位数吗?
【合作探究二】
(1)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
(2)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
【课堂小结】
1、本节课学了哪些主要内容?
2、用字母表示数有什么意义?用含有字母的式子表示数量关系有什么意义
3、用含有字母的式子表示数量关系时要注意什么?
【导学测评】
1、填空:
(1)一个数比的2倍小5,则这个数为 ;
(2)全校学生总数是,其中女生占总数52%,则女生人数是 ,男生人数是 ;
(3)某校前年购买计算机台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,则学校三年共购买计算机 台;
(4)某班有名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共 本;
(5)一个两位数,十位上的数字为,个位上的数字为b,则这个两位数为 .
2、列代数式:
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
(3)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是 mm,小正方形的边长是b mm,用式子表示剩余部分的面积.
3、选择:
(1)为庆祝战胜利70周年,我市某楼盘让利于民,决定将原价为元/米2的商品房价降价10%销售,降价后的销售价为( )
A.-10% B. 10%
C.(1-10%) D.(1+10%)
(2)某商店举办促销活动,促销的方法是将原价x元的衣服以() 元出售,则下列说法中,能正确表达该商店促销方法的是( )
A.原价减去10元后再打8折
B.原价打8折后再减去10元
C.原价减去10元后再打2折
D.原价打2折后再减去10元
第二章 整式的加减
2.1 整式
第2课时
【学习目标】
1、理解单项式的概念,能熟练找出单项式的系数和次数。
2、学会用单项式表示实际问题中的数量关系。
3、经历单项式概念的形成过程,体会用字母表示数的优越性。
【学习重点】单项式、单项式的系数、单项式的次数的概念。
【学习难点】用单项式表示实际问题中的数量关系。
【预习导学】
请同学们阅读课本P56“思考”并尝试完成下面的问题:
(1)若正方体的棱长为a,则它的体积是 ;
(2)铅笔的单价是x元,圆珠笔的单价是铅笔的3.5倍,圆珠笔的单价是 ;
(3)一辆汽车的速度是v千米/小时,行驶t小时所走的路程是 千米;
(4)设n是一个不为0的数,则它的平方的相反数是 。
请观察所列代数式包含哪些运算,有何共同特征?
【归纳】由 或 的积组成的式子称为单项式。单独_________或___________也是单项式,如a,-5。
【合作探究一】
判断下列各代数式哪些是单项式?如果是,请分别指出它们的数字因数和各字母的指数和。
(1) ; (2)ab; (3)b2; (4); (5)y; (6)-xy2;(7)-5; (8)2πr, (9)abc,
【归纳】单项式的系数是指: 。(单项式表示数字与字母相乘时,通常把数字写在前面。)
单项式的次数是指: 。
【练一练】课本P57练习题。
【合作探究二】
1、例 用单项式填空,并指出它们的系数和次数:
(1) 每包书有12册,n包书有 册;
(2) 底边长为 cm,高为 h cm的三角形的面积是 cm2;
(3) 棱长为 cm的正方体的体积是 cm3 ;
(4)一台电视机原价元,现按原价的9折出售,这台电视机现在的售价是 元;
(5)如果一个长方形的长是0.9 m,宽是 m ,那么这个长方形的面积是 m2.
2、学习用字母表示数后,我们知道同一个式子可以表示不同的含义。你能赋予0.9一个含义吗?
3、“人人来当老师”:
以小组为单位,每个小组学生说出一个单项式,然后请另一个小组的学生回答出所说单项式的系数和次数,看哪一组题目出得正确,看哪一组回答得快而准。
【合作探究三】
1、你能确定单项式的系数和次数吗?和同学交流一下。
2、若是关于 x,y 的一个四次单项式,求m,n应满足的条件?
【课堂小结】
1、本节课学了哪些主要内容?
2、请你举例说明单项式的概念、单项式的系数和次数的概念.
【导学测评】
1、请你写出一个单项式,并使它的系数是-2,次数是4,那么该单项式可以是 。
2、对单项式“5x”,我们可以这样来解释:某人以5千米/小时的速度走了x小时,他一共走的路程是5x千米,请你对“5x”再给出另一个生活实际方面的解释_________________________________元.
3、单项式的系数是___________,次数是____________.
4、某商品标价是元,现按标价打9折出售,则售价是 元.
5、已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A. B. C. D.
6、下列代数式中,次数为4的单项式是 ( )
A. B.x C.4xy D.
7.判断下列各代数式哪些是单项式?
(1); (2); (3) ; (4)-5ab2; (5)y+x; (6)-xy2; (7)-5。
8、四个单项式a2h,2πr,abc,-m中,请说出它们的系数和次数:
单项式 a2h 2πr abc -m
系数
次数
第二章 整式的加减
2.1 整式
第3课时
【学习目标】
1、理解多项式的概念,能确定多项式的项和次数;
2、理解整式的概念,掌握单项式、多项式和整式之间的关系。
【学习重点】掌握多项式的定义、多项式的项和次数。
【学习难点】多项式的次数。
【预习导学】
1、下列说法或书写是否正确:
①1x ②-1x ③a3 ④a÷2 ⑤
⑥m的系数为1,次数为0 ⑦ 的系数为2,次数为2
2、列代数式:
(1)长方形的长与宽分别为a、b,则长方形的周长是 ;
(2)某班有男生x人,女生21人,则这个班共有学生 人;
(3)一个数比数x的2倍小3,则这个数为_________;
(4)鸡兔同笼,鸡a只,兔b只,则共有头 个,脚 只。
观察以上所得出的四个代数式与上节课所学单项式有何区别?
【归纳】
1、像上面这些代数式这样, 的和叫做多项式。在多项式中,每个单项式叫做多项式 。其中,不含字母的项,叫做 。例如,多项式有 项,它们分别是 。其中常数项是 。
2、一个多项式含有几项,就叫几项式。多项式里,次数最高项的次数,就是这个 。例如,多项式是一个 次 项式。
3、 与 统称为整式。
【练一练】:指出下列多项式的项和次数:
(1)3x-1+3x2 (2)4x3+2x-2y2
合作探究一:
判断下列说法是否正确,若错误请指出并更正。
(1)多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;
(2)多项式3n4-2n2+1的次数为4,常数项为1。
2、指出下列多项式是几次几项式。
x3-x+1; (2)x3-2x2y2+3y2
合作探究二:
如图所示,用式子表示圆环的面积.当R=15cm,r=10cm时,求圆环的面积(取3.14).
合作探究三:
1、已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的条件。
2、如图所示是一组有规律的图案,第l个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案中的基础图形个数为___ ____ (用含n的式子表示).
【练一练】:课本P58第1题及P59第2题。
【课堂小结】
1、本节课学了哪些主要内容?
2、请你举例说明多项式、多项式的项和次数及整式的概念.
【导学测评】
1.下列说法中,正确的是( )
A、单项式的系数是-2,次数是3;
B、单项式a的系数是0,次数是0 ;
C、是三次三项式;
D、单项式的次数是4,系数是
2、-a2b-ab+1是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
3.如果为四次单项式,则m= ;
4、3个球队进行单循环比赛(参加比赛的每一个队都与其他所有的队各赛一场),总的比赛场数是多少?4个队呢?5个队呢?n个队呢?
5、一个两位数,十位上的数字是,个位上的数字比十位上的数字多1,则这个两位数是__________(用表示)。
6、如图是用长度相等的小棒按一定规律摆成 1 的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有 根小棒.
第二章 整式的加减
2.2 整式的加减
第1课时
【学习目标】
1.理解同类项的概念,在具体情景中,认识同类项。
2.初步体会数学与人类生活的密切联系。
【学习重点】理解同类项的概念。
【学习难点】根据同类项的概念在多项式中找同类项。
【预习导学】
1.运用有理数的运算律计算:
(1)100×2+252×2=_______ ___,
(2)100×(-2)+252×(-2)=__________,
(3)100t+252t=____ _____,
思路点拨:根据逆用乘法对加法的分配律可得。
2.请根据上面得到结论的方法探究下面各式的结果:
(1)100t—252t=( )t
(2)3x2 + 2 x2 = ( ) x2
(3)3ab2 - 4 ab2 = ( ) ab2
上述运算有什么共同特点,你能从中得出什么规律?
【归纳】同类项的定义:
1、观察:3x2 和 2 x2 ; 3ab2 与 -4 ab2 在结构上有哪些相同点和不同点
2、归纳:_____________相同,并且_______________________也相同的项叫做同类项。____________________也是同类项。如3和-5是同类项。
合作探究一:
1、判断下列说法是否正确,正确的在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。( )
(2)2ab与-5ab是同类项。( )
(3)3x2y与-yx2是同类项。( )
(4)5ab2与-2ab2c是同类项。( )
(5)23与32是同类项。( )
2、下列各组式子中,是同类项的是( )
A、与 B、与 C、与 D、与
3、在下列各组式子中,不是同类项的一组是( )
A、 2 ,-5 B、 -0.5xy2, 3x2y
C、 -3t,200πt D、 ab2,-b2 a
合作探究二:
1、若把(s+t)、(s-t)分别看作一个整体,指出下面式子中的同类项。
(1)(s+t)-(s-t)-(s+t)+(s-t);
(2)2(s-t)+3(s-t)2-5(s-t)-8(s-t)2+(s-t)。
2、若-5a3bm+1与b2 a n+1是同类项,求(m-n)100的值.
合作探究三:
观察下列一串单项式的特点:
, , , , ,…
(1)按此规律写出第6个单项式.
(2)试猜想第n个单项式是什么?它的系数和次数分别是什么?
【课堂小结】
1、谈谈你本节课的主要收获以及存在的疑惑?
2、判别同类项时应注意哪些事项?
【导学测评】
1、判断下列各组中的两项是否是同类项:
(1) -5ab3与3a3b ( ) (2)3xy与3x ( )
(3) -5m2n3与2n3m2( ) (4)53与35 ( )
(5) x3与53 ( )
2、指出下列多项式中的同类项:
(1)3x-2y+1+3y-2x-5; (2)3x2y-2xy2+xy2-yx2;
3、k取何值时,3xky与-x2y是同类项?
4、已知2a2b4与-3a2mbn是同类项,那么m= ,n = .
5、若与是同类项,则__________.
6、某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) 水价(元/吨)
第一级 20吨以下(含20吨) 1.6
第二级 20吨—30吨(含30吨) 2.4
第三级 30吨以上 3.2
例:某用户的月用水量为32吨,按三级计量应缴交水费为:
(元)
(1)如果甲用户的月用水量为12吨,则甲需缴交的水费为 元;
(2)如果乙用户缴交的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为吨,则丙用户该月应缴交水费多少元?(用含的代数式表示,并化简)
第二章 整式的加减
2.2 整式的加减
第2课时
【学习目标】
1、掌握合并同类项的法则;
2、经历合并同类项过程,体会类比的数学思想。
【学习重点】正确合并同类项。
【学习难点】根据同类项的概念在多项式中找同类项。
【预习导学】
1.下列各组式子中是同类项的是( ).
A.-2a与a2 B.2a2b与3ab2 C.5ab2c与-b2ac D.-ab2和4ab2c
2、思考
(1) 6个人+4个人= (2) 6只羊+4只羊=
(3) 6个人+4只羊=
3、思考:具备什么特点的多项式可以合并呢?
4、因为多项式中的字母表示的是数,所以我们也可以运用交换律、结合律、分配律把多项式中的同类项进行合并.例如,
4x2+2x+7+3x-8x2-2 (找出多项式中的同类项)
= (交换律)
= (结合律)
= (分配律)
=
【归纳】:
1、把多项式中的同类项合并成一项,叫做 .
2、合并同类项法则:
(1)在合并同类项时, 的系数相加, 保持不变。
(2) 若两个同类项的系数互为相反数,则两项的和等于零。
如-3ab2+3ab2=(-3+3)ab2=0·ab2=0。
合作探究一:
1、合并下列各式的同类项:
(1)xy2-5xy2 (2)-3x2y+2x2y+3xy2-2xy2
(3)4a2+3b2+2ab-4a2-4b2
2、下面运算正确的是( )
A、 B、
C、 D、
合作探究二:
(1)求多项式2x2-5x+x2 +4x-3x2 - 2的值,其中x=。
(2)求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3。
合作探究三:
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为、,剪去的两个小直角三角形的两直角边长也分别为、.
(1)用含有、的代数式表示下图中“囧”的面积;
(2)当=6,=8时,求此时“囧”的面积.
【练一练】课本P65第1、2两题。
【课堂小结】
1、本节课学了哪些主要内容?
2、请你说说合并同类项的法则及注意事项。
【导学测评】
1.下列各题合并同类项的结果对不对?若不对,请改正。
(1)2x2+3x2=5x4; (2)3x+2y=5xy;
(3)7x2-3x2=4; (4)9a2b-9ba2=0。
合并下列各式的同类项
(1) (2)
(3) (4)
3.求多项式a2b-6ab-3a2b+5ab+2a2b的值,其中a=0.1,b=0.01;
4、先化简,再求值:
,其中,。
5.如图是2007年5月的日历表,任意圈出一竖列上相邻的三个数,发现这三个数的和不可能是( )。
A.27 B.36 C.40 D.54
第二章 整式的加减
2.2 整式的加减
第3课时
【学习目标】
知道去括号法则,会用去括号法则将整式化简;
能运用运算律探究去括号法则,体会数与式的关系。
【学习重点】去括号法则,准确应用法则将整式化简。
【学习难点】括号前面是“-”号去括号时,括号内各项变号容易产生错误。
【预习导学】
1、合并同类项:
(1) (2) (3)
(4)
2、在南昌到北京路段,如果列车通过冻土地段要t小时,那么它通过非冻土地段的时间为(t-0.1)小时,于是,冻土地段的路程为100t千米,非冻土地段的路程为120(t-0.1)千米,因此,
这段铁路全长为 :100t+120(t-0.1)千米①
冻土地段与非冻土地段相差:100t-120(t-0.1)千米 ②
上面的式子①、②都带有括号,类比数的运算,它们应如何化简?
100t+120(t-0.1)=100t+ =
100t-120(t-0.1)=100t =
我们知道,化简带有括号的整式,首先应先去括号.上面两式去括号部分变形分别为:
+120(t-0.5)= ③ -120(t-0.5)= ④
比较③、④两式,你能发现去括号时符号变化的规律吗?
【归纳】去括号的法则:
法则1: 如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号 ;
法则2: 如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号 。
合作探究一:
化简下列各式:
(1)8a+2b+(5a-b); (2)(5a-3b)-3(a2-2b);
(3)5xy2-[3xy2-(4xy2-2x2y)]+2x2y-xy2
合作探究二:
两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时.
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
合作探究三:
规定两种新运算:a*b=a+b,a#b=a-b,其中a,b为有理数.化简(a2b)*(3ab)+(5a2b)#(4ab),并求出当a=5,b=3时的值是多少
【练一练】课本P67第1、2两题。
【课堂小结】
1、本节课学了哪些主要内容?
2、请你说说去括号的法则及注意事项。
【导学测评】
1、下列各式化简正确的是( )。
A.a-(2a-b+c)=-a-b+c B.(a+b)-(-b+c)=a+2b+c
C.3a-[5b-(2c-a)]=2a-5b+2c D.a-(b+c)-d=a-b+c-d
2、下面去括号错误的是( ).
A.a2-(a-b+c)=a2-a+b-c B.5+a-2(3a-5)=5+a-6a+5
C.3a-(3a2 - 2a)=3a-a2+a D.a3-[(a2-(-b))=a3-a2-b
3、实数、在数轴上的位置如图所示,则化简的结果为( )
A.- B. C. D.
4、当a=1,b=2时,代数式a2-ab的值是 .
5、把3+[3a-2(a-1)]化简得 .
6、化简下列各式
(1) (2)
7、求下列代数式的值
(1)3(x2-2x-1)-4(3x-2)+2(x-1),其中x=-3;
(2)2x-y+(2y2-x2)-(x2+2y2),其中x=l,y=-2.
第二章 整式的加减
2.2 整式的加减
第4课时
【学习目标】
进一步熟悉去括号、合并同类项法则。
熟练掌握整式的加减运算并能进行化简求值.
学会利用整式的加减解决实际问题.
【学习重点】整式的加减。
【学习难点】化简求值及实际问题。
【预习导学】
1、计算:
(2)
2、求的值,其中。
(注:先化简,再求值。)
【归纳】整式加减的运算法则:一般地,几个整式相加减,如果有括号就先 ,然后再 。
合作探究一:
1、笔记本的单价是x(元),圆珠笔的单价是y(元),小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支买圆珠笔。
小红买笔记本花去 元,买圆珠笔花去 元,小红共花去 元;
小明买笔记本花去 元,买圆珠笔花去 元,小红共花去 元;
小红和小明共花多少钱?
小明比小红多花多少钱?
2、某校艺术班同学,每人都会弹钢琴或古筝,其中会弹钢琴的人数比会弹古筝的人数多10人,两种都会的有7人,设会弹古筝的有人,则该班同学共有多少人(用含的代数式表示).
合作探究二:
做大小两个长方形纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
做这两个纸盒共用料多少平方厘米?
做大纸盒比做小纸盒多用料多少平方厘米?
合作探究三:
1、求整式与的和。
2、求整式与的差。
【练一练】完成课本第69页课内练习第1、2、3题。
【课堂小结】
1、本节课你有哪些收获?
2、请你说说整式的加减法则及其应用。
【导学测评】
1、长方形的周长是4a+3b,长是2a+b-3,则宽是 。
2、一个代数式减去,差是,该代数式是 。
3、4(m-3n)-5(3n-10m)-13(n-2m)= 。
4、计算:(1)
(2)
5、先化简,再求值:,其中。
6、已知A=,B=,求:(1)2A+B;(2)B-3A。
7、一个两位数的个位数字是a,十位数字是b ,则这个两位数是 ,如果把它的个位数字与十位数字交换位置,试求交换后所得的两位数与原来的两位数的差。
第二章 整式的加减
复习课
【学习目标】
巩固对单项式、多项式、整式及同类项的概念理解;
熟练合并同类项的方法,提高整式加减计算能力。
【学习重点】合并同类项以及整式加减
【学习难点】去括号法则及整式化简求值。
【预习导学】
1、整式有关概念:
(1)单项式: 与 的积叫做单项式。单项式中________叫做这个单项式的系数;单项式中___________叫做这个单项式的次数;
(2)多项式:几个 的和,叫做多项式。____________ 叫做常数项。多项式中____ ________的次数,就是这个多项式的次数。
2、同类项、合并同类项:
(1)同类项:_____________________ 叫做同类项;
(2)合并同类项:__________________________ 叫做合并同类项;(3)合并同类项法则: 。
(4)去括号法则:
括号前是“+”号,______ _______________ 。
括号前是“-”号,_____________________ 。
3、整式的加减:
(1)如果有括号,应 ;
(2)去括号后,如果有同类项,再 。
合作探究一:
1. 代数式-每项系数分别是 __________.
2. 若代数式-2xayb+2与3x5y2-b是同类项,则代数式试求3a-b的值。
3、化简:
-7a2b+3ab2-{[4a2b-(2ab2-3ab)]-4ab-(11ab2b-31ab-6ab2}
合作探究二:
已知:A=2x2+3ax-2x-1, B=-x2+ax-1,且3A+6B的值与 x无关,求a的值.
合作探究三:
1、某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
2、如图,是用火柴棒拼成的图形,第1个图形需3根火柴棒,第2个图形需5根火柴棒,第3个图形需7根火柴棒,第4个图形需 根火柴棒,……,则第个图形需多少根火柴棒?
【课堂小结】
1、本节课你有哪些收获?让大家分享。
2、你觉得本单元的哪些知识点容易理解错误?要注意哪些问题?
【导学测评】
1. 计算:的结果是( )。
A.a2-5a+6; B.a2-5a-4; C.a2+a-4; D. a 2+a+6
2. 若所得的差是单项式.则m=___.n=_____,这个单项式是____________.
3.-的系数是______,次数是______.
4.单项式的和是 。
5.化简:
(1)
(2)
(3) (4)
6.已知A=,求 A-B 。
7.先化简,再求值:
(1),其中,
(2),其中x=-2,.
8、小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位: m )解答下列问题:
(1)用含有x, y 的式子表示地面的总面积;
(2) 当 时,地面的总面积是多少?若铺1的地砖的平均费用为80元,那么铺地砖的总费用是多少元
第二单元整式的加减测试卷
选择题(每题3分,共30分)
1.单项式2a的系数是( )
A.2 B.2a C.1 D.a
2.多项式+3x﹣2中,下列说法错误的是( )
A.这是一个二次三项式 B.二次项系数是1
C.一次项系数是3 D.常数项是2
3.下列各组两项中,是同类项的是( )
A.xy与﹣xy B.与 C.﹣2xy与﹣3ab D.3x2y与3xy2
4.下列计算正确的是( )
A.3a+4b=7ab B.7a-3a=4 C.3a+a=3a2 D.3a2b-4a2b=-a2b
5.绵阳到某地相距n千米,提速前火车从绵阳到某地要t小时,提速后行车时间减少了0.5小时,提速后火车的速度比原来速度快了( )
A. B. C.﹣ D.﹣
6.为庆祝战胜利70周年,我市某楼盘让利于民,决定将原价为a元/米2的商品房价降价10%销售,降价后的销售价为( )
A.a-10% B.a 10% C.a(1-10%) D.a(1+10%)
7.已知长方形的周长是45cm,一边长是acm,则这个长方形的面积是( )
A.cm2 B.a()cm2 C.cm2 D.()cm2
8.当x=1时,代数式的值是7,则当x =-1时,这个代数式的值是( )
A.7 B.3 C.1 D.-7
9.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,….
按照上述规律,第2015个单项式是( )
(A)2015x2015 (B)4029x2014 (C)4029x2015 (D)4031x2015
10.下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,...,按此规律排列,则第⑦个图形中小圆圈的个数为( )
A.21 B.24 C.27 D.30
二、填空题(每小题3分,共24分)
11.计算: .
12.单项式的系数是___________,次数是____________.
13.若单项式 与是同类项,则的值是 .
14.多项式按x的降幂排列为 .
15.甲、乙二人一起加工零件.甲平均每小时加工a个零件,加工2小时;乙平均每小时加工b个零件,加工3小时.甲、乙二人共加工零件 个.
16.如果手机通话每分钟收费元,那么通话分钟,收费 元。
17.一个多项式加上3+x一2x2。得到x2—1,则这个多项式是 .
18.如图是由火柴棒搭成的几何图案,则第n个图案中有 根火柴棒.(用含n的代数式表示)
三、计算题(第19、20小题各5分,21、22小题各6分,共22分。)
19.(2a2-1+2a)-3(a-1+a2) 20.7(m3+m2-m-1)-3(m3+m)
21.先化简后求值: 其中,
22. 小卢做一道题:“已知两个多项式A,B,计算A-B”.小卢误将A-B看作A+B,求得结果是9x2-2x+7.若B=x2+3x-2,请你帮助小卢求出A-B的正确答案.
四、解答题(每小题8分,共24分。)
23.某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.
(1)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;
(2)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?
24.某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) 水价(元/吨)
第一级 20吨以下(含20吨) 1.6
第二级 20吨﹣30吨(含30吨) 2.4
第三级 30吨以上 3.2
例:某用户的月用水量为32吨,按三级计量应缴交水费为:1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴交的水费为 元;
(2)如果乙用户缴交的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴交水费多少元?(用含a的代数式表示,并化简)
25.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的90%付款.现某客户要到该服装厂购买西装20套,领带条().
(1)若该客户按方案①购买,需付款 元(用含的代数式表示);
若该客户按方案②购买,需付款 元(用含的代数式表示).
(2)请你通过计算帮该顾客设计较为合算购买方案?
第二章整式的加减
《导学测评》参考答案
2.1 整式第1课时
1、(1)2a-5;(2)52%x,48%x;(3)(x+2x+4x);(4)(4a-25);(5)10a+b;
2、(1)4.8m元;(2)r2h;(3)a2-b2。 3、(1)C;(2)B.
2.1 整式第2课时
1、不唯一,如-2x4等;2、答案不唯一,合理就行.如:一斤鸡蛋5元钱,x斤鸡蛋的总售价是5x元. 3、,4。4、0.9a;5、D;6、D;7、(2)、(3)、(4)、(6);8、系数分别为 、2π、1、-1;次数分别为3、1、3、1。
2.1 整式第3课时
1、C、D;2、3,3,- ,- ,1;3、4;4、3,6,10,。
5、11m+1.6、5n+1。
2.2 整式的加减第1课时
1、(1)否,(2)否,(3)是,(4)是,(5)否;
2、(1)3x与-2x,-2y与3y,-5与1;(2)3x2y与-yx2,xy2与-2xy2;
3、k=2;4、m=1,n=4. 5、3. 6、(1);(2);(3)当<时,丙应缴交水费元;当<时,丙应缴交水费元;当>30时,丙应缴交水费元.
2.2 整式的加减第2课时
1、(1)2x2+3x2=5x2;(2)不可以合并;(3)7x2-3x2=4 x2;(4)对。
2、(1) ;(2)0;(3) ;(4)。
3、原式=-ab=0.001. 4、原式===19. 5、C.
2.2 整式的加减第3课时
1、C; 2、B; 3、C。 4、-1; 5、a+5; 6、(1)-x+2y;(2)-2x2-y3; 7、(1)原式=3x2-16x+3=78;(2)原式=-2x2+2x-y=2;
2.2 整式的加减第4课时
1、 ;2、2a2+b2;3、80m-40n;4、(1)7a2-3ab; (2)-3x2y+2xy;5、原式=4x3+8;6、(1) 2x3+x2+3x+2;(2)-3x3-4x2-2x-3;7、10b+a;9a-9b.
2.2 整式的加减复习课
1、D;2、3,4,-2a3b4;3、 ,6;4、-x2y+2xy2; 5、(1) (2)x+y;(3)
(4)5x2-3x-3; 6、x2-6xy+7y2 ;7、(1)原式=18x2y-6xy2=(2)原式=-3x+y2= 8、(1)(6x+2y+18);(2)45m2 ,3600元。
第二章整式的加减参考答案
一、选择题(每小题3分,共30分)
A.D.A.D.C.C.B.B.C.B.
二、填空题(每小题3分,共24分)
11.
12.系数是,次数是4.
13.5.
14.
15.(2a+3b)
16.am
17.3x2一x一4.
18.2n(n+1).
三、计算题(第19、20小题各5分,21、22小题各6分,共22分。)
19.原式=
20、原式=
21.-3x+y2,
22.7 x2-8x+11
四、解答题(每小题8分,共24分。)
23.(1)甲:①当0<ⅹ≤3时 10元;②当ⅹ>3时 10+1.2(ⅹ-3)
乙:①当0<ⅹ≤3时 8元 ②当ⅹ>3时 8+1.8(ⅹ-3)
(2)当乘坐的路程为13千米多一点,即ⅹ=14时 甲的费用23.2元,乙的费用27.8元,应乘甲种车.
24.19.2;23;当0<a≤20时1.6a、当20<a≤30时2.4a-16、当a>30时3.2a-40.
(2)设乙月用水量为x吨,根据题意得:
1.6×20+(x﹣20)×2.4=39.2,
答:乙月用水量23吨;
(3)当0<a≤20时,丙应缴交水费=1.6a(元);
当20<a≤30时,丙应缴交水费=1.6×20+2.4×(a﹣20)=2.4a﹣16(元);
当a>30时,丙应缴交水费=1.6×20+2.4×10+3.2(a﹣30)=3.2a﹣40(元).
25.(1)40x+3200;36x+3600;
(2)若x=100时,两种方案花费一样多;若x>100时,应选方案二;若x<100时,应选方案一。
【学法指导】
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
列式时要注意:
(1)数与字母相乘或字母与字母相乘,可省略乘号.
(2)数与字母相乘,数写在字母前面.
(3)除法运算要用分数线,如1÷a写成.
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
用整式表示实际问题中的数量关系和变化规律,可以从特殊值入手,借助表格等分析,由特殊到一般,由个体到整体地观察、分析问题,发现规律,并用含有字母的式子表示一般的结论,这体现了抽象的数学思想.
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来,更适合于一般规律的表达.
【预习、备课的质疑】
注意:
(1)单项式表示数与字母相乘时,通常把数字写在前面。
(2)当系数为1或-1时,这个“1”省略不写.
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【思考】多项式的每一项都包括它前面的符号吗?
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】多项式与单项式的区别与联系:
(1)多项式的次数不是所有项的次数之和;
(2)多项式的每一项都包括它前面的符号。
(3)多项式中含有运算符号“+”号或“-”号。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
①两个相同:字母相同;相同字母的指数相等。
②两个无关:与系数无关;与字母顺序无关。
③所有的常数项都是同类项。
④两个项虽然所含字母相同,但相同字母的指数不全相同就不是同类项。
【学法指导】
通常我们把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列,如:-4x2+5x+5或5+5x-4x2。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】:
合并同类项,法则不能忘,只求系数和,字母指数不变样。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
①多项式中只有同类项才能合并,不是同类项不能合并;②系数相加,字母部分不变;③确定好每一项系数的符号。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【学法指导】
去括号规律可以简单记为“-”变“+”不变,要变全都变。去括号时,要将括号连同它前面的符号一起去掉;当括号前带有数字因数时,这个数字要乘以括号内的每一项,切勿漏乘某些项.
一般地,先去小括号,再去中括号。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
【学法指导】
整式的加减其实就是合并同类项。在合并同类项时,当括号前是“-”,去括号时,括号里各项要变号。特别要注意书写格式
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【预习、备课的质疑】
【学法指导】
在学习过程中,要回顾自己犯过哪些错误,反思犯错的原因,总结一下和同学们交流。
……………………………………………………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………………………………………………
【教(学)反思】
……………………………………………………………………………………………………………………………………………………………………………………………………………………
PAGE
30
