17.1 勾股定理的应用(1) 导学案(无答案)2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 17.1 勾股定理的应用(1) 导学案(无答案)2023-2024学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 00:00:00 | ||
图片预览



文档简介
课 题 勾股定理的应用
在勾股定理应用过程中,一是找出或构造直角三角形,二是适当借助方程思想.
最短路径问题:将立体图形适当地展开成平面图形后,利用两点之间线段最短的原理,用勾股定理计算,并比较得出最短路径长度.
考点一 梯子滑动问题
要点归纳 梯子滑动问题的核心在于直角三角形结构中斜边始终不变,只要找到滑动前后两种状态中不变的量, 我们就可以建立方程进行求解.
【例1】一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )
A. 9分米 B. 15分米 C. 5分米 D. 8分米
【变1】如图,梯子AB 斜靠在墙面上, AC⊥BC, AC=BC, 当梯子的顶端A沿AC方向下滑x时, 梯足B沿CB 方向滑动y米,则x与y的大小关系是( )
A. x=y B. x>y C. x考点二 折叠问题
要点归纳 折叠问题的关键在于将本没有关系的两条线段通过折叠,变成可以构成直角三角形的三条线段,这当中一定会出现三角形的某两条边之和等于原来的某条线段,这样一个未知数就可以表示两条线段,再借助勾股定理建立方程即可求解.
【例2】已知,如图所示,折叠长方形的一边AD,使点D落在 BC边的点 F 处,如果 求 EC的长.
【变2】如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C点与A点重合,则EB的长是( )
A. 3 B. 4 C. D. 5
考点三 触礁台风问题
要点归纳 触礁台风类问题的关键在于判断定点到动点所在直线距离最小值时,是否超过临界值.而点到直线的距离,我们就需要借助直角三角形,通过勾股定理才能算得.
【例 3】台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市 A 正南256千米的B 处有一台风中心,其中心最大风力为 12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向 C 移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
(1)该城市是否会受到这次台风的影响 为什么
(2)若受到台风影响,那么台风影响该城市的持续时间有多长
(3)该城市受到台风影响的最大风力为几级
【变3】如图所示,由于过度采伐森林,我国部分地区频频遭受沙尘暴的侵袭.近日,A 城气象局测得沙尘暴中心在A 城正西方向240km的点 B 处,以12km/h的速度向北偏东( 方向移动,距沙尘暴中心 150km的范围均为受影响区域.
(1)A 城是否会受到这次沙尘暴的影响 为什么
(2)若A 城受到这次沙尘暴影响,则遭受影响的时间有多长
考点四 竖杆倾斜问题
要点归纳 我们在处理竖杆倾斜这类问题的时候,确定好高度以及最长边状态,及杆在立体图形中最大可允许的放置状态,这样就可以抽取直角三角形模型出来,利用勾股定理进行求解.
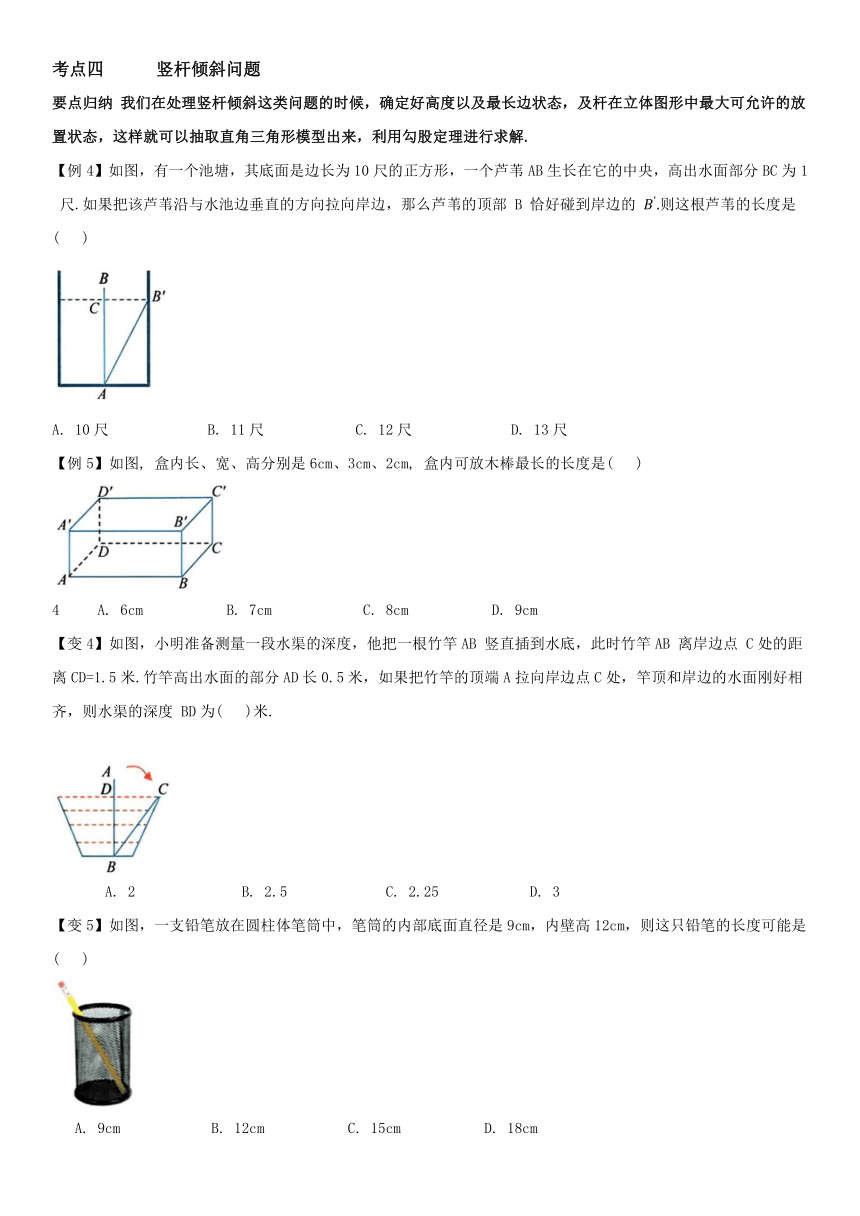
【例4】如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1 尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 B 恰好碰到岸边的 则这根芦苇的长度是
( )
10尺 B. 11尺 C. 12尺 D. 13尺
【例5】如图, 盒内长、宽、高分别是6cm、3cm、2cm, 盒内可放木棒最长的长度是( )
4 A. 6cm B. 7cm C. 8cm D. 9cm
【变4】如图,小明准备测量一段水渠的深度,他把一根竹竿AB 竖直插到水底,此时竹竿AB 离岸边点 C处的距离CD=1.5米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度 BD为( )米.
A. 2 B. 2.5 C. 2.25 D. 3
【变5】如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是
( )
A. 9cm B. 12cm C. 15cm D. 18cm
考点五 利用勾股定理解决立体图形中的最短路径问题
易错分析 长方体表面最短路径问题一般都是有三种情况,长,宽,高三个数据,任取两个求和作为一条直角边,再与另一条边结合求解.做这类题的时候需要有一定的空间想象能力,避免出现漏解的情况.
【例6】如图所示,长方体的长、宽、高分别是 8cm、4cm、5cm,一只蚂蚁沿着长方体的表面从点 A 爬到点B,求蚂蚁爬行的最短路径长.
【变6】如图所示,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点 A 开始经过4个侧面缠绕一圈到达点 B,那么所用细线最短需要 cm.
【例7】如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5 厘米的A 处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5 厘米,求小虫爬到蜜糖A处的最短距离.
【变7】如图所示,一只蚂蚁从点 A 沿圆柱表面爬到点 B,圆柱的高为8cm,圆柱的底面半径为 求最短的路线长.
【变8】如图,圆柱形玻璃杯高为 14cm,底面周长为32cm,在杯内壁离杯底5cm的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 3cm与蜂蜜相对的点 A 处,则蚂蚁从外壁 A 处到内壁B 处的最短距离为 cm(杯壁厚度不计).
考点六 勾股定理在网格中的应用
要点归纳 正方形网格中的每一个角都是直角,所以在正方形网格中的计算都可以归结为求任意两个格点之间的长度问题,一般情况下都是应用勾股定理来进行计算,关键是确定每一条边所在的直角三角形.
【例8】如图所示,在一个4×4的正方形网格中,阴影部分的面积与正方形ABCD 的面积之比为( )
A. 3:4 B. 9:16 C. 5:8 D. 1:2
【变 9】如图所示的正方形网格中,每个小正方形的边长为1,则在网格上的 中,边长为无理数的边有 条.
【变10】如图所示是由4个边长为1的正方形构成的“田字格”只用没有刻度的直尺在这个“田字格”中最多可以作出 条以格点为端点、长度为 的线段.
1. 在一次课外社会实践中,王强想知道学校旗杆的高,他发现旗杆上的绳子垂到地面上还多 1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为( )
A. 13m B. 12m C. 4m D. 10m 7m
2. 如图,有一羽毛球场地是长方形,如果AB=8米,AD=6米,若你要从A走到C, 至少走( )
A. 14米 B. 12米 C. 10米 D. 9米
3. 如图,一棵大树被大风刮断后,折断处离地面8m,树的顶端离树根6m,则这棵树在折断之前的高度是( )
A. 18m B. 10m C. 14m D. 24m
如图, 一根长 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角( 为 当木棒A 端沿墙下滑至点 A'时,B 端沿地面向右滑行至点 B', 若 则 的长为( )
D. 2
如图所示的是一扇高为2m,宽为1.5m的长方形门框,小明有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的木板最大的宽度为( )
1.5m B. 2m C. 2.5m D. 3m
6. 如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B 是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到 B 点的最短路程是( )
C. 20 D. 25
7. 如图所示,将长方形ABCD 沿着直线BD折叠,使点 C 落在点 C', BC'交 AD 于点 E, 则 DE 的长为多少
如图,一个长方体盒子紧贴地面,一只蚂蚁由A出发,在盒子表面上爬到点 G, 已知 求这只蚂蚁爬行的最短路程.
如图, 有一公路AB和一铁路 CD在点 A 处交汇,且. ,在公路的点 P 处有一所学校(学校看作点 P,点 P 与公路AB的距离忽略不计), 米,火车行驶时,火车周围200米以内会受到噪音的影响,现有一列动车在铁路 CD上沿AD 方向行驶,该动车车身长200米,动车的速度为180千米/时,那么在该动车行驶过程中.
(1)学校P 是否会受到噪声的影响 说明理由;
(2)如果受噪声影响,那么学校P受影响的时间为多少秒
如图,东西方向上有 A,C两地相距10千米,甲以16千米/时的速度从A地出发向正东方向前进,乙以12千米/时的速度从C地出发向正南方向前进,那么最快经过( )小时,甲、乙两人相距6千米.
A. B. C. 1.5
2. 如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底 1cm的点B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁 B 处的最短距离为 .
3.如图,是一个长、宽、高分别为4cm、2cm、8cm的无盖长方体盒子,现有一只蚂蚁从点 A 处沿盒子的内壁爬到点 B,则爬行的最短距离为( )
D. 10cm
4. 如图,MN是一条东西朝向的笔直的公路,C 是位于该公路上的一个检测点,一辆长为9m的小货车 BD行驶在该公路上,小王位于点A处观察小货车,某时刻他发现车头D、车尾 B 及检测点C 分别距离他10m、
(1)过点A向 MN引垂线,垂足为E,请利用勾股定理分别找出线段AE与DE、AE与BE之间所满足的数量关系;
(2)在上一问的提示下,继续完成下列问题:
①求线段 DE的长度;
②该小货车的车头D距离检测点 C 还有多少m
5. “交通管理条例第三十五条”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方50米处,过了6秒后,测得小汽车与车速检测仪间距离为130米,这辆小汽车超速了吗
在勾股定理应用过程中,一是找出或构造直角三角形,二是适当借助方程思想.
最短路径问题:将立体图形适当地展开成平面图形后,利用两点之间线段最短的原理,用勾股定理计算,并比较得出最短路径长度.
考点一 梯子滑动问题
要点归纳 梯子滑动问题的核心在于直角三角形结构中斜边始终不变,只要找到滑动前后两种状态中不变的量, 我们就可以建立方程进行求解.
【例1】一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )
A. 9分米 B. 15分米 C. 5分米 D. 8分米
【变1】如图,梯子AB 斜靠在墙面上, AC⊥BC, AC=BC, 当梯子的顶端A沿AC方向下滑x时, 梯足B沿CB 方向滑动y米,则x与y的大小关系是( )
A. x=y B. x>y C. x
要点归纳 折叠问题的关键在于将本没有关系的两条线段通过折叠,变成可以构成直角三角形的三条线段,这当中一定会出现三角形的某两条边之和等于原来的某条线段,这样一个未知数就可以表示两条线段,再借助勾股定理建立方程即可求解.
【例2】已知,如图所示,折叠长方形的一边AD,使点D落在 BC边的点 F 处,如果 求 EC的长.
【变2】如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C点与A点重合,则EB的长是( )
A. 3 B. 4 C. D. 5
考点三 触礁台风问题
要点归纳 触礁台风类问题的关键在于判断定点到动点所在直线距离最小值时,是否超过临界值.而点到直线的距离,我们就需要借助直角三角形,通过勾股定理才能算得.
【例 3】台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市 A 正南256千米的B 处有一台风中心,其中心最大风力为 12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向 C 移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
(1)该城市是否会受到这次台风的影响 为什么
(2)若受到台风影响,那么台风影响该城市的持续时间有多长
(3)该城市受到台风影响的最大风力为几级
【变3】如图所示,由于过度采伐森林,我国部分地区频频遭受沙尘暴的侵袭.近日,A 城气象局测得沙尘暴中心在A 城正西方向240km的点 B 处,以12km/h的速度向北偏东( 方向移动,距沙尘暴中心 150km的范围均为受影响区域.
(1)A 城是否会受到这次沙尘暴的影响 为什么
(2)若A 城受到这次沙尘暴影响,则遭受影响的时间有多长
考点四 竖杆倾斜问题
要点归纳 我们在处理竖杆倾斜这类问题的时候,确定好高度以及最长边状态,及杆在立体图形中最大可允许的放置状态,这样就可以抽取直角三角形模型出来,利用勾股定理进行求解.
【例4】如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1 尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 B 恰好碰到岸边的 则这根芦苇的长度是
( )
10尺 B. 11尺 C. 12尺 D. 13尺
【例5】如图, 盒内长、宽、高分别是6cm、3cm、2cm, 盒内可放木棒最长的长度是( )
4 A. 6cm B. 7cm C. 8cm D. 9cm
【变4】如图,小明准备测量一段水渠的深度,他把一根竹竿AB 竖直插到水底,此时竹竿AB 离岸边点 C处的距离CD=1.5米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度 BD为( )米.
A. 2 B. 2.5 C. 2.25 D. 3
【变5】如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是
( )
A. 9cm B. 12cm C. 15cm D. 18cm
考点五 利用勾股定理解决立体图形中的最短路径问题
易错分析 长方体表面最短路径问题一般都是有三种情况,长,宽,高三个数据,任取两个求和作为一条直角边,再与另一条边结合求解.做这类题的时候需要有一定的空间想象能力,避免出现漏解的情况.
【例6】如图所示,长方体的长、宽、高分别是 8cm、4cm、5cm,一只蚂蚁沿着长方体的表面从点 A 爬到点B,求蚂蚁爬行的最短路径长.
【变6】如图所示,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点 A 开始经过4个侧面缠绕一圈到达点 B,那么所用细线最短需要 cm.
【例7】如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5 厘米的A 处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5 厘米,求小虫爬到蜜糖A处的最短距离.
【变7】如图所示,一只蚂蚁从点 A 沿圆柱表面爬到点 B,圆柱的高为8cm,圆柱的底面半径为 求最短的路线长.
【变8】如图,圆柱形玻璃杯高为 14cm,底面周长为32cm,在杯内壁离杯底5cm的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 3cm与蜂蜜相对的点 A 处,则蚂蚁从外壁 A 处到内壁B 处的最短距离为 cm(杯壁厚度不计).
考点六 勾股定理在网格中的应用
要点归纳 正方形网格中的每一个角都是直角,所以在正方形网格中的计算都可以归结为求任意两个格点之间的长度问题,一般情况下都是应用勾股定理来进行计算,关键是确定每一条边所在的直角三角形.
【例8】如图所示,在一个4×4的正方形网格中,阴影部分的面积与正方形ABCD 的面积之比为( )
A. 3:4 B. 9:16 C. 5:8 D. 1:2
【变 9】如图所示的正方形网格中,每个小正方形的边长为1,则在网格上的 中,边长为无理数的边有 条.
【变10】如图所示是由4个边长为1的正方形构成的“田字格”只用没有刻度的直尺在这个“田字格”中最多可以作出 条以格点为端点、长度为 的线段.
1. 在一次课外社会实践中,王强想知道学校旗杆的高,他发现旗杆上的绳子垂到地面上还多 1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为( )
A. 13m B. 12m C. 4m D. 10m 7m
2. 如图,有一羽毛球场地是长方形,如果AB=8米,AD=6米,若你要从A走到C, 至少走( )
A. 14米 B. 12米 C. 10米 D. 9米
3. 如图,一棵大树被大风刮断后,折断处离地面8m,树的顶端离树根6m,则这棵树在折断之前的高度是( )
A. 18m B. 10m C. 14m D. 24m
如图, 一根长 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角( 为 当木棒A 端沿墙下滑至点 A'时,B 端沿地面向右滑行至点 B', 若 则 的长为( )
D. 2
如图所示的是一扇高为2m,宽为1.5m的长方形门框,小明有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的木板最大的宽度为( )
1.5m B. 2m C. 2.5m D. 3m
6. 如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B 是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到 B 点的最短路程是( )
C. 20 D. 25
7. 如图所示,将长方形ABCD 沿着直线BD折叠,使点 C 落在点 C', BC'交 AD 于点 E, 则 DE 的长为多少
如图,一个长方体盒子紧贴地面,一只蚂蚁由A出发,在盒子表面上爬到点 G, 已知 求这只蚂蚁爬行的最短路程.
如图, 有一公路AB和一铁路 CD在点 A 处交汇,且. ,在公路的点 P 处有一所学校(学校看作点 P,点 P 与公路AB的距离忽略不计), 米,火车行驶时,火车周围200米以内会受到噪音的影响,现有一列动车在铁路 CD上沿AD 方向行驶,该动车车身长200米,动车的速度为180千米/时,那么在该动车行驶过程中.
(1)学校P 是否会受到噪声的影响 说明理由;
(2)如果受噪声影响,那么学校P受影响的时间为多少秒
如图,东西方向上有 A,C两地相距10千米,甲以16千米/时的速度从A地出发向正东方向前进,乙以12千米/时的速度从C地出发向正南方向前进,那么最快经过( )小时,甲、乙两人相距6千米.
A. B. C. 1.5
2. 如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底 1cm的点B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁 B 处的最短距离为 .
3.如图,是一个长、宽、高分别为4cm、2cm、8cm的无盖长方体盒子,现有一只蚂蚁从点 A 处沿盒子的内壁爬到点 B,则爬行的最短距离为( )
D. 10cm
4. 如图,MN是一条东西朝向的笔直的公路,C 是位于该公路上的一个检测点,一辆长为9m的小货车 BD行驶在该公路上,小王位于点A处观察小货车,某时刻他发现车头D、车尾 B 及检测点C 分别距离他10m、
(1)过点A向 MN引垂线,垂足为E,请利用勾股定理分别找出线段AE与DE、AE与BE之间所满足的数量关系;
(2)在上一问的提示下,继续完成下列问题:
①求线段 DE的长度;
②该小货车的车头D距离检测点 C 还有多少m
5. “交通管理条例第三十五条”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方50米处,过了6秒后,测得小汽车与车速检测仪间距离为130米,这辆小汽车超速了吗
